Кривая дракона

Кривая дракона

Д.М. Златопольский

В ряде публикаций газеты “Информатика”, посвященных компьютерной графике [1—3], были представлены программы, рисующие на экране красивые фигуры, орнаменты и даже изображения растений. Как правило, в них использовалась рекурсия [4—5]. Однако красивые линии с повторяющимся рисунком можно получить и с помощью простых итеративных алгоритмов. Пример такой линии — кривая, изображенная на рис. 1. Прежде чем описывать методику ее построения, рассмотрим кривые, которые можно получить следующим образом. Возьмем длинную полоску бумаги и сложим ее пополам, а затем развернем на 900. Если смотреть на полоску сбоку, то получится ломаная линия из двух перпендикулярных участков: см. рис. 2а. Теперь сложим полоску пополам дважды и также дважды развернем на 900 так, как это показано на рис. 2б. Получим ломаную линию уже из четырех отрезков, причем угол между смежными отрезками составляет 900 . Наконец, если сложение и разворачивание полоски осуществить три раза, то в результате получится фигура, представленная на рис. 2в. Продолжая этот процесс, можно получить кривую, аналогичную той, которая представлена на рис. 1 (прямые углы у кривой на этом рисунке скруглены). Эту причудливую кривую называют кривой дракона. Способ построения подсказывает, что она не имеет самопересечений.

dragon1.jpg (7726 bytes)

Рис. 1

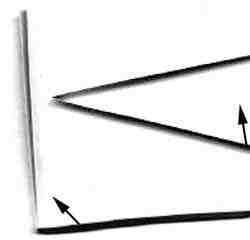
dragon2.jpg (2871 bytes)

dragon3.jpg (2280 bytes)

dragon4.jpg (3594 bytes)

Рис 2

Приступим к разработке программы построения кривой дракона. Начнем с того, что будем наблюдать ход ломаных линий на рис. 2в, начиная с отрезка 1, и на каждом углу следить, поворачивается отрезок на 900 вправо (по часовой стрелке) или влево (против часовой стрелки). Присвоим код 1 повороту влево и код 3 повороту вправо и обозначим код для отрезка с номером i через K(i). Из рис. 2в видно, что

K(1)=1; K(2)=1; K(3)=3; K(4)=1; K(5)=1; K(6)=3; K(7)=3.

Задача заключается в том, чтобы найти правило выбора направления поворота (влево или вправо) в конце отрезка с номером i (i=1, 2, ...).

Если рассмотреть ломаные, аналогичные представленной на рис. 2в, но состоящие из 16, 32 и т.д. отрезков, и проанализировать зависимость направления поворота от номера отрезка, то можно установить, что значение K(i) определяется следующим образом:

K(i)=K(i div 2), если i четное;

K(i)=i mod 4, если i нечетное,

где div — целочисленное деление, а mod — операция определения остатка.

Определение значений K(i) может быть проведено с помощью рекурсивной функции, на школьном алгоритмическом языке [4, 6] имеющей вид:

алг цел K(арг цел i)

нач
если mod(i, 2)=0 то
знач:=K(div(i, 2)) | рекурсивный вызов функции
иначе
знач:=mod(i, 4)
все

| знач - значение функции K

кон

Построение очередного отрезка ломаной удобно выполнять с использованием команды, которая на школьном алгоритмическом языке называется вектор. Эта команда проводит линию из текущей позиции в точку, заданную приращением ее координат. В Паскале и Си аналогичную роль выполняет команда linerel, а в Бейсике модификация команды LINE: LINE -STEP (dx,dy), где dx,dy — приращения координат.

В процедуре Step, выполняющей построение, рассматриваются 4 варианта направления перемещения (2 направления по горизонтали и 2 по вертикали). Направление задается величиной angle. При перемещении вертикально вверх значение этой величины равно 0, горизонтально влево –90, вертикально вниз –180 и горизонтально вправо –270 (т.е. отсчет производится против часовой стрелки от направления вертикально вверх). Длина отрезка ломаной обозначена len.

алг Step(арг цел angle)

нач
   выбор
     при angle=0 : вектор(0, -len)
     при angle=180 : вектор(0, len)
     при angle=270 : вектор(len, 0)
     при angle=90 : вектор(-len, 0)
   все

кон

Определим закономерности изменения значения угла angle в ходе построения ломаной. Можно утверждать, что в конце каждого отрезка с номером i мы должны повернуть на K(i)*900 влево, поскольку поворот на 900 по часовой стрелке эквивалентен повороту на 2700 влево против часовой стрелки. Тогда с учетом принятой системы отсчета угла angle его очередное (после поворота) значение связано с предыдущим значением зависимостью:

angle:=mod ((angle+K(i)*90), 360), (1)

где mod — операция определения остатка, а K(i) — код направления поворота (см. выше).

С использованием функции K и процедуры Step, а также формулы (1) основная часть программы может быть оформлена в виде:

цел len |величину len описываем как глобальную

алг Ломаная

   нц для i от 1 до n-1
     angle:=mod ((angle+K(i)*90), 360)
     нц 5000 раз |пауза
     кц
     Step(angle) |рисуем остальные отрезки линии
   кц

кон

Примечания.

1. Принятые значения координат начальной точки ломаной, а также длины отрезков обеспечивают размещение на экране всей линии из 418 отрезков.

2. “Пустой” цикл в программе создает небольшую паузу между вычерчиванием отрезков.

Поскольку функция K(i) рекурсивная, то полностью избежать рекурсии, о чем говорилось в начале статьи, не удалось. Между тем в данном случае рекурсия связана с многократным повторением одних и тех же операций. Действительно, для нахождения K(8) надо определить K(4), K(2), K(1), а все эти величины уже были найдены и использованы ранее. Попробуем поступить так: будем хранить значения K в массиве arrK[1:n]. Для нечетных i значения K находятся непосредственно по формуле K=i mod 4. Поэтому сначала заполняем нечетные элементы указанного массива, после чего в цикле по четным i от 2 до последнего значения, не превышающего n, находим K[i] по соотношению: K[i]=K[i div 2]. Как обычно, повышение быстродействия потребовало дополнительных затрат памяти. Мы не будем приводить программную реализацию такого подхода к определению K, предоставив это заинтересованному читателю.

Как уже говорилось, замечательным свойством полученной линии является то, что в ней отсутствуют самопересечения (помните о складываемой полоске бумаги?). Чтобы наглядно продемонстрировать указанную особенность, можно скруглить все углы или, точнее, заменить их небольшими отрезками прямых линий (т.е. при этом во всех вершинах ломаной будем иметь углы 1350 вместо 900). На рис. 1 как раз и представлена такая линия.

Для ее построения уточним приведенную программу. Основные изменения должны быть внесены в процедуру Step. Включим в нее также рисование “закругления”, предшествующего очередному отрезку. Очевидно, что для вычерчивания этого “скругления” необходимо знать предшествующее направление перемещения. Информацию о нем будем хранить в переменной old_angle. Естественно, что длина вычерчиваемого отрезка в данном случае уменьшается до len-2*a, где a — длина катета “закругления”. С учетом этого процедура Step оформляется следующим образом:

dragon5.jpg (6655 bytes)

алг Step(арг цел angle, арг рез цел old_angle)

нач

выбор
при angle=0:
если old_angle=90
то
вектор(-a, -a)
иначе
вектор(a, -a)
все

вектор(0, -(len-2*a))
при angle=180:
если old_angle=90
то
вектор(-a, a)
иначе
вектор(a, a)
все

вектор(0, len-2*a)
при angle=270:
если old_angle=0
   то
    вектор(a, -a)
   иначе
    вектор(a, a)
все

вектор(len-2*a, 0)
при angle=90:
если old_angle=0
   то
   вектор(-a, -a)
иначе
   вектор(-a, a)
все

вектор(-(len-2*a), 0)
все
old_angle:=angle

кон

Основная часть программы меняется незначительно:

цел len, a |о величине a - см. процедуру Step

алг Кривая дракона

нач цел n, angle, old_angle, i
видео(17)
поз(190+a, 276)
len:=20
a:=div(len, 5)
angle:=270
вектор(len-a, 0)
old_angle:=270
n:=418

нц для i от 1 до n-1
   angle:=mod ((angle+K(i)*90), 360)
     нц 10000 раз |пауза
     кц
   Step(angle,old_angle)
кц

кон

Язык Паскаль

Uses graph,crt;
Const
len=20;{Длина отрезков ломаной}
a=len div 5;{Длина катета "закругления"}
path=''; {Файлы *.BGI находятся в текущем каталоге}
var
d,r,n:integer;
i,angle,old_angle:word;
{Функция, определяющая значение кода направления поворота в конце
отрезка с номером i}

function K(i:word):byte;
begin if Odd(i) then K:=i mod 4 else K:=K(i div 2) end;
{Процедура рисования отрезка ломаной и предшествующего ему
"закругления"}

Procedure Step(angle:word; var old_angle:word);

   begin
    {Рассматриваем 4 варианта направления перемещения. Вычерчиваем
     "закругление" и очередной отрезок }

   Case angle of
    0: begin
        if old_angle=90 then LINEREL(-a,-a) else LINEREL(a,-a);
        LINEREL(0,-(len-2*a))
       end;

180: begin
        if old_angle=90 then LINEREL(-a,a) else LINEREL(a,a);
        LINEREL(0,len-2*a)
       end;

90: begin
        if old_angle=0 then LINEREL(-a,-a) else LINEREL(-a,a);
        LINEREL(-(len-2*a),0)
      end;

270: begin
        if old_angle=0 then LINEREL(a,-a) else LINEREL(a,a);
        LINEREL(len-2*a,0)
      end;
end;{Case angle}

old_angle:=angle

end;

BEGIN
d:=DETECT;{режим автоопределения типа монитора}
INITGRAPH(d, r, path); {Переход в графический режим}
MOVETO(190+a, 276); {Начальная точка ломаной}
angle:=270; {Угол наклона первого отрезка}
LINEREL(len-a,0); {Рисуем первый отрезок}
old_angle:=270;
n:=418; {Количество отрезков}
for i:=1 to n-1 do
   begin
    angle:=(angle+K(i)*90) mod 360;
    DELAY(2000);{Задеpжка}
    Step(angle, old_angle) {рисуем остальные отрезки линии}
   end;

repeat until keypressed;{Останов до нажатия любой клавиши}
END.

Язык Бейсик (вариант Quickbasic [7])

В программе на этом языке процедура рисования отрезка ломаной и предшествующего ему “закругления” имеет имя Ste, а величина длины отрезка ломаной — leng.

'Описываем используемые процедуру, функцию и величины
DECLARE FUNCTION K% (i AS INTEGER)
DECLARE SUB Ste (angle AS INTEGER, oldangle AS INTEGER)
DIM SHARED leng AS INTEGER 'Длина отрезков ломаной
DIM SHARED a AS INTEGER 'Длина катета "закругления"
DEFINT A-O
SCREEN (11) 'Пеpеход в графический режим для монитора VGA
leng = 20 'Длина отрезков ломаной
a = leng \ 5 'Длина катета "закругления"
angle = 270 'Угол наклона первого отрезка
LINE (190 + a, 276)-STEP(leng - a, 0) 'Рисуем первый отрезок
oldangle = 270
n = 418 'Количество отрезков

FOR i = 1 TO n - 1
angle = (angle + K%(i) * 90) MOD 360
FOR j = 1 TO 32000: NEXT j 'Задеpжка
CALL Ste(angle, oldangle) 'рисуем остальные отрезки линии
NEXT i

SLEEP 'Останов до нажатия любой клавиши
END

SUB Ste (angle AS INTEGER, oldangle AS INTEGER)
'Процедура рисования отрезка ломаной и предшествующего ему
'"закругления".Рассматриваем 4 варианта направления перемещения
'Вычерчиваем "закругление" и очередной отрезок

SELECT CASE angle
CASE 0
   IF oldangle = 90 THEN LINE -STEP(-a, -a)
     ELSE LINE -STEP(a, -a)
   END IF
   LINE -STEP(0, -(leng - 2 * a))
CASE 180
   IF oldangle = 90 THEN LINE -STEP(-a, a)
    ELSE LINE -STEP(a, a)
   END IF
   LINE -STEP(0, leng - 2 * a)
CASE 270
   IF oldangle = 0 THEN LINE -STEP(a, -a)
     ELSE LINE -STEP(a, a)
   END IF
   LINE -STEP((leng - 2 * a), 0)
CASE 90
   IF oldangle = 0 THEN LINE -STEP(-a, -a)
    ELSE LINE -STEP(-a, a)
   END IF
   LINE -STEP(-(leng - 2 * a), 0)
END SELECT

oldangle = angle
END SUB

FUNCTION K% (i AS INTEGER)
'Функция, определяющая значение кода направления
'поворота в конце отрезка с номером i
IF i MOD 2 = 0 THEN K% = K%(i \ 2) ELSE K% = i MOD 4
END FUNCTION

Язык Си

#include<graphics.h>
#include <conio.h>
#define len 20 /*Длина отрезков ломаной*/
#define PATH "" /*Файлы *.BGI находятся в текущем каталоге*/
int a;/*Длина катета "закругления"*/;
/*Функция, определяющая значение кода направления
поворота в конце отрезка с номером i */
int K(int i)
{if (i % 2 == 1) return i % 4; else return K(i/2);}

/*Функция рисования отрезка ломаной и предшествующего ему "закругления" */
void Step(int angle, int *old_angle)
{/*Рассматриваем 4 варианта направления перемещения.
Вычерчиваем "закругление" и очередной отрезок*/
switch (angle)
   {case 0:
      if (*old_angle==90) linerel(-a,-a); else linerel(a,-a);
      linerel(0,-(len-2*a)); break;
    case 180:
      if (*old_angle==90) linerel(-a,a); else linerel(a,a);
      linerel(0,(len-2*a)); break;
    case 90:
      if (*old_angle==0) linerel(-a,-a); else linerel(-a,a);
      linerel(-(len-2*a),0); break;
    case 270:
      if (*old_angle==0) linerel(a,-a); else linerel(a,a);
      linerel(len-2*a,0); break;
    }

*old_angle=angle;

}

void main()
{int d=DETECT,/*режим автоопределения типа монитора*/
   r,n=418/*Количество отрезков*/,i,
   angle=270,/*Угол наклона первого отрезка*/
   old_angle=270;
   a=len/5;
   initgraph(&d,&r,PATH);/*Переход в графический режим*/
   moveto(190+a, 276); /*Начальная точка ломаной*/
   linerel(len-a,0); /*Рисуем первый отрезок*/
   for (i=1; i<n; i++)
    {angle=(angle+K(i)*90) % 360;
     delay(2000);/*Задеpжка*/
     Step(angle, &old_angle);/*рисуем остальные отрезки линии*/
    }
getch();/*Останов до нажатия любой клавиши*/
}

Литература

1. Островский С.Л. Фрактальные кривые. Информатика, 1995, № 23.

2. Елки, палки и прочие фракталы. Информатика, 1998, № 19.

3. Островский С.Л., Соколинский Ю.А. Задачи по теме “Компьютерная графика”. Выпуск 1. Информатика, 1998, № 30.

4. Кушниренко А.Г., Лебедев Г.В., Сворень Р.А. Основы информатики и вычислительной техники. М.: Просвещение, 1990.

5. Златопольский Д.М. Рекурсия. Информатика, 1996, № 7—8.

6. Эпиктетов М.Г. Почему школьный алгоритмический? Информатика, 1995, № 24.

7. Зельднер Г.А. QuickBasic 4.5. М.: ABF, 1994.

Кривая дракона:послесловие

Кривая дракона, о которой рассказано в статье Д.М. Златопольского (см. с. 2, 3), впервые была описана в популярной литературе в журнале Scientific American в 1967 году. Заметка о ней появилась в колонке “Математические игры”, которую вел Мартин Гарднер. Первоначально использовалось полное название кривой – “дракон Хартера — Хейтуэя”, которое ей дал основатель компьютерной фрактальной геометрии Бенуа Мандельброт, именем которого названо знаменитое множество. В дальнейшем стали говорить просто о кривой дракона. В статье Д.М. Златопольского описан один из алгоритмов построения кривой. На наш взгляд, он несколько запутан (хотя и достаточно прост в реализации). В этой заметке мы приведем описание алгоритма построение кривой, близкое к тому, которое использовалось Мартином Гарднером.

Рис. 1

Рассмотрим горизонтальный отрезок как кривую дракона нулевого порядка. Разделим отрезок пополам и построим на нем прямой угол, как показано на рис. 1. Получим кривую дракона первого порядка. На сторонах прямого угла снова построим прямые углы (рис. 2).

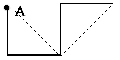
Рис. 2

При этом вершина первого угла всегда находится справа, если смотреть из точки A (начала кривой) вдоль первого отрезка кривой, а направления, в которых строятся вершины остальных углов, чередуются. На рис. 3 и 4 показаны кривые дракона третьего и четвертого порядков соответственно.

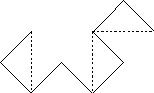
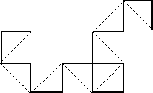
рис. 3 рис. 4

Кривая дракона просто и изящно описывается в так называемой L-системе (предложенной Линденмауэром). Об этой системе, которую также называют черепашьей, вы можете прочитать в заметке “Елки, палки и прочие фракталы” (см. № 19/98). В L-системе дракон Хартера — Хейтуэя описывается с помощью одной “аксиомы” FX и двух “теорем”: +FX--FY+ и -FX++FY-. Угол поворота (который, напомним, используется в командах + и -) равен 45o.

Кривая дракона – один из популярнейших объектов, который встречается практически во всех курсах фрактальной геометрии. Описание алгоритма построения кривой и множество другой интересной информации (в частности, ссылок на другие источники) находится, например, на http://astsun.astro.virginia.edu/~eww6n/math/DragonCurve.html . Краткое, но очень понятное описание можно найти на http://www.math.okstate.edu/mathdept/dynamics/dragon.html . Имеется также множество русскоязычных источников, например, http://home.ural.ru/~shabun/fractals/fractals.htm .