
В компьютерной графике для обработки черно-белых изображений часто используется преобразование изображения в строку из десятичных чисел.
Предположим для простоты, что изображение имеет форму квадрата. Изображение или его часть (квадрат меньшего размера) последовательно делится на 4 равных квадрата. Если все точки в квадрате одного цвета (черного или белого), то процесс деления этой части изображения заканчивается. Квадраты, содержащие как черные, так и белые точки, опять делятся. Процесс продолжается до тех пор, пока каждый из квадратов не будет содержать точки только одного цвета.
Например, если использовать 0 для обозначения точек белого цвета и 1 для обозначения точек черного цвета, то изображение на рис. 1а будет записано следующей матрицей из нулей и единиц (рис. 1б). Матрица будет разделена на квадраты, как показано на рис. 1в. Серым выделены квадраты, содержащие только черные точки.

Рис. 1а.
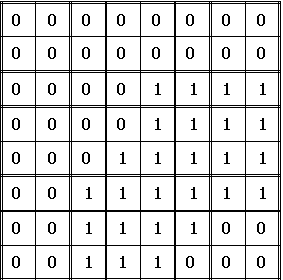
Рис. 1б.
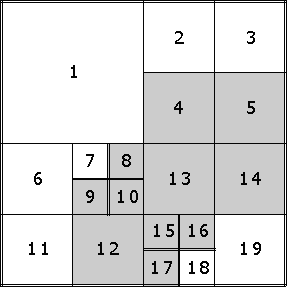
Рис. 1в.
Преобразование изображения в дерево выполняется следующим образом. Корень дерева представляет все изображение. Каждая вершина дерева описывает некий квадрат. Она может иметь 4 исходящих ребра к другим вершинам, представляющим квадраты, на которые делится исходный. Вершины без исходящих ребер соответствуют квадратам, состоящим из точек одного цвета. Например, изображению на рис. 1а с его разбивкой на квадраты соответствует дерево (рис. 2). Серые вершины обозначают квадраты, содержащие 2 цвета, а белые и черные — квадраты, состоящие из точек одного цвета (такого же, как цвет квадрата).
В дереве вершины пронумерованы в соответствии с нумерацией квадратов на рисунке. Квадраты обходятся слева направо и сверху вниз, начиная с верхнего левого угла (верхний левый, верхний правый, нижний левый, нижний правый). Каждая черная вершина дерева кодируется следующим образом: поднимаемся от вершины по ребрам к корню, записывая при этом подряд цифры от 1 до 4 в соответствии с тем, где находится текущий квадрат по отношению к вышестоящему (верхний левый — 1, верхний правый — 2, нижний левый — 3, нижний правый — 4). Получается число, записанное в системе счисления по основанию 5. Переводим его в десятичную систему счисления.
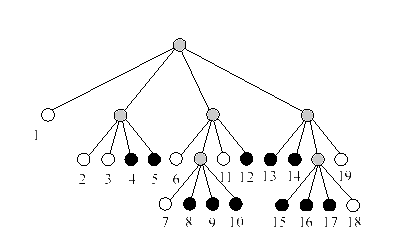
Рис. 2
Например, вершина с номером 4 имеет путь Н—Л, В—П. Получается число 32
5 (по основанию 5), или 1710 (по основанию 10). Вершина с номером 12 имеет путь Н—П, Н—Л, или 435 и 2310 соответственно. Вершина с номером 15 имеет путь В—Л, Н—Л, Н—П, или 1345=4410. Все дерево (и, соответственно, изображение) кодируется строкой чисел: 9 14 17 22 23 44 63 69 88 94 113.Требуется написать программу перевода изображения в строку чисел и обратного преобразования — строки чисел в изображение.
Входные данные
Файл содержит описание одного или нескольких изображений. Все изображения — это квадратные рисунки, длины сторон квадратов — целые числа, являющиеся степенями двойки. Входной файл начинается с целого числа n, где |n| — длина стороны квадрата (|n| < 64). Если число n больше 0, то затем следует |n| строк по |n| знаков в строке, заполненных 0 и 1. При этом 1 соответствует черному цвету. Если n меньше 0, то затем следует описание изображения в виде строки из десятичных чисел, оканчивающейся —1. Полностью черному квадрату соответствует строка из одного 0. Белый квадрат кодируется пустой строкой (ничего не вводится). Признаком конца входного файла является значение n, равное 0.
Выходные данные
Для каждого изображения из входного файла выводится его номер. В том случае, когда изображение задается с помощью 0 и 1, в выходной файл записывается его представление в виде строки десятичных чисел. Числа в строке сортируются в порядке возрастания. Для изображений, содержащих больше 12 черных областей, после каждых 12 чисел вывод начинается с новой строки. Количество черных областей выводится после строки из десятичных чисел. В том случае, когда изображение задается строкой из десятичных чисел, в выходной файл записывается его представление в виде квадрата, в котором символ ‘.’ соответствует 0, а символ ‘*’ — 1. Пример входного и выходного файлов приведен в таблице.
| Входной файл | Выходной файл |
| 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 1 0 0 0 0 1 1 1 0 0 0 |
Изображение 1 9 14 17 22 23 44 63 69 88 94 113 Общее число черных областей 11 |
| —8 9 14 17 22 23 44 63 69 88 94 113 —1 |
Изображение 2 . . . . . . . . . . . . . . . . . . . . * * * * . . . . * * * * . . . * * * * * . . * * * * * * . . * * * * . . . . * * * . . . |
| 2 0 0 0 0 |
Изображение 3 Общее число черных областей 0 |
| —4 0 —1 |
Изображение 4 * * * * * * * * * * * * * * * * |
Решение
Основная программа практически не требует пояснений.
BeginAssign(Input,'Input.txt');Reset(Input);
Assign(Output,'Output.txt');Rewrite(Output);
Readln(N);{вводим размерность изображения}
NumTest:=0;{переменная для хранения номера теста}
While N<>0 do begin
Inc(NumTest);
Writeln('Изображение',NumTest);
If N>0 Then SolveA else SolveB; {первая процедура
преобразует изображение
в виде матрицы в строку десятичных
чисел, вторая процедура выполняет
обратное преобразование}
end;
Close(Input);
Close(Output);
End.
Дальнейшее уточнение требует осознания того, каким образом в нашей задаче описывается очередной квадрат. Для описания квадрата надо знать координаты левого верхнего угла, длину стороны и тот путь по изображению, который предшествовал попаданию в этот квадрат. Путь по изображению — строка из цифр от 1 до 4. Назовем функцию обработки квадрата
RecA:Function RecA(i,j,d:integer;
var Way:string):boolean.
Функция возвращает значение
true, если квадрат черный. Введем массив для хранения результата — десятичных чисел, описывающих изображение. Назовем его Cp (Cp:Array[1..MaxCn] Of LongInt, где MaxCn — константа, равная 642). Счетчиком числа записей в Cp является значение переменной Cnt. Исходное изображение записано в массиве A (A:Array[1..MaxN,1..MaxN] of boolean, где MaxN — константа, равная 64). Значение элемента массива A[i,j], равное true, соответствует черной клетке с координатами (i,j), значение false — белой. Приведем процедуру SolveA. Procedure SolveA;Функция RecA имеет вид:
Funсtion RecA(i,j,d:integer;Way:string):boolean; If c Then Dec(Cnt,4);
{если все составляющие квадраты черные,
то и данный квадрат черный}
End;
If c Then Begin Inc(Cnt);
{квадрат черный, преобразуем путь (строку,
описывающую число в пятеричной системе
счисления) в десятичное число и
записываем
результат}
Cp[Cnt]:=<преобразовать строку символов,
Осталось уточнить функцию преобразования пути по квадрату в десятичное число. Процедуры Sort и PrintA, мы вызываем их из процедуры SolveA, они “прозрачны”.
Function Fr5To10(S:String):LongInt;Рассмотрим теперь процедуру получения матрицы, описывающей изображение, из строки десятичных чисел.
Procedure SolveB;Функция перевода числа из одной системы счисления в другую достаточно прозрачна, но для полноты картины приведем ее.
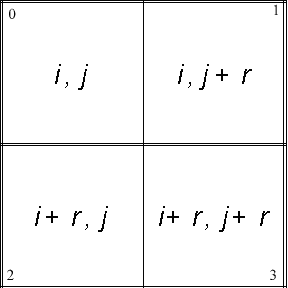 Function Fr10To5(S:LongInt):LongInt;
Function Fr10To5(S:LongInt):LongInt;С процедурой RecB чуть сложнее. Квадрат описывается координатами верхнего левого угла и длиной стороны. Кроме того, у нас есть путь, представленный пятеричным числом. Вопрос: как из очередной цифры этого числа сделать переадресацию по квадрату, т.е. перейти к одному из четырех квадратов меньшего размера? Ответив на него, мы поймем суть процедуры RecB. Поясним ситуацию рисунком. Пусть координаты левого верхнего угла квадрата задаются значениями переменных i и j, а длина стороны нового квадрата — значение r. Цифры в кружках — это значения переменной k, получаемой из очередной цифры пятеричного числа с помощью операции k:=Way Mod 5–1. В зависимости от значения переменной k с помощью операций i+r*(k Div 2) и j+r*(k Mod 2) мы переходим к левым верхним углам любого из четырех квадратов меньшего размера. Проиллюстрируем это примером.
| Номер вызова процедуры RecB | i | j | d | Way | k | r |
| 1 | 1 | 1 | 8 | 325 или 1710 | 1 | 4 |
| 2 | 1 | 5 | 4 | 3 | 2 | 2 |
| 3 | 3 | 5 | 2 | 0 | - | - |
Таким образом, черным цветом будет закрашен квадрат, отмеченный цифрой 4 на рисунке в формулировке задачи. Итак, процедура RecB.
Procedure RecB(i,j,d:Integer;Way:LongInt);