Задача "Ресторан"

С.М.Окулов

В ресторане собираются N посетителей. Посетитель с номером i, имеющий сумму денег P_i и полноту S_i, подходит к двери ресторана во время T_i. Входная дверь ресторана имеет K состояний открытости. Состояние открытости двери может изменяться на одну единицу за единицу времени: дверь открывается на единицу или остается в том же состоянии. В начальный момент времени дверь закрыта (состояние 0). Посетитель с номером i входит в ресторан только в том случае, если дверь открыта специально для него, то есть когда состояние открытости двери совпадает с его степенью полноты S_i. Если в момент прихода посетителя состояние двери не совпадает с его степенью полноты, то посетитель уходит и больше не возвращается.

Ресторан работает в течение времени T.

Требуется, правильно открывая и закрывая дверь, добиться того, чтобы за время работы ресторана в нем собрались посетители, общая сумма денег у которых максимальна.

Входные данные

В первой строке находятся значения N, K и T, разделенные пробелами (1ЈNЈ100, 1ЈKЈ100, 0ЈTЈ30000).

Во второй строке находятся времена прихода посетителей T₁T₂ , ..., T_N, разделенные пробелами (0ЈT_iЈT, для всех i = 1, 2, ..., N).

В третьей строке находятся величины суммы денег у посетителей P₁, P₂, ..., P_N, разделенные пробелами (0ЈP_i<=300, для всех i = 1, 2, ..., N).

В четвертой строке находятся значения степени полноты посетителей S₁, S₂, ..., S_N, разделенные пробелами (1ЈS_iЈK для всех i = 1, 2, ..., N). Все исходные данные — целые числа.

Выходные данные

Выводится одно число — максимальная сумма денег у посетителей ресторана. В случае, если нельзя добиться прихода в ресторан ни одного посетителя, выходной файл должен содержать значение 0.

Пример входных данных:

4 10 20
10 16 8 16
10 11 15 1
10 7 1 8

Результат:

Пример входных данных:

2 17 100
5 0
50 33
6 1

Результат:

Решение

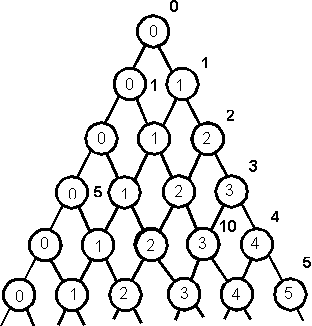
Это классическая задача на метод динамического программирования. Состояния открытости двери можно представить “треугольной решеткой”, изображенной на рисунке. Каждая вершина определяет степень открытости q в момент времени t. Некоторым вершинам решетки приписаны веса, равные сумме денег у посетителя, приходящего в момент времени t и имеющего степень полноты, равную q. Требуется найти путь по решетке, проходящий через вершины, сумма весов которых имеет максимальное значение. Следует отметить, что нет необходимости хранить оценки всех вершин. Нам необходимо подсчитать оценки для момента времени t. Это возможно, если известны их значения для всех предыдущих моментов времени, однако для подсчета достаточно помнить только оценки для момента времени t–1. Приведем более простой пример входных данных:

3 5 6
3 4 1
5 10 1
1 4 1

Соответствующая решетка приведена на рисунке. Справа на рисунке указаны моменты времени. Слева от некоторых вершин решетки приведены суммы денег у посетителей, приходящих в этот момент времени и имеющих степень полноты, совпадающей со степенью открытости двери, записанной в вершине решетки. Ответ для данного примера очевиден: 11.

Данные

Const MaxN=500;
MaxK=100;
Var N,K,Tend:Integer;
S,P,T:Array[0..MaxN] Of Integer;

Основная программа

Begin
Init;
Solve;
Done;
End.

Приведем только процедуру Solve, остальные достаточно очевидны.

Procedure Solve;
Var i,j:Integer;
SOld,SNew:Array[0..MaxK] Of LongInt;{массивы для формирования оценок вершин решетки}
Begin
   SOld[0]:=0;
   For i:=1 To K Do SOld[i]:=-MaxLongInt;
   SNew:=SOld;
   For i:=1 To Tend Do Begin
     {цикл по моментам времени}
     SNew[0]:=SOld[0];
     For j:=1 To i Do
     {цикл по достижимым состояниям решетки}
      SNew[j]:=Max(SOld[j-1],SOld[j]);
      {реализация функции Max очевидна}
     {формирование оценок вершин решетки}
     For j:=1 To N Do {цикл по посетителям}
      If (T[j]=i) And (SNew[S[j]]<>-MaxLongInt)
      {если время прихода посетителя совпадает
      с рассматриваемым моментом времени
      и состояние достижимо, то изменяем
      оценку вершины, соответствующей полноте
      посетителя}
      Then Inc(SNew[S[j]],P[j]);
      SOld:=SNew;{запоминаем массив оценок}
End;
Res:=-MaxLongInt;
For i:=1 To K Do Res:=Max(Res,SNew[i]);
{находим максимальное значение
   в окончательном массиве оценок}
End;