Задача "Разноцветные области" С.М.Окулов
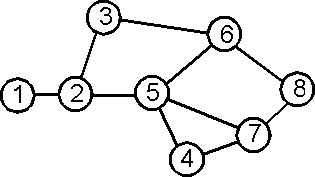
Дано прямоугольное клеточное поле M
ґ N клеток. Каждая клетка поля окрашена в один из шести цветов, причем верхняя левая и нижняя правая клетки имеют различные цвета. Две клетки одного цвета, имеющие общую сторону, считаются принадлежащими одной области. Таким образом, поле разбивается на некоторое количество областей.Правила игры. Вначале первый игрок находится в области, содержащей левую верхнюю клетку, второй — в области, содержащей правую нижнюю клетку. Игроки ходят по очереди. Делая ход, игрок перекрашивает свою область в любой из шести цветов.
В результате к области игрока присоединяются все прилегающие к ней области выбранного цвета, если такие имеются. Если после очередного хода окажется, что области игроков соприкасаются, игра заканчивается. Можно считать, что проигрывает тот, кто не может сделать ход, но суть задачи не в этом.
Требуется написать программу, которая определяет минимально возможное число ходов, за которые игра может завершиться.
Формат входных данных. Цвета пронумерованы от 1 до 6. Первая строка входного файла содержит размеры поля (1
Ј M, N Ј 50). Далее следует описание поля — M строк по N цифр (от 1 до 6) в каждой (без пробелов). Первая цифра соответствует цвету левой верхней клетки игрового поля. Количество областей не превосходит 50.Формат выходных данных. В выходной файл необходимо вывести искомое количество ходов.
Пример файлов входных и выходных данных.
INPUT.TXT
4 3
1 2 2
2 2 1
1 4 3
1 3 2
OUTPUT.TXT
3
Решение. Сведем задачу к некоторой графовой модели. Будем рассматривать идею решения на примере, приведенном в формулировке задачи. Преобразуем исходную матрицу (T) в матрицу областей (Ob), определим цвет каждой области (массив C) и подсчитаем количество областей (k). Для нашего примера массив Оb будет выглядеть следующим образом.
1 2 2
2 2 3
456
478
Массив
С — (1, 2, 1, 1, 4, 3, 3, 2), k равно 8. Затем по матрице построим матрицу смежности графа (G), определяющего связи между областями.
Рис. 1. Граф, определяющий связи
областей
(для нашего примера)
0 1 0 0 0 0 0 0
1 0 1 1 1 0 0 0
0 1 0 0 0 1 0 0
0 1 0 0 1 0 1 0
0 1 0 1 0 1 1 0
0 0 1 0 1 0 0 1
0 0 0 1 1 0 0 1
0 0 0 0 0 1 1 0
Рис. 2. Матрица связности графа
После этих замечаний решение задачи сводится к поиску кратчайшего пути, точнее, количества ребер в кратчайшем пути между начальной и конечной вершинами. Для этого можно использовать алгоритм Дейкстры или обход графа в ширину. Схема обхода графа в ширину приведена на рисунке. Рядом с вершинами в квадратных скобках указан уровень просмотра этой вершины. Ответ задачи — значение уровня конечной вершины минус единица.
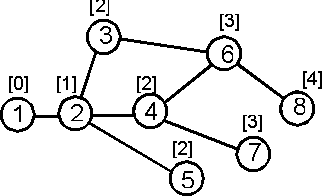
Рис. 3. Последовательность просмотра вершин графа
Приведем фрагменты реализации.
Procedure MakeG;В процедуре
Obl реализуется обычная схема поиска выхода из лабиринта. Procedure Obl(x,y,k:Integer);В данной рекурсивной процедуре используются массивы констант
Px и Py, которые имеют вид: Px:Array[1..4] Of ShortInt=(1,0,-1,0);При формировании матрицы
G используется алгоритм обхода связной области, т.е. области, заполненной одним значением метки в матрице Ob. Procedure Rec(x,y,k:Integer);Procedure MakeA;
Var Og,Nnew:Array[1..MaxOb{максимальное
количество областей}] of Byte;
yk1,yk2,i:integer;{указатели (записи,
чтения) для работы с очередью}
Begin
FillChar(Og,SizeOf(S),0);
FillChar(Nnew,SizeOf(Nnew),0);
yk1:=1;Og[yk1]:=1;Nnew[1]:=0;yk2:=0;
While yk2<yk1 Do Begin
Inc(yk2);
{выбираем очередной элемент из
очереди}
For i:=1 To NumObl Do
If (G[Og[yk2],i]=1) And (Nnew[i]=0) Then
Begin
Inc(yk1);Og[yk1]:=i;
Nnew[i]:=Nnew[Og[yk2]]+1;
End;
End;
{Nnew[NumObl]-1 — ответ}
End;