А.С.Пономаренко

Попробуем создать на экране монитора иллюзию вращения плоской кривой вокруг некоторой прямой в пространстве. Разберем несколько случаев:

1. Уравнение кривой задано параметрически, т.е. системой:

x = f(ф)        (1)
у = g(ф)        (2)

— где (ф — параметр. Вращать кривую будем вокруг оси OY.

Чтобы "заставить" кривую вращаться, достаточно постепенно изменять абсциссу х от максимального значения до минимального и обратно. Для этого уравнение (1) заменим уравнением (1'): х = f(ф) • cost, где значение t прямо пропорционально углу поворота вокруг оси OY. В качестве примера рассмотрим вращение "удлиненной циклоиды", которая задается системой:

х = а • ф — Ь • sin ф
 у == а—b • cos ф
 а < b

— где а и b — коэффициенты, определяющие размеры циклоиды.

Далее приводятся соответствующие программы на двух языках (QBasic и Turbo Pascal).

SCREEN 9: COLOR 14, 9 
 1 t = t + .05
       FOR f = 9.3 ТО -9.3 STEP -.2
               x = (20 * f - 40 * SIN(f)) * COS(t) + 320 
               у = -20 + 40 * COS(f) + 170 
              PSET (х, у), 14
        NEXT f

FOR i = 0 ТО 5000: NEXT: CLS 
IF INKEY$ = " " THEN END ELSE 1

Uses Crt,Graph;
            Procedure Graphinterface;
               var driver,mode,error:integer;
               s:string;
          begin
              driver:=detect;
              s: = ' ' ;
              Initgraph(driver,mode,s) ;
              error:=GraphResult;
              if error<>GrOk then
              begin
                   Writeln(GraphErrorMsg(Error));
                   Halt (error)
              end
           end;
Var
     x,y,p,t : real;
     f : :integer;
BEGIN
     Graphinterface;
     SetColor(14) ;
     SetBkColor (9) ;
     t:=0;
     repeat
        t:=t+0.05;
        for f:=93 downto -93 do
              begin
                  x:=(2*f-40*sin (f/10))*cos (t)+320;
                  y=-20+40*cos(f/10)+170;
                  putpixel(round(x),round(y),14);
              end;
      Clear viewport;
   until keypressed;
   CloseGraph;
END.

2. Рассмотрим теперь вращение кривой вокруг оси ОХ. Нетрудно догадаться, что в этом случае мы оставим уравнение (1) без изменений, а уравнение (2) заменим уравнением (2') : у == g(фj) •  cost. В качестве примера рассмотрим кривую, которая называется "Локон Марии Аньези" и задается системой:

x = 2а • ctgф
у = 2а • sin²ф

— где а — радиус окружности, которую огибает эта кривая.

SCREEN 9 : COLOR 14, 9 
1    t = t + .05
     FOR f=.5 TO 2.6 STEP .05
          х = 100*COS(f)/SIN(f) + 320
          у = -100*SIN(f)*SIN(f)*COS(t) + 170
          PSET (x,y), 14 
     NEXT f
     FOR i=0 TO 5000 : NEXT : CLS
      IF INKEY$ = " " THEN END ELSE 1

Uses Crt,Graph;
var
gd, gm : integer;
f, i : integer;
x, y, t : real;
   Procedure Graphinterface;
    var
      driver, mode, error : integer;
      s:string;
   begin
      driver:=detect;
      s: = ' ' ;
      Initgraph(driver,mode,s) ;
      error:=GraphResult;
      if error<>GrOk then
      begin
          Writeln(GraphErrorMsg(Error));
           Halt (error)
       end
    end;

BEGIN
   Graphinterface;
   SetBkColor(1) ;
     repeat
       t:=t+0.5;
       for f:=l to 600 do
       begin
          x:=100*cos (f/200)/sin (f/200)+320;
          y:=-100*sin(f/200)*sin(f/200)*cos (t)+170;
           putpixel(round(x),round(y),14);
       end;
       Clearviewport;
    until keypressed;
    CloseGraph;
END.

3. Пусть теперь уравнение кривой задано в полярных координатах, т.е. имеет вид р = р(ф), где (р — угол, принимающий значения из некоторого промежутка. Такое уравнение можно записать в параметрическом виде.

x=р(ф)•соsф     (3)
y=p(ф)•sinф       (4)

Поскольку вращать кривую вокруг осей координат мы умеем, попробуем "заставить" кривую вращаться вокруг начала координат. Для этого уравнение (3) преобразуем в уравнение (3'): х = р(ф) • cos(ф + t), Приведем пример программы для создания иллюзии вращения "трилистника" или "трехлепестковой розы" имеющей уравнение р = а • cos3ф, где а — радиус окружности, в которую вписана данная кривая:

SCREEN 9 : COLOR 14, 9
 1   t = t + .05
      FOR f=0 TO 6.28 STEP .1
           р = 120 * COS (3 * f)
           х = p*COS(f + t) + 320
           у = p*SIN(f) + 170

     PSET (x,y), 14
NEXT f

FOR i=0 TO 1000 : NEXT : CLS 
IF INKEY$ = " " THEN END ELSE 1

Uses Crt, Graph;

   Procedure Graphinterface;
    var
      driver, mode, error : integer;
      s:string;
   begin
      driver:=detect;
      s: = ' ' ;
      Initgraph(driver,mode,s) ;
      error:=GraphResult;
      if error<>GrOk then
      begin
          Writeln(GraphErrorMsg(Error));
           Halt (error)
       end
    end;

Var
     x, y, p, t : real;
     f : integer;
 BEGIN Graphinterface;
   SetColor(14) ;
   SetBkColor(9) ;
   t:=0;
   repeat
      t:=t+0.05;
      for f:=0 to 628 do
         begin
           p:=120*cos(0.3*f) ;
           x:=p*cos(f / 10 + t)+320;
           y:=p*sin(f / 10)+170;
           putpixel(round(x),round(y) , 14) ;
         end;
      Delay(100) ;
      Clearviewport;
   until keypressed;
   CloseGraph;
END.

4. В заключение приведем пример кривой, заданной уравнением вида f(x, у) = 0 (5).

Рассмотрим гиперболу, каноническое уравнение которой имеет вид:

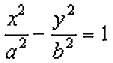
Заменой у = b • tgф данное уравнение приводим к системе:

x=a/cosф

у=b•tgф             (*)

Используя (*), легко составить программы вращения гиперболы вокруг осей координат или точки их пересечения (см. 1, 2 и 3). Но мы лучше рассмотрим еще один способ создания иллюзии перемещения кривой в пространстве. Будем "удалять" и "приближать" кривую. Для этого надо каждое из уравнений (1) и (2) заменить уравнениями (1') и (2').

SCREEN 9: COLOR 14, 9, 
1   t = t + .05
    FOR f = 0 ТО 6.28 STEP .08
         x = 80 * COS(t) / COS(f) + 320 
         у = -30 * TAN(f) * COS(t) + 170
         PSET (x, у), 14 NEXT f
     FOR i = О ТО 5000: NEXT: CLS 
 IF INKEY$ = " " THEN END ELSE 1

Uses Crt, Graph;

   Procedure Graphinterface;
    var
      driver, mode, error : integer;
      s:string;
   begin
      driver:=detect;
      s: = ' ' ;
      Initgraph(driver,mode,s) ;
      error:=GraphResult;
      if error<>GrOk then
      begin
          Writeln(GraphErrorMsg(Error));
           Halt (error)
       end
    end;

Var
     x, y, p, t : real;
     f : integer;
 BEGIN 
   Graphinterface;
   SetColor(14) ;
   SetBkColor(9) ;
   t:=0;
   repeat
      t:=t+0.05;
      for f:=0 to 628 do
         begin
           x:=80*cos(t)/cos(f / 10)+320;
           y:⁼-30*sin(f/10)/cos(f/10)*cos(t)+170;
            putpixel(round(x),round(y),14);
        end;
      Delay(10) ;
      Clearviewport;
   until keypressed;
   CloseGraph;
END.