Вычисление общего члена
последовательностей и их сумм
В.И. Ракитин
Данная публикация содержит:
— математические основы по теме
"Последовательности и ряды";
—алгоритмы решения некоторых типовых задач на
рассматриваемую тему и их запись на
алгоритмических языках QBasic, Паскаль, Си;
— программы для вычисления значений
многочленов в заданной точке.
1. Последовательности и способы их
задания. Ряды
Определение 1. Функция,
определенная на множестве натуральных чисел,
называется последовательностью.
Последовательность может быть
образована элементами любой природы,
занумерованными натуральными числами 1, 2, ..., an, ..., и записана в виде {а1, а2, ..., аn, ...},
или {an}, или аn. Будем рассматривать
только числовые последовательности, когда
каждому значению аргумента n соответствует
определенное число. Элемент последовательности an (элемент с номером n)
называют общим членом последовательности.
Последовательность может быть
определена:
1) формулой для общего члена
последовательности an =  (n);
(n);
2) рекуррентными соотношениями
(от лат. recurrens — возвращающийся). При этом
задаются несколько первых членов
последовательности и формулы, позволяющие
последовательно, шаг за шагом, определить любой
член последовательности. Таким образом, заданные
последовательности называют еще возвратными
последовательностями.
Например, заданы два первых члена
последовательности а1, а2 и
уравнение  (an-2, an-1, an) = 0. Тогда,
полагая п = 3, можно составить уравнение для
а3:
(an-2, an-1, an) = 0. Тогда,
полагая п = 3, можно составить уравнение для
а3:  (a1,
а2, а3) = 0, из которого найти
a3. Далее, полагая п =
4, из уравнения
(a1,
а2, а3) = 0, из которого найти
a3. Далее, полагая п =
4, из уравнения  (a2, a3, a4)= 0 находится
а4 и т.д.
(a2, a3, a4)= 0 находится
а4 и т.д.
Рекуррентные соотношения называют
рекурсивными функциями (от лат. recursio —
возвращение), если общий член последовательности
явно выражается через предшествующие члены
последовательности. В этом случае функции числа п
начиная с некоторого номера явно выражаются
через предыдущие значения этой же функции.
В некоторых частных случаях
последовательность можно определить как первым,
так и вторым способом, т.е. по формуле для общего
члена последовательности получить рекурсивную
функцию и наоборот.
Примеры последовательностей,
заданных формулой
1) an = a0
+ d(n-1) или {a0, a0 + d, a0 + 2d,
a0+ 3d, ..., а0 + {n - 1)d, ...}
— арифметическая прогрессия с разностью d 0. В частности, если a0 = 1 и d = 1,
имеем an= п
— последовательность натуральных чисел {1, 2, 3, 4,
..., n, ...};
0. В частности, если a0 = 1 и d = 1,
имеем an= п
— последовательность натуральных чисел {1, 2, 3, 4,
..., n, ...};
2) an = a0 • q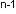 или
{a0, a0 • q, a0 • q
или
{a0, a0 • q, a0 • q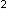 , a0 • q
, a0 • q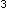 , ..., a0 • q
, ..., a0 • q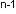 ), ...} — геометрическая прогрессия
со знаменателем прогрессии q
), ...} — геометрическая прогрессия
со знаменателем прогрессии q 0 и
0 и
q 1.
Например, для a0 = 2 и q = 2 имеем
an = 2
1.
Например, для a0 = 2 и q = 2 имеем
an = 2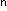 , т.е.
последовательность вида {2, 4, 8, 16, ..., 2
, т.е.
последовательность вида {2, 4, 8, 16, ..., 2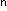 , ...};
, ...};
3) an = п! — последовательность п!
читается как "n факториал" (от англ. factor
— сомножитель) и определяется так:
0!= 1, n!=1•2•3• ... •n;
{1, 2, 6, 24, 120, ..., п!, ...};
4) an = 1 / (n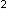 + 1) или {1/2, 1/5, 1/10, 1/17, ... ,1/(n
+ 1) или {1/2, 1/5, 1/10, 1/17, ... ,1/(n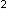 +2), ...}
+2), ...}
Примеры последовательностей, заданных
рекуррентными формулами (рекурсивными
функциями)
5) а1 = a0, an =
an-1 + d — арифметическая прогрессия с
разностью прогрессии d;
6) а1 = a0, an =
an-1 • q — геометрическая прогрессия со
знаменателем прогрессии q;
7) а1 = 1, an =
an-1 • n — последовательность "п факториал";
8) Если п < 3, то an = 1, в противном
случае an = an-1 +
an-2. Каждый элемент последовательности,
начиная с третьего, равен сумме двух
предшествующих. Эту последовательность {1, 1, 2, 3, 5,
8, 13, 21, ...} называют "числами Фибоначчи";
9) an = ln ( l + ln ( 2 + ln ( 3 + ... + ln ( n - 1 + lnn ) ...) ) )
или та же последовательность, записанная иначе:
an
= ln ( ln ( ln (...ln ( lnn+ п - 1 ) + ... + 3) +2) +1).
Элементы данной последовательности могут
быть выражены с помощью другой
последовательности bm, представляемой в виде
рекуррентных соотношений. Определим
последовательность bn, полагая
b1 = lnn и bk = ln (bk-1 + n - к + 1), где k = 2, 3,..., n. Элементы
последовательности bm представляют собой рекурсивную функцию,
аргументом которой является значение той же
функции.
Применяя рекурсии для bn и используя равенство
an = bn, вычислим
элемент последовательности an:
b1 = ln
n;
b2 =
ln (b1
+ п - 1) = ln ( ln n + n - 1);
b3 =
ln (b2
+ n - 2) = ln ( ln (ln n + п - 1) + п - 2);
... ... ... ... ... ... ... ... ...
... ... ... ;
an =
bn =
ln (bn-1 + 1) = ln ( ln ( ln ( ... ( ln ( ln n + n - 1 ) + ... ) + 3 )
+ 2 ) + 1 ).
Последовательности в примерах 5—8
определены с помощью рекурсивных функций.
Функции числа п, начиная с некоторого номера,
явно выражаются через предыдущие значения этой
же функции.
 (5) (n) =
(5) (n) =
 (5)
(n - 1) + d
(5)
(n - 1) + d
 (6) (n) =
(6) (n) =
 (6)
(n - 1) • q
(6)
(n - 1) • q
 (7) (n) =
(7) (n) =
 (7)
(n - 1) • n
(7)
(n - 1) • n
 (8) (n) =
(8) (n) =
 (8)
(n - 1) +
(8)
(n - 1) +  (8)
(n - 2)
(8)
(n - 2)
Определение 2. Формальную
сумму, составленную из элементов данной
последовательности an, называют рядом, а слагаемое с номером п
(общий член последовательности) называется
общим членом ряда. Ряд записывается в виде
а1 + а2 + а3 + ... + an + ... 
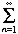 an
an
Можно определить частичные
суммы:
S1 = а1, S2 = а1 + а2, S3 = а1 + а2
+ а3, — и т.д.
Последовательность частичных сумм Sn естественно определяется
в виде рекуррентных соотношений:
S0 = 0, Sn = Sn-1 + an ( n = 1, 2, 3 ... )
или
S1 = а1, Sn = Sn-1 + an (
n = 2, 3, 4 ... )
Замечание. Иногда, определяя
ряд, выписывают несколько первых слагаемых ряда
с последующим многоточием без формулы для общего
члена ряда. Обязательно следует пополнить
задачу, заданную в виде "ребуса",
составлением либо формулы для общего члена ряда,
либо рекуррентного соотношения для него.
Подобрать формулу для общего
члена ряда
10)1/2•1 + 1/2•2
+ 1/2•3 + 1/2•4 + 1/2•5 + ... ,
11)1 + 1/2 + 1•2/4 + 1•2•3/8 + 1•2•3•4/16 + ... ,
12)1 + 1/4 + 1/12 + 1/32 + 1/80 + ...
Подобранные формулы таковы:
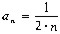 ,
,
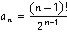 ,
,
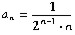 .
.
Представление ряда с
использованием аналитического выражения для
общего элемента последовательности
1/2•1 + 1/2•2 +
1/2•3 + ... + 1/2•n +
... = 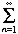 1/2•n ;
1/2•n ;
1 + 1/2 + 1•2/4 + ... + (n-1)!/2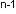 + ...
=
+ ...
= 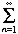 (n-1)!/2
(n-1)!/2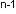 ;
;
1 + 1/4 + 1/12 + 1/32 + ... + 1/2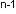 •n + ... =
•n + ... = 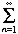 1/2
1/2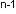 •n .
•n .
Замечание. При представлении
ряда нумерацию слагаемых часто начинают не с
единицы, а с нуля. Примеры одинаковых рядов,
имеющих различные формы записи из-за изменения
стартового значения счетчика:
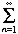 1/2•n =
1/2•n = 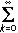 1/2•(k+1),
1/2•(k+1),
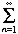 (n-1)!/2
(n-1)!/2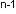 =
=
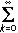 k!/2
k!/2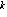 ,
,
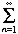 1/2
1/2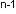 •n
=
•n
= 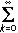 1/2
1/2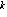 •(k+1).
•(k+1).
2. Программирование вычислений
последовательностей
2.1. Программы без подпрограмм
Задача 1. С клавиатуры вводятся
целые положительные числа п, р и а.
Составить программу для вычисления заданного
количества членов последовательностей п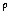 , а
, а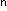 , n!. Вывести
на экран полученные значения.
, n!. Вывести
на экран полученные значения.
Решение. Будем использовать
переменную power (степень) для вычисления
степенной функции п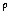 ; переменную exponent
(показатель) для вычисления показательной
функции а
; переменную exponent
(показатель) для вычисления показательной
функции а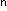 и переменную factor (множитель) для вычисления
факториала п!.
и переменную factor (множитель) для вычисления
факториала п!.
Программы состоят из:
• Блока описаний, где указываются
используемые модули, используемые переменные и
их типы;
• Тела программы, включающего;
— очистку экрана;
— ввод данных с клавиатуры;
— вычисление элементов
последовательности посредством рекуррентных
соотношений, стартовые значения переменных
таковы:
power = 1, exponent =
1, factor = 1,
формулы для общего
члена
poweri = poweri-11 • п,
exponenti = exponenti-11•
n,
factori
= factori-11 • i;
— вывод результатов на экран.
В программах переменные п, р и а —
целого типа integer (для неотрицательных целых чисел
диапазон их изменения от 0 до 32 767); переменные power,
exponent, factor — действительные числа с по крайней
мере 6—7 верными знаками после запятой (для
положительных чисел в допустимом для типа
диапазоне, например от 1,4 • (10-45) до 3,4 •
(1038) ).
Используемые типы данных имеют названия single, real,
float в языках Бейсик, Паскаль, Си соответственно.
При выходе какой-либо переменной за пределы
диапазона объявленного типа появляется
сообщение об ошибке переполнения (overflow).
Форматированный вывод результатов работы
программ на всех языках программирования
одинаков для примера, где п= 10, р=3, а= 3.
Имеем: n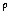 = lO
= lO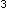 = 1000, а
= 1000, а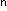 = 3^10 = 59 049, n! == 10! = 3 628 800.
= 3^10 = 59 049, n! == 10! = 3 628 800.
Программа на языке QBasic ;
'Блок описаний
DIM a AS INTEGER, i AS INTEGER, n AS INTEGER, p AS INTEGER
DIM power AS SINGLE, exponent AS SINGLE, factor AS SINGLE
'Тело программы: очистка экрана, ввод данных с
клавиатуры
CLS
INPUT "Введите число n = ", n
INPUT "Введите степень р = ", р
INPUT "Введите основание показательной функции а
= ", а
'вычисление элементов последовательности
посредством рекуррентных соотношений
power = 1: exponent = 1: factor = 1
FOR i = 1 ТО р
power = power * n
NEXT i
FOR i = 1 TO n
exponent = exponent * a
factor = factor * i
NEXT i
'вывод результатов на экран
st$ = "power=####.#,
exponent=#####.#,
factor=######.#"
PRINT USING st$; power; exponent; factor
Замечания к блоку описаний в
программе на языке QBasic
• Если для используемых переменных
не указан тип, то по умолчанию им присваивается
тип single.
• Если при определении типов
последовательно используются операторы
DEFINT
А, I, Р; DEFSGN E-F, Р,
то переменные, имена которых начинаются с A, I,
будут иметь тип integer, а переменные, имена которых
начинаются с E—F, Р, будут иметь тип single.
• Оператор
DIM
a, i, n, p AS INTEGER
не объявляет, что тип integer имеют все четыре
переменные. Переменные a, i, n будут иметь тип
single, и только переменная р будет иметь тип
integer.
Программа на языке Паскаль
{Блок описаний}
uses crt;
var a, i, n, p : integer;
power, exponent, factor: real;
{Тело программы}
begin
{очистка экрана, ввод данных с клавиатуры}
clrscr;
write ( 'Введите число n = ' ); readln(n);
write ( 'Введите степень р = ' ); readln(р);
write ( 'Введите основание показательной
функции а = ' ); readln (а);
{вычисление элементов последовательности
посредством рекуррентных соотношений}
power := 1; exponent := 1; factor ;= 1;
for i := 1 to p do power := power * n;
for i := 1 to n do
begin
exponent := exponent * a;
factor := factor * i
end;
{вывод результатов на
экран}
writeln ( 'power= ', power:1:1,
'exponent=
',exponent: 1:1,
'factor=',
factor:1:1 );
readln
end.
Программа на языке Си
/* Используемые модули */
#include <conio.h>
#include <stdio.h>
/*0сновная программа включает */
void main ( )
{
/*описание переменных, очистку экрана, ввод
данных с клавиатуры */
int a, i, n, p;
float power, exponent, factor ;
clrscr ( ) ;
printf ("Введите число n = ") ;
scanf ("%d", &n) ;
printf ("Введите степень р = ");
scanf ("%d", &p);
printf ("Введите основание
показательной функции а = "); scanf("%d",&а);
/*вычисление элементов последовательности
посредством рекуррентных соотношений */
power = exponent = factor = 1;
for (i = 1; i <= p; i++) power *= n;
for (i = 1; i <= n; i++)
{
exponent *= a;
factor *= i;
}
/*вывод результатов на экран */
printf ("power=%l.1f exponent=%l.1f
factor=%l.lf
\ n",
power,
exponent, factor) ;
getch( ) ;
}
2.2. Программы с подпрограммами-функциями
Рассмотрим вновь задачу 1 п. 2.1. Для
вычисления значений степенной и показательной
функций будем использовать подпрограмму-функцию
двух целых положительных переменных power (x, у) ,
возвращающую значение функции х^y, и
подпрограмму-функцию factor (x), возвращающую
факториал — x!. При вычислении элементов
последовательности в подпрограммах
используются рекуррентные соотношения п. 2.1.
Программа на языке QBasic
DECLARE FUNCTION power! (x AS INTEGER, у AS INTEGER)
DECLARE FUNCTION factor! (x AS INTEGER)
DIM A AS INTEGER, N AS INTEGER, P AS INTEGER
CLS
INPUT "Введите число n = ", n
INPUT "Введите степень p = ", p
INPUT "Введите основание показательной функции а
= ", а
st$ = "power=####.#,
exponent = #####.#,
factor=#######.#"
PRINT USING st$; power(n, p) ; power(a, n) ;
factor (n)
'Переменные i и у — локальные, используемые
только в подпрограмме
FUNCTION factor! (x-AS INTEGER)
DIM i AS INTEGER, у AS SINGLE
У = 1
FOR i = 1 TO x
у = у * i
NEXT i
factor = у
END FUNCTION
'Переменные i и z — локальные, используемые только
в подпрограмме
FUNCTION power! (x AS INTEGER, у AS INTEGER)
DIM i AS INTEGER, z AS SINGLE
z = 1
FOR i = 1 TO y
z = z * x
NEXT i
power = z
END FUNCTION
Программа на языке Паскаль
uses crt;
var a, n, p : integer;
{ Переменные i и у — локальные, используемые
только в подпрограмме }
function factor (x : integer) : real;
var i : integer;
y : real;
begin
y : =l;
for i : = 1 to x do у : = у * i;
factor : = y
end;
{ Переменные i и z — локальные, используемые
только в подпрограмме }
function power (x, y : integer) : real;
var i : integer;
z : real;
begin
z : = 1;
for i : =l to y do z := 2 * x;
power := z
end;
{Основная программа}
begin
clrscr;
write ( 'Введите число n = ' ); readln (n);
write ( 'Введите степень p = ' ); readln (p);
write ( 'Введите основание показательной
функции а = ' ); readln (a);
writeln ( 'power=', power (n, p) : 1 : 1,
'exponent=',
power (a, n) : 1 : 1,
'factor=',
factor (n) : 1 : 1 );
readln
end.
Программа на языке Си
#include <stdio.h>
#include <conio.h>
/* Переменные i и у — локальные, используемые
только в подпрограмме */
float factor (int x)
{
int i;
float y;
for (y=l, i = 1; i <= x; i++) y *= i;
return (y) ;
}
/* Переменные i и z — локальные, используемые
только в подпрограмме */
float power (int x, int y)
{
int i;
float z;
for (z=l, i = 1; i <= y; i++) z *= x;
return (z) ;
}
/*0сновная программа */
void main( )
{
int a, n, p;
clrscr ( ) ;
printf ("Введите число n = ");
scanf ("%d", &n);
printf ("Введите степень р = "); scanf
("%d",&p) ;
printf ("Введите основание
показательной функции а = "); scanf ("%d", &а) ;
printf ("power=%l. 1f exponent=%l. 1f factor=%l. lf\n",
power (n, p), power (a,
n), factor (n) ) ;
getch( ) ;
}
2.3. Полпрограммы-функции с рекурсией
Изменим теперь вид
подпрограмм-функций, используя рекурсивный
вызов функций. Оформление подпрограмм
практически соответствует математическому
определению рекурсивной функции: функция
вызывает из подпрограммы саму себя с
предшествующими значениями аргументов.
Подпрограммы на языке QBasic
'Подпрограмма-функция factor (х)
определена для неотрицательных х
FUNCTION factor! (x AS INTEGER)
IF х = 0 THEN
factor = 1
ELSE
factor = x*factor (x - 1)
END IF
END FUNCTION
'Подпрограмма-функция power (x, y) определена для
неотрицательных у
FUNCTION power! (x AS INTEGER, у AS INTEGER)
IF у = 0 THEN
power =1 ;
ELSE
power = x*power (x, у - 1)
END IF
END FUNCTION
Подпрограммы на языке Паскаль
{ Подпрограмма-функция factor(x) определена
для неотрицательных х}
function factor (x : integer) : real;
begin
if x = 0 then factor :=1
else factor:=x* factor (x-l)
end;
{Функция power (x, y) определена для неотрицательных
у}
function
power (x, у : integer) : real;
begin
if у = 0 then power:=1
else power := x * power (x, y-l)
end;
Подпрограммы на языке Си
/* Подпрограмма-функция factor(x)
определена для неотрицательных х */
float factor (int x)
{
if (x = 0) return(1) ;
else return (x*factor (x-1) );
}
/* Подпрограмма-функция power(x, y) определена для
неотрицательных у*/
float power (int x, int y)
{
if (y = 0) return(1) ;
else return (x*power (x, y-1) );
}
Замечание.
Рекурсивный вызов функций
иногда-существенно замедляет работу программы. В
этом можно убедиться, сравнивая работу двух
программ, вычисляющих числа Фибоначчи.
На любом из трех языков программирования
проведите вычисления чисел Фибоначчи при п = 5,
10, 20, 30 по двум программам. Программы отличаются
тем, что подпрограммы-функции для чисел
Фибоначчи fib (x) в одном из вариантов используют
рекурсивный вызов функции. Даже очень быстрые
компьютеры заметно "задумываются", проводя
вычисления по программе с рекурсией при п = 30.
Объясняется это тем, что рекурсивная функция для
нахождения fib (30) дважды вычисляет fib (28), ... 8 раз fib
(25) и т.д.
Программа, вычисляющая числа
Фибоначчи, на языке QBasic
DECLARE FUNCTION fib! (x AS INTEGER)
DIM N AS INTEGER
CLS
INPUT "n=", n
PRINT USING "fib (###) = ########"; n; fib (n)
FUNCTION fib! (x AS INTEGER)
DIM i AS INTEGER, DIM y AS SINGLE
DIM fib1 AS SINGLE, fib2 AS SINGLE
IF x < 3 THEN
fib = 1
ELSE
fib1 = 1: fib2 = 1
FOR i = 3 TO x
y
= fib1 + fib2
fib1
= fib2
fib2
= y
NEXT i
fib = y
END IF
END FUNCTION
Рекурсивная функция
FUNCTION fib! (x AS INTEGER)
IF x < 3 THEN
fib =1
ELSE
fib = fib (x - 1) + fib (x - 2)
END IF
END FUNCTION
Программа, вычисляющая числа
Фибоначчи, на языке Паскаль
program numbers_of_Fibonacci;
uses crt;
var n : integer;
function fib (x : integer) : real;
var i : integer;
y, fib1, fib2 : rea1;
begin
if x < 3 then
y :=1
else
begin
fib1:=l; fib2:=l;
for i:=3 to x do
begin
y:=fib1+fib2;
fib1:=fib2;
fib2:=y
end
end;
fib:=y
end;
begin
clrscr;
write ( 'n=' ); readln (n) ;
writeln ( 'fib ( ', n, ' ) =' , fib (n) : 10 : 0) ;
readln
end.
Рекурсивная функция
function fib (x : integer) : real;
begin
if x < 3 then
fib :=1
else
fib:=fib (x - 1) + fib (x - 2)
end;
Программа, вычисляющая числа
Фибоначчи, на языке Си
#include <stdio.h>
#include <conio.h>
float fib (int x)
{
int i;
float y, fib1, fib2;
if (x < 3)
y=1;
else ;
for (fib1 = fib2 = 1, i=3; i <= x; i++)
{ у = fib1+fib2; fib1 = fib2; fib2 = y; }
return (y) ;
}
void main( )
{
int n;
clrscr ( );
printf ("n = "); scanf ("%d", &n);
printf ("fib (%d) = %10.0f\n", n, fib (n) ) ;
getch ( ) ;
}
Рекурсивная функция
float fib (int x)
{
if (x < 3) return(1) ;
else return (fib (x-1) + fib (x-2) );
}
2. 4. Последовательность, элементы
которой — рекурсивные функции
Задача 2. Вычислить значение
выражения
аn = ln (1 + ln (2 +
ln (3 + ... + ln (n —1 + 4 + Inn) ...) ) ),
где п — некоторое натуральное число,
удовлетворяющее условию 5 <= п <= 20, причем
это число выбирается случайным образом в самой
программе.
Решение. В подпрограмме-функции а (x)
полностью воспроизведен алгоритм примера 9 п.1. В
основной программе используется функция,
называемая генератором случайных чисел: RND, или
random ( ) , в зависимости от языка программирования,
и процедура RANDOMIZE. Можно отметить, что
натуральный логарифм вычисляется в языках
Бейсик и Си библиотечной функцией log, а в языке
Паскаль — ln.
Программа на языке QBasic
DECLARE FUNCTION a! (x AS INTEGER)
'Основная программа
DIM n AS INTEGER
CLS
RANDOMIZE TIMER
n = 5 + INT (16 * RND)
PRINT n; " "; a(n)
'Подпрограмма, вычисляющая элемент
последовательности а(х)
FUNCTION a! (x AS INTEGER)
DIM k AS INTEGER
DIM b AS SINGLE
b = LOG (x)
FOR k = 2 TO x
b = LOG (b + x - k + 1)
NEXT k
a = b
END FUNCTION
Программа на языке Паскаль
uses crt;
var n : integer;
{Подпрограмма, вычисляющая элемент
последовательности а(x)}
function a (x : integer) : real;
var k : integer;
b : real;
begin
b := ln(x);
for k := 2 to x do
b := ln (b+x-k+l) ;
a := b
end;
{Основная программа}
begin
clrscr;
randomize;
n :=5 + random (16);
writeln (n, ' ', a (n) : 12 : 10);
readln
end.
Программа на языке Си
#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <stdlib.h>
/* Подпрограмма, вычисляющая элемент
последовательности а (х) */
float a (int x)
{ int k;
float b;
b = log (x) ;
for (k=2; k <= x; k++)
b = log (b+x-k+1) ;
return (y) ;
}
/*0сновная программа*/
void main( )
{ int n;
clrscr( ) ;
randomize( );
n =5 + random (16);
printf ("%d %12. 10f\n",n, a (n) ) ;
getch( ) ;
}
3. Программирование вычислений сумм
последовательностей
Задача
3. Пусть задана последовательность
an=(-1)n+1 ( n • 2n / (2n + 1)! ) ( n = 1, 2, 3, 4, … ).
Вычислить:
1.
Сумму п слагаемых данной последовательности;
число п вводится с клавиатуры.
2. Сумму
нечетных элементов последовательности; номера
которых не превосходят n.
3.
Сумму членов данной последовательности при
условии, что абсолютная погрешность вычисления
не больше 0,0001. Найти при
этом число слагаемых, образующих эту сумму.
Решение.
Обозначим через sum1, sum2 и sum3 переменные для сумм,
которые требуется найти в пунктах 1, 2 и 3
поставленной задачи. В программах это будут
переменные типа single, real, float (для языков Бейсик,
Паскаль, Си).
Вариант 1
Представим
выражение для общего члена последовательности в
виде an= -
n • (-2)n / (2n + 1)! .
Функция для вычисления
элементов данной последовательности выражается
через функции power и factor.
На языке QBasic
FUNCTION a# (x AS INTEGER)
а = -x*power (-2, x) / factor (2*x + 1)
END FUNCTION
На языке Паскаль
function a (x : integer) :
real;
begin
a:= -x*power (-2, x) / factor (2*x+l)
end;
На языке Си
float a (int x)
{return (-x*power (-2, x) / factor (2*x+l ) ) }
Вариант 2
He
представляет труда получить и запрограммировать
данную последовательность в виде рекуррентного
соотношения.
Прежде всего по
заданной формуле
an = (-1)N+1
( (n • 2n) / (2n + 1)! )
подставив в нее (n—1) вместо n, получим общий вид для
предшествующего члена последовательности
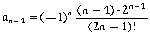
Далее
вычислим отношение
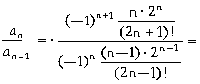
= (-1) [ (n • 2) / ( (n-1) • 2 •
n • (2n + 1) ) ] = - 1 / (n - 1) (2n +1),
учитывая, в частности при сокращении, что (2n + 1)! = 1 • 2 • 3 •
... • (2n - l)
• 2n • (2n +
1) = (2n - 1)! • 2n • (2n + 1).
И, наконец, присваивая
фактическое значение первому элементу a1 и выражая an через
an-1,
представляем данную последовательность в
рекуррентной форме:
a1 = 1/3, an
= an-1• ( -1 / (n-1) (2n+1) (n = 2, 3 …).
В
соответствий с полученными рекуррентными
формулами составлены подпрограммы-функции.
На языке QBasic
FUNCTION a! (x AS
INTEGER)
DIM i AS INTEGER, b AS single
IF x <= 1 THEN
b = 1 / 3
ELSE
b = 1 / 3
FOR j = 2 TO x
b = -b / ( j - 1 ) / ( 2*j + 1 )
NEXT j
END IF
a = b
END FUNCTION
На языке Паскаль
FUNCTION a (
x : integer ) : real;
var j : integer;
b : real;
begin
if x <= 1 then
b := 1 /
3
else
begin
b
:= 1 / 3;
for
j := 2 to x do
b
:=-b/ ( j – 1) / (2*j + 1)
end;
a
:= b
end;
На
языке
Си
float
a (int x)
{ int j;
float
b;
if
(x <= 1)
return
(1.0 / 3);
else
for
(b = 1.0 / 3,j = 2;j <=
х;
j++)
b*=-l.
0 / (j - 1) / (2*j + 1);
return
(b);
}
Замечания. В языке Си деление 1 / 3
дает целую часть от деления целых чисел, т. е. 0 в
данном случае, а деление 1, 0 / 3 возвращает 0,3333333 —
верный результат. Выражение —1 / (j - 1) / (2*j + 1) возвращало бы 0, а выражение —1, 0 /
(j - 1) / (2*j +
1) дает верный результат.
Программирование
вычисления сумм sum1, sum2 и sum3
При вычислении сумм
последовательностей аn используем
рекуррентные соотношения для
последовательности частичных сумм в виде.
S0 = 0, si = si-1
+ ai (I = 1, 2, 3, … ,n).
Абсолютной погрешностью вычисления
называется в данном случае dS = | Sn — Sn-1
| = | аn |. Таким
образом, мы будем суммировать элементы ряда до
тех пор, пока | аn | > 0,0001.
Очередным аn, модуль которого
меньше либо равен 0,0001, мы уже пренебрегаем. И тем
самым останавливаем процесс суммирования.
Программы для решения задачи 3 приведены ниже,
следует добавить только подпрограммы-функции а (x) для вычисления элементов
последовательности аn (например,
вариант 2).
Вычисление
сумм sum1, sum2, sum3
На языке QBasic
'Блок
описаний
DECLARE
FUNCTION a! (x AS INTEGER)
CONST
epsilon - .0001
DIM
i AS INTEGER, n AS INTEGER
DIM
sum1 AS SINGLE, sum2 AS SINGLE
DIM
sum3 AS SINGLE
'Основная
программа
CLS
INPUT
"Введите
n=", n
sum1=0
: sum2=0 : sum3=0
'Вычисление
sum1 и
sum2
FOR
i = 1 TO n
sum1 = sum1 + a ( i )
IF
i MOD 2 = 1 THEN
sum2
= sum2 + a( i )
END
IF
NEXT
i
'Вычисление
sumЗ
и числа слагаемых,
'образующих
сумму
i
= 1
DO
WHILE ABS ( a ( i ) ) > epsilon
sum3
= sum3 + a( i )
i
= i + l
LOOP
'He форматированный
вывод
результатов
PRINT
sum1, sum2, sum3
PRINT
i – 1
'Подпрограмма-функция
вычисления для an
FUNCTION
a!
(x
AS INTEGER)
…
На языке Паскаль
{Блок
описаний}
uses
crt;
const
epsilon = 0.0001;
var
i, n : integer;
sum1, sum2, sum3 :
real;
(Подпрограмма-функция
для
вычисления
an}
function
a (x : integer) : real;
… …
…
{Основная
программа}
begin
clrscr;
write {'Введите
n=');
readln (n);
sum1:=0; sum2:=0; sum3:=0;
{
{Вычисление
sum1 и
sum2}
for
i := 1 to n do
begin
sum1 :=
sum1 + a (i);
if
i mod 2 = 1 then
sum2
:= sum2 + a (i)
end;
{Вычисление
sum3 и числа слагаемых, образующих сумму}
i
:= 1;
while abs (a ( i ) )
> epsilon do
begin
sum3
:= sum3 + a (i);
i
:= i + 1
end;
{Форматированный
вывод
результатов}
writeln
('sum1=',
suml
: 8 : 7, ' sum2=',
sum2
: 8 : 7, ' sum3=',
sum3
: 8 : 7,' ', i - l);
readln
end.
На языке Си
/*Блок
описаний*/
#include
<stdio.h>
#include
<conio.h>
#include
<math.h>
#define
epsilon 0.0001
/*Подпрограмма-функция
для вычисления аn*/
float
a (int x)
… …
…
/*0сновная
программа*/
void
main ( )
{
int i, n;
float sum1,sum2,
sum3;
clrscr ( ) ;
printf ("n =
");
scanf
("%d", &n);
/*Вычисление
sum1 и
sum2*/
for (sum1 =
sum2 =0, i = 1;
i <=n;
i++)
{
sum1 +=a (i) ;
if
(i % 2 == 1)
sum2
+= a (i) ;
}
/*Вычисление
sum3 и числа слагаемых, образующих сумму*/
for (sum3 = 0, i=l;
fabs (a (i) ) >epsilon;
i++)
sum3 += a (i) ;
/*
Форматированный
вывод результатов */
printf ("sum1 = % 8.7f
sum2
= % 8.7f
sum3
= % 8.7f %d \ n",
sum1, sum2, sum3, i-1) ;
getch ( ) ;
}
Тестирование этой программы при п = 3 дает
следующие строки на экране:
Введите
n=3
sum1=0.
2714286 sum2=0. 3380952 sum3=0 .2712522 4
Замечание. Подпрограммы-функции,
отдельно вычисляющие значения элементов
последовательности, делают программу более
наглядной. Но программа становится менее
насыщенной повторами при вычислениях каждого
слагаемого, если в основной программе
воспроизводится следующий алгоритм:
a1
= 1/3, s1 = а1;
ai = ai-1• ( -1 / (i-1) (2i – 1) ),
si
= si-1+ ai (i
= 2, 3, ..., n).
В данном алгоритме
•
сначала первому элементу и сумме присваиваются
стартовые значения,
• затем
по рекуррентной формуле вычисляется следующее
слагаемое, которое и добавляется к предыдущему
значению суммы;
•
и далее необходимое число повторений вычислений.
Этот алгоритм,
например на языке Бейсик, реализуется с помощью
цикла со счетчиком FOR ... NEXT
…
DIM
b AS SINGLE
…
b
= 1 / 3 : sum1 = b : sum2 = b
FOR
i = 2 TO n
b = -b / (i -
1) / (2*i + l)
sum1 = sum1 +
b
IF l MOD 2=1 THEN
sum2
= sum2 + b
END IF
NEXT
I
…
4. Вычисление значения
многочлена
Определение 3. Функция вида
Pn(x) = a0xn + a1xn-1
+ a2xn-2 + … + an-1x + an (a0 0) называется многочленом, или полиномом, n-й степени. Любой
многочлен определяется
своей степенью и набором коэффициентов {а0,
a1, а2, ..., an-1, an }, а для его
вычисления необходимо еще задать значение
аргумента x.
0) называется многочленом, или полиномом, n-й степени. Любой
многочлен определяется
своей степенью и набором коэффициентов {а0,
a1, а2, ..., an-1, an }, а для его
вычисления необходимо еще задать значение
аргумента x.
В языках
программирования конечные последовательности
реализуются через структуру, называемую массивом,
Номер, определяющий конкретный элемент
массива, называется индексом. При описании
массивов определяются тип элементов массива и
диапазон его индексов. По умолчанию элементы
массива нумеруются с нуля (в языке Паскаль всегда
явное указание диапазона индексов). Массивы
естественно использовать в программах для
коэффициентов многочлена.
Задача 4. Составить программу
для вычисления значения многочлена в точке х. Степень
многочлена n, коэффициенты
многочлена
и
значение x вводятся с
клавиатуры.
Решение. Положим,
что переменная а — это массив коэффициентов
многочлена, его тип — single, real или float. Элементы
этого массива обозначаются — a (i) (для языка Бейсик)
или а [i] для Паскаля и Си (i = 0, 1, 2, ..., n).
При вычислении значения многочлена в
заданной точке x используется
алгоритм вычисления суммы. Остановимся на двух
различных схемах вычисления.
1-й вариант вычисления
значения многочлена
Вначале степенной
функции  присваивается
значение х0 = 1 , а сумме s — последнее
слагаемое аn. Далее
последовательно вычисляются значения степенной
функции при увеличении на 1 показателя степени и
сумма пополняется очередным слагаемым. В целом
алгоритм состоит из следующих шагов вычислений:
присваивается
значение х0 = 1 , а сумме s — последнее
слагаемое аn. Далее
последовательно вычисляются значения степенной
функции при увеличении на 1 показателя степени и
сумма пополняется очередным слагаемым. В целом
алгоритм состоит из следующих шагов вычислений:
Начальные значения:  0 =
1, S0 = аn .
0 =
1, S0 = аn .
1-й шаг:  1 =
1 =  0 • x = x, x = x,
0 • x = x, x = x,
s1 =
s0 + an-1•  1
= an-1x + an.
1
= an-1x + an.
2-й шаг:  2 =
2 =  1 • x = x x = x2,
1 • x = x x = x2,
s2 = s1 + an-2•
 2
= an-1x2 + an-1x
+ an.
2
= an-1x2 + an-1x
+ an.
3-й шаг:  3 =
3 =  2
•
x = x3,
2
•
x = x3,
s3 = s2 + an-3•
 3
= an-3x3 + an-2x2
+ an-1x + an.
3
= an-3x3 + an-2x2
+ an-1x + an.
…………………………………………………………..
n-й шаг:  n =
n =  n-1 • x = xn,
n-1 • x = xn,
sn = sn-1 + a0•
 n
= a0xn + a1xn-1
+ a2xn-2 + … + an-1x + an.
n
= a0xn + a1xn-1
+ a2xn-2 + … + an-1x + an.
Компактная запись
алгоритма выглядит так:
 0 = 1, s0 = an,
0 = 1, s0 = an,  i =
i =  i-1 • x,
i-1 • x,
s1 = si-1 + + an-1•  •
•  i (i = 1, 2, 3, …, n).
i (i = 1, 2, 3, …, n).
В
программах реализация этих вычислений выделена
жирным шрифтом
Программы
На
языке Qbasic
DIM i AS
INTEGER, n AS INTEGER
DIM f AS
SINGLE, s AS SINGLE
DIM x AS
SINGLE
DIM a (0 TO
10) AS SINGLE
CLS
INPUT "Введите n=", n
INPUT "Введите x=", x
PRINT "Введите "; n + 1;
PRINT " коэффициента
многочлена "; n; "степени "
FOR i = 0 ТО n
INPUT
"", a (i)
NEXT
f = 1: s =
a(n)
FOR i =1 TO n
f =f*x: s=s +
a (n - i) * f
NEXT i
PRINT USING
"#####"; s
На языке Паскаль
uses crt;
var i, n :
integer;
f,
s, x : real;
a : array[0..10] of real;
begin
clrscr;
write ('Введите n=');
readln (n);
write ('Введите х=');
readln (x) ;
writeln ('Введите
',n+l,
' коэффициента многочлена',
n,' степени ');
for i := 0 to
n do
readln
(a [i] );
f := 1; s :=
a[n];
for i := 1 to
n do
begin
f:=f*x; s:=s + a [n
- i]*f
end;
writeln
(s : 9 : 7);
readln
end.
На языке Си
#include
<stdio.h>
#include
<conio.h>
void main( )
{
int i, n;
float f, s,
x, a [10];
clrscr ( );
printf
("Введите
n="); scanf ("%d", &n) ;
printf
("Введите
x="); scanf ("%f", &x);
printf ("Введите %d
коэффициента многочлена %d степени \ n",n+1,n);
for (i=0;
i<=n; i++) scanf("%f", &a [i] );
for (f = l, s
= a [n], i =1; I <= n; i++)
{
f*=x; s+=a
[n-i] *f;
}
printf
("%9.7f \ n", s) ;
getch( ) ;
2-й
вариант вычисления значения многочлена — схема
Горнера
Рекуррентный
способ задания многочлена в виде
последовательно вычисляемых формул
Р0
= а0, Рi = Рi-1 • x + аi (i =1, 2, 3, .... n),
называют
схемой Горнера.
Эту схему вычислений
можно записать одним выражением: Рn = (...( ( a0x
+ a1)x
+ а2)x
+ ... + аn-1)x + аn.
Эти формы записи дают
следующие пошаговые вычисления значения
многочлена в точке x:
Схема Горнера
Р0
= a0
p1
= Р0
• x + a1
= a0x + a1
p2
= Р1
• x + a2
= a0x2 + a1x + a2
p3
= Р2
• x + a3
= a0x3 + a1x2 +
a2x + a3
…………………………………………………….
pn
= Рn-1
• x + an
= a0xn + a1xn-1
+ a2xn-2 + … + a + a + an-1x + an
Ниже приведены
фрагменты программы - реализации схемы Горнера.
На языке QBasic
Р
= а (0)
FOR i = 1 ТО n
Р = р * х + a (i)
NEXT i
На
языке Паскаль
Р
:= а[0]
;
for i := 1 to
n do
P
:= P * x + a [i] ;
На языке Си
P
= a [0];
for (i=l; i<=n; i++)
P = P * x + a
[i] ;
Тестирование
программы: пусть вычисляется значение
многочлена второй степени Р2(x) = х2
+ 2х + 3 при x = - 1 . Значение
многочлена равно 2. Результат действия программы
представляется на экране так:
Введите
n = 2
Введите х =
- 1
Введите 3
коэффициента многочлена 2-й степени
1
2
3
2
Замечание. Схема
Горнера позволяет вычислять значение полинома в
точке за минимальное количество операций +, -, *.
Литература
1. Йенсен К., Вирт Н. Паскаль. Руководство
для пользователя. М.: Финансы и статистика, 1989.
2. Керниган В.,
Ритчи Д. Язык программирования Си. М.: Финансы и
статистика, 1992,
3. Осипов С.В., Потемкин.
В.Г. MS-DOS 5.0.
QBasic. M.: Малип,
1992.
4. Попов В. Б. Турбо Паскаль для
школьников. Версия 7.0. ,М.: Финансы и статистика,
1998.
5. Уэйт М., Прата С,
Мартин Д. Язык Си. Руководство для начинающих.
М.: Мир, 1988.