"Математическое открытие"

В нашем "Книжном шкафу учителя информатики" есть множество книг, которые стоят в нем не потому, что мы учителя информатики, а просто потому, что мы учителя. Об одной из таких книг мы и хотим сегодня рассказать. Но сначала короткое отступление...

Лет десять или больше назад, не помню точно, сколько. Курс методики преподавания математики в пединституте. Я не очень хорошо помню сам курс, но два факта, к нему относящиеся, помню: та методика, которую нам читали, ничего, кроме смеха, не вызывала. Но мы зачитывали (к счастью, не до дыр, а то бы сейчас не о чем было рассказывать) книги, в которых излагалась совсем другая методика: Виленкина, Клейна, Пойя. Сегодня мы хотим познакомить вас с одной из лучших книг по методике (пусть методике преподавания математики — не суть важно). Речь идет о 'книге Джорджа Пойя "Математическое открытие", которая вышла в далеком уже 1970 году в издательстве "Наука" (нам, к сожалению, не удалось выяснить, переиздавалась ли она позднее, но в последние годы переизданий точно не было).

О чем эта книга? Если попробовать сформулировать кратко — о том, как решать задачи, о том, как учить решать задачи, и о том, как не бояться делать ни то, ни другое. Приведем короткие выдержки из авторского предисловия.

"Процесс решения задачи представляет собой поиск выхода из затруднения или пути обхода препятствия, — это процесс достижения цели, которая первоначально не кажется доступной. Решение задач является специфической особенностью интеллекта, а интеллект — это особый дар человека; поэтому решение задач может рассматриваться как одно из самых характерных проявлений человеческой деятельности. Цель настоящей книги состоит в том, чтобы разобраться в характере этой деятельности, найти средства для развития соответствующих способностей читателя и в конечном счете научить его лучше решать задачи. <...>

Решение задач — практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь.

<...> помните: если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!"

Конечно, учителю информатики с математическим образованием эта книга даст много больше, чем его коллеге без оного. Но даже если вы не имеете высшего образования по математике — прочитайте эту книгу, не пожалеете. Вы можете не вникать во все тонкости математических рассуждений, но обязательно почувствуете главное — глубокое убеждение автора в том, что владение предметом не достигается заучиванием формул, определений, клавиш (это мы уже от себя добавили). Владеть предметом — значит уметь и не 'бояться решать задачи.

Кроме того, что книга имеет огромную методическую ценность (которая для учителя информатики, на наш взгляд, в данном случае первична), в ней содержится достаточно много задач, которые могут пригодиться учителю и на уроках информатики. В частности, в теме "Интерполяция" очень подробно рассматривается многочлен Лагранжа, целая глава (третья) посвящена рекурсии (она так и называется — "Рекурсия"), в книге разобрано множество комбинаторных задач. Глава "Рекурсия" начинается с параграфа "История одного маленького открытия". Приведем небольшой фрагмент из него.

Существует традиционный рассказ о маленьком Гауссе, который впоследствии стал великим Карлом Фридрихом Гауссом. Мне очень нравится следующая версия, которую я слышал в детстве; вопрос о ее достоверности беспокоит меня весьма мало.

"Это случилось, когда маленький Гаусс еще посещал начальную школу. Однажды учитель задал нелегкую задачу: сложить числа 1, 2, 3 — и т.д. до 20. Он надеялся освободить себе немного времени, пока ученики будут заняты нахождением суммы такого длинного ряда чисел, и был поэтому неприятно удивлен, когда маленький Гаусс шагнул вперед — в то время, как остальные ученики еще только собирались приступить к работе, — положил грифельную доску на конторку учителя и сказал: "Готово". Учитель даже не взглянул на доску маленького Гаусса, так как был совершенно убежден, что ответ неверен, и собирался строго наказать мальчика за нескромность. Дождавшись, пока остальные ученики выполнили задание и сложили свои доски на доску маленького Гаусса, он вытащил ее (ведь она лежала в самом низу) и посмотрел. Каково же было удивление учителя, обнаружившего на Доске одно-единственное число и притом верное. Какое это было число и как, маленький Гаусс его нашел?"

Мы, конечно, точно не знаем, как маленький Гаусс это сделал, и никогда не сможем этого узнать. Однако воображение может подсказать нечто кажущееся правдоподобным. Как бы то ни было, Гаусс все же был тогда еще ребенком, хотя и очень умным и развитым не по летам. Возможно, что ему удавалось более непосредственно, чем другим детям такого же возраста, улавливать конечную цель задачи и сосредоточивать внимание на наиболее существенном. Весьма вероятно, что б данном случае он представил себе более четко и ясно, чем его сверстники что требуется в задаче, т.е. как найти сумму чисел 1, 2, 3, .... 20.

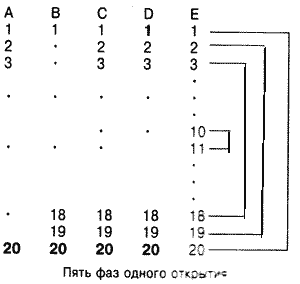
Он, должно быть, "видел" задачу не так, как другие, а более глубоко возможно, в таком духе, как это изображено на последовательности диаграмм А, В, С, D и Е, изображенных на рисунке.

В первоначальной формулировке задачи выписано в явном виде только начало ряда чисел, сумму которых требуется найти (А). Но мы могли бы указать также и конец ряда (Б) или, еще лучше, выписать начало и конец одновременно (С). В этом случае наше внимание могли бы привлечь два крайних числа: (самое первое и самое последнее) и. возможно, мы заметили бы, что существует некоторое соотношение, связывающее эти числа (D). А здесь уже открываема возможность появления идеи (Е). Да, это так, любая пара чисел, равноудаленных от концов, дает в сумме одно и то же число: 1 + 20 = 2 + 19 = 3 - 18 = ...- = = 10 + 11 = 21, и поэтому сумма ряда равна 10-21 =210.

Этим ли путем в действительности шел Гаусс?