Основы программирования
С.М. Окулов, г. Киров
Продолжение.
Начало см. здесь
Занятие 4.
Логический тип данных, побитовые операции над
целыми числами
План занятия:
•
обсуждение логического типа данных;
• обсуждение
побитовых операций;
• эксперименты с программами (построение
таблицы истинности, выполнение над целыми
числами);
• выполнение самостоятельной
работы.
Логический тип данных
Переменные лирического типа описываются
с помощью идентификатора Boolean. Они могут
принимать два значения: False (ложь) или True
(истина) ( False и True — стандартные
константы), под них выделяется 1 байт памяти.
Логический тип является перечислимым: False
< True, Ord(False) = 0, OrdTrue) = 1, Succ(False) = True,
Pred(True) = False.
В
Турбо Паскале имеются четыре логические
операции: логическое сложение, или,
дизъюнкция, — or;
логическое
умножение, или конъюнкция, — and; отрицание
— not, исключающее " или " (сложение
по модулю два) — хor.
Результаты
выполнения данных операций над переменными
логического типа приведены в таблице.
|
Значение операнда
|
Результат операций
|
|
x
|
y
|
not x
|
x and у
|
x or у
|
x xor y
|
|
False
|
False
|
True
|
False
|
False
|
False
|
|
False
|
True
|
True
|
False
|
True
|
True
|
|
True
|
False
|
False
|
False
|
True
|
True
|
|
True
|
True
|
False
|
True
|
True
|
False
|
Фактически выше приведены четыре
таблицы истинности сведенные в одну), с
помощью которых в математической логике
обычно описываются значения логических
функций.
Таблица
истинности устанавливает соответствие
между наборами значений переменных и
значениями логической функции.
Следует
четко понимать, что результатом выполнения
операций сравнения (отношения): < (меньше),
> (больше), <= (меньше или решаю), >= (больше
или равно),
<> (не равно), = (равно) является величина
логического типа. Ее значение равно True, если
отношение выполняется для для значений
входящих в него операндов, и False — в
противном случае.
В
Турбо Паскале нельзя вводить логические
данные с помощью оператора Read. Однако можно
выводить значения переменных логического
типа с помощью оператора Write.
Операции сдвига
Рассмотрим две операции над данными
целого типа: shl — сдвиг влево и shr —
сдвиг
вправо. В результате выполнения операции m
shl п значение
m сдвигается влево на n разрядов; в
результате выполнения операции m
shl п значение m сдвигается вправо на n
разрядов. При выполнении этих операций в
Турбо Паскале разряды, вышедшие за пределы
области памяти, выделяемой для типа данных,
теряются, а с другой стороны добавляются нули.
Например, если т
равно 32,
то сдвиг влево на один разряд дает 64, а сдвиг
вправо — 16. Операции сдвига на один разряд
равносильны умножению и делению нацело на
два.
Экспериментальный
раздел работы
1. Выполните обычные действия с
программой Му4_1 (набор, компиляцию, запись
на диск, запуск).
Program My4_1;
Uses Crt;
Var a,b:Boolean;
Begin
ClrScr;
a:=True;b:=True;
WriteLn (a : 6, b : 6, a and b :
6);
a:=True;b:=False;
WriteLn (a : 6, b : 6, a and b : 6);
a:=False;b:=True;
WriteLn (a : 6, b : 6, a and b : 6);
a:=False;b:=False;
WriteLn (a : 6, b : 6, a and b : 6);
ReadLn
End.
Примечание.
При
наборе программы не забывайте использовать команды работы с блоками.
Достаточно набрать a:=True; b:=True; WriteLn (a : 6, b : 6, a
and b : 6); затем выделить этот фрагмент
как блок, скопировать 3 раза и
модифицировать.
Измените программу, подставив в нее
остальные рассмотренные выше логические
операции.
2. Выполните обычные действия с программой
Му4_2 (набор, компиляцию, запись на диск,
запуск).
Program My4_2;
Uses Crt;
Var m, n : Integer;
Begin
ClrScr;
WriteLn ( ' Введите число и величину,
сдвига ' );
ReadLn (m, n);
WriteLn ( ' При сдвиге на ', n, ' разрядов
влево числа ' ,m, ' получаем число ' , m shl n);
WriteLn ( ' Введите число и величину
сдвига ' );
ReadLn (m, n);
WriteLn (При сдвиге на ' ,
n, ' разрядов вправо числа, ' ,m, ' получаем
число ' , m, shr n);
ReadLn
Ehd.
Убедитесь, что при вводе m =
32, n = 1 получаются числа 64 (результат
сдвига влево) и 16 (результат сдвига вправо).
Сдвиги вправо отрицательных чисел приводят
к интересным результатам. Например, если вы
введете -1 и 1 для того и другого сдвигов,
то получите -2 и 32 767. Если первый результат
вполне объясним, то для понимания второго
требуется вспомнить о представлении
отрицательных целых чисел в дополнительном
коде. Пусть у нас не 16 разрядов для
представления чисел (тип Integer), а 4.
Представление -1 в дополнительном коде есть
11112, Сдвиг вправо на один разряд
приводит к числу 01112, а это не что иное,
как 710.
3. Выполните обычные
действия с программой Му4_3, набрав только
первые три оператора WriteLn.
Program My4_3;
Uses Crt;
Begin
ClrScr;
WriteLn (1365 and 2730);
WriteLn (1365 or 2730);
WriteLn (1365 xor 2730);
WriteLn (1365 and $FF);
WriteLn (1365 and $FF0);
WriteLn (1365 and $FF00);
ReadLn
End.
Мы видим, что с величинами
типа Integer можно выполнять логические
операции, причем они выполняются
поразрядно над двоичными представлениями
чисел. Почему выбраны числа 1365 и 2730?
Переведите их в двоичную систему счисления:
136510 = 0101010101012, 273010 =
1010101010102 (рассматриваются только 12
младших разрядов). Операция
and дает в результате число
0, а операции or и хоr - 4095.
Поэкспериментируйте с программой.
Убедитесь, например, что
-256 and 255 = 0
-256 or 255 = -1
-256 xor 255 = -l
Попытайтесь
дать объяснение этим результатам.
Добавьте к программе следующие три
оператора WriteLn. В шестнадцатеричной системе
счисления для обозначения цифр
10, 11, 12, 13, 14, 15 используются
буквы латинского алфавита А, В, С, D, Е,
F. В
представлений F = 11112. Знак $ означает, что величина (константа)
записана в шестнадцатеричной системе
счисления. Запустите программу. Убедитесь в
том, что результаты операций равны
соответственно 85, 1360, 1280. Исследуйте
описанным способом в дополнительном коде
отрицательных целых чисел.
Заданий для самостоятельной
работы
1. В математической логике
известна функций следования, или
импликация (x Þ
у), ее
таблица истинности имеет вид
|
x
|
y
|
xÞ
у
|
|
False
|
False
|
True
|
|
False
|
True
|
True
|
|
True
|
False
|
False
|
|
True
|
True
|
True
|
Проверьте, что хÞу
эквивалентна not(x) or y. Составьте
программу проверки эквивалентности этих
двух логических функций.
2. В математической логике
известна функция Шеффера (x | у), ее таблица истинности
имеет вид :
|
x
|
y
|
x |
у
|
|
False
|
False
|
True
|
|
False
|
True
|
True
|
|
True
|
False
|
True
|
|
True
|
True
|
False
|
Проверьте, что х | у эквивалентна not(x)
or not(y). Составьте
программу проверки эквивалентности этих
двух логических функций.
3. В математической логике
известна фикция Вебба, или стрелка Пирса (хßу), ее таблица
истинности имеет вид
|
x
|
y
|
x ß
у
|
|
False
|
False
|
True
|
|
False
|
True
|
False
|
|
True
|
False
|
False
|
|
True
|
True
|
False
|
Проверьте, что хßу
эквивалентна not(x) and not(y). Составьте
программу проверки эквивалентности этих
двух логических фушфий.
4. Дана некоторая логическая
функция; например, (х Þ
у) Þ
z. Постройте таблицу истинности данной
функции. Схема построения приведена в
таблице. В первом столбце приведены
всевозможные наборы значений переменных х,
y и z (True обозначено еденицей, False—
нулем).
|
x y z
|
xÞy
|
(xÞy)
Þ
z
|
|
000
|
1
|
0
|
|
001
|
1
|
1
|
|
010
|
1
|
0
|
|
011
|
1
|
1
|
|
100
|
0
|
1
|
|
101
|
0
|
1
|
|
110
|
1
|
0
|
|
111
|
1
|
1
|
Преобразуйте эту формулу
в эквивалентную ей. Составьте программу
проверки эквивалентности этих двух
логических формул.
5. Постройте таблицы
истинности для следующих функций:
• (х | y) | z
• (x ß
y) ß
z
• (xÞy)
and z;
• not (x or not y and z);
• x and not (y or not z);
• not
(not x or у and z).
6. Дана логическая
функция (х ß
y) ß
(
z ß
v). Постройте ее
таблицу истинности.
|
x y z v
|
х ß
y
|
z
ß
v
|
(х ß
y) ß
( z ß
v)
|
|
0000
|
1
|
1
|
0
|
|
0001
|
1
|
0
|
0
|
|
0010
|
1
|
0
|
0
|
|
0011
|
1
|
0
|
0
|
|
0100
|
0
|
1
|
0
|
|
0101
|
0
|
0
|
1
|
|
0110
|
0
|
0
|
1
|
|
0111
|
0
|
0
|
1
|
|
1000
|
0
|
1
|
0
|
|
1001
|
0
|
0
|
1
|
|
1010
|
0
|
0
|
1
|
|
1011
|
0
|
0
|
1
|
|
1100
|
0
|
1
|
0
|
|
1101
|
0
|
0
|
1
|
|
1110
|
0
|
0
|
1
|
|
1111
|
0
|
0 |
1
|
Материал для чтения
1. Слово "логика"
употребляется в разных значениях, например,
логика событий, логика характера и т.д. Во
всех случаях имеется в виду определенная
последовательность и взаимозависимость
событий или поступков. Слово "логика"
употребляется и в связи с процессами
мышления. Основателем науки логика
считается древнегреческий философ
Аристотель (IV в. до н. э.), В XIX веке благодаря
работам английского ученого Джорджа Буля
возникла наука математическая логика.
Джордж Буль перенес на логику законы и
правила алгебраических действий, ввел
логические операции, предложил способ
записи высказываний в символической форме.
Алгебра логики — раздел математической
логики, изучающей строение (форму,
структуру) сложных высказываний и способы
установления их истинности с помощью
алгебраических методов.
Высказывание — повествовательное предложение,
относительно которого можно сказать, истинно
оно или ложно. Все
высказывания условно разделяются на
простые и составные. Составные
высказывания образуются из простых.
Например, высказывания х и
у —
простые, высказывание x and
у — составное.
2. Законы алгебры
логики позволяют производить
тождественные преобразования логических
выражений.
Основные законы
алгебры логики
(1) законы рефлексивности:
х or
х = х; x and x = x;
(2) законы коммутативности:
х or
у = у or х; х and у = у and х;
(3) законы ассоциативности:
х or (у or z — (х or у) or z
х and
(у and z) — (x and у)
and z;
(4) законы
дистрибутивности:
х and (у or z) = х and у or x and z;
х or (у and z) — (x or y) and (x
or z);
(5) закон двойного
отрицания:
not (not x) = x;
(6) законы де Моргана:
not (x and у) = not x or not у;
not (x or у) = not x and not у;
(7) законы поглощения:
х or x and y = x; x and (x or у) =
х;
(8) законы, определяющие
действия с логическими константами False и
True:
х or False = х;
х
and False = False;
х or
True = True;
x
and True = x;
not
False = True;
not
True = False;
not x
or_x — True;
not
x and x = False.
Из основных можно
вывести и другие законы, например:
(9) законы склеивания:
х and у or not x and y = у;
(х or у) and (not x or у) = у;
(10) закон Блейка —
Порецкого
x or not x and y = x or y
(11)
закон свертки логического выражения:
x and у or not x and z or y and z =
x and y or not x and z.
Примечания
1.
Приведем пример вывода закона Блейка —
Порецкого:
х or not x and у = х and True or
not x and у = х and (y or not y) or not x and y = x and y or x and not
y or not x and у = x and у or x and not у or not x and у or x and у = x or
у
2.
Упражнения для закрепления материала могут
быть следующими Даются логическое
выражение (например, not (not x or not y) = ?) и
варианты ответов: not x or у или х or у и т.д.,
- необходимо выбрать правильный ответ.
3.
Любую логическую функцию можно
преобразовать в:
•
дизъюнктивную нормальную форму (ДНФ);
•
конъюнктивную нормальную форму (КНФ).
В первом случае логическая функция
записывается в виде дизъюнкции конъюнкций,
образованных из переменных и их отрицаний.
Во втором случае наоборот.
Примеры:
not х оr у and z
х
and у and z or not у and not z (ДНФ)
x and (y or not z) — нет,
(not x or у) and z
x and у and (z or not v) (КНФ)
x and (y and z or not v) — нет
Сформулируем
алгоритм преобразования логической
функции к ДНФ:
• записать
функцию с использованием только
операций or, and y not;
• с
помощью законов де Моргала операцию
отрицания довести до отдельных
переменных и убрать выражения вида not
(not х) по закону двойного
отрицания;
• с
помощью первого закона
дистрибутивности убрать все
конъюнкции дизъюнкции и провести
поглощение.
В
результате получим ДНФ представления
логической функции для получения записи в
виде КНФ следует изменить третий пункт
алгоритма:
• с
помощью второго закона дистрибутивности
убрать все дизъюнкции конъюнкций и
провести поглощение.
Если все
конъюнкции в ДНФ содержат все логические
переменные или их отрицания, то ДНФ наpзывается
совершенной (СДНФ). Аналогично определяют и
совершенную КНФ (СКНФ)
Рассмотрим
построение совершенных ДНФ и КНФ на примере
функции (х Þ
y) Þ
not(z). Построим таблицу истинности данной
функции.
|
x y z
|
(х Þ
y) Þ
not(z)
|
|
000
|
1
|
|
001
|
0
|
|
010
|
1
|
|
011
|
0
|
|
100
|
1
|
|
101
|
1
|
|
110
|
1
|
|
111
|
0
|
СДНФ:
((xÞy)=
not z) = not x and not y and not z or not x and y and not z or x and not у and
not z or x and not у and z or x and у and not z.
СКНФ:
((xÞy)
= not z) = not(not x and not у and z) and not(not x and у and z) and not(x and
у and z) = (x or у or not z) and (x or not y) or not z) and (not x or
not у or not z).
Занятие 5.
Составной и условный операторы
План занятия:
• обсуждение составного и условного операторов;
• эксперименты с программами нахождения наибольшего из
двух и трех чисел;
• выполнение самостоятельной работы.
Составной оператор
Составной оператор
представляет собой последовательность операторов, выполняемых в том порядке, в
котором они записаны в программе. Он имеет следующий вид:
Begin оператор;
оператор;... оператор; End
Примечание. Разделитель
";" перед End можно не записывать.
Оператор If, или условный
оператор
Условный оператор может записываться в
полной и неполной форме.
полная форма условного оператора
If <условие> Then <оператор 1> Else <onepamop
2>
неполная форма условного оператора
If <условие>
Then <оператор>
Выполнение условного
оператора начинается с вычисления значения логического выражения, записанного в
условии. Как вы уже знаете, значением логического выражения является или True,
или False. В первом случае выполняется < оператор 1>,
во втором — < оператор 2>. В качестве < оператора 1>
или < оператора 2> может выступать любой оператор, в частности, и
составной оператор, и условный оператор. При использовании вложенных условных
операторов некоторые конструкции могут пониматься неоднозначно. Вот
соответствующий пример:
If <условие 1> Then <onepamop
1>
If <условие 2> Then <оператор 2>
Else <оператор 3>
Здесь неясно, к какому
оператору If относится ветвь Else. Эта неоднозначность разрешается по следующему
правилу: "Else относится к ближайшему оператору
If, у которого отсутствует
данная ветвь".
Экспериментальный раздел работы
1. Разбор условного
оператора можно выполнить на следующем простом примере.
Вывести на экран наибольшее из двух данных
чисел.
Program
Му5_1;
Var х, у: Integer;
Begin
WriteLn ( ' Введите 2 числа
' );
ReadLn (x, у);
If x>y Then WriteLn (x) Else WriteLn
(y);
ReadLn
End.
Поставьте
";" после оператора WriteLn (x) . Убедитесь, что появилась ошибка
"Error 113: Error in statement". Конструкция (оператор) If — Then —
Else неделима, поэтому разделитель ";" в ней недопустим. В случае
равенства чисел ваша программа выводит значение переменной у. Измените
программу так, чтобы в этом случае она выводила на экран сообщение "Числа
равны".
Попробуем найти наибольшее из трех чисел —
значения переменных х, у и z. Предположим, что все числа различны.
Возможны шесть различных случаев, они приведены на рисунке.
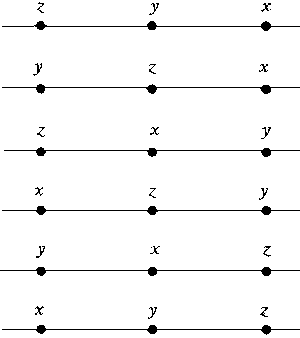
Программа определения значения
наибольшего из
трех чисел имеет вид:
Program My5_2;
Var x, у, z
: Integer;
Begin
WriteLn ( ' Введите три числа через пробел
' );
ReadLn (x, у, z);
If (x>y) And (x>z) Then WriteLn (x)
Else If (y>x) And (y>z) Then WriteLn (y)
Else WriteLn (z);
{ If x>y Then If x>z Then WriteLn (x)
Else WriteLn (z)
Else If y>z Then WriteLn (y)
Else WriteLn (z) ; }
ReadLn
End.
Вторая версия решения
заключена в фигурные скобки. Уберите их, заключите первую часть программы в
фигурные скобки и убедитесь в правильности второго решения. Измените программу
так, чтобы анализировался и случай равенства чисел. Обратите внимание на то,
что при написании сложных условий простые условия заключаются в скобки. Это
связано с тем, что операции сравнения имеют более низкий приоритет, чем
логические.
Задания для самостоятельной
работы
1. Имеется условный оператор:
If D<>10 Then writeln
( ' ура! ' )
Else Writeln ( ' плохо... ' );
Можно ли заменить его следующими операторами:
If D=10 Then Writeln ( '
ypa! ' )
Else Writeln ( ' плохо...' );
If
Not (D=10) Then Writeln ( ' ypa! ' )
Else Writeln ( ' плохо...' );
If Not (D=10) Then Writeln ( ' плохо...' )
Else Writeln ( ' ypa! ' );
If
Not (D<>10) Then Writeln ( ' плохо
...' )
Else Writeln( ' ypa! ' ).
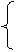 2. Запишите условный оператор, в котором значение переменной
с вычисляется по формуле: а + b, если а — нечетное и
а • b, если а — четное.
2. Запишите условный оператор, в котором значение переменной
с вычисляется по формуле: а + b, если а — нечетное и
а • b, если а — четное.
3. Вычислить значение функции:
хг + 5, при х > 3
х — 8, при х <= 3
4. Вывести на
экран номер четверти, которой принадлежит точка с координатами (x, у),
при условии, что x и у отличны от 0.
5. Дано
двузначное число. Написать программу определения:
• является ли сумма его цифр двузначным числом;
• превышает ли сумма
его цифр число X, которое вводится с клавиатуры;
• кратна ли сумма его цифр шести;
• больше ли цифра десятков цифры единиц;
• оканчивается ли число цифрой 5.
Придумайте не менее 8 аналогичных задач с
трехзначными числами.
6. Написать
фрагмент программы, в котором подсчитывается сумма только положительных чисел
из трех данных.
7. Написать
фрагмент программы, в котором подсчитывается количество четных чисел среди трех
данных.
8. Дано
трехзначное число. Написать программу определения, является ли оно палиндромом ("перевертышем"),
т.е. числом, десятичная запись которого читается одинаково слева направо и
справа налево.
9. Даны два
целых числа М и N. Если М делится нацело на N, то
вывести на экран частное от деления, в противном случае — сообщение "М
на N нацело не делится".
10. Даны два вещественных числа.
Уменьшить первое число в пять раз, если оно больше второго по абсолютной
величине.
11. Вычислить значение функции:
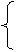 х — 12, при х > 0
х — 12, при х > 0
5, при х = 0
x2,
при х < 0
12. Даны три
различных целых числа, найти среднее из них. Средним назовем число, которое
больше наименьшего из данных чисел, но меньше наибольшего.
13. Составьте
программу нахождения произведения двух наибольших из трех введенных с
клавиатуры чисел.
14. Найти
количество положительных (отрицательных) чисел среди четырех целых чисел А, В,
С и D.
15. Дано двузначное
(трехзначное) число. Написать программу определения:
• входит ли в него цифра 5;
• входят ли в него цифры 4 и 7;
• входят ли в него цифры 3, 5,
7.
16. Даны целые
числа х и у. Написать программу определения знака разности х —
у. Саму разность при этом не вычислять. Разрешается сравнивать числа х
и у с нулем, а между собой можно сравнивать только модули чисел х
и у.
17. Известна
текущая дата. Пользователь вводит день, месяц и год своего рождения. Написать
программу определения, исполнилось ли пользователю полных 16 лет.
18. Написать
программу, определяющую, попадает ли точка с данными координатами в
заштрихованную область.
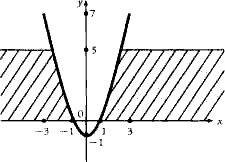
19. Написать программу,
определяющую, принадлежит ли точка заштрихованной области (уравнение окружности
х2 + y2= r2 ).
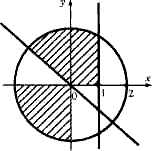
20. Составьте
программу вычисления выражений
max (x + y + z, xyz) + 3,
min (x2 + y2, y2 + z2)
- 4
Числа х,
y, z вводятся с клавиатуры.
21.
Составьте программу, которая из трех
введенных с клавиатуры чисел возводит в
квадрат положительные, а отрицательные
оставляет без изменения.
22.
Даны два конверта прямоугольной формы с
длинами сторон (а, b) и (с, d). Определить,
можно ли один из конвертов вложить в другой?
23.
Составьте программу, которая определяла
бы вид треугольника по длинам его сторон а, b
и с (если данные отрезки позволяют его
построить). Напомним, что если треугольник
может быть построен, одновременно
выполняются следующие условия: а + b > с, b +
с > а, а + с > b. Следует учесть,
что в качестве длин сторон могут быть
случайно введены как нулевые, так и
отрицательные значения.
Примечание.
Эту хорошо известную задачу
иногда называют тестом Г. Майерса на
профессиональную пригодность (он приведен
в его книге "Искусство тестирования
программ"). Если вы сможете в своей
программе проверить порядка 10 различных
случаев, то вам следует выбрать
программирование своей специальностью.
Материал
для чтения
1.
Давайте поговорим о том, чем мы пытаемся
заниматься, т.е. о программировании.
Приведем одно из определений: "Программирование
— теоретическая и практическая
деятельность по обеспечению программного
управления обработкой данных, включающая
создание программ, а также выбор структуры
и кодирования данных". Попробуем
определить то же несколько иначе, более
конструктивно, рассматривая то, чем
занимается программист.
Есть
задача или проблема. В первую очередь
программист должен определить возможность
ее решения, выбирая соответствующий метод.
Затем разработать алгоритм и программу на
каком-либо из языков программирования,
показать правильность работы программы и
предусмотреть возможность ее
совершенствования, внесения изменений на
этапе сопровождения. Таким образом, в
укрупненном виде мы видим три этапа: до
программирования, собственно
программирование и после программирования.
Только часть работы связана с выбором
структур данных и кодированием —
использованием языков программирования.
Программирование есть, если так можно
выразиться, инженерная работа по
конструированию некой целостной системы
обработки данных.
Отличие
программы, например, от некоторой
механической системы в том, что число
взаимодействующих частей в программе очень
велико, и проверить работу этой программной
системы, перебрать все возможные способы
взаимодействия ее частей в разумные сроки
немыслимо даже на сверхбыстродействующих
компьютерах. Где же выход? Видимо, только в
технологиях, обеспечивающих на выходе
качественный и надежный продукт.
"Технология
— совокупность методов обработки,
изготовления, изменения состояния, свойств,
форм сырья, материала или полуфабриката в
процессе производства, или наука о способах
воздействия на сырье, материалы или
полуфабрикаты соответствующими орудиями
производства". (Словарь иностранных слов.)
Приведем более подходящее для нас
определение.
"Технология
— это способ реализации сложного процесса
путем разделения его на систему
последовательных взаимосвязанных процедур
и операций, которые выполняются более или
менее однозначно и имеют целью достижение
высокой эффективности. Под процедурой
понимается набор действий (операций),
посредством которых осуществляется тот или
иной главный процесс (или его отдельный
этап), выражающий суть конкретной
технологии, а операция — это
непосредственное практическое решение
задачи в рамках данной процедуры, т.е.
однородная, логически неделимая часть
конкретного процесса".
В
нашем случае технология должна
поддерживать все три этапа работы
программиста, о которых речь шла выше, ибо
технология в данном случае есть искусство,
мастерство изготовления, конструирования
систем обработки данных. Обычно, когда
говорят о технологиях программирования, то
имеют в виду этап разработки программ,
первый и третий этапы не рассматриваются.
Действительно, можно считать этот этап
решающим, качественный выход на этом этапе
обеспечивает достаточную простоту
третьего этапа. Его часто трактуют как этап
сопровождения, но мы вкладываем более
широкий смысл — эволюционное изменение
системы обработки данных.
2.
Поговорим о простых и сложных программах.
Первые имеют ограниченную область
применения, разработаны и сопровождаются
одним человеком. Они могут быть
профессионально изготовлены, но так или
иначе они обозримы. Но не все программы
простые. Программы управления
железнодорожными или воздушными
сообщениями, системы управления базами
данных, обеспечивающими параллельный
доступ многих пользователей и т.д., — это
другой класс программ по уровню сложности.
Считается, что сложность программ отнюдь не
случайное свойство, скорее необходимое. Где
пролегает граница между простым и сложным?
Обычно сложность программ определяется
количеством операторов исходного текста
программы. Это условная градация, простая
количественная мера, которую можно принять
в качестве первого приближения. Известны
разработки программ с менее 10 000 операторов
исходного текста, относящиеся по
выполняемым функциям к сложным и даже
сверхсложным.
|
|
|
|
Программа
|
Количество
операторов
исходного текста (до)
|
|
Простая
|
1000
|
|
Средней сложности
|
10 000
|
|
Сложная
|
100 000
|
|
Сверхсложная
|
1 000 000
|
|
Гиперсложная
|
10 000 000 и более
|
Ограничимся
интуитивным пониманием простого и сложного.
Философский анализ этих понятий
применительно к программам — предмет
отдельного разговора. Отметим еще одну
особенность больших программ. Они имеют
тенденцию к эволюции в процессе их
использования. Это часто называют
сопровождением, но сопровождение есть
устранение ошибок, а эволюция
подразумевает внесение в программу
изменений, обусловленных изменяющимися
требованиями к ней.
Как
"бороться" со сложностью? Принцип
известен со времен древних римлян — "разделяй
и властвуй". Сложную задачу следует
разделить на взаимосвязанные подзадачи.
Последние, в свою очередь, опять
разделяются на свои подзадачи — и т.д. Зачем?
Во-первых, сложная задача (проблема, система)
описывается некой иерархической
структурой, во-вторых, определяются
принципы ее декомпозиции и, в-третьих, так
как каждый уровень — это определенный
уровень абстрагирования, создается
инструментарий для описания абстракций.
Иерархия — это ранжированная, или
упорядоченная, система абстракций,
расположение частей или элементов целого в
порядке от высшего к низшему. В результате
деятельности программиста создается
иерархическая структура из абстракций, а
"абстракция — это такие существенные
характеристики некоторого объекта, которые
отличают его от всех других видов объектов
и, таким образом, четко определяют
особенности данного объекта с точки зрения
дальнейшего рассмотрения и анализа". Г.Бруч
разделяет абстракцию сущности объекта —
объект представляет собой модель
существенных сторон предметной области и
абстракцию поведения — объект состоит из
обобщенного множества операций, каждая из
которых выполняет определенную функцию.
Другими
словами, сущность объекта мы описываем на
уровне данных в программе, а поведение —
действиями над этими данными.
3.
В этом и последующих материалах для чтения
мы коснемся истории развития технологий
программирования.
Операциональное
программирование
Этот
этап развития технологий программирования
характерен для ЭВМ первого поколения (с 1945-го
по 1959 год). Быстродействие ЭВМ этого
поколения составляло до 50 тысяч
арифметических операций, объем оперативной
памяти — в лучшем случае несколько
килобайт ячеек. Ресурсы минимальны. Если
сравнивать эти характеристики с
современными компьютерами: быстродействие
— миллиарды операций в секунду, объемы
памяти — мегабайты, — то различие
поразительно. ЭВМ того времени понимала
только цифровые команды, и программа
состояла из множества строк, состоящих из
цифр, интерпретируемых центральным
процессором. Например, 05 825 631 трактовалось
как команда сложения двух чисел (код 05),
записанных в ячейки с номерами 825 и 631.
Минимальные ресурсы ЭВМ требовали
строжайшей экономии оперативной памяти и
эффективных алгоритмов обработки.
Программы по взаимосвязи составных частей
обычно напоминали спагетти.
Надо
отдать должное программистам того времени.
Производительность их труда была очень
невелика, так как вручную необходимо было
распределить все переменные программы в
оперативной памяти (!).
Следующий
этап развития технологий программирования
мало отличается от первого. Он связан с ЭВМ
второго поколения. Появились языки
программирования типа ассемблера и
автокода. Теперь команда сложения
записывалась с использованием мнемоники —
ADD (сложить) PR1, ZET, где ADD — код команды, PR1, ZET
— имена ячеек. Перевод программы (трансляция),
записанной таким образом в цифровое
представление, а только такое понимает ЭВМ,
осуществлялся с помощью специальных
программ, называемых ассемблерами. Чем
характеризуется этот этап развития
технологий?
Первый и третий
этапы работы программиста не обсуждаются.
Программа "собирается" из мелких
деталей, отдельных операций и имеет
достаточно простую структуру. Уровень
абстрагирования — отдельное действие,
принципы декомпозиции задачи отсутствуют,
во всяком случае, о них не говорят.
Существует разрыв между требованиями
практики и возможностями программирования.
Круг решаемых с помощью ЭВМ задач
достаточно ограничен — в основном это
расчетные задачи.
Занятие 6.
Оператор For
План
занятия:
•
обсуждение
оператора
цикла For;
• разбор
программ
(рассматриваются
две программы;
в первой
проверяется,
является ли данное
число
палиндромом,
во второй —
есть ли в
записи числа
ровно три
одинаковые
цифры);
•
выполнение
самостоятельной
работы.
Оператор For
Оператор
цикла For
задает
многократное
выполнение
некоторого
оператора
(который может
быть и
составным) с
одновременным
изменением
значения
управляющей
переменной. Он
имеет
следующий
вид:
For <управляющая
переменная> := A
To B Do <оператор>
или
For <управляющая
переменная> := A DownTo В Do <onepamop>.
Здесь А —
начальное
значение
управляющей
переменной,
В —
конечное
значение
управляющей
переменной.
Начальное
(А) и конечное
(В) значения
управляющей
переменной
могут быть
представлены
любыми
выражениями,
тип которых
должен
совпадать с
типом управляющей
переменной.
Эти значения
определяются
один раз в
начале
выполнения
оператора For и
не
изменяются
во время
выполнения
этого
оператора.
Если
окажется, что
А > В при использовании
слова То, то
оператор
после слова Do
("тело" цикла)
не будет
выполнен ни
разу и выполнение
цикла сразу
же
закончится
(соответственно
при
использовании
DownТо цикл не выполнится,
если А < В),
Отметим еще
раз, что управляющая
переменная, а
также А и В
должны быть
одною типа,
причем
обязательно
порядкового.
Оператор
после слова Do
выполняется
один раз для
каждого
значения управляющей
переменной
из диапазона,
определяемого
значениями А
и В. Если в
операторе For, используется
слово То, то
значение
управляющей
переменной
увеличивается
на единицу
при каждом
повторении А,
А + 1, ..., В — 1, В, при DownTo —
уменьшается
на единицу.
Рекомендации
по
использованию
Оператор For
применяют
тогда, когда
известно
число
повторений
некоторого
действия (оператора).
Изменение
значения
управляющей
переменной в
теле цикл
может
привести к
ошибкам (некоторые
компиляторы
Паскаля
просто
запрещают
изменять
управляющую
переменную).
Поэтому
договоримся
о том, что это
действие
запрещено
законом, т.е.
учителем. Управляющая
переменная
после
выполнения
оператора For
не имеет определенного
значения (на
самом деле
она имеет
значение В,
но
стандартом
языка это не
оговорено).
Запретим
использование
ее значения
для анализа
чего-либо
после выполнения
оператора For, а
также
"искусственные"
выходы из For с
помощью
операторов Goto,
Exit и т.д. Оператор
For должен
иметь одну
точку входа и
одну точку
выхода.
Экспериментальный
раздел
работы
1.
Дано
натуральное
число п (п <= 9999).
Определить,
является ли
оно
палиндромом (
"перевертышем"
), с учетом
четырех цифр.
Например,
палиндромами
являются
числа: 2222, 6116, 0440.
Начнем
не с
написания
программы, а
с ручной трассировки
логики
решения. Это
очень важно.
Таким
образом, мы с
вами должны
достичь того,
чтобы при
написании
программы у
вас одновременно
складывался
"зрительный
образ" ее работы,
вы видели ее
работу,
причем это
должна быть
не
статическая
"картинка", а
динамическая.
Трассировка
обычно
выполняется
для
конкретных
значений
входных
параметров
задачи.
Итак, у
нас
четырехзначное
число, поэтому
переменная
оператора For
изменяется
от 1 до 4. В
переменной с
именем т хранится
"остаток"
числа,
сначала он
равен
введенному
числу. В
переменной с
именем r формируем
значение
числа-"перевертыша".
Основными
операциями
являются: r := 10*r + m Mod 10
(добавление
очередной
цифры к
числу-"перевертышу"
) и m: = m Div 10
(изменение
проверяемого
числа). Результат
трассировки
приведен в
таблице.
|
i
|
т
|
r
|
|
-
|
3994
|
0
|
|
1
|
399
|
0 • 10 + 3994 mod 10 = 0 + 4 = 4
|
|
2
|
39
|
4 • 10 + 399 mod 10 = 40 + 9 = 49
|
|
3
|
3
|
49 • 10 + 39 mod 10 = 490 + 9 = 499
|
|
4
|
0
|
499 • 10+3 mod 10 = 4990 + 3 = 4993
|
Program My6_1;
Var n, m, r, i : Integer;
Begin
WriteLn ('Введите целое число, меньшее 10 000');
ReadLn (n);
m: =n; r := 0;
For i:=1 To 4 Do
Begin
{так как число четырехзначное}
r:=r*10+m
Mod 10; m:=m Div 10
End;
If r=n Then
WriteLn ('ДА')
Else WriteLn ('НЕТ');
ReadLn
End.
Измените
программу
так, чтобы
можно было
обрабатывать
целые числа
из диапазона
LongInt.
2. Даны
натуральные
числа п, k (п, k <= 9999).
Из чисел от п до
k выбрать те,
запись
которых
содержит
ровно три
одинаковых
цифры.
Например,
числа 6766, 5444, 0006, 0060 содержат
ровно три
одинаковых
цифры.
Если
данное число
содержит
ровно три
одинаковых
цифры, то
только одна
из цифр
отличается
от остальных,
то есть
возможны
четыре случая,
приведенных
в таблице.
|
номер
цифры
|
1
|
2
|
3
|
4
|
|
1
|
X
|
X
|
X
|
|
|
2
|
X
|
X
|
|
X
|
|
3
|
X
|
|
X
|
X
|
|
4
|
|
X
|
X
|
X
|
— первое
условие
— второе
условие
— третье
условие
— четвертое
условие
Пусть
в качестве п и
k введены
числа 3732 и 3740. В
переменных a1,
a2 a3, a4 будем
хранить
значения
цифр
текущего числа
i.
|
i
|
а1
|
а2
|
аЗ
|
а4
|
Результат
сравнения
|
|
3732
|
3
|
7
|
3
|
2
|
ложь
|
|
3733
|
3
|
7
|
3
|
3
|
истина
|
|
3734
|
3
|
7
|
3
|
4
|
ложь
|
|
3735
|
3
|
7
|
3
|
5
|
ложь
|
|
3736
|
3
|
7
|
3
|
6
|
ложь
|
|
3737
|
3
|
7
|
3
|
7
|
ложь
|
|
3738
|
3
|
7
|
3
|
8
|
ложь
|
|
3739
|
3
|
7
|
3
|
9
|
ложь
|
|
3740
|
3
|
7
|
4
|
0
|
ложь
|
Примечание.
Пусть вас не
смущает
"элементарность"
выполняемых
действий.
Вспомните
одно из качеств
"великого
программиста".
Program Муб_2;
Var n, k, i, a1, a2, a3, a4, m :Integer;
Begin
WriteLn ('Введите
два числа, не
больших 9999');
ReadLn (n, k) ;
For i:=n
To k Do Begin
m : = i ;
{выделение цифр: a1 — первая, a2 — вторая,
аЗ — третья, а4 — четвертая}
a4:=m Mod 10;
m:=m
Div 10;
a3:=m Mod 10; m:=m Div 10;
a2:=m Mod 10;
a1:=m Div 10;
If ((a1=a2) And
(a1=a3) And
(a1<>a4))
{первое условие} Or
((a1=a2) And (a1=a4) And (a1<>a3))
{второе условие} Or
((a1=a3) And (a1 = a4) And (a1<>a2))
{третье условие} Or
((a2=a3) And
(a2=a4) And (a2<>a1))
{четвертое условие}
Then WriteLn
(i
:
5)
End;
ReadLn
End.
Измените
программу
для
обработки 4-, 5-
или 6-значных
чисел. Если
ваше решение
будет идейно
копировать
приведенное,
то это
хорошо, но не
очень. Оно
будет
достаточно
громоздким.
Постарайтесь
найти другое
решение, его
не обязательно
оформлять в
виде
программы.
Задания
для
самостоятельной
работы
Перед
написанием
программ
требуется
выполнить
ручную
трассировку
основных
фрагментов
решения.
1. Найти все
двузначные
числа,
которые
делятся на N
или содержат
цифру N.
2.
Составить
программу
вычисления
значения
выражения у = ((...(202
- 192)2 - 182)2 - ... - 12)2.
3.
Составить
программу
возведения
натурального
числа в
квадрат,
используя
следующую
закономерность:
12= 1
22 = 1 + 3
32 = 1 + 3+ 5
42 =1+3 + 5 + 7
n2= 1 + 3+ 5+ 7+ 9+ ... + (2n -
1)
4.
Определить
количество
трехзначных
натуральных
чисел, сумма
цифр которых
равна заданному
числу N.
5.
Составить
программу
вычисления
суммы кубов
чисел от 25 до 55.
6.
Среди
двузначных
чисел найти
те, сумма квадратов
цифр которых
делится на 13.
7.
Написать
программу
поиска
двузначных
чисел,
удовлетворяющих
следующему
условию: если
к сумме цифр
числа
прибавить
квадрат этой
суммы, то
получится
само число.
8.
Написать
программу
поиска
трехзначных
чисел,
квадрат
которых
оканчивается
тремя цифрами,
составляющими
исходное
число.
9.
Написать
программу
поиска
четырехзначною
числа,
которое при
делении на 133
дает в остатке
125, а при
делении на 134
дает в
остатке 111.
10.
Найти сумму
положительных
нечетных
чисел,
меньших 100.
11.
Найти сумму
целых
положительных
чисел из
промежутка
от А до В,
кратных 4
(значения переменных
А и В
вводятся с
клавиатуры).
12.
Найти сумму
целых
положительных
чисел,
больших 20,
меньших 100,
кратных 3 и
заканчивающихся
на 2, 4 или 8.
13. В
трехзначном
числе
зачеркнули
старшую цифру,
когда
полученное
двузначное
число умножили
на 7, то
получили
данное число.
Найти это
число.
14. Сумма цифр
трехзначного
числа кратна
7, само число
также
делится на 7.
Найти все такие
числа.
15.
Среди
четырехзначных
чисел
выбрать те, у которых
все четыре
цифры
различны.
16.
Среди
двузначных
чисел найти
те, которые делятся
на число q, а
сумма их цифр
равна п (0 < п <= 18).
17.
Дано
четырехзначное
число n.
Выбросить из
записи числа п
цифры 0 и 5,
оставив
прежним
порядок
остальных
цифр.
Например, из
числа 1509
должно
получиться 19.
18.
Натуральное
число из п цифр
является
числом
Армстронга,
если сумма
его цифр,
возведенных
в n-ю степень,
равна самому
числу
(например, 153 = 13
+ 53 + З3).
Получить все
трех- и
четырехзначные
числа
Армстронга.
19.
Дана
последовательность
из 20 целых
чисел. Определить
количество
чисел в
наиболее длинной
подпоследовательности
из подряд идущих
нулей.
20.
Дано
натуральное
число. Найти
все его
делители и их
сумму.
Материал
для чтения
Из
истории
программирования.
О
нисходящем
проектировании
программ, структурном
и модульном
программировании
Третье
поколение
ЭВМ (именно к
этому поколению
относится
знаменитая IBM/360)
отличало
использование
интегральных
схем. Большую
роль
начинают
играть
операционные
системы, на
которые
возлагаются
задачи управления
работой
компьютера.
Операционные
системы —
ядро
системного
программного
обеспечения.
Развиваются
языки
программирования
высокого
уровня. Если
первые
версии FORTRAN I, ALGOL-58
обеспечивали
лишь запись
математических
формул, то в
новом
поколении
языков
реализуются
новые идеи:
подпрограммы
и раздельная
компиляция (FORTRAN
II); блочная
структура и
типы данных (ALGOL-60);
описание данных
и работа с
файлами (COBOL);
обработка
списков и
указатели (Lisp). В
следующих
версиях
языков
продолжается
развитие: PL/1 (FORTRAN + ALGOL
+ COBOL), ALGOL-68 (преемник
ALGOL-60), Pascal (развитие
ALGOL-60), Simula (классы,
абстрактные
данные).
Возможности
языков
программирования
обеспечивают
поддержку нисходящей
технологии
конструирования
программ. Суть
нисходящего
конструирования
программ
состоит в
разбиении
большой
задачи на подзадачи,
которые
могут
рассматриваться
отдельно.
Основными
правилами
для успешного
применения
данной
технологии являются:
•
формализованное
и строгое
описание
программистом
входов
функций и
выходов всех
модулей
программы и
системы;
•
согласованная
разработка
структур
данных и
алгоритмов;
•
ограничение
на размер
модулей.
Нисходящая
технология
разработки
программ не
есть свод
жестких
правил,
скорее это
основной принцип,
допускающий
вариации в
соответствии
с
конкретными особенностями
решаемой
задачи. В
свое время в
обширной
литературе
по этому
поводу говорилось
и о восходящей
технологии.
В этом случае
решение
(программа)
как бы
"складывалось
из отдельных
кирпичиков",
из известных
решений
подзадач.
Таким образом,
данной
технологией
оговаривается
определенный
принцип
декомпозиции
и иерархическая
структура
программы.
Важнейшей
составляющей
этой
технологии
является структурное
программирование
(языки
программирования
Паскаль,
Модула-2). Пионером
структурного
программирования
был
Э.Дейкстра. В 1965
году он
высказал
предположение
о том, что
оператор
безусловного
перехода Goto
может быть
исключен из
языков
программирования.
Разумеется,
структурное
программирование
представляет
собой нечто
большее, чем
один лишь
отказ от
оператора Goto.
Структурное
программирование
— это
некоторые
принципы
написания
программ.
Теоретическими
основаниями
структурного
программирования
являются:
•
формальные
системы
теории
вычислимости
(операторные
схемы
программы
А.А. Ляпунова, системы
Поста,
алгоритмы
Маркова,
исчисление
Чёрча);
•
анализ
программ по
нисходящей
схеме, декомпозиция,
основанная
на разбивке
задач по уровням.
В
классической
работе Бома и
Джакопини
показано, что
такая
структура
(иерархическая,
разбитая на
уровни) может
быть реализована
в языке,
включающем
только ограниченное
число
управляющих
конструкций.
Для
реализации
программ
требуются
три основных
составляющих
блока,
которые
показаны
ниже.
Функциональный
блок, или
конструкция
следования.

Конструкция
обобщенного
цикла.
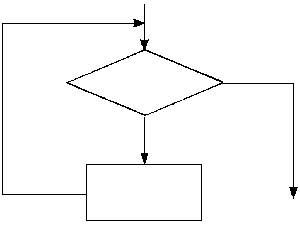
Конструкция
принятия
двоичного,
или дихотомического,
решения.
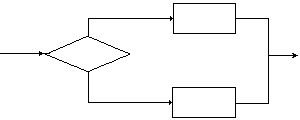
Характерные
черты
структурного
стиля программирования:
•
простота и ясность
(программа
легко
читается и анализируется);
•
использование
только
базовых
конструкций;
•
отсутствие
сетевых
структур в
программе;
•
отсутствие
многоцелевых
функциональных
блоков;
•
отсутствие
неоправданно
сложных
арифметических
и
логических
конструкций;
•
расположение
в строке
программы не
более одного
оператора
языка
программирования;
•
содержательность
имен
переменных.
При
этом процесс
нисходящей
разработки программы
может
продолжаться
до тех пор, пока
не будет
достигнут
уровень
"атомарных"
блоков, т.е.
базовых
конструкций
(присвоения, if-then-else, do-while).
Итак,
если
сформулировать
суть в сжатом
виде, то в
структурном
программировании
уточнен
принцип
декомпозиции
задачи (в
основном ее
алгоритмического
аспекта,
управляющей
компоненты,
т.е. действий,
однако
уровень
интеграции
действий и
данных "на
совести"
разработчика)
и сделана
попытка его
строгой
формализации.
К нисходящей
технологии
следует
отнести и то, что
называется модульным
программированием.
Достаточно
независимые
фрагменты
задачи оформляются
как модули.
Создаются
библиотеки модулей,
определяется
механизм
включения модулей
в
разрабатываемую
программу.
Модуль
должен иметь
строго
определенный
интерфейс и
скрытую
часть, одну
точку входа и
одну точку
выхода. Из
фольклора computer
science — "модульность
в
программировании
подобна честности
в политике:
каждый
утверждает, что
она — одно из
его
достоинств,
но, кажется, никто
не знает, что
она собой
представляет,
как ее
привить,
обрести или
добиться".
Следует
отметить еще
одно важное
обстоятельство.
В
информатике
существовали
и существуют
как бы два программирования:
теоретическое
и практическое.
Естественно,
без
теоретического
программирования
не было бы
практического,
но если
строго
следовать
первому, то
любую часть
программы
следует
строить математическими
методами,
доказывая
правильность
ее работы.
Вопросы
взаимного
влияния этих
подходов —
предмет
отдельного
обсуждения. В
данном
учебнике
речь идет в
основном о
практическом
программировании.
Однако
следует
отметить, что
теоретическое
программирование
оказывает
очень
большое
влияние на становление
и развитие
технологий
практического
программирования.
Подведем
итог.
Структурная
технология
предоставила
в
распоряжение
разработчиков
строгие
формализованные
методы
описания
программ и
принимаемых
технических
решений. При
этом
использовалась
наглядная
графическая
техника
(схемы,
диаграммы).
Однако труд
этот не был
автоматизирован,
а вручную
невозможно
было
разработать и
графически
представить
строгие
формальные
спецификации
программы,
проверить их
полноту и
непротиворечивость
и тем более
изменить.
Программы
имели последовательную
структуру, идеи
Э. Дейкстры
были
реализованы
в полной мере,
что
определило
новый этап в
развитии технологий
программирования.
Но, несмотря
на
возможность
конструирования
структур данных
различной
сложности,
данные и
действия над
данными
по-прежнему
оставались
разделены.
Разрыв между
потребностями
практики и
возможностями
разработки
(по времени,
надежности,
возможности
внесения
изменений на
стадии
эксплуатации)
сложных программ
в пределах
данной
технологической
схемы сохранялся.
Образная
формулировка
сути этого разрыва
заключается
в том, что "мы
не знаем, как
этого
достичь, у
нас нет
инструментария
для
обеспечения
процесса
правильной
разработки
программы, но
так примерно
должна работать
эта
программа".
Продолжение следует


![]() 2. Запишите условный оператор, в котором значение переменной
с вычисляется по формуле: а + b, если а — нечетное и
а • b, если а — четное.
2. Запишите условный оператор, в котором значение переменной
с вычисляется по формуле: а + b, если а — нечетное и
а • b, если а — четное.![]() х — 12, при х > 0
х — 12, при х > 0



