Могут ли машины мыслить?
А.Тьюринг
Данный материал был подготовлен И.Долмачевым для сервера vdv.1001.ru и предоставлен им для публикации в нашей газете. В тексте имеются примечания переводчика (они вынесены в сноски) и краткие комментарии И.Долмачева (они выделены из основного текста и помечены: И.А.)
Мы надеемся, что читателям "Информатики" будет очень интересно познакомиться с этой статьей и соотнести ее со статьей А.Н. Колмогорова "Автоматы и жизнь" (см. № 44/99).
"Может ли машина мыслить?"-— едва ли не самая знаменитая статья А.Тьюринга. Даже сейчас, спустя почти 50 лет после ее написания, она, вызвавшая в свое время огромное количество как серьезных исследований, так и псевдонаучных спекуляций, нисколько не утеряла своего значения. Статья написана с юмором и иронией ("словно между строк стоят смайлики, по словам Э.Ходжеса, биографа Тьюринга), но за шутливым тоном изложения скрываются одни из самых оригинальных и глубоких идей, высказанных в уходящем веке.
"Игра в имитацию", описанная в этой статье, получила название "теста Тьюринга" (ставшего стандартным теоретическим тестом на "интеллектуальность машины"), который, помимо специалистов по кибернетике, интересовал и некоторых психиатров, усмотревших глубинный психоаналитический смысл в цели игры ("угадывание пола").
Статья была впервые опубликована в научном журнале Mind, v. 59 (1950), pp. 433—460, под названием Computing Machinery and Intelligence и перепечатана в 4-м томе "Мира математики" Аж. Р. Ньюмена {The World of Mathematics. A small library... with commentaries and notes by James R. Newman, Simon & Schuster, NY, v. 4, 1956, pp. 2099-2123), где опубликована под заголовком Can the Machine think? С этого издания был сделан русский перевод, публикуемый здесь по книге:
А.Тьюринг. Может ли машина мыслить? (С приложением статьи Аж. фон Неймана Общая и логическая теория автоматов". Пер.и примечания Ю.В. Данилова). М.: ГИФМЛ, 1960.
I. Игра в имитацию
Я собираюсь рассмотреть вопрос: могут ли машины мыслить. Но для этого нужно сначала определить смысл терминов "машина" и "мыслить". Можно было бы построить эти определения так, чтобы они по возможности лучше отражали обычное употребление этих слов, но такой подход таит в себе некоторую опасность. Дело в том, что, если мы будем выяснять значения слов "машина" и "мыслить", исследуя. как эти слова определяются обычно, нам трудно будет избежать того вывода, что значение этих слов и ответ на, вопрос "могут ли машины мыслить?" следует искать путем статистического обследования наподобие анкетного опроса, проводимого институтом Гэллапа*. Однако это нелепо. Вместо того чтобы пытаться дать такое определение, я заменю Наш вопрос другим, который тесно с ним связан и выражается словами с относительно четким смыслом.
Эта новая форма может быть описана с помощью игрй, которую мы назовем "игрой в имитацию". В этой игре участвуют три человека: мужчина (А), женщина (Б) и кто-нибудь задающий вопросы (С), которым может быть лицо любого пола. Задающий вопросы отделен от двух других участников игры стенами комнаты, в которой он находится. Цель игры для задающего вопросы состоит в том, чтобы определить, кто из двух других участников игры является мужчиной (А), а кто — женщиной (В). Он знает их под обозначениями Х и У и в конце игры говорит либо: "Х есть А и У есть В", либо: "X есть В и У есть А". Ему разрешается задавать вопросы такого, например, рода:
С: "Попрошу Х сообщить мне длину его (или ее) волос".
Допустим теперь, что в действительности Х есть А. В таком случае А и должен давать ответ. Для А цель игры состоит в том, чтобы побудить С прийти к неверному заключению. Поэтому его ответ может быть, например, таким:
"Мои волосы коротко острижены, а самые длинные пряди имеют около девяти дюймов в длину".
Чтобы задающий вопросы не мог определить по голосу, кто из двух других участников игры мужчина, а кто — женщина, ответы на вопросы следовало бы давать в письменном виде, а еще лучше — на пишущей машинке. Идеальным случаем было бы телеграфное сообщение между двумя комнатами, где находятся участники игры. Если же этого сделать нельзя, то ответы и вопросы должен передавать какой-нибудь посредник. Цель игры для третьего игрока — женщины (В) — состоит в том, чтобы помочь задающему вопросы. Для нее, вероятно, лучшая стратегия — давать правдивые ответы. Она также может делать такие замечания, как "Женщина — я, не слушай- -те его!", но этим она ничего не достигнет, так как мужчина тоже может делать подобные замечания.
Поставим теперь вопрос: "Что произойдет, если в этой игре вместо А будет участвовать машина?" Будет ли в этом случае задающий вопросы ошибаться столь же часто, как и в игре, где участниками являются только люди? Эти вопросы и заменят наш первоначальный вопрос "могут ли машины мыслить?".
II. Критика новой постановки проблемы
Подобно тому как мы задаем вопрос: "В чем состоит ответ на проблему в ее новой форме?", можно спросить:
"Заслуживает ли рассмотрения проблема в ее новой постановке?". Этот последний вопрос мы рассмотрим, не откладывая дела в долгий ящик, с тем чтобы в последующем уже не возвращаться к нему.
Новая постановка нашей проблемы имеет то преимущество, что позволяет провести четкое разграничение между физическими и умственными возможностями человека. Ни один инженер или химик не претендует на создание материала, который было бы невозможно отличить от человеческой кожи. Такое изобретение, быть может, когда-нибудь будет сделано. Но даже допустив возможность создания материала, не отличимого от человеческой кожи, мы все же чувствуем, что вряд ли имеет смысл стараться придать "мыслящей машине" большее сходство с человеком, одевая ее в такую искусственную плоть. Форма, которую мы придали проблеме, отражает это обстоятельство в условии, не позволяющем задающему вопросы соприкасаться с другими участниками игры, видеть их или слышать их голоса. Некоторые другие преимущества введенного критерия можно показать, если привести образчики возможных вопросов и ответов. Например:
С: Напишите, пожалуйста, сонет на тему о мосте через реку Форт**.
А: Увольте меня от этого. Мне никогда не приходилось писать стихи.
С: Прибавьте 34 957 к 70 764.
А (молчит около 30 секунд, затем дает ответ): 105 621.
С: Вы играете в шахматы?
А: Да.
С: У меня только король на е8 и других фигур нет. У вас только король на еб и ладья на h1. Как вы сыграете?
А (после 15 секунд молчания): Лh8. Мат.
Нам кажется, что метод вопросов и ответов пригоден для того, чтобы охватить почти любую область человеческой деятельности, какую мы захотим ввести в рассмотрение. Мы не желаем ни ставить в вину машине ее неспособность блистать на конкурсах красоты, ни винить человека в том, что он терпит поражение в состязании с самолетом. условия игры делают эти недостатки несущественными. Отвечающие, если найдут целесообразным, могут хвастать своим обаянием, силой или храбростью, сколько им вздумается, и задающий вопросы не может требовать практических тому доказательств.
Вероятно, нашу игру можно подвергнуть критике на том основании, что в ней преимущества в значительной степени находятся на стороне машины. Если бы человек попытался притвориться машиной, то, очевидно, вид у него был бы весьма жалкий. Он сразу выдал бы себя медлительностью и неточностью при подсчетах. Кроме того, разве машина не может выполнять нечто такое, что следовало бы характеризовать как мышление, но что было бы весьма далеко от того, что делает человек? Это возражение очень веское. Но в ответ на него мы, во всяком случае, можем сказать, что если можно все-таки осуществить такую машину, которая будет удовлетворительно играть в имитацию, то относительно этого возражения особенно беспокоиться не следует.
Можно было бы заметить, что при "игре в имитацию" не исключена возможность того, что простое подражание поведению человека не окажется для машины наилучшей стратегией. Такой случай возможен, но я не думаю, чтобы он привел нас к чему-нибудь существенно новому. Во всяком случае, никто не пытался исследовать теорию нашей игры в этом направлении, и мы будем считать, что наилучшая стратегия для машины состоит в том, чтобы давать ответы, которые в соответствующей обстановке дал бы человек.
III. Машины, привлекаемые к игре
Вопрос, поставленный в разделе I, не станет совершенно точным до тех пор, пока мы не укажем, что именно следует понимать под словом "машина". Разумеется, нам бы хотелось, чтобы в игре можно было применять любой вид инженерной техники. Мы склонны также допустить возможность, что инженер или группа инженеров могут построить машину, которая будет работать, но удовлетворительного описания работы которой они не смогут дать, поскольку метод, которым они пользовались, был в основном экспериментальным [методом проб и ошибок]. Наконец, мы хотели бы исключить из категории машин людей, рожденных обычным образом. Трудно построить определение так, чтобы оно удовлетворяло этим трем условиям. Можно, например, потребовать, чтобы все конструкторы машины были одного пола, в действительности, однако, этого недостаточно, так как, по-видимому, можно вырастить законченный индивидуум из одной-единственной клетки, взятой (например) из кожи человека. Сделать это было бы подвигом биологической техники, заслуживающим самой высокой похвалы, но мы не склонны рассматривать этот случай как "построение мыслящей машины".
Сказанное наводит нас на мысль отказаться от требования, согласно которому в игре следует допускать любой вид техники. Мы еще больше склоняемся к этой мысли в силу того обстоятельства, что наш интерес к "мыслящим машинам" возник благодаря машине особого рода, обычно называемой "электронной вычислительной машиной", или "цифровой вычислительной машиной". Поэтому мы разрешаем принимать участие в нашей игре только цифровым вычислительным машинам.
На первый взгляд это ограничение кажется весьма сильным. Я постараюсь показать, что в действительности дело обстоит не так. Для этого мне придется дать краткий обзор природы и свойств этих вычислительных машин. Можно также "сказать, что отождествление машин с цифровыми вычислительными машинами — равно как и наш критерий "мышления" — должно быть признано совершенно неудовлетворительным, если (вопреки моему убеждению) кажется, что цифровые вычислительные машины не в состоянии хорошо играть в имитацию.
Целый ряд вычислительных машин уже находится в действии, и естественно возникает вопрос: "А почему бы нам, вместо того чтобы сомневаться в правильности наших рассуждений, не поставить эксперимент? Удовлетворить условиям'было бы нетрудно, В качестве задающих вопросы можно было бы использовать много различных людей, и полученные статистические данные показали бы, как часто задающим вопросы удавалось прийти к правильному заключению".
Коротко на этот вопрос можно ответить так: нас интересует не то, будут ли все цифровые вычислительные машины хорошо играть в имитацию, и не то, будут ли хорошо играть в эту игру те вычислительные машины, которыми мы располагаем в настоящее время; вопрос заключается в том, существуют ли воображаемые вычислительные машины, которые могли бы играть хорошо. Но это только краткий ответ. Ниже мы рассмотрим этот вопрос в несколько ином свете.
IV. Цифровые вычислительные машины
То, что мы имеем в виду, говоря о цифровых вычислительных машинах, можно пояснить следующим образом. Предполагается, что эти машины могут выполнять любую операцию, которую мог бы выполнить человек-вычислитель. Мы считаем, что вычислитель придерживается определенных, раз навсегда заданных правил и не имеет права ни в чем отступать от них. Мы можем также считать, что эти правила собраны в книге, которая заменяется другой, когда вычислитель приступает к новой работе. У человека-вычислителя имеется также неограниченный. запас бумаги, на которой он производит вычисления. Кроме того, он может выполнять операции сложения и умножения с помощью арифмометра — это несущественно.
Если данное выше пояснение принять за определение, то возникает угроза того, что наше рассуждение окажется движущимся в замкнутом круге. Чтобы избежать этой опасности, мы приведем перечень тех средств, с помощью которых достигается требуемый эффект. Можно считать, что цифровая вычислительная машина состоит из трех частей:
1) запоминающего устройства,
2) исполнительного устройства,
3) контролирующего устройства.
Запоминающее устройство — это склад информации. Оно соответствует бумаге, имеющейся у человека-вычислителя, независимо от того, является ли эта бумага той, на которой производятся выкладки, или той, на которой напечатана книга правил. Поскольку человек-вычислитель некоторые расчеты проводит в уме, часть запоминающего устройства машины будет соответствовать памяти вычислителя.
Исполнительное устройство — это часть машины, выполняющая разнообразные индивидуальные операции, из которых состоит вычисление. Характер этих операций изменяется от машины к машине. Обычно можно проделывать весьма громоздкие операции, например: "умножить 3 540 675 445 на 7 076 345 687", — однако на некоторых машинах можно выполнять только очень простые операции, вроде таких: "написать 0".
Мы уже упоминали, что имеющаяся у вычислителя "книга правил" заменяется в машине некоторой частью запоминающего устройства, которая в этом случае называется "таблицей команд". Обязанность контролирующего устройства — следить за тем, чтобы эти команды выполнялись безошибочно и в правильном порядке. Контролирующее устройство сконструировано так, что это происходит непременно.
Информация, хранящаяся в запоминающем устройстве, разбивается на небольшие части, которые распределяются по ячейкам памяти. Например, для некоторых машин такая ячейка может состоять из десяти десятичных цифр. Тем ячейкам, в которых хранится различная информация, в некотором определенном порядке приписывают номера. Типичная команда может гласить: .
"Число, хранящееся в ячейке 6809, прибавить к числу, хранящемуся в ячейке 4302, а результат поместить в ту ячейку, где хранилось последнее из чисел".
Нет необходимости говорить о том, что если все это выразить на русском [английском] языке, то машина не выполнит такую команду. Более удобно бьло бы закодировать эту команду в виде, например, числа б 809 430 217. Здесь 17 говорит о том, какую из различных операций, из тех, что можно выполнять с помощью данной машины, следует проделать с числами, хранящимися в указанных ячейках. В данном случае имеется в виду описанная выше операция, т.е. операция "число... прибавить к числу...". Следует заметить, что сама команда занимает 10 цифр и, таким образом, заполняет одну ячейку памяти, что весьма удобно. Обычно контролирующее устройство выбирает необходимые команды в том порядке, в котором они расположены, но иногда могут встречаться и такие команды:
"Теперь выполнить команду, хранящуюся в ячейке 5606, и продолжать оттуда" или же:
"Если ячейка 4505 содержит 0, выполнить команду, содержащуюся в ячейке 6707, в противном случае продолжать по порядку".
Команды этих последних типов очень важны, так как они позволяют повторять снова и снова некоторую последовательность операций до тех пор, пока не будет выполнено определенное условие, причем для повторения данной последовательности операций не приходится прибегать к новым командам. Машина просто выполняет вновь и вновь одни и те же команды. Воспользуемся аналогией из повседневной жизни. Допустим, что мама хочет, чтобы Томми по дороге в школу заходил каждое утро к сапожнику, для того чтобы справиться, не готовы ли ее туфли. Она может каждое утро снова и снова просить его об этом. Но она может также раз и навсегда повесить в прихожей записку, которую Томми будет видеть, уходя в школу, и которая будет напоминать ему о том, чтобы он зашел за туфлями. Когда Томми принесет туфли от сапожника, мама должна разорвать записку.
Читатель должен считать твердо установленным, что цифровые вычислительные машины можно строить на основе тех принципов, о которых мы рассказали выше, и что их действительно строят, придерживаясь этих принципов. Ему должно быть ясно, что цифровые вычислительные машины могут в действительности весьма точно подражать действиям человека-вычислителя.
Разумеется, описанная нами книга правил, которой пользуется вычислитель, является всего лишь удобной фикцией. На самом деле настоящие вычислители помнят, что они должны делать. Если мы хотим построить машину, подражающую действиям человека-вычислителя при выполнении некоторой сложной операции, то следует спросить последнего, как он выполняет эту операцию, и ответ представить в виде таблицы команд.
Составление таблицы команд обычно называют "программированием". "Запрограммировать выполнение машинной операции А" — значит ввести в машину подходящую таблицу команд, следуя которым машина может выполнить операцию А.
Интересной разновидностью цифровых вычислительных машин являются "цифровые вычислительные машины со случайным элементом". Такие машины имеют команды, содержащие бросание игральной кости или какой-нибудь эквивалентный электронный процесс. Одной из таких команд может быть, например, следующая: "бросить кость и полученное при бросании число поместить в ячейку 1000". Иногда говорят, что такие машины обладают свободой выбора (хотя лично я не стал бы употреблять такое выражение) . Установить наличие "случайного элемента" в машине путем наблюдений за ее действием обычно оказывается невозможным, так как если сделать, например, выбор команды зависимым от последовательности цифр в десятичном разложении числа р, то результат получится совершенно аналогичный.
Все существующие в действительности цифровые вычислительные машины обладают лишь конечной памятью. Однако теоретически нетрудно представить себе машину с неограниченной памятью. Разумеется, в любой данный момент времени возможно использование только конечной части запоминающего устройства. Точно так же запоминающее устройство, которое можно физически осуществить, всегда имеет конечные размеры, но мы можем представлять дело так, что по мере надобности к нему пристраиваются все новые и новые части. Такие вычислительные машины представляют особый теоретический интерес, и впредь мы будем их называть машинами с бесконечной емкостью памяти.
Сама идея цифровой вычислительной машины отнюдь не является новой. Чарлз Бэббидж*, занимавший с 1828-го по 1839 г. Люкасовскую кафедру по математике в Кембридже*, разработал проект вычислительного устройства, названного им "Аналитической машиной"; создание ее, однако, так и не удалось завершить. Хотя у Бэббиджа были все основные идеи, существенные для создания такого механизма, его машина не имела перспектив. Скорость вычислений, которую позволила бы достичь машина Бэббиджа, оказалась бы, разумеется, выше скорости, достигаемой человеком, однако она была бы почти в 100 раз меньше, чем у той вычислительной машины, которая в настоящее время работает в Манчестере* и которая является одной из самых медленных современных машин. Запоминающее устройство в машине Бэббиджа было задумано как чисто механическое, с использованием карт и зубчатых колес.
То, что Аналитическая машина Бэббиджа была задумана как чисто механический аппарат, помогает нам избавиться от одного предрассудка. Часто придают значение тому обстоятельству, что современные цифровые машины являются электрическими устройствами и что нервную систему человека в некотором смысле можно отождествить с электрическим устройством. Но, поскольку машина Бэббиджа не была электрическим аппаратом и поскольку в известном смысле все цифровые вычислительные машины эквивалентны, становится ясно, что использование электричества в этом случае не может иметь теоретического значения. Естественно, что там, где требуется быстрая передача сигналов, обычно появляется электричество, поэтому неудивительно, что мы встречаем его в обоих указанных случаях. Для нервной системы химические явления играют по крайней мере столь же важную роль, что и электрические. В некоторых же вычислительных машинах запоминающее устройство в основном акустическое. Отсюда ясно, что сходство между нервной системой и цифровыми вычислительными машинами, состоящее в том, что в обоих случаях используется электричество, сводится лишь к весьма поверхностной аналогии. Если мы действительно хотим открыть глубокие связи, нам скорее следует искать сходство в математических моделях функционирования нервной системы и цифровых вычислительных машин.
V. Универсальность цифровых вычислительных машин
Рассмотренные в предыдущем разделе цифровые вычислительные машины можно отнести к классу "машин с дискретными состояниями". Так называются машины, работа которых складывается из совершающихся последовательно одна за другой резких смен их состояния. Состояния, о которых идет речь, достаточно отличаются друг от друга, поэтому можно пренебречь возможностью принять по ошибке одно из них за другое. Строго говоря, таких машин не существует. В действительности всякое движение непрерывно. Однако имеется много видов машин, которые удобно считать машинами с дискретными состояниями.
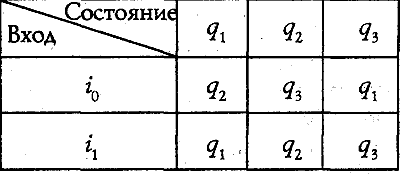
Например, если рассматривать выключатели осветительной сети, то удобно считать, отвлекаясь от действительного положения дела, что каждый выключатель может быть либо включён, либо выключен. То, что выключатель фактически имеет также и промежуточные состояния, несущественно для наших целей, и мы можем об этом забыть. Приведу пример машины с дискретными состояниями. Рассмотрим колесико, способное через каждую секунду совершать скачкообразный поворот (щелчок) на 120°, но которое можно застопоривать с помощью рычажка, управляемого извне. Пусть, кроме того, в момент, когда колесико принимает какое-нибудь определенное положение (одно из трех возможных для него), загорается лампочка. В абстрактном виде эта машина выглядит так. Внутреннее состояние машины (которое задается положением колесика) может быть q1, q2 или q3. На вход машины подается либо сигнал i0 либо сигнал i1 (положения рычажка). Внутреннее состояние в любой момент определено предыдущим состоянием и сигналом на входе согласно следующей таблице:

Сигналы на выходе, единственно видимые извне проявления внутреннего состояния (загорание лампочки), задаются таблицей
Состояние |
q1 | q2 | q3 |
| Выход | o1 | o2 | o3 |
Этот пример типичен для машин с дискретными состояниями. Такие машины можно описывать с помощью таблиц при условии, что они обладают конечным числом возможных состояний.
Очевидно, что при заданном начальном состоянии машины и заданном сигнале на входе всегда возможно предсказать все будущие состояния. Это напоминает точку зрения Лапласа, утверждавшего, что если известны положения и скорости всех частиц во Вселенной в некоторый момент времени, то из такого полного описания ее состояния можно предсказать все ее будущие состояния. Однако то предсказание будущего, о котором у нас идет речь, гораздо ближе к практическому осуществлению, чем то, которое имел в виду Лаплас. Система "Вселенной как единого целого" такова, что даже очень небольшие отклонения в начальных состояниях могут иметь решающее значение в последующем. Смещение одного электрона на одну миллиардную долю сантиметра в некоторый момент времени может явиться причиной того, что через год человек будет убит обвалом в горах. Существенной особенностью тех механических систем, которые мы назвали "машинами с дискретными состояниями", является то, что в них это явление не имеет места. Даже если вместо идеализированных машин взять реальные физические машины, то точное (в разумных пределах) знание о состоянии машины в один момент времени позволяет нам с разумной степенью точности предсказать любое число ее состояний в последующем.
Как мы уже упоминали, цифровые вычислительные машины относятся к классу машин с дискретными состояниями. Но число состояний, в которых может находиться такая машина, обычно велико Например, число состояний машины, работающей в настоящее время в Манчестере, равно приблизительно 2165000, т.е. почти 1050000. Сравните эту величину с числом состояний описанного выше "щелкающего" колесика. Нетрудно понять, почему число состояний вычислительной машины оказывается столь огромным. В вычислительной машине имеется запоминающее устройство, соответствующее бумаге, которой пользуется человек-вычислитель. Запоминающее устройство должно быть таково, чтобы в нем можно было записать любую комбинацию символов, которая может быть написана на бумаге Для простоты допустим, что в качестве символов используются только цифры от 0 до 9. Различия в почерках не принимаются во внимание. Допустим, что человек-вычислитель располагает 100 листами бумаги, разграфленными на 50 строк каждый Строка может вместить 30 цифр. Число состояний в этом случае равно 10100· 50·30, т.е. 10150000. Это приблизительно равно числу состояний трех Манчестерских машин, взятых вместе. Логарифм числа состояний по основанию 2 обычно называют "емкостью памяти" машины. Например, Манчестерская машина обладает емкостью памяти около 165 000, а машина с колесиком из нашего примера — около 1,6. Если две машины соединены вместе, то емкость памяти объединенной машины представляет собой сумму емкостей памяти составляющих машин. Это позволяет формулировать такие утверждения, как "Манчестерская машина содержит 64 магнитных трека (направляющих приспособлений), каждый емкостью по 2560, восемь электронно-лучевых трубок емкостью по 1280. Число различных запоминающих устройств доходит до 300, что в целом приводит к емкости памяти в 174 380 единиц"*
Таким образом, емкость памяти 100 листов бумаги (разграфленных на 50 строк каждый, где каждая строка может вместить 30 цифр), о которых говорит Тьюринг, составляет примерно 61 килобайт, а емкость памяти Манчестерской машины составляла примерно 20 килобайт. — Прим И. Д.
Если задана таблица, соответствующая некоторой машине с дискретными состояниями, то можно предсказать, что будет делать эта машина. Нет причин, по которым эти вычисления не могли бы выполняться с помощью цифровой вычислительной машины. Если бы с помощью цифровой вычислительной машины можно было достаточно быстро производить вычисления, то ее можно было бы использовать для имитации поведения любой машины с дискретными состояниями. В "игре в имитацию" тогда могли бы участвовать машина с дискретными состояниями (которая играла бы за В) и имитирующая ее цифровая вычислительная машина (в качестве А), и задающий вопросы не смог бы отличить их друг от друга. Разумеется, для этого необходимо, чтобы цифровая вычислительная машина имела надлежащую емкость памяти, а также работала достаточно быстро. Кроме того, ее пришлось бы снабжать новой программой для каждой новой машины, которую она должна была бы имитировать.
Именно это особое свойство цифровых вычислительных машин — то, что они могут имитировать любую машину с дискретными состояниями, и имеют в виду, когда говорят, что цифровые вычислительные машины являются универсальными машинами. Из того, что имеются машины, обладающие свойством универсальности, вытекает важное следствие: чтобы выполнять различные вычислительные процедуры, нам вовсе не нужно создавать все новые и новые разнообразные машины (если отвлечься от растущих требований к быстроте вычислений) Все вычисления могут быть выполнены с помощью одной-единственной цифровой вычислительной машины, если снабжать ее надлежащей программой для каждого случая. В дальнейшем мы увидим в качестве следствия из этого результата, что все цифровые вычислительные машины в каком-то смысле эквивалентны друг другу.
Теперь мы можем вернуться к вопросу, поднятому нами в конце раздела III. Там мы высказали предположение, что вопрос "могут ли машины мыслить?" можно заменить вопросом "существуют ли воображаемые цифровые вычислительные машины, которые могли бы хорошо играть в имитацию?". Если угодно, мы можем придать этому вопросу видимость большей общности и спросить: "Существуют ли машины с дискретными состояниями, которые могли бы хорошо играть в эту игру?" Но в свете того, что цифровые вычислительные машины универсальны, мы видим, что любой из таких вопросов эквивалентен следующему: "Если взять только одну конкретную цифровую вычислительную машину Ц, то спрашивается: справедливо ли утверждение о том, что, изменяя емкость памяти этой машины, увеличивая скорость ее действия и снабжая ее подходящей программой, можно заставить Ц удовлетворительно исполнять роль А в "игре в имитацию" (причем роль В будет исполнять человек).
VI. Противоположные точки зрения по основному вопросу
Теперь мы можем считать, что основные понятия нами выяснены, и перейти к рассмотрению вопроса "могут ли машины мыслить?" и его варианта, изложенного в конце предыдущего раздела. Вместе с тем мы не можем отказаться от первоначальной формы вопроса, так как по поводу равноценности замены одной формы вопроса другой мнения могут расходиться и в любом случае необходимо выслушать то, что было бы сказано в этой связи.
Читателю будет легче разобраться в этой дискуссии, если я сначала разъясню свои собственные убеждения. Рассмотрим сперва более точную форму вопроса. Я уверен, что через пятьдесят лет станет возможным программировать работу машин с емкостью памяти около 106 так, чтобы они могли играть в имитацию настолько успешно, что шансы среднего человека установить присутствие машины через пять минут после того, как он начнет задавать вопросы, не поднимались бы выше 70%. Первоначальный вопрос "могут ли машины мыслить?" я считаю слишком неосмысленным, чтобы он заслуживал рассмотрения. Тем не менее я убежден, что к концу нашего века употребление слов и мнения, разделяемые большинством образованных людей, изменятся настолько, что можно будет говорить о мыслящих машинах, не боясь, что тебя поймут неправильно. Более того, я считаю вредным скрывать такие убеждения. Широко распространенное представление о том, что ученые с неуклонной последовательностью переходят от одного вполне установленного факта к другому, не менее хорошо установленному факту, не давая увлечь себя никакому непроверенному предположению, в корне ошибочно. Не будет никакого ущерба от того, что мы ясно осознаем, что является доказанным фактом, а что предположением. Догадки очень важны, ибо они подсказывают направления, полезные для исследований.
Теперь я перехожу к рассмотрению мнений, противоположных моему собственному.
1. Теологическое возражение
"Мышление есть свойство бессмертной души человека, Бог дал бессмертную душу каждому мужчине и каждой женщине, но не дал души никакому другому животному и машинам. Следовательно, ни животное, ни машина не могут мыслить"*.
Я не могу согласиться ни с чем из того, что было только что сказано, и попробую возразить, пользуясь теологическими же терминами. Я счел бы данное возражение более убедительным, если бы животные были отнесены в один класс с людьми, ибо, на мой взгляд, между типичным одушевленным и типичным неодушевленным предметами имеется большее различие, чем между человеком и другими животными. Произвольный характер этой ортодоксальной точки зрения станет еще яснее, если мы рассмотрим, в каком свете она может представиться человеку, исповедующему какую-нибудь другую религию. Как, например, христиане отнесутся к точке зрения мусульман, считающих, что у женщин нет души? Но оставим этот вопрос и обратимся к основному возражению. Мне кажется, что из приведенного выше аргумента со ссылкою на душу у человека следует серьезное ограничение всесильности Всемогущего. Пусть даже существуют определенные вещи, которые Бог не может выполнить, — например, сделать так, чтобы единица оказалась равной двум; но кто же из верующих не согласился бы с тем, что Он волен вселить душу в слона, если найдет, что слон этого заслуживает? Мы можем искать выход в предположении, что Он пользуется своей силой лишь в сочетании с мутациями, совершенствующими мозг настолько, что последний оказывается в состоянии удовлетворить требованиям души, которую Он желает вселить в слона. Но точно так же можно рассуждать и в случае машин. Это рассуждение может показаться отличным лишь. потому, что в случае машин его труднее "переварить". По сути дела это означает, что мы считаем весьма маловероятным, чтобы Бог счел обстоятельства подходящими для того, чтобы дать душу машине, т.е. речь идет в действительности о других аргументах, которые обсуждаются в остальной части статьи. Пытаясь построить мыслящие машины, мы поступаем по отношению к Богу более непочтительно, узурпируя Его способность создавать души, чем мы делаем это, производя потомство; в обоих случаях мы являемся лишь орудиями его воли и производим лишь убежища для душ, которые творит опять-таки Бог.
Все это, однако, пустые рассуждения. В пользу чего бы ни приводили такого рода теологические доводы, они не производят на меня особого впечатления. Однако в старину такие аргументы находили весьма убедительными. Во времена Галилея полагали, что такие церковные тексты, как "Стояло солнце среди неба и не спешило к западу почти целый день" (Иисус Навин, 10, 3) и "Ты поставил землю на твердых основах; не поколеблется она в веки и веки" (псалом 103, 5), в достаточной мере опровергали теорию Коперника. В наше время такого рода доказательство представляется беспочвенным. Но, когда современный уровень знаний еще не был достигнут, подобные доводы производили совсем другое впечатление.
2. Возражение со "страусиной" точки зрения [The "Heads in the Sand" Objection]
"Последствия машинного мышления были бы слишком ужасны. Будем надеяться и верить, что машины не могут мыслить".
Это возражение редко выражают в столь открытой форме. Но оно звучит убедительно для большинства из тех, кому оно вообще приходит в голову. Мы склонны верить, что человек в интеллектуальном отношении стоит выше всей остальной природы. Лучше всего, если бы удалось доказать, что человек необходимо является самым совершенным существом, ибо в таком случае он может бояться потерять свое доминирующее положение. Ясно, что популярность теологического возражения связана именно с этим чувством. Это чувство, вероятно, особенно сильно у людей интеллигентных, так как они ценят силу мышления выше, чем остальные люди, и более склонны основывать свою веру в превосходство человека на этой способности.
Я не считаю, что это возражение является достаточно существенным для того, чтобы требовалось какое-либо опровержение. Утешение здесь было бы более подходящим; не предложить ли искать его в учении о переселении душ?
3. Математическое возражение
Имеется ряд результатов математической логики, которые можно использовать для того, чтобы показать наличие определенных ограничений возможностей машин с дискретными состояниями. Наиболее известный из этих результатов — теорема Гёделя* — показывает, что в любой достаточно мощной логической системе можно сформулировать такие утверждения, которые внутри этой системы нельзя ни доказать, ни опровергнуть, если только сама система непротиворечива. Имеются и другие, в некотором отношении аналогичные, результаты, принадлежащие Черчу, Клини, Россеру и Тьюрингу*. Результат последнего особенно удобен для нас, так как относится непосредственно к машинам, в то время как другие результаты можно использовать лишь как сравнительно косвенный аргумент (например, если бы мы стали опираться на теорему Гёделя, нам понадобились бы еще и некоторые средства описания логических систем в терминах машин и машин в терминах логических систем). Результат Тьюринга относится к такой машине, которая, в сущности, является цифровой вычислительной машиной с неограничейной емкостью памяти, и устанавливает, что существуют определенные вещи, которые эта машина не может выполнить. Если она устроена так, чтобы давать ответы на вопросы, как в "игре в имитацию", то будут вопросы, на которые она или даст неверный ответ, или не сможет дать ответа вообще, сколько бы ни было ей предоставлено для этого времени. Таких вопросов, конечно, может быть много, и на вопросы, на которые нельзя получить ответ от одной машины, можно получить удовлетворительный ответ от другой. Мы здесь, разумеется, предполагаем, что вопросы принадлежат скорее к таким, которые допускают ответ "да" или "нет", чем к таким, как: "Что вы думаете о Пикассо?". Следующего типа вопросы относятся к числу таких, на которые, как нам известно, машина не может дать ответ: "Рассмотрим машину, характеризующуюся следующим: ...Будет ли эта машина всегда отвечать "да" на любой вопрос?" Если на место точек поставить описание (в какой-либо стандартной форме, например, подобной той, которая была использована нами в разделе V) такой машины, которая находится в некотором сравнительно простом отношении к машине, к которой мы обращаемся с нашим вопросом, то можно показать, что ответ на этот вопрос окажется либо неверным, либо его вовсе не будет. В этом и состоит математический результат*; утверждают, будто он доказывает ограниченность возможностей машин, которая не присуща разуму человека.
А для тех любознательных компьютерщиков, которые, возможно, не поверили на слово, что такую программу U нельзя написать, поясню, опуская детали (к которым можно придраться, но они все же несущественны), в чем тут дело. Если бы такая программа U была написана, то ее можно было бы легко переделать так, чтобы вместо команды вывода изображения девушки на экран она бы зацикливалась (вставить для этого, скажем, "вечный цикл" for(„); ). Пусть эта переделанная программа называется U2. Что будет делать программа U2, если ей на вход подать текст программы U2 (текст себя самой) ? Если она зацикливается, то она должна показать фотографию юноши и остановиться, т.е. не зациклиться. Но если она не зацикливается, это значит, что она должна зациклиться (поскольку вывод девушки в программе U был заменен на "вечный цикл"). Тем самым программа U2 оказывается в безвыходном положении, несовместимом с допущением возможности ее существования. — Прим. И.Д.
Ответ на это возражение вкратце состоит в следующем. Установлено, что возможности любой конкретной машины ограничены, однако в разбираемом возражении содержится голословное, без какого бы то ни было доказательства, утверждение, что подобные ограничения не применимы к разуму человека. Я не думаю, чтобы можно было так легко игнорировать эту сторону дела. Когда какой-либо из такого рода машин задают соответствующий критический вопрос и она дает определенный ответ, мы заранее знаем, что ответ будет неверным, и это дает нам чувство известного превосходства., Не является ли это чувство иллюзорным? Несомненно, оно бывает довольно искренним, но я не думаю, чтобы ему следовало придавать слишком большое значение. Мы сами слишком часто даем неверные ответы на вопросы, чтобы то чувство удовлетворения, которое возникает у нас при виде погрешимости машин, имело оправдание. Кроме того, чувство превосходства может относиться лишь к машине, над которой мы одержали свою — в сущности весьма скромную — победу. Не может быть и речи об одновременном торжестве над всеми машинами. Значит, короче говоря, для любой отдельной машины могут найтись люди, которые умнее ее, однако в этом случае снова могут найтись другие, еще более умные машины, и т.д.
Я думаю, что те, кто разделяет точку зрения, выраженную в математическом возражении, как правило, охотно примут "игру в имитацию" в качестве основы дальнейшего рассмотрения. Те же, кто убежден в справедливости двух предыдущих возражений, будут, вероятно, вообще не заинтересованы ни в каком критерии.
4. Возражение с точки зрения сознания [The Argument from Consciousness]
Это возражение особенно ярко выражено в выступлении профессора Джефферсона* на Листеровских чтениях за 1949 год*, откуда я и привожу цитату. "До тех пор, пока машина не сможет написать сонет или сочинить музыкальное произведение, побуждаемая к тому собственными мыслями и эмоциями, а не за счет случайного совпадения символов, мы не можем согласиться с тем, что она равносильна мозгу, т.е. что она может не только написать эти вещи, но и понять то, что ею написано. Ни один механизм не может чувствовать (а не просто искусственно сигналить, для чего требуется достаточно несложное устройство) радость от своих успехов, горе от постигших его неудач, удовольствие от лести, огорчение из-за совершенной ошибки, не может быть очарованным противоположным полом, не может сердиться или быть удрученным, если ему не удается добиться желаемого".
Это рассуждение, по-видимому, означает отрицание нашего критерия. Согласно самой крайней форме этого взгляда, единственный способ, с помощью которого можно удостовериться в том, что машина может мыслить, состоит в том, чтобы стать машиной и осознавать процесс собственного мышления. Свои переживания можно было бы потом описать другим, но, конечно, подобное сообщение никого бы не удовлетворило. Точно так же, если следовать этому взгляду, то окажется, что единственный способ убедиться в том, что данный человек действительно мыслит, состоит в том, чтобы стать именно этим человеком. Фактически эта точка зрения является солипсистской*. Быть может, подобные воззрения весьма логичны, но если исходить из них, то обмен идеями становится весьма затруднительным. Согласно этой точке зрения, А обязан думать, что "А мыслит, а В нет", в то время как В убежден в том, что "В мыслит, а А нет". Вместо того чтобы постоянно спорить по этому вопросу, обычно принимают вежливое соглашение о том, что мыслят все.
В русском издании статьи "Может ли машина мыслить?" к этому примечанию добавлено еще одно предложение: "Солипсизм есть крайняя форма философии субъективного идеализма". Школьная форма солипсического credo, высказываемая иногда наиболее продвинутыми учащимися на уроках обществоведения, звучит примерно так: "Вы все существуете лишь в моем воображении, реален лишь я вместе с моими чувствами и ощущениями". Между тем великий философ Людвиг Витгенштейн (1889—1951), чьи лекции по философии математики в Кембридже посещал Тьюринг, заметил как-то: "Здесь мы можем видеть, что солипсизм совпадает с чистым реализмом, если он строго продуман". Эти слова Витгенштейна были выбраны в качестве эпиграфа к рассказу известного современного писателя Виктора Пелевина "Девятый сон Веры Павловны" и определили его содержание; см. напр.: Викшор Пелевин. Синий фонарь. М.: "Текст", 1991. — Прим. И.Д.
Я уверен, что профессор Джефферсон отнюдь не желает стоять на этой крайней солипсистской точке зрения. Вероятно, он весьма охотно принял бы в качестве критерия "игру в имитацию". Эта, игра (если игрок В не участвует) нередко применяется на практике под названием viva voce (устно) для того, чтобы установить, понял ли действительно данный человек некоторую вещь, или он заучил нечто, как попугай. Вот отрывок из такой игры.
Задающий вопросы: Не находите ли Вы, что в первой строке Вашего сонета: "Сравню ль тебя я с летним днем" выражение "с весенним днем" звучало бы лучше?
Отвечающий: Оно нарушало бы размер стиха.
Задающий вопросы: А если сказать "с зимним днем" ? С размером здесь все обстоит благополучно.
Отвечающий: Это так, но никто не захочет, чтобы его сравнивали с зимним днем.
Задающий вопросы: А разве мистер Пиквик не напоминает Вам Рождество?
Отвечающий: Некоторым образом да.
Задающий вопросы: Но Рождество — зимний день, и я не думаю, чтобы мистер Пиквик имел что-нибудь против этого сравнения.
Отвечающий: Я не думаю, что вы говорите все это всерьез. Когда говорят о зимнем дне, имеют в виду обычно зимний день, а не какой-то особенный, вроде Рождества.
И так далее. Что бы сказал профессор Джефферсон, если бы машина, пишущая сонеты, могла отвечать примерно так, как это было в приведенном выше отрывке из viva voce. He знаю, стал ли бы он рассматривать ответы машины лишь как "просто искусственную сигнализацию". Если бы ее ответы были столь же связными и удовлетворительными по содержанию, как в приведенном выше отрывке, я не думаю, чтобы профессор Джефферсон охарактеризовал это как дело, выполнить которое может "достаточно несложное устройство". Эту фразу из его выступления следует, по-видимому, относить к таким случаям, когда в машине имеется, скажем, граммофонная пластинка с записью сонета в чьем-либо исполнении, а также механизм, с помощью которого эту запись можно время от времени включать.
Короче говоря, я считаю, что большинство из тех, кто поддерживает возражение с точки зрения сознания [consciousness], скорее откажутся от своих взглядов, чем признают солипсистскую точку зрения. В таком случае они, по-видимому, охотно примут наш критерий.
Мне не хотелось бы создавать впечатление, будто я считаю, что в сознании нет ничего загадочного. Например, неудача наших попыток локализовать сознание похожа на парадокс. Но я вовсе не думаю, что загадки, связанные с сознанием, непременно должны быть разъяснены прежде, чем мы окажемся в состоянии ответить на вопрос, рассматриваемый в настоящей статье.
5. Возражения, исходящие из того, что машина не все может выполнить [Arguments from Various Disabilities]
Обычно эти возражения выражают в такой форме: "Я согласен с тем, что вы можете заставить машины делать все, о чем вы упоминали, но вам никогда не удастся заставить их делать X". При этом перечисляют довольно длинный список значений этого X. Я предлагаю читателю выбирать: "Быть добрым, находчивым, красивым, дружелюбным, быть инициативным, обладать чувством юмора, отличать правильное от неправильного, совершать ошибки, влюбляться, получать удовольствие от клубники со сливками, заставить кого-нибудь полюбить себя, извлекать уроки из своего опыта, правильно употреблять слова, думать о себе, обладать таким же разнообразием в поведении, каким обладает человек, создавать нечто подлинно новое".
Обычно в подтверждение подобных высказываний не приводят никаких доводов. Я убежден, что эти высказывания основываются главным образом на принципе неполной индукции*. Человек в течение своей жизни видел тысячи машин. Из того, что он видел, он делает ряд общих заключений. Машины безобразны, каждая из них создана для того, чтобы выполнять весьма ограниченные задачи, если необходимо сделать нечто иное, они бесполезны, вариации их поведения крайне незначительны и т.д. и т.п. Естественно, человек делает вывод, что все это является необходимыми особенностями всех машин в целом. Многие из этих ограничений связаны с очень маленькой емкостью памяти большинства машин. (При этом я предполагаю, что понятие емкости памяти машины несколько обобщено таким образом, что охватывает и машины, отличные от машин с дискретными состояниями. Точное определение не играет здесь никакой роли, так как в настоящем рассмотрении мы не претендуем на математическую строгость.) Несколько лет назад, когда очень немногие знали о цифровых вычислительных машинах, часто приходилось встречаться с недоверчивым отношением к тому, что о них рассказывали, если об их замечательных свойствах говорили, не объясняя, как такие машины устроены. Это, вероятно, происходило из-за того, что слушавшие шаблонно применяли принцип неполной индукции. Разумеется, применение этого принципа происходило в основном бессознательно. Если ребенок, обжегшись один раз, боится огня и выражает страх перед огнем тем, что избегает его, то я бы сказал, что он применяет неполную индукцию (само собой разумеется, поведение ребенка можно описать и по-другому), Я не думаю, чтобы трудовая деятельность и обычаи человечества были особенно удачным материалом для применения неполной индукции. Большую часть пространственно-временного континуума [space-time} необходимо пытливо исследовать, если мы хотим получить надежные результаты. В противном случае мы можем прийти, скажем, к выводу (к которому приходит большинство английских детей), что все говорят по-английски и что глупо изучать французский язык.
Выражение "неполная индукция" русского перевода соответствует выражению "scientific induction" (буквально: "научная индукция") английского оригинала. Такой перевод выбран потому, что выражение "научная индукция" употребляется у нас обычно не в том смысле, который имеет в статье Тьюринга выражение "scientific induction" (под "научной индукцией" в нашей литературе обычно понимают сложное рассуждение, основанное на совместном применении неполной индукции и дедукции, которое при определенных условиях — последние, впрочем, не уточняются — может давать достоверное заключение),
Короче говоря, здесь имеется в виду то, что при индуктивном умозаключении от частного к общему мы можем получить весьма сомнительный, если вообще не абсолютно ложный вывод — как в тьюринговском примере с английскими детьми (хотя в современном мире более яркий пример явили бы собою американские дети, равно как и многие американские взрослые).
Вот еще один пример умозаключения по (неполной) индукции. "Неужели наша школа "учимся говорить публично" нужна только двадцати человекам, ...Нет, я знаю, уверен, что умение говорить нужно каждому из нас. ...Да, курс "учимся говорить публично" [...] способен помочь каждому человеку значительно улучшить свою устную речь". —Прим. И. Д.
Однако относительно многого из того, что было названо в числе вещей, недоступных машине, следует сделать особые оговорки. Неспособность машины получать удовольствие от клубники со сливками может показаться читателю пустяком. Весьма возможно даже, что мы могли бы сделать так, чтобы машина получала удовольствие от этого изысканного блюда, но любая попытка в этом направлении была бы идиотизмом. Эта неспособность машины приобретает значение лишь в сочетании с другими труднодоступными для нее вещами, например, в сочетании с трудностью установления между нею и человеком такого же отношения дружелюбия, какое бывает между двумя людьми.
Фраза в английском оригинале звучит так: "As between white man and white man, or between black man and black man" ("между белым мужчиной и белым мужчиной, или между черным мужчиной и черным мужчиной"; "man" может переводиться и как "человек", и как "мужчина"). Иными словами, переводчик здесь изрядно "закрасил" непристойную в советские времена шутку (ясно, какого рода отношения между мужчинами мог иметь в виду здесь Тьюринг, хоть он и вставил "для отвода глаз" "проблемную расовую тему". Эту неточность перевода я обнаружил совершенно случайно, и из-за нее, по всей видимости, позже придется пересмотреть весь публикуемый русский перевод, поскольку я думаю, что это далеко не единичный случай "сглаживания" игривого тона автора. — Прим. И..Д.
Утверждение "машины не могут совершать ошибок" кажется мне курьезным. Его пытаются парировать: "А разве они от этого хуже?" Отнесемся к этому утверждению не столь враждебно и попытаемся понять, что имеют в виду в действительности. Я думаю, что возражение, содержащееся в утверждении "машины не могут совершать ошибок", можно пояснить с помощью "игры в имитацию". Требуется, чтобы задающий вопросы отличил машину от человека, просто задавая им ряд арифметических задач; машина должна разоблачить себя вследствие своей высокой точности. Ответ на эту аргументацию очень прост. Можно сделать так, чтббы машина (запрограммированная для участия в игре) не стремилась давать правильные ответы на арифметические задачи. Она может в известной мере специально вводить ошибки в вычисления, для того чтобы сбить с толку задающего вопросы. Что касается ошибок, связанных с механическими неисправностями, то такие ошибки обнаружат себя, по-видимому, тем, что ошибочный результат в этом случае окажется трудно подвести под некоторый общий род типичных арифметических ошибок. Однако даже такая интерпретация данного возражения не является приемлемой. Размеры настоящей статьи не позволяют нам остановиться на этом более подробно. Мне кажется, что это возражение возникает потому, что смешивают ошибки двух родов. Их можно называть "ошибками функционирования" и "ошибками вывода". Ошибки функционирования происходят вследствие некоторых механических или электрических неисправностей, в результате которых машина ведет себя не так, как это было намечено. В философских дискуссиях обычно отвлекаются от возможности ошибок такого рода; поэтому подвергают рассмотрению "абстрактные машины". Эти абстрактные машины — математические фикции, а не реально существующие объекты. По определению, они не могут иметь ошибок функционирования. В этом смысле мы действительно можем сказать, что "машины никогда не могут ошибаться". Ошибки вывода могут возникать лишь тогда, когда сигналу на выходе машины придан определенный смысл. Например, машина может выдавать в печатном виде математические уравнения или какие-нибудь высказывания на русском (английском) языке. Если при этом печатается ложное предложение, мы говорим, что машина совершила ошибку вывода. У нас, очевидно, вовсе нет оснований для утверждения, что машина не может совершать ошибок этого рода. Например, она может только и делать, что печатать "0=1". В качестве более естественного примера рассмотрим машину, располагающую каким-то методом для того, чтобы делать заключения на основе неполной индукции. Мы должны ожидать, что такой метод в отдельных случаях будет давать ошибочные результаты.
На утверждение о том, что машина не может иметь предметом, своей мысли самое себя, можно, конечно, дать ответ лишь в том случае, если бы было возможно показать, что машина вообще имеет какие-либо мысли, выражающие какое-либо предметное содержание. Все же выражение "предметное содержание машинных операций" имеет некоторый смысл, по крайней мере для тех, кто имеет дело с машинными вычислениями. Если, например, машина решает уравнение х2 — 40х — 11 == О, то уравнение можно считать частью предметного содержания операций машины в данный момент. В этом смысле содержанием операций машины, безусловно, может быть она сама. Ее можно использовать при составлении своей собственной программы или для предсказания последствий, вызываемых изменениями в ее устройстве. Наблюдая результаты своего поведения, машина сможет изменять свои собственные программы с тем, чтобы быть более эффективной в достижений некоторой цели. Все это станет возможно в ближайшем будущем; это не утопические мечты.
К сожалению, публикуя статью Тьюринга на страницах газеты, нет возможности даже в краткой степени пояснить, насколько верно здесь Тьюринг смотрел в будущее. — Прим. И.Д.
Возражение, состоящее в том, что машина не отличается разнообразием поведения, является всего лишь способом выражения того обстоятельства, что она не обладает большой емкостью памяти. До самого последнего времени емкость памяти даже в тысячу цифр была очень редкой.
Все возражения, которые мы сейчас разбираем, часто являются просто замаскированной формой возражения с точки зрения сознания. Обычно, если утверждают, что машина может выполнить что-нибудь из того, что было перечислено в начале раздела 5, и при этом описывают сущность метода, которым пользуется машина, это не производит большого впечатления. Считают, что, в чем бы ни состоял этот метод, он должен быть весьма элементарным, так как носит механический характер. Сравните сказанное с тем, что говорит Джефферсон (см. эту ссылку).
6. Возражение леди Лавлейс
Наиболее подробные сведения, которыми мы располагаем об Аналитической машине Бэббиджа, берутся из воспоминаний леди Лавлейс*. В них она высказывает такую мысль: "Аналитическая машина не претендует на то, чтобы создавать что-то действительно новое. Машина может выполнить все то, что мы умеем ей предписать" (курсив леди Лавлейс). Это высказывание цитируется Хартри*, который добавляет: "Отсюда не следует, что невозможно сконструировать электронное устройство, которое "мыслит", или в котором, пользуясь биологическими терминами, можно вырабатывать условные рефлексы, на основе которых становится возможным "обучение". Увлекательный и будирующий вопрос, подсказанный некоторыми из последних достижений, состоит в том, осуществимо это принципиально или нет. Однако не видно, чтобы машины, построенные или запроектированные до настоящего времени, обладали этим свойством".
Я полностью согласен с Хартри по этому вопросу. Следует отметить, что он вовсе не утверждает в категорической форме, что машины, о которых идет речь, не обладают этим свойством. Он лишь замечает, что данные, которыми располагала госпожа Лавлейс, не позволяли ей допустить этого. Весьма возможно, что машины, о которых шла речь, в некотором смысле обладали этим свойством. Действительно, пусть некоторая машина с дискретными состояниями обладает рассматриваемым свойством. Аналитическая машина Бэббиджа была универсальной цифровой вычислительной машиной; это значит, что если бы она обладала нужной емкостью памяти и необходимой скоростью работы, то, будь в нее введена соответствующая программа, она могла бы подражать этой машине. По-видимому, этот довод не приходил в голову ни Бэббиджу, ни графине Аавлейс. Во всяком случае, от них нельзя требовать, чтобы они исчерпали все, что можно сказать по этому вопросу.
Весь этот вопрос будет рассмотрен еще раз в разделе, посвященном обучающимся машинам.
Один из вариантов аргумента госпожи Лавлейс — это утверждение, гласящее, что машина "никогда не может создать ничего подлинно нового". На секунду возразим поговоркой, что вообще "ничто не ново под Луной", Кто может быть уверенным в том, что выполненная им "оригинальная работа" не была ростком из зерна, посеянного образованием, или просто результатом применения хорошо известных общих принципов. Более удачный вариант этого возражения состоит в утверждении, что "машина никогда не может ничем поразить человека". Это утверждение представляет собой прямой вызов, который, однако, мы можем принять, не уклоняясь. Лично меня машины удивляют очень часто. В основном это происходит потому, что я не могу точно рассчитать, чего можно, а чего нельзя ожидать от них, или (это бывает чаще) потому, что, хотя я и провожу необходимые расчеты, однако делаю это в спешке, неряшливо, рискуя ошибиться. Вот я говорю себе: "По-видимому, электрическое напряжение здесь должно быть таким же, как там: во всяком случае, будем исходить из этого предположения". Само собой разумеется, что в таких случаях я часто ошибаюсь, и получающийся результат оказывается для меня неожиданностью, так как к тому времени, когда эксперимент заканчивается, сделанное допущение уже забыто мною. Эти предположения и натяжки я оставляю открытыми до лекции на тему о моих порочных методах работы. Однако я нисколько не сомневаюсь в том, что действительно испытываю удивление перед машинами.
Я не жду, что этот ответ заставит замолчать моего противника. Вероятно, он скажет, что это удивление происходит вследствие некоторого творческого умственного акта с моей стороны и отражает мое недоверие к машине. Но такая аргументация уводит от вопроса о том, может ли машина чем-либо удивить человека, и возвращает снова к возражению с точки зрения сознания. Этот способ аргументации должен, таким образом, считаться исчерпанным, хотя, быть может, стоит все же отметить то обстоятельство, что если нечто поражает нас своей неожиданностью, то удивление, которое мы испытываем, независимо от того, что является его источником: человек, книга, машина или еще что-нибудь, — требует "творческого умственного акта".
Мнение о том, что машины не могут чем-либо удивить человека, основывается, как я полагаю, на одном заблуждении, которому в особенности подвержены математики и философы. Я имею в виду предположение о том, что коль скоро какой-то факт стал достоянием разума, тотчас же достоянием разума становятся все следствия из этого факта. Во многих случаях это предположение может быть весьма полезно, но слишком часто забывают, что оно ложно. Естественным следствием из него является взгляд, что якобы нет ничего особенного в умении выводить следствия из имеющихся данных, руководствуясь общими принципами.
7. Возражение, основанное на непрерывности действия нервной системы
Нет сомнения в том, что нервная система не является машиной с дискретными состояниями. Небольшая ошибка в информации относительно силы нервного импульса, действующего на нейрон, может привести к значительному изменению импульса на выходе. Исходя из этого, можно было бы как будто предполагать, что нельзя имитировать поведение нервной системы с помощью машины с дискретными состояниями.
То, что машина с дискретными состояниями должна отличаться от машины непрерывного действия, это, конечно, справедливо. Однако если мы будем придерживаться условий "игры в имитацию", то задающий вопросы не сможет использовать это различие. Данную ситуацию можно сделать яснее, рассмотрев другую, более простую, машину непрерывного действия. Для этого особенно хорошо подходит дифференциальный анализатор. (Дифференциальный анализатор — это машина определенного рода, не относящаяся к типу машин с дискретными состояниями, применяемая для вычислений некоторых видов*.) Некоторые из дифференциальных анализаторов выдают ответы в напечатанном виде и поэтому пригодны для игры в имитацию. Цифровая вычислительная машина не может предсказать, какие в точности ответы даст дифференциальный анализатор, решая некоторую задачу, но зато она может сама находить ответы правильного характера на ту же задачу. Например, если требуется найти значение числа ПИ (в действительности приблизительно равное 3,1416), то цифровая вычислительная машина могла бы осуществлять случайный выбор его значения из множества чисел — 3,12; 3,13; 3,14; 3,15; 3,16 — имеющих соответственно такие (например) вероятности выбора: 0,05; 0,15; 0,55; 0,18; 0,06. При этих условиях задающему вопросы будет очень трудно отличить дифференциальный анализатор от цифровой вычислительной машины.
8. Возражение с точки зрения неформальности повеления человека
Невозможно выработать правила, предписывающие, что именно должен делать человек во всех случаях, при всевозможных обстоятельствах. Например, пусть имеется правило, согласно которому человеку следует остановиться, если включен красный свет светофора, и продолжать движение, если свет зеленый; но как быть, если по ошибке оба световых сигнала появятся одновременно? По-видимому, безопаснее всего остановиться. Однако это решение в дальнейшем может быть источником каких-либо новых затруднений. Рассуждая так, мы приходим к заключению, что любая попытка сформулировать правила действия, предусматривающие любой возможный случай, обречена на провал, даже если ограничиться областью транспортной сигнализации. Со всем этим я согласен.
Основываясь на сказанном, доказывают, что мы не можем быть машинами. Я попытаюсь воспроизвести это доказательство, хотя боюсь, что вряд ли сумею сделать это хорошо. Выглядит оно приблизительно так: "Если бы каждый человек обладал определенной совокупностью правил действия, следуя которым он живет, он был бы не чем иным, как машиной. Однако таких правил не существует. Следовательно, человек не может быть машиной". В этом рассуждении бросается в глаза ошибка, связанная с распределенностью термина. Я не думаю, чтобы когда-нибудь это возражение излагали именно в такой форме, однако я убежден, что рассуждение этого рода все же находит применение. Однако оно основано на смешении терминов "правила действия" [rules of conduct] и "законы поведения" [laws of bebaviour], что затемняет вопрос. Под "правилами действия" я понимаю такие предписания, как "Остановитесь, если увидите красный свет"; такие предписания могут определять наши действия и осознаваться нами. Под "законами поведения" я понимаю управляющие человеком естественные законы, например: "Если человека ущипнуть, он вскрикнет". Если в приведенном выше рассуждении вместо "правил действия, которыми человек руководствуется в своей жизни" подставить "законы поведения, управляющие жизнью человека", то ошибка, связанная с нераспределен -ностью термина, оказывается вполне устранимой*.
Имеется в виду очень распространенная логическая ошибка. Ошибочное рассуждение, которое рассматривается в тексте, таково: "Если бы все действия человека определялись некоторой совокупностью правил, то он был бы машиной. Но у человека нет такой совокупности правил. Значит, человек не есть машина".
Данное рассуждение логически неправильно. Чтобы уяснить это, не вдаваясь в подробности логического анализа и классической теории силлогизмов, достаточно сравнить приведенное рассуждение, например, со следующими очевидно ошибочными умозаключениями, которые проведены по совершенно аналогичной схеме:
"Если Вася женится на Кате, то у него будут дети. Но Вася не женится на Кате. Значит, у Васи не будет детей".
"Если молодой человек прочитает книгу "Я + Я", то он сможет помочь себе сам. Но он не прочитает книгу "Я + Я". Значит, он не сможет помочь себе сам". — Прим. И.Д.
Ибо мы убеждены не только в том, что быть управляемым законами поведения — значит быть некоторым родом машины (не обязательно машиной с дискретными состояниями), но что и, наоборот, быть такой машиной означает быть управляемым законами поведения. Однако в отсутствии законов поведения, которые в своей совокупности полностью определяли бы нашу жизнь, нельзя убедиться столь же легко, как в отсутствии законченного списка правил действия. Единственно известный нам способ отыскания таких законов есть научное наблюдение, и, конечно, мы никогда и ни при каких обстоятельствах не можем сказать: "Мы уже достаточно исследовали. Законов, которые полностью бы определяли нашу жизнь и поведение, не существует".
Мы можем с большей убедительностью показать, что любое утверждение такого рода является неоправданным. Действительно, допустим, что мы были бы в состоянии отыскать такие законы (если они существуют). Тогда, если нам будет дана некоторая машина с дискретными состояниями, становится возможным получить посредством наблюдения над ней достаточно данных, чтобы предсказать ее поведение в будущем, причем сделать это можно будет в приемлемый срок, скажем, в 1000 лет. Но, по-видимому, дело обстоит не так. Я вводил в манчестерскую вычислительную машину небольшую программу, занимающую 1000 ячеек памяти, используя которую машина в ответ на введенное в нее 16-значное число выдает в течение двух секунд другое 16-значное число. Попытайтесь-ка извлечь из этого такую информацию о программе машины, которая была бы достаточна для предсказания ее ответа на любое еще не испробованное число. Держу пари, что вам это не удастся.
9. Возражение с точки зрения сверхчувственного восприятия
Я предполагаю, что читателю знакомо понятие о сверхчувственном восприятии и его четырех разновидностях, а именно: о телепатии, ясновидении, способности к прорицанию и психокинезе. Эти поразительные явления, по-видимому, опровергают все наши обычные научные представления. Как бы нам хотелось доказать их несостоятельность! К несчастью, статистические данные, по крайней мере в случае телепатии, на их стороне. Очень трудно перестроить наши представления так, чтобы охватить и эти новые факты, ибо тот, кто верит в сверхчувственное восприятие, по-видимому, не так уже далек от веры в чертей и духов. Ведь взгляд, что жизнь и деятельность человека подчиняются только естественным законам [laws of physics] — как тем, которые уже известны нам, так и тем, которые еще не открыты, но которые предполагаются в некотором смысле аналогичными уже открытым, — напрашивается прежде всего.
Возражение с точки зрения сверхчувственного восприятия, по моему мнению, является достаточно серьезным. На него можно было бы возразить, сказав, что многие научные теории, несмотря на весь шум вокруг сверхчувственного восприятия, остаются применимыми на практике, так что в действительности можно прекрасно обойтись и без него, попросту забыв о его существовании. Это, пожалуй, слабое утешение; есть опасение, что мышление относится как раз к одному из тех явлений, к которым сверхчувственное восприятие имеет, быть может, непосредственное отношение.
Не в столь общей форме возражение, основанное на сверхчувственном восприятии, может быть выражено так: "Будем играть в имитацию, используя в качестве отвечающих на вопросы человека, способного воспринимать телепатические воздействия, и цифровую вычислительную машину.
Задающий вопросы может сформулировать, например, такой вопрос: "Какой масти карта в моей правой руке?". Человек с помощью телепатии или ясновидения дает правильные ответы в 130 случаях из 400. Ответы же машины могут только случайно оказаться правильными, и она сможет угадать масть, скажем, лишь в 104 случаях. Это позволит задающему вопросы отличить человека от машины".
Здесь открывается интересная возможность. Допустим, что в нашей цифровой вычислительной машине имеется устройство случайной выдачи чисел. Тогда весьма естественно использовать его для получения ответов на вопросы. Но тогда это устройство случайной выдачи чисел будет находиться под влиянием психокинетических способностей задающего вопросы. Возможно, что психокинез приведет к тому, что машина будет давать правильные ответы гораздо чаще, чем этого следует ожидать, исходя из вероятностных расчетов, так что задающий вопросы может оказаться не в состоянии сделать правильное заключение относительно того, кто из участников человек, а кто машина. С другой стороны, он может, вообще не задавая никаких вопросов, узнать это с помощью ясновидения: если в дело вмешивается сверхчувственное восприятие, возможно еще и не такое.
Если считать, что телепатия возможна, необходимо ввести ограничения в наш критерий. Можно, например, требовать, чтобы ситуация была аналогична той, которая возникает, когда задающий вопросы обращается к самому себе, а один из участников игры подслушивает его через стенку. Чтобы удовлетворить всем требованиям нашей игры, отвечающих на вопросы следовало бы поместить в комнату, "защищенную от телепатии".
VII. Обучающиеся машины
Читатель, вероятно, уже почувствовал, что у меня нет особенно убедительных аргументов позитивного характера в пользу своей собственной точки зрения. Если бы у меня были такие аргументы, я не стал бы так мучиться, разбирая ошибки, содержащиеся в мнениях, противоположных моему собственному. Сейчас я изложу те доводы, которыми я располагаю.
Вернемся на секунду к возражению графини Лавлейс, согласно которому машина может выполнять лишь то, что мы ей приказываем. Можно сказать, что человек "вставляет" в машину ту или иную идею, и машина, прореагировав на нее некоторым образом, возвращается затем к состоянию покоя, подобно фортепианной струне, по которой ударил молоточек. Другое сравнение: атомный реактор, размеры которого не превышают критических. Идея, вводимая человеком в машину, соответствует здесь нейтрону, влетающему в реактор извне. Каждый такой нейтрон вызывает некоторое возмущение, которое в конце концов замирает. Но если величина реактора превосходит критические размеры, то весьма вероятно, что возмущение, вызванное влетевшим нейтроном, будет нарастать и приведет в конце концов к разрушению реактора. Имеют ли место аналогичные явления в случае человеческого разума и существует ли нечто подобное в случае машин? В первом случае, кажется, следует дать утвердительный ответ. Большинство умов, по-видимому, являются "под критическими", т.е. соответствуют, если пользоваться приведенным выше сравнением, подкритическим размерам атомного реактора. Идея, ставшая достоянием такого ума, в среднем порождает менее одной идеи в ответ. Несравненно меньшую часть умов составляют умы надкритические. Идея, ставшая достоянием такого ума, может породить целую "теорию", состоящую из вторичных, третичных и еще более отдаленных идей. ум [mind] животных, по-видимому, явным образом подкритичен. Развивая нашу аналогию, мы ставим вопрос: "Можно ли сделать машину надкритической?".
Для уяснения поставленного вопроса имеет смысл прибегнуть еще к одной аналогии, именно — уподобить человеческий разум луковице. Рассматривая функции ума или мозга, мы обнаруживаем определенные операции, которые возможно полностью объяснить в терминах чисто механического процесса. Можно сказать, что они не соответствуют подлинному разуму: это своего рода "кожица", которую следует удалить, для того чтобы обнаружить настоящий разум. Однако, рассматривая оставшуюся часть, мы снова найдем "кожицу", которую следует удалить, и т.д. Возникает вопрос: если мы будем продолжать этот процесс, удастся ли нам прийти когда-нибудь к "настоящему" разуму или же в конце концов мы снимем кожицу, под которой ничего не останется ? В последнем случае мы считаем, что разум имеет механический характер. (Правда, он не может быть машиной с дискретными состояниями. Этот вопрос мы уже рассматривали.)
Два последних абзаца вовсе не претендуют на роль убедительных доказательств. Их скорее следовало бы считать аргументами риторического характера.
Единственно убедительное доказательство, которое могло бы подтвердить правильность нашей точки зрения, приведено в начале раздела и состоит в том, чтобы подождать до конца нашего столетия и провести описанный эксперимент. А что же можно сказать в настоящее время? И что можно было бы предпринять уже сейчас, если исходить из предположения, что эксперимент окажется успешным? Как я уже объяснял, проблема заключается главным образом в программировании. Прогресс в инженерном деле также необходим, однако маловероятно, чтобы затруднение возникло с этой стороны. Оценки емкости памяти человеческого мозга колеблются от 1010 до 1015 двоичных единиц. Я склоняюсь к нижней границе и убежден, что лишь очень небольшая доля емкости памяти человека используется в высших типах мышления, причем из того, что используется, большая часть служит сохранению зрительных восприятии. Для меня было бы неожиданностью, если бы оказалось, что для игры в имитацию на удовлетворительном уровне требуется емкость памяти, превышающая 109, во всяком случае если бы игра велась против слепого человека. (Заметьте: емкость "Британской энциклопедии", 11-е изд., составляет 2 х 109.) Емкость памяти, равная 107, практически представляется вполне осуществимой даже при современном состоянии техники. Вероятно, нет необходимости вообще далее увеличивать скорость машинных операций*. Те части современных машин, которые можно рассматривать как аналоги нервных клеток, работают примерно в тысячу раз быстрее последних.
Это создает "запас надежности"', могущий компенсировать потери в быстроте, возникающие во многих случаях. Перед нами стоит задача составить машинную программу для игры в имитацию. В настоящее время скорость моей работы программиста составляет примерно тысячу знаков в день; если исходить из такой скорости программирования, то получится, что шестьдесят работников могли бы полностью закончить работу, о которой идет речь, если бы они работали непрерывно в течение пятидесяти лет, при условии, конечно, что ничего не пойдет в корзину для бумаг. Желателен, по-видимому, какой-нибудь более производительный метод.
Пытаясь имитировать ум [mind] взрослого человека, мы вынуждены много размышлять о том процессе, в результате которого человеческий интеллект достиг своего нынешнего состояния. Мы можем выделить три компонента:
1) первоначальное состояние ума, скажем, в момент рождения;
2) воспитание, объектом которого он был;
3) другого рода опыт, воздействовавший на ум, — опыт, который нельзя назвать воспитанием.
Почему бы нам, вместо того чтобы пытаться создать программу, имитирующую ум взрослого, не попытаться создать программу, которая бы имитировала ум ребенка? Ведь если ум ребенка получает соответствующее воспитание, он становится умом взрослого человека. Как можно предположить, мозг ребенка в некотором отношении подобен блокноту, который мы покупаем в киоске: совсем небольшой механизм и очень много чистой бумаги. Наш расчет состоит в том, что механизм в мозгу ребенка настолько несложен, что устройство, ему подобное, может быть легко Запрограммировано. В качестве первого приближения можно предположить, что количество труда, необходимое для воспитания такой машины, почти совпадает с тем, которое необходимо для воспитания ребенка.
Таким образом, мы расчленили нашу проблему на две части: на задачу построить "программу-ребенка" и задачу осуществить процесс воспитания. Обе эти части тесно связаны друг с другом. Вряд ли нам удастся получить хорошую "машину-ребенка" с первой же попытки. Надо провести эксперимент по обучению какой-либо из машин такого рода и выяснить, как она поддается научению. Затем провести тот же эксперимент с другой машиной и установить, какая из двух машин лучше. Существует очевидная связь между этим процессом и эволюцией в живой природе, которая обнаруживается, когда мы отождествляем:
• структуру "машины-ребенка" с наследственным материалом;
• изменения, происходящие в "машине-ребенке", с мутациями;
• решение экспериментатора с естественным отбором. Тем не менее можно надеяться, что этот процесс будет протекать быстрее, чем эволюция. Выживание наиболее приспособленных является слишком медленным способом оценки преимуществ. Экспериментатор, применяя силу интеллекта, может ускорить процесс оценки. В равной степени важно и то, что он не ограничен использованием только случайных мутаций. Если экспериментатор может проследить причину некоторого недостатка, он, вероятно, в состоянии придумать и такого рода мутацию, которая приведет к необходимому улучшению.
Невозможно применять в точности один и тот же процесс обучения как к машине, так и к нормально развитому ребенку. Например, машину нельзя снабдить ногами, поэтому ее нельзя попросить выйти и принести ведро угля. Машина, по-видимому, не будет обладать глазами. И, как бы хорошо ни удалось восполнить эти недостатки с помощью различных остроумных приспособлений, такое существо нельзя будет послать в школу без того, чтобы другие дети не потешались над ним. И вот такое существо мы должны чему-то научить. Отметим, что не стоит особенно беспокоиться относительно ног, глаз и т.д. Пример мисс Елены Келлер* показывает, что воспитание возможно, если только удается тем или иным способом установить двухстороннюю связь между учителем и учеником.
Случай Е. Келлер — не единственный случай воспитания слепоглухонемых. В Академии педагогических наук РСФСР в качестве научного сотрудника работала О. И. Скороходова, которая в 5 лет потеряла зрение и слух. Она была воспитана в Харьковской клинике для слепоглухонемых детей. Известна книга О. И. Скороходовой "Как я воспринимаю и представляю окружающий мир". М., 1954. — Прим. И.Д.
Обычно процесс обучения в нашем представлении связан с наказаниями и поощрениями. Идея применения какой-либо формы этого принципа обучения может лежать в основе конструирования и программирования некоторых простых "машин-детей". В этом случае машину следует устроить таким образом, чтобы поступление в нее сигнала-"наказания" приводило к резкому уменьшению вероятности повторения тех реакций машины, которые непосредственно предшествовали этому сигналу, в то время как сигнал-"поощрение", наоборот, увеличивал бы вероятность тех реакций, которые ему предшествовали (которые его "вызвали" ). Все это не предполагает со стороны машины никаких чувств. Я проделал несколько экспериментов с одной такой "машиной-ребенком" и достиг кое-какого успеха в обучении ее некоторым вещам, но метод обучения был слишком необычен, чтобы эксперимент можно было считать действительно успешным.
Применение поощрений и наказаний в лучшем случае может быть лишь частью процесса обучения. Проще говоря, если у учителя нет других средств общения со своими учениками, то количество информации, которое может получить ученик, не превышает общего числа примененных к нему поощрений и наказаний. Вероятно, к тому времени, когда ребенок выучит наизусть стихотворение "Касабьянка"*, он будет до крайности измучен, если процесс обучения будет идти по методу игры в "20 вопросов"*, причем каждое "нет" учителя будет принимать для ученика форму подзатыльника. В силу этого необходимо иметь какие-то другие, "неэмоциональные" каналы связи. Если такие каналы имеются, то, применяя поощрения и наказания, машину можно было бы научить выполнять команды, отдаваемые на каком-либо — например, символическом — языке. Эти команды следует передавать по "неэмоциональным каналам". Применение такого символического языка значительно снизит число требуемых поощрений и наказаний.
О том, какая степень сложности является наиболее пригодной для "машины-ребенка", могут быть различные мнения. Можно стремиться к тому, чтобы "машина-ребенок" была настолько простой, насколько этого возможно добиться, не нарушая общих принципов. Можно идти противоположным путем: "встраивать" сложную систему логического вывода*. В последнем случае значительную часть запоминающего устройства заняли бы определения и суждения [propositions]. Суждения по своему характеру должны быть различного рода, например: утверждения о хорошо известных фактах, предположения, математически доказанные теоремы, высказывания авторитетных лиц, выражения, по своей логической форме являющиеся суждениями, но не претендующие на верность. Некоторые из этих суждений могут быть охарактеризованы как "приказания". Машину следует устроить так, чтобы, как только некоторое приказание будет оценено ею как "вполне достоверное" [well-established}, автоматически выполнялась соответствующая операция. Чтобы пояснить это, предположим, что учитель говорит машине: "Теперь выполняй домашнее задание", — а машина реагирует на это тем, что ситуация "Учитель говорит машине: "Теперь выполняй домашнее задание" включается в число вполне достоверных фактов. Другим фактом такого же рода в ней может быть: "Все, что говорит учитель, истинно". Комбинация этих фактов может в заключение вести к тому, что приказание "Теперь выполняй домашнее задание" также будет включено в разряд вполне надежных фактов, а это, в свою очередь, будет значить в силу устройства нашей машины, что последняя действительно начнет выполнять домашнее задание, — что нам и было нужно. Процесс логического вывода, применяемый машиной, вовсе не обязательно должен быть таков, чтобы он удовлетворял требованиям самых строгих логиков. Например, может отсутствовать иерархия типов*. Но это отнюдь не означает, что вероятность связанной с этим ошибки, которую может сделать машина, больше вероятности того, что человек может упасть в пропасть, если ее край не будет огорожен. В рассматриваемом случае подходящие приказания (выраженные внутри системы формального вывода, а не составляющие часть ее правил), например, такие, как "Не используйте некоторый класс, если он не является подклассом класса, который ранее упоминался учителем", могут иметь эффект, аналогичный тому, какой имеет предупреждение: "Не подходите слишком близко к краю обрыва".
Приказания, которые может выполнять машина, не имеющая ни рук, ни ног, должны касаться преимущественно интеллектуальных сторон деятельности, как это было в приведенном выше примере (с домашним заданием). Из такого рода приказов наиболее важными будут приказания, определяющие порядок, в котором следует применять правила рассматриваемой логической системы. Ибо на каждой стадии применения логической системы перед нами открывается большое число возможных шагов, которые исключают друг друга и любой из которых мы можем осуществить, следуя правилам рассматриваемой системы. Как производится такой выбор — в этом и выражается различие между глубоким и посредственным умом, но это не имеет отношения к правильности или неправильности рассуждении. Суждения, которые порождают приказания такого рода, могут быть, например, такими: "Если упоминается Сократ, применяй силлогизм модуса Barbara"— или: "Если один метод приводит к результату быстрее, чем второй, не применяй более медленного". Одни из них могут исходить от "авторитетного лица", другие же могут вырабатываться самой машиной, например, с помощью неполной индукции.
Модус силлогизма — схема (правило) логического умозаключения. Понятие модуса силлогизма относится к схоластической (восходящей к Аристотелю) логике; каждый из модусов имеет специальное название. Классический пример умозаключения по модусу Barbara следующий: "Все люди смертны. Сократ — человек. Следовательно, Сократ смертей". — Прим. И.Д.
Некоторым читателям мысль об обучающейся машине может показаться парадоксальной. Как могут меняться правила, по которым машина производит операции? Ведь правила должны полностью описывать поведение машины независимо от того, какова была ее предыстория и какие изменения она претерпела. Таким образом, правила должны быть абсолютно инвариантными относительно времени. Все это, конечно, верно. Объяснение этого парадокса состоит в том, что правила, которые меняются в процессе научения, не претендуют на это, ибо их применимость носит преходящий характер. Читатель может провести параллель с Конституцией Соединенных Штатов*.
Важная особенность обучающейся машины состоит в том, что ее учитель в значительной мере не осведомлен о многом из того, что происходит внутри нее, хотя он все же в состоянии в известных пределах предсказывать поведение своей ученицы. Сказанное особенно применимо к дальнейшему воспитанию машины, прошедшей уже хорошую подготовку и вышедшей из начальной стадии "машины-ребенка". Такое положение, очевидно, в корне отличается от обычного-подхода, связанного с применением машин для вычислений, когда мы стремимся к тому, чтобы иметь ясное представление о состоянии машины в любой момент вычисления, достичь чего можно лишь с трудом. В свете сказанного взгляд, что "машина может выполнить только то, что мы умеем ей предписать*, кажется странным. Большинство программ, которые мы можем ввести в машину, вызывают в ее работе кое-что такое, что мы вообще не в состоянии осмыслить или рассматриваем как чисто случайное поведение. Интеллектуальное [intelligent] поведение предполагает, по-видимому, некоторое отступление от абсолютно детерминированного [disciplined] поведения в процессе вычисления; это отступление, однако, должно быть очень незначительным, чтобы не вызвать полностью беспорядочного поведения или бессмысленных повторений отдельных циклов. Другой важный результат обучения как способа подготовки нашей машины для участия в игре в имитацию, состоит в том, что "присущая человеку склонность к ошибкам" будет, по-видимому, обойдена естественным образом, т.е. без специального "натаскивания". Процесс обучения не обязательно должен быть успешным во всех случаях; если бы это было так, то не встречались бы случаи неудачи в обучении.
Вероятно, в обучающуюся машину имеет смысл ввести случайный элемент. Случайный элемент довольно полезен, когда мы ищем решение какой-нибудь задачи. Пусть, например, требуется найти число, расположенное между 50 и 200 и равное квадрату суммы своих цифр; мы можем сначала проверить число 51, затем 52 и продолжать до тех пор, пока не найдем то, которое удовлетворяет условию задачи. Но мы можем поступить и иначе: выбирать числа наугад до тех пор, пока не получим то, которое нам нужно. Этот метод имеет то преимущество, что он не требует хранения в памяти уже проверенных значений; однако он имеет и отрицательную сторону, состоящую в том, что одно и то же число может быть подвергнуто проверке повторно, но это не так уж существенно, если задача имеет несколько решений. Систематический метод имеет другой недостаток: может случиться, что придется проверять массу значений, не содержащих ни одного решения, прежде чем будет найдено первое число, обладающее нужным свойством.
В нашем случае процесс обучения можно рассматривать как поиски такой формы поведения, которая бы удовлетворяла требованиям учителя (или какому-нибудь другому критерию). Поскольку в этом случае, по-видимому, имеется весьма большое число решений, отвечающих предъявленным требованиям, постольку метод случайного выбора представляется нам предпочтительнее систематического. Следует отметить, что метод случайного выбора применяется и в другом аналогичном процессе — в эволюции. Но там систематический метод невозможен вообще. Неясно, каким образом было бы возможней в процессе эволюции сохранять информацию о тех разнообразных генетических комбинациях, которые были испробованы, с тем чтобы предупредить возможность их повторного применения.
Мы можем надеяться, что машины в конце концов будут успешно соперничать с людьми во всех чисто интеллектуальных областях. Но какие из этих областей наиболее пригодны для того, чтобы начать именно с них? Решение даже этого вопроса наталкивается на затруднения. Многие считают, что начать лучше всего с какой-нибудь очень абстрактной деятельности, например, с игры в Шахматы. Другие предлагают снабдить машину хорошими органами чувств, а затем научить ее понимать и говорить по-английски. В этом случае машину можно будет обучать, как ребенка: указывать на предметы и называть их и т.д. В чем состоит правильный ответ на этот вопрос, я не знаю, но думаю, что следует испытать оба подхода.
Мы можем заглядывать вперед лишь на очень небольшое расстояние, но уже сейчас очевидно, что най предстоит еще очень многое сделать в той области, которая была предметом настоящей статьи.
1950г.
* Институт Гэллапа
— Американский институт общественного мнения American Institute of Public Opinion. Основан Дж. Гэллапом (GeorgeGallup) в l935r.* Мост через реку Форт
— известный мост консольно-арочного типа, в два пролета, перекрывающий реку форт (Шотландия) при впадении ее в залив Ферт-оф-Форт. Сооружен в 1882—1889 гг. и в течение 28 лет держал мировой рекорд длины пролетов (длина каждого пролета — свыше 518 м, длина моста — около 1626 м).* Чарлз Бэббидж
(Charles Babbage) (1792—1871) —английский ученый, работавший в области математики, вычислительной техники и механики. Выступил инициатором применения механических устройств для вычисления и печатания математических таблиц. В 1812 г. у Бэббиджа возникла идея разностной вычислительной машины (Difference Engine). Строительство этой машины, которая должна была вычислять любую функцию, заданную ее первыми пятью разностями, началось в 1823 г. на средства английского правительства, однако в 1833 г. работа была прекращена главным образом в связи с финансовыми затруднениями. К этому времени у Бэббиджа возник проект другой, более совершенной машины. Эта машина, которую Бэббидж назвал "Аналитической машиной" (Analitical Engine), должна была проводить вычислительный процесс, заданный любыми математическими формулами. Бэббидж весь отдался конструированию своей новой машины, однако к моменту его смерти она так и не была закончена. Сын Бэббиджа завершил строительство части машины и провел успешные опыты по применению ее для вычислений некоторого рода.* Аюкасовская кафедра
в Тринити-колледже основана в 1663 г. на средства, пожертвованные Генри Люкасом. Первым люкасовским профессором был учитель Ньютона Барроу, вторым — сам Ньютон. Получение этой кафедры, сохранившейся до нашего времени, считалось всегда большой честью.* Манчестерская машина
была построена в Манчестерском университете в конце 40-х годов. Конструирование машины происходило под руководством Вильямса (Р.С. Williams) и Килберна (T.Kilburn). В разработке и отладке машины принимал участие Тьюринг, который с этой целью в 1948 г. был приглашен в Манчестерский университет. Тьюринг занимался математическими вопросами, связанными с Манчестерской машиной, и особенно вопросами программирования.* Единицы
, о которых говорит здесь Тьюринг, получили название "битов" (bits) По причинам, связанным с компьютеростроением, основной единицей измерения емкости машинной памяти стали "байты" (bytes) Ответ на вопрос "Сколько бит [ов] в байте?" с исторической точки зрения довольно темен (байт — емкость памяти, предназначенной для размещения одного символа), но стандартом de facto является соглашение 1 байт = 8 бит. Более крупными производными единицами являются килобайт (Кб) = 210 = 1024 байт, мегабайт (Мб) = 210 = 1024 Кб Сейчас уже никого не удивляют гигабайты (Г6) и даже терабайты (Тб) Для более точного выражения единиц памяти (например, в синтезаторостроении) употребляются также единицы килобит (Кбит), мегабит (Мбит) и т.д.* Возможно,
эта точка зрения еретична. Св. Фома Аквинский (Summa Theologica; его взгляд излагается в книге Bertrand Russell, History of Western Philosophy, Simon and Schuster, New York, 1946, p. 458 [русское издание, например: Б.Рассел. История западной философиии. Новосибирск, изд-воНГУ, 1994] ) утверждает, что Бог не может лишить человека души, но что это не является реальным ограничением его всемогущества, а есть всего лишь результат того факта, что человеческие души бессмертны и, следовательно, неуничтожимы.*K.GodeI.
Uber formal unentscbeidbare Sat^e der Principia Matematica und verwandter Systeme, I. Monat. Math. Ph., B. 38, 1931, S. 173-198.*Alonzo Church.
An Unsolvable Problem of Elementary Number Theory. Amer. J. Math., v. 58, 1936, p. 345—363; S.C. Cleene. General Recursive Functions of Natural Humbers. Math. Ann., B. 112, 1936, S. 727—742; A.M. Turing. On Computable Numbers, with an Application to the Entscheidungsproblem. Proc. Lond. Math. Soc., ser. 2, v. 42, 1936-1937, pp. 230-265.* Здесь
речь идет о так называемых (в современной терминологии) алгоритмически неразрешимых проблемах. Вот пример неразрешимой проблемы, который я изложу здесь в терминах "повседневного" компьютера. Требуется составить программу U, которая бы по любому подаваемому ей на вход файлу X, содержащему текст программы (на каком-нибудь языке программирования, скажем, стандартном ANSI С), определяла бы, остановится ли когда-нибудь программа из файла Х в процессе своей работы, получив на вход известные данные, или "зациклится". Если программа Х зациклится, то программа U должна показать на экране фотографию юноши, иначе — девушки, после чего закончить свою работу. (Такого рода "проверяющая на зацикливаемость" программа U. была бы, очевидно, довольно полезна для проверки создаваемых компьютерных программ.) Оказывается, написать эту "проверяющую программу" U невозможно в принципе (даже если допустить, что компьютер, на котором выполняется U, имеет сколь угодно большую память и может работать неограниченно (астрономически) долгое время). Приведенный пример (так называемая "неразрешимость проблемы остановки") впервые был рассмотрен в цитированной выше работе Тьюринга 1936 г. — в то время, когда еще не было никаких компьютеров и программ для них!* G.Jefferson.
The Mind of Mechanical Man. Lister Oration for 1949, Britisch Med. J., v. 1, 1949, p. 1105-1121.* Листеровские чтения.
Джозеф Аистер (Joseph Lister) (1827—1912) — выдающийся английский хирург.* Солипсизм
(от лат. solus — единственный и ipse — сам) — взгляд, согласно которому единственной достоверной реальностью являются внутренние переживания субъекта, его ощущения и мышления.*Принцип неполной индукции —
принцип логики, согласно которому разрешается делать обобщающее заключение о принадлежности некоторого свойства я всем предметам данного класса. А на основании того, что установлена принадлежность свойства а лишь некоторым (не всем) предметам класса А, именно тем, которые рассмотрены в ходе индукции. Вывод, основанный на принципе неполной индукции — даже при условии достоверности исходных данных,— не достоверен, а только более или менее вероятен.* Графиня Аавлейс, Ада.
Августа (Ada Augusta, the Countess of Lovelace) принадлежала к тем немногим современникам Бэббиджа, которые вполне оценили значение его идей. Она была дочерью английского поэта Байрона (родилась в 1815 г., умерла в 1852 г.). Лавлейс получила хорошее математическое образование, сначала под руководством своей матери, а потом под руководством проф. Августа де Моргана (Augustus de Morgan), одного из создателей математической логики. С Бэббиджем и его машинами она познакомилась еще в юности. В 1840 г. написала о Бэббидже работу и опубликовала ее в Scientific Memoirs (ed. by R.Taylor, 3, 1842, 691-т731), присоединив к ней обширные примечания переводчика, более чем в два раза превосходившие по объему текст Менабреа. Эти примечания относились к принципам работы Аналитической машины и ее применению и были высоко оценены Бэббиджем. См: faster than Thought. A Symposium on Digital Computing Machines Ed. by B.V. Bowden. London, 1953, chap. 1. В приложении к книге воспроизведены работа Менабреа в переводе Лавлейс и работа самой Лавлейс (Notes by the Translator) .* D.R. Hartree,
Calculating Instruments and Machines, New York, 1949.*Дифференциальный анализатор
— вычислительная машина, разработанная В.Бушем (Vannevar Bush) и его сотрудниками в Массачусетсском технологическом институте в Кембридже (США) в конце 20-х годов и предназначенная для решения широкого класса обыкновенных дифференциальных уравнений. Дифференциальный анализатор — машина непрерывного действия; при решении задач мгновенные значения переменных выражаются положениями вращающихся валов машины (с учетом числа сделанных валом полных оборотов и направления вращения). Первая модель машины была чисто механическим устройством. В дальнейшем дифференциальный анализатор был усовершенствован его автором и превратился в электромеханическую машину.* Если в приведенном
выше рассуждении вместо "правил действия" подставить "законы поведения" (в смысле, разъясненном в тексте), то логическая ошибка легко устраняется за счет замены посылки обратным ей суждением: "Все машины отличаются тем, что их поведение полностью определено некоторыми законами" (в истинности которого, говорит Тьюринг, мы убеждены), в котором термин "машины" распределен (так как речь идет обо всех машинах). Но тут оказывается, что, в отличие от случая, когда речь шла о "правилах действия", истинность второй посылки вызывает сомнения; по мнению Тьюринга, мы не имеем возможности убедиться в ее достоверности.* Здесь,
разумеется, имеются в виду требования автора, предъявляемые к машинам, предназначенным для игры в имитацию. Напомню, что емкость памяти в 109 двоичных единиц (бит), о которых говорит автор, соответствует примерно 120 Мб. Если применить его расчеты, скажем, к современным персональным компьютерам, то нужно оговорить, что здесь речь идет о "чистом" (минимальном) объеме памяти, потребном для решения задачи игры в имитацию. — Прим. И.Д.* Елена Келлер (Helen Keller) (1880-1968)
- американская слепоглухонемая, получившая высшее образование. В возрасте полутора лет в результате болезни потеряла зрение и слух и стада немой. Когда девочке было 6 лет, родители пригласили воспитательницу, которая посредством осязания научила ребенка говорить, а затем читать и писать (по системе для слепых). Е.Келлер прошла школьный курс, изучила языки, окончила университет; она является автором ряда книг.* "Касабьянка" (Casabianca)
— стихотворение английской поэтессы Фелиции Хеманс (Felicia Hemans, 1793—1835). Повествует о мальчике десяти лет, сыне капитана Касабьянки, который вместе с отцом погиб на горящем военном корабле, отказавшись покинуть судно, взорванное командиром Касабьянкой во время морского боя.* "двадцать вопросов" —
распространенная в Англии игра в вопросы и ответы. Обычно ведется так. Один из играющих задумывает некоторое понятие. Другой играющий отгадывает задуманное, задавая вопросы, предполагающие ответы (обязательно правдивые) вида "да" или "нет". Количество вопросов, которое имеет право задать отгадчик, не должно превышать некоторого заранее установленного числа. Отгадчик выигрывает, если при указанных условиях отгадает, что же было задумано первым играющим.* Лучше сказать
"впрограммировать", так как наша "машина-ребенок" будет программироваться на цифровой вычислительной машине. Однако указанная логическая система не будет обучаемой.* Здесь имеется в виду
иерархия типов, предложенная Бертраном Расселом с целью избежать противоречии (антиномий), обнаруженных в логике и теории множеств в конце XIX — начале XX столетия.* К Конституции США
(выработана и утверждена в 1787— 1789 гг.) при сохранении ее основного содержания (изменения и дополнения к американской Конституции обставлены весьма сложной процедурой) за время, истекшее после ее принятия, был сделан целый ряд поправок (более двадцати).* Сравните
эту формулировку с высказыванием госпожи Лавлейс, в котором нет слова "только".