Уважаемые коллеги! В последнее время интерес к решению задач с использованием электронных таблиц стремительно растет не только у преподавателей информатики, но и у учителей других дисциплин, в частности, биологии. Тем не менее основная нагрузка в изучении электронных таблиц приходится на уроки информатики. Учитель биологии может помочь в подборе и составлении задач, которые дадут возможность, во-первых, отработать учебный материал по электронным таблицам, во-вторых, закрепить знания по биологии и, в-третьих, наглядно продемонстрировать учащимся существование межпредметных связей и, таким образом, повысить мотивацию к изучению сразу двух дисциплин.

Задание, рассматриваемое в статье, относится к курсу экологии. Основная цель задания — моделирование отношений «хищник — жертва» в природном сообществе. Поскольку моделирование естественного процесса неизбежно приводит к упрощению и схематизации природных явлений, учитель биологии может рассматривать это задание на своих уроках как в 8-м, так и в 9-м, в 10-м или в 11-м классе. Наибольшая трудность здесь заключается в составлении электронных таблиц, поэтому время для выполнения этой части работы выбирает учитель информатики.

Идея задания позаимствована из американского учебника по биологии для школьников 16—17 лет. W.D. Scbraer, H.J. Stolty, Biology. “The Study of life”, Nelson, 1992, ISBN 0-13-080681-1.

Задание состоит из пяти задач с нарастающим уровнем сложности. Каждая задача содержит общее условие, а также дополнительное (индивидуальное) условие и индивидуальный вопрос. Если в задаче нет специальных указаний относительно общего условия, его нужно принимать в расчет при решении задачи.

Общее условие

Цель задания — составить упрощенную математическую модель взаимоотношений хищника и жертвы в сообществе. Начальная численность популяции оленя (жертвы) составляет 2000 особей. Оленями питаются два хищника — волк и пума. Выжившая к концу каждого года часть популяции оленей увеличивает свою численность на 40%. Начальная численность популяции волков составляет 15 особей, один волк потребляет по 30 оленей ежегодно, годовой прирост популяции волков составляет 10%. Начальная численность пум неизвестна, одна пума потребляет по 20 оленей ежегодно, годовой прирост популяции пум составляет 20%. Смертность оленей по иным причинам равна нулю. Смертность волков и пум равна нулю.

 Задача 1

Рассчитайте, какова будет численность оленей через 1, 3, 5 и 10 лет при полном отсутствии хищников. Отобразите изменения численности оленей в течение данного периода времени графически.

 Задача 2

Рассчитайте, какова будет численность оленей через 1, 3, 5 и 10 лет, если начальная численность волков составляет 15 особей и не изменяется на протяжении указанного периода времени.

Отобразите изменения численности оленей в течение данного периода времени графически. Сравните полученный результат с результатом задачи 1.

 Задача 3

Рассчитайте, какова будет численность оленей через 1, 3, 5 и 10 лет, если начальная численность волков составляет 15 особей и возрастает на 10% ежегодно.

Отобразите изменения численности оленей в течение данного периода времени графически. Сравните полученный результат с результатами задачи 1 и задачи 2.

 Задача 4

Рассчитайте, какой должна быть начальная численность растущей популяции волков, чтобы численность оленей была относительно стабильна (т.е. равнялась примерно 2000) в течение первых пяти лет существования популяции.

Как будет изменяться численность популяции оленей в течение последующих пяти лет? Представьте все полученные данные графически.

 Задача 5

Рассчитайте, какой должна быть начальная численность волков и пум, чтобы численность оленей была относительно стабильной (т.е. равнялась примерно 2000) в течение первых пяти лет существования популяции.

Как будет изменяться численность популяции оленей в течение последующих пяти лет? Представьте все полученные данные графически.

Решение

Каждую задачу в нашем задании можно решать по отдельности. В этом случае учитель может использовать менее сложные задачи (задачи 1 —3) либо в процессе объяснения нового материала для всего класса либо в качестве закрепления или контроля для "слабых" учеников. Однако гораздо интереснее рассматривать задание как систему из пяти задач — тогда его можно преподнести как небольшой проект и выполнить совместно с учителем биологии (экологии) Выполнение и обсуждение результатов такого проекта занимает 3—4 урока. Не секрет, что учебного времени постоянно не хватает, поэтому лучше дать это задание на дом как самостоятельную работу, предоставив от нескольких дней до недели. В этом случае нужно обязательно выделить хотя бы один урок на обсуждение результатов работы. Очевидно, что для выполнения задания, поданного таким образом, учащиеся уже должны быть ознакомлены со всеми необходимыми приемами работы с электронными таблицами. Презентация проекта может быть проведена совместно с учителем биологии. В этом случае в обсуждение включаются вопросы о биологии и экологии животных, упоминаемых в задачах, чтобы подвести рассматриваемую модель как можно ближе к реальному сообществу.

Имея перед глазами условия всех пяти задач, нам будет легче представить, как выглядит окончательный вариант решения. Размер электронной таблицы должен быть такой, чтобы на одной координатной плоскости можно было начертить диаграммы в любой комбинации.

 Составление электронной таблицы в Microsoft Excel

В первую строку таблицы будем вносить константы, входящие в условие задания: в ячейку А1 внесем начальную численность оленей, в ячейку В1 — ежегодное увеличение популяции оленей, в ячейку С1 — начальную численность волков, в ячейку D1 — количество оленей, поедаемых одним волком в год, в ячейку El — годовой прирост численности волков, ячейку F1 оставим для подбора начальной численности пум в задаче 5, в ячейку G1 внесем количество оленей, поедаемых одной пумой в год, в ячейку HI — годовой прирост популяции пумы (см. рис. 1).

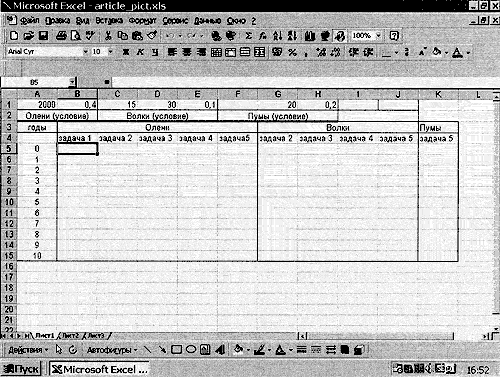
Рис.1. Первоначальный вид электронной таблицы

Решение будем записывать в ячейки, расположен­ные ниже. В экологии "начальным" годом принято считать "нулевой" год, поэтому годы интересующего нас периода мы пронумеруем от 0 до 10. Тогда ответ на вопрос о численности оленей, скажем, через 5 лет окажется в ячейке, расположенной напротив года под номером 5 (см. рис. 1).

Численность оленей упоминается в задании пять раз (в задачах 1—5), численность волков упоминается че­тыре раза (в задачах 2—5), численность пумы — 1 раз (в задаче 5). Исходя из этого,  в начале выполне­ния задания таблица будет выглядеть так, как показа­но на рис. 1.

 Формулы и комментарии к решению

 Задача 1

1. Численность оленей будем вычислять в ячейках В5:В15. Присваиваем ячейке В5 значение $А$1, где $А$1 — абсолютный адрес ячейки А1, в которую мы занесли начальную численность популяции оленей. Поскольку по условию начальная численность оленей одинакова во всех пяти задачах, можно скопировать содержимое ячейки В5 в ячейки С5 : F5.

2. Записываем в ячейку В6 формулу для вычисления численности оленей в каждом следующем году:

=В5+В5*$В$1, где $В$1 — абсолютный адрес ячейки В1, в которую мы занесли число, характеризующее рост популяции оленей.

3. Выделяем ячейку В 6 и копируем формулу в ячейки В 7 : В15 включительно.

 Задача 2

1. Численность оленей будем вычислять в ячейках С5 : С15. Ячейке С5 мы уже присвоили значение $А$1.

2. Формулу =(C5-G5*$D$1) * (1+$В$1) заносим в С6, здесь $D$1 — абсолютный адрес ячейки D1, в которую мы занесли число оленей, поедаемых одним волком в год. Копируем содержимое ячейки С6 в ячейки С7.-С15.

3. Численность волков, которая в данной задаче постоянна, будет храниться в ячейках G5:G15. BG5 за­писываем = $С$1, где $С$1 — абсолютный адрес ячейки С1, в которую мы занесли начальную численность волков. Копируем содержимое ячейки G5 в ячейки G6: G15 включительно.

 Задача 3

 1. Численность оленей будем вычислять в ячейках D5 : D15. Численность волков — в ячейках Н5 : Н15.

2. ВН5 заносим =$С$1.

3. В Н6 заносим =Н5+Н5*$Е$1, где $Е$1 — абсолютный адрес ячейки Е 1, в которую мы записали значение годового прироста популяции волка. Копируем формулу в ячейки Н7 : HI 5.

4. BD6 заносим =(D5-H5*$D$1) * (1+$В$1). Копируем формулу в ячейки D7 : D15.

Задача 4

 

1. Численность оленей будем вычислять в ячейках Е5 : Е 15, численность волков — в ячейках I5:I15.

2. В задаче требуется подобрать такое начальное число волков, при котором численность оленей будет изменяться минимально в течение первых пяти лет суще­ствования популяции. Подбирать такое число будем в ячейке I1, поэтому в I5 заносим формулу =$I$1.

3. В I6 помещаем = I5+I5*$E$1. Копируем формулу в ячейки I7:I15.

4. В Е6 помещаем =(E5-I5*$D$1) * (1+$В$1) . Копируем формулу в ячейки Е7 : Е15.

5. Подбираем число в ячейке I1 так, чтобы в ячейках Е5 : Е9 получилось число, примерно равное 2000. В результате получаем равные значения в ячейках I1 и I7.

Задача 5

1. Численность оленей будем вычислять в ячейках F5:F15, численность волков — в ячейках J5:J15, численность пум — в ячейках К5 : К15.

2. В ячейки J6 и Кб надо записать формулы для определения численности волков и пум, исходя из годового прироста популяций и их начальной численности. Вопрос в задаче 5 аналогичен вопросу в задаче 4 и заключается в выяснении начальной численности хищников, удовлетворяющей условию. Численность пум мы будем подбирать в ячейке F1. Что касается численности волков, то мы не можем снова использовать ячейку I1, так как изменения в ней повлекут за собой изменения в колонке Е5 : Е15, где представлены результаты предыдущей задачи. По этой причине используем дополнительную ячейку J1, с ней и будем проводить требуемый вычислительный эксперимент.

3. В J5 заносим формулу =$J$1; в J6 заносим ==J5+J5 * $Е$ 1. Копируем последнюю формулу в ячейки J6:J15.

4. В К 5 заносим =$F$1; в Кб заносим =К5+К5*$Н$1, где $Н$1 — абсолютный адрес ячейки H1, в которую мы записали значение годового прироста популяции пумы. Копируем последнюю формулу в ячейки Кб : К15.

5. В F6 заносим

=(F5-J5*$D$1-K5*$G$1)*(1+$В$1),

где $G$1 — абсолютный адрес ячейки G1, куда мы занесли число оленей, поедаемых одной пумой в год. Копируем формулы в ячейки F6 : F15.

6. Получаем ответ: в ячейке F1 10; в ячейке J1 10. При выполнении задания необходимо помнить об ограничениях, накладываемых биологическим смыслом задач:

• все получаемые в результате расчетов значения должны быть целыми неотрицательными числами, так как все они указывают на абсолютное количество животных и, следовательно, не могут быть ни отрицательными, ни дробными;
• с точки зрения экологии нужно не округлять зна­чения, а брать целую часть числа путем отбрасывания дробной части, поскольку в реальной популяции можно учитывать только "целых" животных (так, число 3860,8 превращается в число 3860). Важно подчеркнуть, что это не округление и поэтому не идет вразрез со знаниями учащихся о правилах округления чисел;
• при подборе начальной численности хищников в задаче 5 (ячейки F1 и J1) надо следить, чтобы выполнялись все условия задачи. Так, если ученик решил брать в качестве значения целую часть числа, начальное количество пум (F1) должно быть больше или равно 5, так как при значениях меньше 5 численность популяции пумы не может расти. Например, если число животных равно 4, то при приросте в 20 % на следующий год получим:
• 44-4' 0,2 = 4,8. Взяв целую часть числа 4,8, получим 4 пумы, как и в предыдущий год, а это противоречит условию задачи. Начальное количество волков (J1) по той же причине не может быть меньше 10;
• ни F1, ни J1 не могут быть меньше 2.

При постановке задачи можно намеренно не вдаваться в описанные подробности, а лишь напомнить учащимся о том, что задача должна иметь биологический смысл. В этом случае учитель получает возможность оценить уровень развития биологического мышления школьников и их умение аргументировать ответ.

Конечный вариант таблицы представлен на рис. 2.

Рис. 2. Результаты решения задач 1-5

Графическое представление данных

Для графического представления динамики численности популяций в экологии чаще всего пользуются гистограммами, реже — линейными диаграммами. В Microsoft Excel гистограммы находятся в списке Стандартных диаграмм, для построения линейных диаграмм лучше пользоваться Гладкими графиками из списка Нестандартных диаграмм. Выбор зависит от качества представляемых данных. Учащиеся могут сделать выбор самостоятельно или действовать по заданию учителя. Ниже представлены различные варианты диаграмм. По оси абсцисс откладываем номер года, по оси ординат — численность популяции. Здесь важно еще раз вспомнить о биологическом смысле рассматриваемых задач: численность популяции не может быть меньше нуля, "номер" года также целое неотрицательное число, поэтому все диаграммы, отражающие динамику численности животных, должны располагаться в первой четверти координатной плоскости.

Диаграммы можно представить в нескольких вариан­тах. Например,

1.        Отобразить на одной координатной плоскости динамику численности оленей, полученную по результатам решения задач 1, 2 и 3 (см. рис.3).

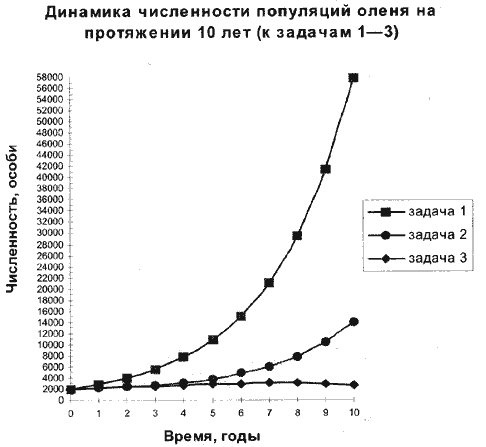
Рис. 3

2.        Отобразить на одной координатной плоскости изменения численности оленей по результатам всех пяти задач (см. рис. 4). Не забываем отбросить все отрицательные значения численности.

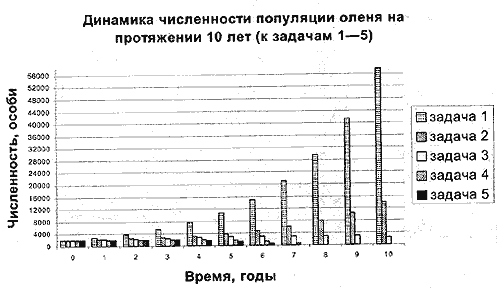
Рис. 4

3.        Отобразить численность жертв и хищников отдельно для каждой задачи. Трудность в этом случае заключается в подборе масштаба по оси ординат, так как популяция оленей насчитывает тысячи, а популяции волков и пум — десятки особей. Поэтому придется "растянуть" диаграмму как минимум до размеров листа А4, а лучше — до размеров листа A3. Можно поступить и по-другому: представить количество оленей в экспоненциальной форме, подобрав показатель степени так, чтобы мантисса была от 10 до 100. Тогда, например, в задаче 5 численность оленей в 0-й год будет рав­на 20 • 10², в 1-й год — 21 • 10², во 2-й год — 21,42 • 10² и т.д. Представляя численность жертв в виде мантиссы, мы искажаем диаграмму, но все же можем ее использовать для демонстрации соотношения динамики численности жертв и хищников (см. рис. 5).

 

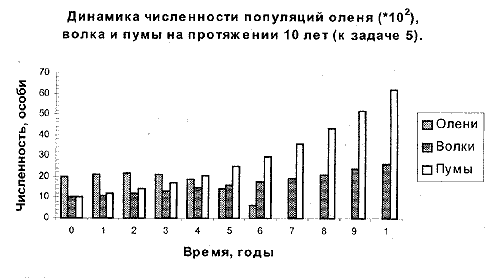
Рис.5

Обратите внимание на то, что, несмотря на полное вымирание оленей через 7 лет, количество хищников продолжает увеличиваться. Поскольку в условии ничего не сказано относительно других жертв волка и пумы, можно считать оленя единственной жертвой. Тогда рост численности хищников в отсутствие пищи объясняется ошибкой в построении модели. Аналогичную ситуацию можно наблюдать в задаче 4. Обратите также внимание на некоторые данные о численности волков, полученные в задачах 3—5 (см. рис. 2). В задаче 3 численность волков меняется так: 17, 18, 20, 22... особи; в задаче 4—17, 19, 21, 23.,. особи; в задаче 5—18, 19, 21, 24... особи, — и это при том, что годовой прирост численности волков одинаков во всех задачах. На этот раз ошибка вызвана округлением чисел. Обсуждение причин указанных ошибок поможет вывести учащихся на разговор об основных принципах составления математической модели природного процесса, а также о свойствах и назначении математического моделирования в целом. Не страшно, если ученики не смогут устранить ошибки. Важно, чтобы они научились анализировать данные, оценивать их достоверность и полноту.

Разобранное нами задание сформулировано и решено на примере оленя, волка и пумы, но это можно сделать и на примере других животных, вступающих в отношения "хищник—жертва" (мышь—лиса—рысь, заяц—волк—рысь и т.п.). Задание можно выполнить и в общем виде, обозначив "участников" как "жертва", "хищник-1" и "хищник-2". В последнем случае можно попросить учащихся самостоятельно подобрать подходящих животных. Увеличить разнообразие задач внутри задания можно, изменив одну или несколько констант в ячейках А1,.В1, С1, Dl, E1, G1, H1. Например:

 l. Al=2000; B1=0,4; C1=15;
    D1=20; Е1=0,1; G1=15; Н1=0,2.
 Тогда F1=11; 11=25; J1=16.

 2. А1=500; В1=0,8; С1=12; D1=15;
    Е1=0,2; G1=25; H1=0,4.
Тогда F1=3; 11=13; J1=7 (это возможно, так как Е1=0,2).

В качестве дополнительного задания можно попросить учащихся самостоятельно придумать несколько задач. Это могут быть новые вопросы к уже сформулированным задачам или задачи, основанные на минимальном изменении начальных данных.

Например, к задаче 2 можно задать вопрос:

Какова должна быть начальная численность волков, чтобы популяция оленей была стабильной в течение 5 лет?

Ответ подбираем в ячейке С1, следя за получаемыми значениями в ячейках С 5 : С 10. Ответ: 19.

Вопрос к задаче 3 может звучать так:

Каким должен быть годовой прирост популяции волков, чтобы численность оленей была относительно стабильна в течение первых 5 лет существования популяций?

Ответ подбираем в ячейке Е1, следя за получаемы­ми значениями в ячейках D5 : D10. Ответ: 0,2.

Условие дополнительного вопроса может быть дано в виде диаграммы. Например:

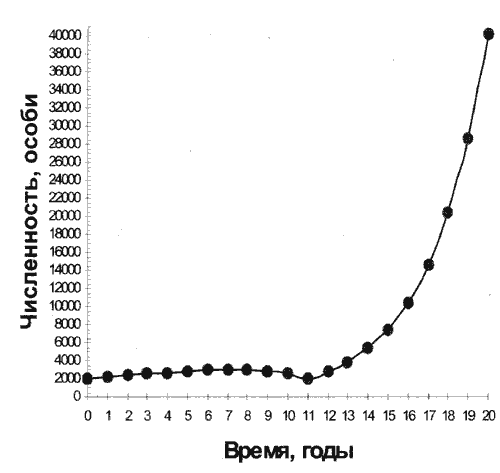
Рис . 6

 Изучите рис. 6. Объясните, при каких условиях возможны отображенные на рисунке изменения численности оленей. Предположите возможные последствия указанных изменений для существования сообщества.

Данные для этой диаграммы получены путем копирования формулы, записанной в ячейке D6, в ячейки D16:D25. Рост численности оленей с 11-го по 20,-й год возможен при исчезновении хищников.

К задачам 2 и 3 можно задать и более сложные вопросы, переходящие в ранг самостоятельных задач.

 Задача 2а

Как изменяется годовой прирост численности оленей в течение 10 лет при сохранении всех условий задачи 2? Отобразите результат графически.

Задача 3а.

Как изменяется годовой прирост численности оленей в течение 10 лет при сохранении всех условий задачи 3? Отобразите результат графически.

 Для того чтобы решить эти задачи, необходимо определить, что такое "годовой прирост численности популяции" .

Годовой прирост численности представляет собой разность рождаемости и смертности в популяции. Рождаемость определяется как доля рожденных за год по отношению к численности популяции на начало года. Смертность, соответственно, определяется как количество умерших в течение года по отношению к численности популяции на начало года. В данном случае удобнее пользоваться не относительными значениями рождаемости и смертности, а абсолютными количествами рожденных и умерших за год. Тогда годовой прирост будет вычисляться следующим образом: 

Годовой прирост популяции = ( количество рожденных за год — количество умерших за год) /  численность популяции на начало года

Решения

По условию задач 2 и 3 гибель оленей происходит только по вине волков и составляет 30 особей на 1 вол­ка в год.

 

Задача 2а

1.         Начиная решать задачу, необходимо убедиться, что в ячейках А1, В1, С1, Dl стоят числа, соответствующие условию задачи 2.

2.         Используем новый столбец L, В L5 заносим формулу =( (C5-$C$1*$D$1) *$B$1-$C$1*$D$1) /С5.

3.         Копируем формулу в ячейки L6:L15 и строим диаграмму (см. рис. 7).

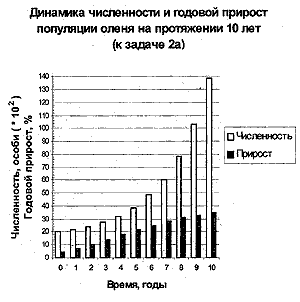
Рис. 7

Задача 3а

1. Для решения задачи используем столбец М. Записываем формулу в ячейку

М =((D5-H5*$D$1)*$B$1-H5*$D$1)/D5.

2. Копируем формулу в ячейки М6:М15 и строим диаграмму (см. рис. 8).

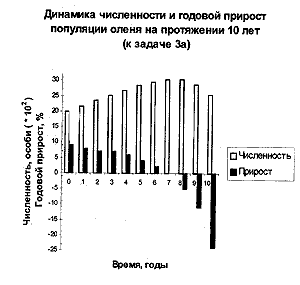
Рис. 8

На рис. 7 и 8 значения численности оленей представлены в экспоненциальной форме в виде числа, умноженного на 10², поэтому диаграммы искажены. Несмотря на это, диаграмма к задаче 2а дает нам возможность показать учащимся различие в скорости изменения годового прироста популяции и ее численности. Диаграмма к задаче 3а показывает, что годовой прирост популяции бывает как положительным, так и отрицательным, при том, что численность популяции — число всегда положительное. Этот момент, как ни странно, зачастую вызывает затруднения у ребят.

Численность и годовой прирост лучше было бы отложить на разных вертикальных осях. В списке Нестандартных диаграмм в Microsoft Excel имеется Двухосевой график, но мы не можем использовать его для построения линейной диаграммы, поскольку в этом "графике" начало координат по горизонтальной оси не совпадает с 0 по вертикальным осям. Кроме того, гистограммы в данном случае более уместны, нежели линейные диаграммы.

Решение дополнительных задач вносит изменения в электронную таблицу, выполненную учащимися дома. Эти изменения могут вызвать путаницу во время презентации, так как не все дети могут быстро сопоставить старые результаты с новыми. Чтобы избежать этого, достаточно предложить учащимся скопировать "домашнюю" таблицу на другой (второй) лист того же документа и выполнять все дополнительные вычисления на этом листе. Дополнительные вопросы и задачи предназначены для контроля за усвоением учащимися материала, включенного в проект.

Хорошо, если в школе имеются технические возможности для проецирования изображения с монитора компьютера на большой экран. Если таких возможностей нет, можно распечатать полученные диаграммы на прозрачную пленку и демонстрировать их с помощью кодопроектора. Если и такой возможности нет, можно попросить учащихся изобразить диаграммы на заранее подготовленных листах ватмана, на кодопленке или на доске. Таким же образом можно подготовить иллюстративный материал к презентации работы, выполненной дома. Наглядность необходима для вовлечения всего класса в обсуждение результатов решения, и учителю важно добиться, чтобы все учащиеся в конце концов пришли к верному результату. Момент наглядности особенно необходим, если учителя решились на совместную работу. Выполняя описанное задание без участия учителя биологии, учитель информатики может вообще обойтись без презентации и разобрать результаты решения задач традиционным способом. Однако даже в этом случае обращение к экологической тематике на уроках ОИВТ позволяет "встряхнуть" ребят, показать им, как можно применять информационные технологии для решения проблем, связанных с живой природой. Это не только полезно для учащихся, но и значительно оживляет процесс обучения и делает более интересной работу самого учителя.