Моделирование и элементы системологии
Учебное пособие для учащихся 11-х классов
Т.П.Чубарова
Введение
Каждый из нас в своей жизни неоднократно сталкивается с какими-либо проблемами, и поэтому каждому приходится принимать определенные решения.
По какой дороге везти груз? Какой суп сварить на обед? Какой построить садовый домик? Одним словом, нам часто приходится принимать решения и на работе, и дома. Ну а для руководителей любого ранга решения — это основной вид продукции. Каждый, кто сталкивался с решением сложных проблем, с принятием деловых или личных решений, знает, насколько это сложно и сколько сил на это требуется.
Задачи такого типа не рассматриваются ни на одном из школьных предметов, все это — "жизненные задачи".
Принимая решение, руководитель предприятия, врач, военачальник наряду с количественными результатами должен учитывать множество обстоятельств и соображений. В результате решение не сводится к однозначным ответам. Как правило, получается, что в одинаковых условиях можно действовать и так, и иначе. А жизнь заставляет на чем-то остановиться, прийти к вполне определенному, единственному решению. Тут не обойтись без выбора, который, помимо умения считать, требует еще и волевых качеств.
Французский ученый, физик и логик, ректор Парижского университета Жан Буридан (ок. 1300 — ок. 1358) сочинил притчу об осле, который умер с голода, так как не смог выбрать одну из двух одинаковых охапок сена, оставленных ему хозяином. Печальная история буриданова осла — лучшая иллюстрация того, что может приключиться, если у принимающего решение отсутствует воля.
В век научно-технической революции условия человеческой деятельности и связанные с ней решения небывало усложнились. Рассчитывать при принятии решения только на опыт и интуицию уже нельзя. Полагаться в решении такой задачи на "озарение" — это значит заранее обречь себя на неудачу.
Все "жизненные задачи" являются плохо поставленными задачами, т.е. из их условия нельзя однозначно извлечь, что является исходными данными, а что — результатами, а также — какова связь между ними. К примеру, задание "Решить уравнение 2x + 3 = 7", конечно, является задачей (возможно, для кого-то и весьма трудной), но не является плохо поставленной задачей, так как в ней абсолютно ясно, что дано, что надо найти и какова связь между исходными данными и результатами. Точно так же любая текстовая задача из учебника математики (да и практически любого другого предмета) — это хорошо поставленная задача.
Оказывается, для решения самых разнообразных жизненных, плохо поставленных задач существуют специальные методы и подходы, которые позволяют выбрать более правильное решение, добиться лучших результатов при тех же затратах. Любые методы, которые помогают человеку понять, что он хочет и что у него есть, которые позволяют оценить с единых позиций желаемые цели и имеющиеся ресурсы, являются не только полезными, но порой и просто необходимыми.
Разобраться с методами решения "жизненных" задач нам поможет наука системология, которая направлена на решение "жизненных задач", на выяснение причин сложностей, возникающих при решении какой-либо проблемы.
Вопросы и упражнения
1. Что такое хорошо поставленная и плохо поставленная задача? В чем их отличие? Приведите примеры хорошо и плохо поставленных задач. 2. Приведите пример, когда одна жизненная задача допускает несколько решений.
Понятие системы
Системность есть всеобщее свойство
материи.
Ф.И. Перегудов, Ф. П. Тарасенко
Как понятно из названий, системология и системотехника произошли от слова "система". С этим словом вы встречались неоднократно. Вам знакомы такие понятия, как "система кровообращения", "нервная система", "система водоснабжения города", "система связи", "периодическая система элементов Д. И. Менделеева", "системы счисления" и т.д. В последнее время слово "система" встречается практически в каждой науке или технической книге. Что же такое система?
Вообще говоря, понятие "система" относится к числу основных, т.е. лежащих в основании теории, а поэтому оно может быть лишь описано через синонимы и пояснено примерами.
Термин "система" в переводе с греческого означает целое, составленное из частей, или соединение частей в целое. Таким образом, система состоит из отдельных частей — элементов, причем эти элементы взаимосвязаны. Характеристики системы определяются не столько характеристиками ее элементов, сколько характеристиками взаимосвязей. Одни и те же элементы, в зависимости от объединяющей их взаимосвязи, могут образовывать различные по своим свойствам системы, как, например, из одних и тех же кирпичей можно складывать самые различные сооружения. Поэтому любая система характеризуется элементами и связями между ними.
Под системой понимают единство связанных друг с другом предметов и явлений в природе и обществе.
Рассмотрим примеры систем. Любой живой организм является системой. Действительно, он состоит из отдельных, тесно взаимосвязанных частей. Разбери живой организм на отдельные части, и его не будет. Живые организмы, в свою очередь, тоже объединяются в систему. 06 экосистемах вы неоднократно говорили на уроках экологии. Люди тоже объединяются в системы. Например, системой можно считать ученический коллектив класса, школы или целое государство. Системой является и наша Вселенная, так как все звезды, все планеты взаимодействуют друг с другом. Системой является обычный самолет. Произойди поломка какой-либо одной из его частей, и может произойти авария.
Система в целом качественно отличается от суммы составляющих ее частей, имеет свойства, которых нет у ее элементов. Причем эти новые свойства определяются именно взаимосвязями элементов. Объединим, например, в систему вас и стереомагнитофон с колонками. Чтобы добиться стереоэффекта, нужно определенное взаиморасположение вас и звуковых колонок. Если же вы расположитесь в одну линию с колонками, то стереоэффект пропадет.
Природа элементов, входящих в систему, может быть самой разнообразной. Элементами могут быть:
• материальные объекты (небесные тела, детали станка и т.д.);
• субъекты (рабочие, служащие, анатомические органы живых существ и т.д.);
• идеальные объекты (системы аксиом, система основных понятий механики, проект технологических линий и т.д.).
Системы бывают как искусственными, созданными руками человека (например, самолет, завод, система счисления), так и естественными. Примерами естественных систем могут служить кристаллы, Солнечная система, живые организмы.
Вопросы и упражнения
1. Что такое система?
2. Приведите примеры известных вам систем.
3. Назовите две основные характеристики системы.
4. Какую роль в системе играют взаимосвязи элементов ?
5. Покажите на примерах, что система в целом качественно отличается от суммы составляющих ее частей.
6. Какова природа элементов, входящих в систему? Приведите примеры для каждого из типов элементов.
7. Существуют ли системы, в которые входят элементы разной природы одновременно? Если "да", то приведите примеры, а если "нет", то объясните, почему.
8. Приведите примеры биологических систем.
9. Приведите примеры общественных систем.
10. Приведите примеры технических систем.
11. Является ли системой живая клетка?
12. Является ли системой груда разбросанных кирпичей? А стена, сложенная из этих кирпичей?
13. Является ли системой квартира?
14. В чем различие искусственных и естественных систем?
15. Как вы считаете, может ли какой-либо объект или явление быть несистемным?
Системы, надсистемы, полсистемы
Определив систему, мы как бы проводим условную замкнутую границу, за которой остаются не вошедшие
в систему элементы. Например, в предыдущем параграфе за границами системы остались все посторонние звуки, хотя эти звуки тоже каким-либо образом могут влиять на нашу систему.Множество существующих вне системы элементов, которые оказывают влияние на систему, или, наоборот, на которые воздействует система, называют внешней средой системы. Если мы возьмем в качестве системы ученический коллектив одного класса, то весь остальной коллектив школы будет относиться к внешней среде нашей системы.
Граница между системой и ее внешней средой очень условна. Наличие связей между элементами системы и элементами внешней среды часто затрудняет определение границ системы. Формального способа определения границ системы не существует.
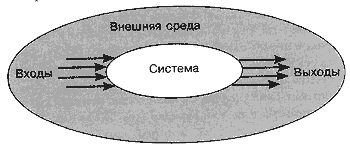
Итак, система связана с окружающей средой: среда
воздействует на систему и система воздействует на среду. Связи, с помощью которых внешняя среда воздействует на систему, называют входами системы, а связи, с помощью которых система воздействует на среду называются выходами системы. На рис. 1 эти связи изображены стрелками.
Рис. 1. Взаимодействие системы и внешней среды
Любая система, в свою очередь, может являться элементом другой системы более высокого уровня, которая будет являться для нашей системы внешней средой и которая называется надсистемой, или метасистемой. Если принять за систему какой-либо класс, состоящий из учеников, то школа, состоящая из классов и педагогического состава, может являться для него системой более высокого уровня (надсистемой). Школа, в свою очередь, может являться элементом системы образования города и т.д. Класс, в очередь, является элементом системы "школа", а школа является элементом системы образования города.
Если элементы какой-либо системы сами являются системами, то их обычно называют подсистемами данной системы, а ее трактуют как общую систему. Каждая общая система по отношению к ее элементам и подсистемам является надсистемой (метасистемой). Практически все элементы любой системы можно рассматривать в качестве ее подсистем. В этом смысле каждая система является составляющей некоей надсистемы.
Сложность такого положения заключается в том, что не ясно, до какого предела систему можно разбивать на подсистемы, а также образовывать метасистемы (например, станок состоит из отдельных узлов, каждый узел состоит из отдельных деталей, каждая деталь состоит из молекул, каждая молекула состоит из...; и наоборот, отдельный станок является частью всех станков цеха, все станки цеха являются составляющей материальной части цеха и т.д.). Другими словами, остается открытым вопрос о существовании минимальной подсистемы и максимальной метасистемы по отношению к любой системе. Однако такая неопределенность философского плана не мешает пользоваться понятием системы в конкретных научных дисциплинах.
Договоримся те части системы, которые нам удобнее рассматривать как неделимые, называть элементами системы, а те части системы, которые мы будем рассматривать как составленные из других частей, называть подсистемами.
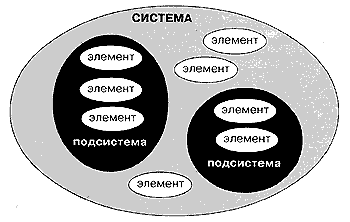
Рис. 2. Состав системы
При рассмотрении систем важно учитывать положение о всеобщей взаимозависимости и взаимосвязанности явлений. Любой элемент, любая подсистема испытывает на себе влияние не только системы, но и метасистемы. Так, если рассматривать ученический коллектив класса как систему, то на элементы этой системы — учащихся класса — оказывает влияние и надсистема — школа в целом.
В то же время нельзя забывать, что свойства системы в значительной степени определяются ее элементами. В нашем примере коллектив класса зависит от каждого учащегося данного класса.
Таким образом, система не может рассматриваться изолированно, вне связей с надсистемами, система зависит от свойств надсистем.
Системы более высокого уровня сложнее своих подсистем. С повышением уровня система приближается к общегосударственным, общенациональным интересам или к интересам всего человечества. На такую систему влияет очень большое число сложных и разнообразных факторов, которые очень трудно учесть.
Вопросы и упражнения
1. Что такое внешняя среда системы? Приведите примеры.
2. Что такое входы и выходы системы? Приведите примеры.
3. Что такое подсистема? Приведите примеры систем, элементами которых являются подсистемы.
4. Что общего между системами, надсистемами, подсистемами? В чем разница между ними?
5. Приведите примеры систем и укажите, что для них будет являться надсистемами и подсистемами.
6. Какие части системы называют ее элементами и какие подсистемами?
7. Покажите на примерах, как на элементы системы воздействует надсистема.
Сложность систем
Рассмотрим некоторую систему, состоящую из N элементов. Тогда количество возможных взаимосвязей между ними выражается числом N • (N — 1). Это следует из того, что между любыми ее двумя элементами существуют две связи — прямая и обратная, которые могут не совпадать друг с другом.
Те системы, в которых количество связей относительно невелико, обычно называют простыми системами. Те же системы, в которых очень большое количество связей, называют сложными системами.
Обычно различают три типа сложных систем. К первому относятся системы с четко выраженной иерархией (соподчиненностью). Сложные системы первого типа поддаются математическому описанию. Системы такого типа будем называть не очень сложными системами. К не очень сложным системам можно отнести, например, телефонную сеть какого-либо города.
Ко второму типу относятся системы, которые не поддаются строгому математическому описанию, либо те системы, для которых математический аппарат еще не разработан. Системы такого типа будем называть очень сложными системами. К ним можно отнести, например, нашу планету в целом.
К третьему типу сложных систем причисляют такие, в которых отчетливо просматривается присутствие "человеческого фактора", обладающего своими, скрытыми, целями. Каждый человек имеет свои личные цели, которые далеко не всегда совпадают с целями системы, в которую они входят. Часто эти цели не ясны другим людям, и прежде всего руководителям системы. Поэтому часто такие системы оказываются неэффективными и их цель не бывает достигнута вообще или в полной мере. Чтобы такие системы были эффективными, необходимо учитывать и интересы входящих в эту систему людей. Если руководитель некоего предприятия не будет учитывать интересы своих работников, не будет заботиться о них, то такое предприятие не сможет работать достаточно эффективно. Системы третьего типа будем называть сверхсложными системами.
Заметим, что система, включающая небольшое количество людей, вообще говоря, имеет немного связей, но она будет сверхсложной системой. Поэтому следует сделать уточнение: простыми будем называть те системы, в которых количество связей относительно невелико и нет ярко выраженного человеческого фактора.
Важно отметить, что простые и сложные системы подвергаются научному исследованию, а для сверхсложных систем соответствующий исследовательский аппарат еще не разработан.
Заметим также, что предложенная классификация систем по степени сложности не является достаточно полной и строгой.
Вопросы и упражнения
1. Какие системы являются простыми? Приведите примеры простых систем.
2. Подсчитайте максимально возможное число связей в системе, состоящей из 10 элементов.
3. На какие типы можно разделить сложные системы?
4. Приведите примеры каждого из типов сложных систем.
5. Как вы считаете, является ли сложной система, объединяющая трех подруг?
6. К какому типу систем вы отнесете компьютер? нервную систему человека? семью? токарный станок? дерево? Ответ поясните.
Что изучает системология? Место системологии среди других наук
С конца 30-х годов системы являются предметом исследования математиков, рассматривающих "системы вообще" в различных предметных областях. Во второй половине нашего столетия появляется ряд новых научных направлений, таких, как кибернетика, математическая теория систем, теория принятия решений, исследование операций и искусственный интеллект. Все эти направления тесно связаны с возникновением компьютерных технологий, и все они связаны с понятием системы.
Естественно, возник вопрос: а нельзя ли смотреть на эти научные направления как на части общей науки о системах? Идея построения теории, которая бы занималась системами любой природы, принадлежит австрийскому биологу Людвигу фон Берталанфи (1901—1972). Эта наука и называется системологией.
Системология, или системный анализ, — это наука об общих принципах организации сложных систем, это анализ очень сложных объектов, из-за сложности которых трудно изучать протекающие внутри них процессы и тем более их контролировать. Системология позволяет по косвенным признакам прогнозировать те или иные процессы и управлять ими.
Лабораторией для науки о системах является компьютер, который позволяет экспериментировать ученому-системщику точно так же, как это делают другие ученые в своих лабораториях.
Системология далеко вышла за рамки математики. Уже не только ученые, но и люди самых различных профессий (инженеры, предприниматели, педагоги, деятели культуры) обнаружили системность своей деятельности.
Мы с вами будем говорить не только о естественных системах, созданных самой природой, но и об искусственных системах, созданных руками человека. Создать хорошо отлаженную систему, особенно сложную, довольно трудно. Это целая наука. О том, как правильно создавать системы, мы узнаем при знакомстве с элементами системологии.
Можно выделить два основных направления научного развития.
Первое направление состоит в следующем. Для того чтобы понять тонкости, лежащие в основе явления, стремятся проникнуть вглубь изучаемого явления, оно искусственно расчленяется, и каждая часть рассматривается отдельно, без учета влияния извне. Изучением каждой из этих частей занимаются специальные научные дисциплины.
Мы привыкли к традиционному делению наук на физику, химию, биологию, социологию и т.д. На рис. 3 предметная "нарезка" знаний представлена вертикальными линиями. Предметом любой научной дисциплины является определенный класс систем.
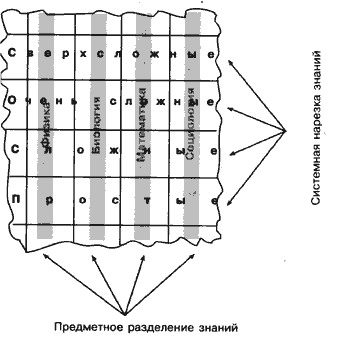
Физика изучает одни свойства предметов и явлений, химия — другие, биология — третьи, социология — четвертые... Обычно эти предметы и явления представляют собой сложные системы со множеством связей. Но мы уже говорили о том, что система в целом качественно отличается от суммы составляющих ее частей и имеет свойства, которых нет у ее элементов. Яблоко, например, с точки зрения химии — это набор химических элементов, с точки зрения физики — это предмет, который имеет определенную массу и низкую электропроводность, с точки зрения биологии — это плод и т.д. И тем не менее это яблоко, имеющее свойства, присущие только ему.
Другое направление возникло благодаря намерениям исследователей добиться результатов, характеризующих явление в целом. В этом случае могут игнорироваться некоторые особенности, глубина результата, но выявляются общие свойства, которые характерны для групп
явлений, фактов, закономерностей и т.д. Другими словами, достижения научных дисциплин обобщаются.Системный подход базируется как раз на том, что к предмету или явлению нужно относиться как к системе, что они могут проявить свои системные свойства. Само явление здесь рассматривается как элемент некоторой системы с учетом взаимосвязей с другими явлениями, что позволяет выделить основные свойства явлений. Они, как правило, носят междисциплинарный характер
Системный подход позволяет охватить изучаемый предмет или явление в целом — с учетом разнообразных
связей, присущих только ему. В первую очередь на системный подход опираются те дисциплины, для которых недостаточно разработан исследовательский аппарат.Системология предполагает "горизонтальное" разделение знаний, т.е. делит все знания не на предметы, а по уровню
сложности знаний — на простые, не очень сложные, сложные и сверхсложные. Таким образом, привычному разделению наук противопоставляется объединение наук.Из этого следует, что системологию нельзя сравнивать с другими науками. Более правильно рассматривать ее как новое измерение в науке.
Вопросы и упражнения
1. Что такое системология?
2. Назовите несколько наук, родственных системологии.
3. Какую роль в работе ученых-системщиков играет компьютер?
4. Почему один и тот же объект, предмет или явление может изучаться в разных дисциплинах?
5. Приведите примеры, когда одно и то же явление рассматривается разными научными дисциплинами с разных сторон.
6. В чем состоит системный подход в изучении объектов, процессов и явлений?
7. В чем разница между традиционным подходом к изучению объектов, процессов и явлений и системным подходом?
Что такое модель?
При поступлении на работу обычно каждый человек заполняет личный листок по учету кадров. Эта анкета — модель человека: она отражает какие-то его черты. Когда человек ложится в больницу, заполняется "история болезни" — анкета, в которой некоторые пункты совпадают хоть и с пунктами в личном листке, но обязательно имеются и другие, специфические. Наконец, того же гражданина может задержать милиция и составить на него протокол — модель для предъявления обвинения.
Таким образом, один и тот же объект может быть описан множеством моделей. Каждая из этих моделей дает лишь какое-то представление о самом объекте.
Но каким бы ни было описание человека, это все равно не сам человек. Обычно в любой своей деятельности человек всегда создает модель того объекта, процесса или явления, с которым ему приходится иметь дело.
Можно сказать, что модель — это некий заменитель объекта, процесса или явления, который в определенных условиях может заменять оригинал, воспроизводя интересующие нас свойства и характеристики оригинала. Причем модель имеет существенные преимущества и удобства (наглядность, обозримость, доступность испытаний, легкость оперирования с ними и т.д.). Иначе говоря, модель — это некоторое упрощенное подобие реального объекта, процесса или явления.
Модели значительно облегчают понимание системы, позволяют проводить исследования в абстрактном плане, прогнозировать поведение реальной системы в интересующих нас условиях. Основное назначение и преимущество модели заключается в том, что в ней сконцентрированы важные факторы реальной системы, которые подлежат изучению в конкретном исследовании. Несущественные факторы либо отсутствуют в модели, либо отражены в ней в небольшой степени. Исключение несущественных факторов не просто упрощает модель и облегчает ее построение, оно является немаловажным преимуществом модели. Их наличие в реальном объекте мешает исследователю, создает некоторый "шум", помехи, на фоне которых труднее выявить необходимые свойства и закономерности.
Наиболее важное преимущество модели — возможность простыми средствами изменять ее параметры, вводить некоторые воздействия с целью изучения реакции системы. В реальных условиях получить аналогичные сведения значительно труднее и дороже, а иногда и просто невозможно (например, изучить работу системы в аварийных условиях).
Использоваться могут различные виды моделей. Простейшими являются масштабные, или натурные, модели, в которых соблюдается геометрическое подобие оригинала. Это может быть карта, глобус, модель кристаллической решетки. Громоздкие объекты (корабли, самолеты, здания) представляются обычно в уменьшенном виде, а мелкие (атомы, молекулы), наоборот, в сильно увеличенном.
В аналоговых моделях исследуемые процессы заменяются процессами, которые имеют другую физическую природу, но описываются теми же математическими соотношениями. Например, колебания груза на пружине аналогичны колебаниям тока в электрическом контуре.
Информационная модель — это информация (т.е. знания, сведения) о реальном объекте, процессе, явлении. Представьте себе, что вам подробно описали внешность человека, которого вы никогда не видели. Затем по описанию вы узнали этого человека. Стало быть, в вашем сознании сложился некоторый образ человека в результате сообщенной информации, т.е. создалась информационная модель.
Наиболее мощным средством исследования систем являются математические модели. Построение математической модели начинается с описания исходных данных и результатов, а затем на основании изучения реальной системы устанавливают виды взаимосвязи между исходными данными и результатами, формальная запись этих зависимостей и дает математическую модель.
Анализировать математические модели проще и быстрее, чем экспериментально определять поведение реального объекта в различных режимах работы. Кроме того, анализ математической модели позволяет выделить наиболее существенные свойства данной системы, на которые надо обратить особое внимание при принятии решения.
Чтобы модель можно было хорошо изучить и проводить с нею эксперименты, она сама должна быть достаточно простой. Однако чем проще модель, тем обычно в меньшей степени она соответствует моделируемому процессу или объекту. Поэтому моделирование всегда компромисс между простотой модели и обеспечиваемой ею точностью.
Вопросы и упражнения
1. Что такое модель?
2. В чем принципиальное отличие модели от моделируемого объекта?
3. Для чего человек часто заменяет объекты, процессы или явления их моделями?
4. Какие виды моделей вы можете назвать? Дайте краткую характеристику каждому из этих видов.
5. Могут ли разные явления описываться одной и той же моделью? Приведите примеры.
6. Можно ли для одного и того же объекта, процесса, явления построить несколько различных моделей? Если да, то приведите примеры.
7. Рассмотрите в качестве явления какую-нибудь мелодию. Постройте для нее модель.
8. Можно ли считать литературное произведение моделью? Почему?
Моделирование как неотъемлемая часть системологии
Моделирование играет огромную роль при подготовке принятия решения. В жизни практически никогда не бывает совершенно одинаковых ситуаций, поэтому принимать решение приходится в условиях неполной и недостаточной информации. В таких случаях недостаточную информацию пытаются получить, используя предположения, результаты научных исследований, полученных путем изучения соответствующих моделей. Для успешного управления системой необходимо предсказывать ее поведение в будущем, а это можно сделать, исследуя интересующие нас свойства на моделях.
Любая деятельность человека, создание любой системы направлены на достижение определенной цели. Цель является образом того, что мы хотим достичь, т.е. цель — это модель будущего состояния системы (описательная модель). Описательная модель отвечает на вопрос "что мы хотим делать?".
Наша деятельность, направленная на достижение этой цели, осуществляется по определенному плану или по определенному алгоритму. Этот алгоритм мы должны придумать заранее, так как мы должны составить модель наших действий (алгоритмическую модель). С помощью алгоритмической модели можно сравнить последствия всех наших возможных действий, не выполняя их реально, как говорят, "проиграть" их на модели. Алгоритмическая модель отвечает на вопрос "как мы будем делать?".
Таким образом, моделирование является неотъемлемой частью любой целенаправленной деятельности, в том числе и деятельности, направленной на создание систем.
Как вы уже поняли, один и тот же объект может быть описан различными моделями. Выбор модели зависит от того, какие мы ставим перед собой цели, для решения каких задач эта модель предназначена (вспомните пример с моделями человека в отделе по учету кадров, в больнице и в милиции). Изменение цели непосредственно влечет за собой и изменение модели. Если мы хотим сделать обеденный стол, то в нашем воображении мы нарисуем этот стол. Но если мы передумаем и решим делать письменный стол, то в нашем воображении это будет совсем другой стол, и соответственно изменится алгоритм, по которому мы будем его делать.
Модели получатся разные, в зависимости и от того, какие факторы считаются важными, а какие второстепенными, какие упрощающие предположения были сделаны. Пусть мы хотим описать движение тела, брошенного под углом к горизонту. Можно сделать упрощающие предположения: тело является материальной точкой, сопротивление воздуха мало и им можно пренебречь, ускорение свободного падения постоянно и т.п. В этом случае мы получим уравнения, известные вам из курса физики. Если же мы решим учитывать сопротивление воздуха или какие-либо другие факторы, влияющие на движение тела, то получим другие уравнения.
От цели моделирования зависит, какие свойства объекта включать в модель, а какие нет. Пусть мы создаем модель некоего мужчины. Если мы хотим, чтобы наш знакомый нашел этого мужчину среди других, то мы включим в описательную модель его примерный рост, цвет волос и еще какие-то отличительные черты его внешности. Если же модель предназначена для его лечащего врача, то описывать мы будем скорее всего не внешность, а состояние его здоровья.
Таким образом, цель моделирования определяет, какие стороны оригинала должны быть отражены в модели. Для различных целей требуются различные модели одного и того же объекта. Модели можно условно разделить на две группы:
1. Модели, которые строятся для изучения какого-либо уже существующего процесса или явления (модель ядерной реакции или модель атомного ядра).
2. Модели для создания будущих процессов или явлений (планы и программы действий, модель управления производством, модель строящегося дома).
Модели первой группы — это познавательные модели, которые отражают уже существующие системы. А модели второй группы — это так называемые прагматические модели, которые отражают еще не существующие, но желаемые системы.
Разделение моделей на эти две группы условно, поскольку существует множество моделей, которые трудно отнести к одной из этих групп, например, произведения искусства или медицинские модели.
Можно подойти к делению на группы по другому принципу. Для некоторых целей нам могут понадобиться модели, которые не изменяются во времени. Например, фотография какого-либо объекта, чертеж детали и т.д. Такие модели называют статическими. Для других целей нам могут понадобиться модели, которые изменяются во времени, — так называемые динамические модели. Это, например, модель развития популяции живых организмов, модель ядерной реакции и другие.
Вопросы и упражнения
1. Чем при принятии решения может помочь моделирование?2. В чем отличие описательных и алгоритмических моделей?
3. Покажите на примерах, что для различных целей требуются и различные модели одного и того же объекта.
4. В чем будут, по-вашему, различия в моделях лошади, с точки зрения крестьянина, жокея, скульптора, повара?
5. В чем разница между познавательными и прагматическими моделями?
6. Почему карту местности можно отнести и к познавательным, и к прагматическим моделям?
7. В чем различие между статическими и динамическими моделями? Приведите примеры.
Структура системы
Напомним, что под системой мы понимаем единство взаимосвязанных предметов и явлений в природе и обществе. Поэтому система характеризуется как своим составом, так и своей структурой, т.е. взаимосвязями ее элементов и их соподчиненностью (иерархией). Иерархия означает, что элементы каждой системы связаны друг с другом и что среди них находятся главные (определяющие, ведущие) и соподчиненные им (определяемые, ведомые ими) элементы.
Структурирование системы заключается в установлении иерархии между элементами системы и их взаимосвязей. Общих правил определения в системе главных элементов и их взаимосвязей не существует.
Структуру системы можно описать различными способами.
Часто используется иерархическая структура типа "дерево". Применение этой структуры возможно, когда все подсистемы строго соподчинены своим надсистемам.
Рассмотрим для примера структуру некоего института. Для простоты предположим, что в институте всего три факультета: физический, химический и биологический. На физическом факультете три кафедры: общей, теоретической и экспериментальной физики. На химическом факультете всего две кафедры: кафедра органической и неорганической химии. А на биологическом факультете есть кафедры ботаники, зоологии и анатомии.
Системы в дереве разделены на уровни. На первом уровне находится самая сложная система, которая называется корнем дерева. На втором уровне — три ее подсистемы (три ветви), которые подчинены всей системе. В свою очередь, каждая система второго уровня разбита на соответственно подчиненные им подсистемы. Системы самого нижнего уровня называют листьями. По линиям связи дерева легко определить, какая кафедра какому факультету принадлежит. Аналогично отражена принадлежность факультетов институту.
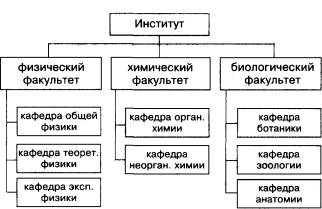
Рис. 4. Структура типа "дерево"
В дереве соотношения между верхними и нижними уровнями имеют характер "один ко многим".
Для наглядности структуру системы можно изобразить геометрически. Для этого ее элементы изображают чаще всего плоскими геометрическими фигурами. При этом главные элементы можно изображать в верхней части схемы, а соподчиненные — под ними. Связи между элементами изображают стрелками или отрезками.
Может оказаться, что некоторые из элементов окажутся соединенными сразу с несколькими (а может, и со всеми сразу), а другие только с одним из элементов. Получается соотношение "многие ко многим". В этом случае используется сетевая структура. Примером может служить посещение факультативов разными учащимися, когда они посещают по нескольку факультативов.
На рис. 5 хорошо видно, какие факультативы посещают какие ученики.
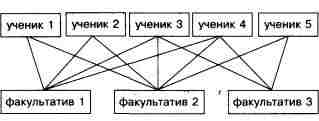
Рис. 5. Сетевая структура
Структуру системы часто бывает удобно представить в виде таблицы.
В таком виде удобно описать, например, систему движения самолетов.
Табличные структуры являются наиболее распространенными, и к ним можно свести другие рассмотренные виды структур. Кроме того, для работы с ними разработан мощный математический аппарат, что позволяет достаточно эффективно работать с ними на ЭВМ.
|
Аэропорт назначения |
Номер рейса |
Тип самолета |
Дни отправления |
Время отправления |
|
Адлер |
302 |
Ту-154 |
1,4,6 |
14-30 |
|
Киев |
320 |
Ту-154 |
2,3 |
20-45 |
|
Новосибирск |
280 |
АН-24 |
1,4,7 |
13-00 |
Табличная структура
То есть если в рассматриваемой системе четко выражена иерархия, то ее модель можно построить несколькими способами.
В обобщенном виде модель структуры с четко выраженной иерархией строится так.
Пусть система S
разбита на несколько подсистем. Пусть для
определенности она разбита на 4 подсистемы:
S1, S2, 53, S4.
Обозначим через &1 связи между этими
подсистемами. Тогда
S == {S1, S2, S3, S4, &1}.
Пусть система S1, в
свою очередь, состоит из подсистем S11,
S12, S13.
Связи между этими подсистемами обозначим
через &2. Тогда
S1
= {S11l, S12, S13, &2}.
Аналогично запишем для других систем:
S2
== {S21, S22, S23, S24, S25, &3}.
S3
= {S31, S32, S33, &4}.
S4
= {S41, S42, S43, S44, &5}.
Если, в свою очередь, системы S11, S12 и т.д. разбиваются на подсистемы, то нужно и для них сделать соответствующие записи.
Полученная модель называется кортежной. Кортежная модель не очень наглядна.
Информационные структуры, содержащие взаимосвязанные данные о реальных объектах и хранящиеся во внешней памяти ЭВМ, называются базами данных (БД). Базы данных — это хранилища информации.
Чтобы работать с базами данных, нужно специальное программное обеспечение. Оно носит название системы управления базами данных (СУБД). С помощью СУБД строятся базы данных и производится работа с ними.
Обычно СУБД ориентируются на определенные типы структур данных. Наибольшее распространение получили так называемые реляционные СУБД, ориентированные на работу с таблицами.
Вопросы и упражнения
1. Что понимают под структурой системы?
2. Что значит "структурировать систему" ?
3. Какие способы описания структуры системы вы знаете?
4. Когда следует представить структуру системы в виде дерева и когда в виде сети?
5. Представьте структуру какой-либо системы в виде кортежной модели.
6. Представьте структуру какой-либо системы в виде дерева.
7. Представьте структуру какой-либо системы в виде сети.
8. Представьте структуру какой-либо системы в виде таблицы.
9. Возьмите в качестве системы все предметы, изучаемые в школе. Постройте для нее три модели: в виде дерева, в виде сети и в виде таблицы.
10. Что такое базы данных?
11. Что такое СУБД? Для чего они предназначены?
12. Какие СУБД называются реляционными?
Черные ящики
Часто случается, что для изучения системы не обязательно знать ее внутреннее устройство, а иногда это внутреннее устройство бывает просто неизвестно. Например, чтобы научиться пользоваться телевизором, нам совсем не обязательно знать, как он устроен. Мы еще не очень хорошо знаем, как устроен мозг человека, но мы можем изучать, какое воздействие оказывает на него то или иное лекарство.
Объект, устройство которого скрыто от исследователя, называют "черным ящиком".
Модель "черного ящика" изображена на рис. 6. Отказ от изучения и моделирования внутренней структуры объекта часто упрощает исследование этого объекта. Надо отметить, что если внутреннее устройство "черного ящика" для нас неизвестно или неважно, то наличие входов и выходов играет важную роль.

Рис. 6. Модель "черного ящика"
"Черные ящики" можно разделить на две группы. Если при одинаковых воздействиях на "черный ящик" (при одинаковых значениях на входах) мы всегда получаем одинаковый результат (одинаковые значения на выходах), то такой "черный ящик" называют функцией. "Черные ящики" такого типа действительно похожи на функцию, где на вход подаются значения аргумента, а на выходах получаются значения функции. Примером "черного ящика"-функции может служить телевизор: поворачивая ручку звука по часовой стрелке, мы всегда получаем усиление звука.
Если же мы будем крутить ручку швейной машины, то шов может получиться разный — все зависит от того, как настроена машинка (предполагается, что сами настроить машинку мы не можем), т.е. результат зависит от внутреннего состояния "черного ящика". Ящик этого типа называют автоматом. Таким образом, автоматом является тот "черный ящик", для которого результат работы зависит от его внутреннего состояния.

Рис. 7
Можно представить себе два крайних варианта "черных ящиков": "черный ящик" без входов {рис. 7) и "черный ящик" без выходов (рис. 8).
Примером "черного ящика" без входов может служить микропередатчик, который посылает сигналы о своем местонахождении, или генератор случайных чисел.

Р
ис.8Примером "черного ящика" без выходов может служить абсолютно черное тело, которое не отражает никакого света.
Можно представить себе такой "черный ящик", в котором выходы замыкаются на его входы, т.е. осуществляется так называемая обратная связь (рис. 9). Системы с обратной связью называют саморегулирующимися системами.
Понятие обратной связи возникло при разработке автоматических регуляторов. Одним из первых таких регуляторов был всем известный регулятор Уатта, управляющий подачей пара в цилиндры паровой машины.

Рис. 9
Примером саморегулирующихся систем может служить в принципе любой живой организм. При изменении температуры окружающей среды за счет саморегуляции температура тела человека практически остается постоянной. Также практически постоянной остается численность популяции каких-либо животных благодаря саморегулирующимся механизмам природы.
Конечно, равновесие саморегулирующихся систем может быть нарушено воздействием каких-либо факторов на систему. Если в популяции каких-либо животных человек истребит почти всех особей, то численность популяции может не восстановиться и эти животные могут исчезнуть совсем.
Наука о саморегулирующихся системах называется синергетикой.
Вопросы и упражнения
1. Что такое "черный ящик"?
2. Почему иногда бывает удобно рассматривать систему как "черный ящик" ?
3. В чем отличие "черного ящика"-функции и "черного ящика"-автомата?
4. Приведите примеры "черных ящиков" без входов и "черных ящиков" без выходов.
5. Приведите примеры саморегулирующихся систем в живой и неживой природе.
6. С помощью каких механизмов происходит саморегуляция температуры человека?
7. С помощью каких механизмов происходит саморегуляция численности популяции зайцев?
Понятие управления
Любой процесс в природе — физический, химический, социальный, мыслительный и т.п., будучи предоставлен сам себе, развивается и протекает по некоторым присущим ему закономерностям. Однако в силу всеобщей связи между явлениями в природе на него воздействуют и он сам воздействует на другие процессы. В результате таких воздействий происходят различные отклонения от первоначального развития процесса, т.е. он протекает по более сложным законам.
Все внешние воздействия на процесс можно разделить на случайные и управляющие. Случайные воздействия непреднамеренны (высокий снежный покров зимой затрудняет зайцам добычу пищи). Поведение влияющего процесса (выпадение снега) не зависит от состояния того процесса, на который он влияет (популяция зайцев), этот процесс протекает сам по себе, независимо от влияющего. Его, условно говоря, не интересует, что происходит под его влиянием. В противоположность этому управляющие воздействия специально предназначены для изменения хода процесса, на который они направлены (воздействие человека на численность популяции зайцев). Управляющие воздействия осуществляются с определенным намерением изменить ход процесса в желаемом направлении.
Совокупность управляющих воздействий, направленных на достижение поставленной цели, называется управлением. Таким образом, управление предполагает, что существует некоторый орган, вырабатывающий управляющие воздействия (в нашем примере это человек). Такой управляющий орган принято называть системой управления. Объект управления, на изменение состояния которого направлены управляющие воздействия, называют управляемой системой.
Чтобы цель управления была достигнута, в систему управления должна поступать информация о состоянии управляемой системы. Информация о состоянии управляемой системы позволяет скорректировать управляющие воздействия.
Схема управления изображена на рис. 10.
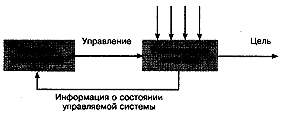
Рис. 10
Управляемые системы разнообразны по своему составу. Это могут быть определенные технические системы, живые организмы, коллективы людей, а также смешанные человеко-технические системы. Сущность управления системами одна. Она состоит в преднамеренном воздействии со стороны ради достижения заранее поставленных целей. Естественно, что способы управления техническими системами и системами, в которых действуют люди, принципиально различаются между собой. Однако сущность управляемой системы не зависит от качественного состава ее элементов.
Любая система в процессе своего функционирования претерпевает качественные изменения. Поэтому развиваемость является отличительным признаком систем. В механизме развития любой системы выделяют следующие стадии: возникновения, становления, зрелости и качественного преобразования (отмирания прежней системы). Причем последняя стадия, по существу, совпадает с первой, т.е. с возникновением новой системы или ее нового качества.
Растение (например, томат) возникает из семян, затем оно растет, развивается, дает плоды с новыми семенами и погибает. Здание, как система, сначала проектируется, затем строится, эксплуатируется и разрушается, что порождает необходимость построения нового здания.
Возникновение системы отождествляется с этапом проектирования системы. Готовый к применению проект можно считать рождением системы. Начало ее реализации, когда происходит отладка ее отдельных звеньев, согласование между субъектами правил пользования системой и т.д. совпадают с этапом становления системы. Реализация системы, когда происходит безболезненное разрешение противоречий между достигаемыми целями и складывающимися ситуациями, совпадает с этапом зрелости системы. Возникающие сбои при применении системы являются предпосылками для замены системы на новую, которая бы соответствовала изменившимся условиям. Это совпадает с этапом отмирания системы и. целесообразностью зарождения новой.
В соответствии с этапами развития системы задачи управления можно разбить на три группы.
1. Задачи конструирования новых систем.
2. Задачи совершенствования (улучшения) свойств систем и их функциональных возможностей.
3. Задачи использования (применения, эксплуатации, реализации) систем.
На основе указанных трех задач управления системами может быть рассмотрена комплексная задача управления, которая состоит в поэтапном конструировании, применении и в улучшении системы.
Вопросы и упражнения
1. Чем отличаются случайные и преднамеренные воздействия на процесс?
2. Приведите примеры случайных и преднамеренных воздействий.
3. Что такое управление? В чем состоит его сущность?
4. Что такое система управления ?
5. Что такое управляемая система?
6.
Приведите примеры систем управления и
управляемых систем.
7. Перечислите стадии развития любой системы и дайте характеристику каждой из них.
8. Приведите примеры развития систем различной природы.
Информация и управление
В 1948 году американский ученый Норберт Винер (1894—1964) "сформулировал основные положения новой науки, названной им "кибернетикой"". Он ввел в рассмотрение новую категорию — "управление". Выделение категории управления дало возможность пользоваться понятием информации, положив в основу кибернетики изучение законов передачи и преобразования информации.
Для функционирования системы необходим информационный обмен между элементами. Представьте себе бригаду рабочих, занятых на строительстве дома. Если каждый рабочий будет работать сам по себе, не получая информации о том, что делают остальные члены бригады, то вряд ли они смогут построить дом.
Без информационного обмена системы с окружающей средой также немыслимы функционирование и развитие системы, ее адаптация к постоянно меняющимся условиям и возможность воздействия на внешний мир, она не будет жизнеспособной. Если ребенок не будет получать информацию об окружающем мире или не будет взаимодействовать с ним, то из него не вырастет полноценного человека.
Таким образом, информационные связи необходимы, чтобы шли процессы управления как внутри самой системы, так и между системой и окружающей ее средой.
Для принятия решений по управлению системой нужна информация о состоянии управляемой системы и внешней среды.
Главным понятием системного подхода к сложным системам управления является понятие информационного потока. Система управления по своему определению требует взаимосвязи между частями для образования сложного интегрированного целого. Информационный поток должен обеспечить необходимой информацией все подсистемы.
Информационные потоки на схемах принято изображать полыми стрелками. Напомним, что описательная модель отвечает на вопрос "что мы хотим делать?", а алгоритмическая модель — на вопрос "как мы будем это делать?".
Разберем движение информационных потоков на примере создания и деятельности некоего завода.
Прежде чем строить завод, мы должны иметь какую-то начальную информацию, получаемую из внешних источников, в частности, информацию о цели построения завода и имеющихся ресурсах. Затем мы должны построить описательную модель, т.е. описать, каким мы хотим видеть наш завод. После этого надо построить алгоритмическую модель — разработать последовательность наших действий для достижения поставленной нами цели.
И только после этого можно приступать к реализации наших замыслов — начинать строить завод. В ходе построения завода необходимо постоянно собирать информацию о результатах деятельности. Полученную информацию каждый раз необходимо проанализировать, определиться с необходимостью внесения изменений в нашу систему, для того чтобы добиться своей цели. Возможно, нам придется внести изменения в описательную или алгоритмические модели, а возможно, в производственный процесс. Другими словами, мы должны принять решение, что нам необходимо сделать для скорейшего и более полного достижения цели.
На рис. 11 представлена схема движения информационных потоков.
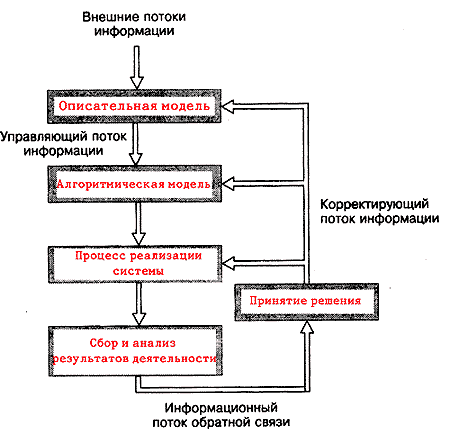
Рис. 11. Схема движения информационных потоков
Вопросы и упражнения
1. Какую роль играет информация в процессе управления ?
2. Расскажите о движении информационных потоков на каком-либо примере.
3. Объясните, почему корректирующий поток информации идет и к описательной, и к алгоритмической моделям, и к процессу реализации системы?
Цели системы
Система всегда создается для решения какой-либо задачи, для достижения какой-либо цели. Например, система водоснабжения города создается для бесперебойного снабжения города водой, правоохранительная система создается для охраны правопорядка, системы счисления созданы для удобства записи чисел.
Под целью системы понимают то состояние системы, которое надо достичь, или результаты, которые надо получить. Другими словами, цель определяет, для чего создается система.
Важность определения цели системы не вызывает сомнения и является, в свою очередь, сложной проблемой. Неправильное или недостаточно точное определение цели системы может привести к тому, что система не даст ожидаемых результатов. Например, в 30-е годы была выдвинута идея коллективизации сельского хозяйства. Ожидалось, что коллективизация приведет к улучшению положения в сельском хозяйстве, однако она привела его к развалу.
Как же правильно определить цель системы? Предположим, что вы поставили перед собой цель получить за год оценку "отлично" по математике.
Разумно поставить перед собой вопрос: "Зачем мне нужна отличная оценка по математике?" Предположим, вы ответили на этот вопрос так: "Я хочу поступить в политехнический университет". Это будет являться целью более высокого уровня.
Можно рассуждать так: "Я хочу сдать вступительные экзамены и поступить в политехнический университет. Что мне для этого надо?" Отвечая на этот вопрос, мы увидим, что на самом деле нам надо иметь хорошие знания по предметам, по которым придется сдавать вступительные экзамены, в том числе и по математике. Получается, что цель свою мы сформулировали несколько неправильно. Оказывается, что наша цель — получение отличных знаний, а не оценки!
Изменение цели может повлечь и изменение наших последующих действий. Отличную оценку можно получить, пользуясь шпаргалками. Но знаний от шпаргалок вряд ли прибавится!
Таким образом, чтобы правильно определить цели системы, надо сначала определить цели надсистемы, причем неплохо определить цели даже не на один, а на несколько уровней выше. В нашем примере надо задать себе вопрос: "Зачем мне поступать в политехнический университет?", а может, и вопрос: "Зачем мне нужно высшее образование?".
После формулировки цели надсистемы необходимо проверить, способствует ли достижение цели системы достижению цели надсистемы. Если вы получили отрицательный ответ, то вам следует пересмотреть свои цели.
Обычно, чем выше уровень системы, тем труднее бывает сформулировать цель и тем важнее сформулировать эту цель правильно.
Цели систем и надсистем удобно оформлять в виде "дерева". На рис. 12 приведен пример "дерева" для целей системы и надсистем. Здесь была поставлена цель:
"Знать математику". После этого поставлен вопрос: "Для чего мне надо знать математику?" — и получен ответ:
"Чтобы сдать вступительные экзамены в вуз". Затем, в свою очередь, задан вопрос: "Для чего мне сдавать экзамены?" — и получен ответ: "Чтобы поступить в вуз". Таким образом, мы как бы идем от нижних уровней "дерева" к верхним, к "корню дерева".
После того как мы поднялись на несколько уровней выше, надо двигаться, наоборот, сверху вниз и задавать себе вопрос: "Что для этого мне надо сделать?". Так, мы должны задать себе вопрос: "Что мне надо сделать, чтобы поступить в вуз?" Ответ: "Для этого мне надо получить аттестат об окончании школы, подать документы в вуз и хорошо сдать вступительные экзамены". Кроме того, надо проверить полноту своего ответа на этот вопрос. Для этого спросим себя: "Если я получу аттестат об окончании школы, подам документы в вуз и хорошо сдам вступительные экзамены, то я поступлю в вуз?" Если на этот вопрос мы получим отрицательный ответ, то это будет означать, что на вопрос: "Что мне надо сделать, чтобы поступить в вуз?" — был дан неполный ответ.
Аналогичным образом надо поступить с вопросом:
"Что мне надо сделать, чтобы хорошо сдать вступительные экзамены?"
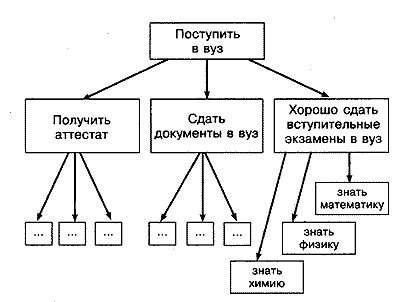
Рис. 12. "Дерево" целей надсистемы
Необходимо также провести анализ состояния системы, определить, в каком состоянии находится система на данный момент времени (исходное состояние системы) и в какое состояние мы хотим ее привести (желаемое состояние системы). Для этого нам надо определить критерии оценки состояния системы, по которым мы сможем оценить, в каком состоянии находится система, движемся ли к цели. Таким образом, чтобы правильно определить цели системы, необходимо:
1. Определить цели надсистемы, желательно на несколько уровней выше.
2. Определить, что надо сделать, чтобы добиться целей надсистем.
3. Проверить, добьемся ли мы целей надсистем, если будут достигнуты цели систем более низкого уровня.
4. Проанализировать исходное состояние системы, описать желаемое состояние системы и критерии оценки ее эффективности. Более подробно о критериях оценки эффективности системы мы поговорим дальше.
Вопросы и упражнения
1. Что понимают под целью системы?
2. Почему так важно правильно определить цели системы?
3. Приведите примеры, когда неправильное или неточное определение целей системы привело к тому, что система не дала ожидаемых результатов.
4. Как правильно определить цели системы ? Что для этого надо сделать?
Критерии оценки эффективности системы
Для правильного выбора характера и интенсивности управляющих воздействий необходимо знать, как указывалось выше, цель системы — желаемое ее состояние, а также критерии, по которым оцениваются степень и эффективность ее достижения.
Часто бывает очень трудно определить критерии. Как, например, определить, улучшилась ли культура обслуживания в парикмахерской, эффективно ли работает школа?
Определение цели может быть количественным или качественным. Качественные цели обычно носят психологический или социальный характер. К таким целям, например, относятся "поддержание чести фабричной марки", "улучшение взаимоотношений между сотрудниками", "повышение культуры обслуживания" и т.д.
Для качественных целей обычно бывает очень трудно подобрать критерии оценки достижения цели в единицах измерения, но это сделать необходимо. Общей единицей измерения часто бывает удобно принять деньги или время. В наиболее трудных случаях прибегают к экспертным оценкам, вводят с помощью экспертов условные перерасчетные коэффициенты одних единиц измерения в другие.
Цель системы должна быть сформулирована так, чтобы можно было определить критерии оценки достижения цели, т.е. цель системы и критерии оценки должны вырабатываться одновременно. Ставя какую-либо цель, необходимо каждый раз задаваться вопросом: как мы определим, достигли мы желаемой цели или нет?
Критерий оценки состояния системы, вообще говоря, может быть и один, но чаще их бывает несколько. Например, если мы налаживаем работу аэропорта, то критерием оценки будет не только количество перевозимых пассажиров, но и количество аварий, количество пустующих мест в самолетах, нарушения расписания и т.д.
Состояние системы в каждый момент времени определяется некоторым набором значений критериев. Состояние системы удобно изобразить с помощью пространства состояний. Для этого каждому параметру ставят в соответствие ось некоторого многомерного пространства. Любое состояние системы отображается в пространстве состояний некоторой точкой. Если состояние системы изменилось, то соответствующая точка в пространстве состояний должна переместиться.
Предположим, вы хотите получить как можно больше знаний и при этом не испортить себе здоровье, а по возможности и улучшить его. Тогда надо выбрать единицы измерения для знаний и для здоровья. Например, знания вы будете измерять в баллах — это будет средняя оценка, полученная в школе. Подобрать единицы измерения для здоровья несколько труднее. Можно, например, подсчитать количество дней, когда мы были здоровы, но поскольку время течет, то удобнее будет измерять в процентном отношении "здоровых" дней к количеству всех дней.
Тогда пространство состояний будет выглядеть так, как показано на рис. 13.

Рис. 13. Пространство состояний
Вопросы и упражнения
1. Для чего необходимо рассматривать критерии состояния системы?
2. В чем разница между количественными и качественными целями?
3. Приведите примеры количественных и качественных целей.
4. Что такое пространство состояний системы?
5. По каким критериям вы стали бы оценивать состояния следующих систем: парикмахерской, больницы, токарного станка, города, страны, телевизора, человеческого организма?
Оптимальное управление
Особенность задач управления состоит в том, что они допускают не одно, а несколько решений. Поэтому возникают вопросы: какое решение выбрать из всех возможных, какое из них будет наилучшим (оптимальным)?
При этом возникает новый вопрос: а какое же управление считать оптимальным?
Представим, что мы идем из школы домой. Какой путь будем считать наилучшим, если домой можно прийти несколькими путями? Если мы хотим прийти домой поскорее — это будет наикратчайший путь. Если мы хотим немного прогуляться, то наверняка выберем другой путь. Если же мы хотим зайти по дороге домой в магазин, то это может быть третий путь. Поэтому, если мы говорим об оптимальном решении, то надо говорить о критерии или критериях, по которым мы будем оценивать оптимальность решения, т.е. о критериях оптимальности. Критерий оптимальности называют также целевой функцией.
В сложных системах эффективность процесса обычно зависит от нескольких переменных, причем часть их надо обратить в максимум, а другие в минимум. Например, при создании газовой горелки мы хотим, чтобы расход топлива был минимальным, а температура пламени наибольшей.
Возникает вопрос: существует ли такое решение, которое удовлетворяет всем требованиям сразу? Вообще говоря, такого решения не существует. Если же оно и существует, то только в простейшем, тривиальном случае, когда в силу очевидности не возникает никаких проблем с выбором решения.
В реальных задачах обычно учитывают, что некоторые критерии имеют большую важность, чем другие. Поэтому приходится критерии ранжировать, т.е. устанавливать их относительную важность. В таких условиях оптимальным можно считать такое решение, в котором наиболее существенные критерии получают экстремальное значение, а остальные критерии не выходят из области допустимых значений.
Вспомните, например, как мы оценивали эффективность работы авиакомпании. Критериями оценки у нас были количество перевозимых пассажиров, количество несчастных случаев, количество пустующих мест в самолетах, нарушения расписания. Если надо добиваться увеличения числа перевозимых пассажиров, то остальные критерии надо постараться уменьшить. Причем наиважнейшим критерием надо, очевидно, выбрать количество несчастных случаев, ну а для остальных критериев можно подобрать области допустимых значений, из которых мы не должны выходить. Понятно, что количество пустующих мест в самолетах не должно превышать какого-то определенного числа, иначе авиакомпания просто разорится.
Вопросы и упражнения
1. Приведите примеры, когда задачи управления допускают не одно, а несколько решений.
2. Что понимают под оптимальным управлением?
3. Почему, когда мы говорим об оптимальном решении, нам приходится говорить о критериях оптимальности?
4. Приведите примеры задач управления, когда одни критерии необходимо обращать в максимум, а другие — в минимум.
5. Как выбрать оптимальное решение в условиях многокритериальной системы? Приведите примеры, когда критерии необходимо ранжировать.
Декомпозиция целей системы
Слово декомпозиция трактуется как разложение целого на части, предполагающее дальнейшее соединение этих составных частей в единое целое, т.е. в исходный объект.
Представление исходной цели совокупностью упрощенных (локальных) целей называют декомпозицией исходной цели, причем при достижении упрощенных целей должна быть достигнута и исходная цель. В свою очередь, эти упрощенные цели могут быть разбиты на более мелкие цели и задачи, т.е. можно говорить о многоуровневости целей и задач.
Например, цель "Получить высшее образование" может быть разбита на несколько более мелких целей:
"Поступить в институт", "Проучиться в институте положенное количество лет", "Защитить диплом".
В свою очередь, эти упрощенные цели могут быть разбиты на более мелкие цели и задачи, т.е. можно говорить о многоуровневости целей и задач. Цель "Поступить в институт" может быть разбита на: "Получить аттестат", "Сдать документы в институт", "Хорошо сдать вступительные, экзамены в вуз" (см. рис. 12).
Совокупность целей подсистем одного уровня должна обеспечить выполнение целей системы более высокого уровня. Поэтому при проведении декомпозиции цели необходимо каждый раз проверять, будет ли достигнута цель, если мы добьемся выполнения всех целей, на которые она разбита. То есть мы должны спросить себя;
"Гарантировано ли мое поступление в данный вуз, если я получу аттестат, сдам документы в институт и хорошо сдам вступительные экзамены в вуз?" Если мы ответили на этот вопрос отрицательно, значит, нам надо более четко сформулировать наши частные цели, либо мы потеряли одну или несколько частных целей.
В сложных системах достаточно высокого уровня не всегда удается однозначно определить одну-единственную цель. Возникает необходимость одновременного достижения нескольких целей, совокупность которых можно рассматривать как некоторую общую цель системы. Если эти цели независимы и равнозначны, имеем многоцелевую систему. Управление многоцелевыми системами представляет собой сложнейшую задачу.
Если среди совокупности целей одна доминирует по своему назначению над другими, ее называют основной, а остальные — дополнительными. Например, одновременно с выпуском основной продукции предприятие строит жилые дома и детские учреждения для своих сотрудников, сдает лом черных и цветных металлов, участвует в благоустройстве города и района и т.д. Естественно, для каждой из таких функций намечается своя цель, которая входит составной частью в общую цель, установленную для предприятия.
Чтобы добиваться от управляемой системы наилучшей работы, необходимо правильно оценить относительную значимость каждой из дополнительных или частных целей. Для определения важности целей можно присвоить каждой из них так называемый весовой коэффициент. Весовой коэффициент показывает относительную важность данной цели в долях единицы. Если q(i) — весовой коэффициент i-той цели, то q(1) + q(2) + q(3) + ... + q(k) = 1, где k. — количество целей.
Выразить важность цели числовым коэффициентом обычно трудно, эта величина, как правило, не поддается расчету, и для ее определения чаще всего приглашаются эксперты.
Вопросы и упражнения
1. Что такое декомпозиция целей? Для чего она нужна?
2. Что понимают под многоцелевой системой?
3. Приведите примеры многоцелевых систем. Есть ли в приведенных примерах основная и дополнительные цели? Если есть, то назовите их.
4. Что такое весовой коэффициент дополнительных или частных целей? Что он показывает?
Исследование операций
В середине нашего столетия стали формироваться отдельные научные направления, так или иначе связанные с понятием систем. Предметом одной из этих наук было обоснование методов принятия решений в военном деле. Она называется исследованием операций. В годы мировой войны для того, чтобы облегчить принятие решений, стали использовать результаты исследований, основанных на математических расчетах. Расчеты показывали возможные итоги различных военных операций. Эти методы, получившие общее название — исследование операций, и легли в основу новой науки.
Операцией называют комплекс мероприятий, направленных на достижение поставленной цели.
В дальнейшем стало ясно, что операции имеют место не только в военном деле. Операции характерны и для таких областей, как организация промышленности, транспорта, сельского хозяйства, обслуживания населения и т.д.
Поскольку природа реальных объектов и явлений, для которых необходимо строить математические описания, очень разнообразна, то существует несколько типов математических моделей.
Математическую модель исследования операций можно записать в виде функции W = F(x, у), где W — критерий качества функционирования системы (количественный), х — контролируемая переменная (или несколько переменных), т.е. переменная, которой мы можем управлять по своему усмотрению, у — неконтролируемая переменная (или несколько переменных), т.е. переменная, которой мы не можем управлять.
Переменная х принадлежит некоторому множеству Х допустимых значений контролируемых переменных, у принадлежит некоторому множеству Y возможных неконтролируемых факторов, влияющих на систему.
Переменные х обычно называют стратегией, а. функцию W называют целевой функцией.
Как мы уже отмечали, критерий качества может быть один, а может их быть и несколько. Задачи с одной целевой функцией (с одним критерием качества) называются задачами математического программирования. Более подробно с ними мы познакомимся дальше.
Модели исследования операций разбивают на три группы.
1. Детерминированная модель. Детерминированной моделью называют такую модель, в которой неконтролируемые факторы отсутствуют. В такой модели каждому из набора значений контролируемых переменных соответствует единственный результат. Детерминированная модель сопоставима с "черным ящиком" — функцией, где при одинаковых воздействиях на "черный ящик" мы всегда получаем одинаковый результат.
Для детерминированной модели наша цель — выбрать такую стратегию, для которой показатель качества W будет наивысший.
К детерминированным моделям относятся, в частности, модели, получающиеся при решении задач математического программирования.
2. Вероятностная модель. В жизни на реальные процессы влияют многочисленные неконтролируемые факторы. Довольно часто бывает известно, какие значения этих факторов появляются и с какой вероятностью (например, известно, как часто выходят из строя транзисторы в магнитофоне в зависимости от времени службы). Следовательно, при одной и той же стратегии мы можем получить различные результаты. Величина на выходе такой модели может быть представлена только в виде математического ожидания, т.е. мы можем предсказать, с какой вероятностью мы можем ожидать тот или иной результат.
Как же, в таком случае, выбрать наилучшую стратегию? В этом случае оценивают средние результаты.
Пусть у нас N вероятностных факторов у1 , у2 , ..., уn , которые появляются, соответственно, с вероятностью р1 , р2 , ..., рn . Тогда будем добиваться максимального значения для целевой функции W = рi F(x, уi).
Вероятностные модели получатся при моделировании, например, работы каких-либо технических устройств, когда известна вероятность выхода из строя их деталей, или при моделировании систем массового обслуживания (билетных касс, парикмахерских, телефонных станций и т.д.), где возникают очереди.
3. Неопределенная модель. В этом случае вероятность появления неконтролируемых факторов неизвестна, но обычно известно множество У — множество всех возможных неконтролируемых факторов. К таким факторам можно отнести погодные условия, действия конкурента или противника.
В неопределенной модели мы можем оценить только границы, в пределах которых мы можем получить результат. Так как множество Y известно, то выберем самый плохой результат, который только может быть: А = min(F(x, у)), — и самый лучший результат: В = max(F(x, у)). Тогда можно гарантировать, что результат нашей операции будет не хуже, чем А, и не лучше, чем В. Таким образом, в условиях неопределенности мы не можем получить точного решения. Но тем не менее такое решение будет лучше, чем взятое наугад.
Методами обоснований решений в условиях неопределенности занимаются математическая теория игр и теория статистических решений. В теории игр рассматриваются ситуации, когда имеются несколько участников выполнения операций, каждый из которых преследует различные и противоположные цели, т.е. при наличии противника. Такие случаи характерны для военных действий, но также часто встречаются в области экономики при наличии конкуренции. Кроме того, они встречаются в спорте и в самых разнообразных играх в буквальном смысле этого слова.
Вопросы и упражнения
1. Что называется операцией?
2. Запишите математическую модель исследования операций и поясните ее.
3. Что называется стратегией?
4. Что такое целевая функция?
5. Что такое детерминированная модель? Приведите примеры.
6. Что такое вероятностная модель? Приведите примеры.
7. Что такое неопределенная модель? Приведите примеры.
8. Приведите примеры задач, когда возникает модель того или иного типа.
Задачи математического программирования
Напомним, что задачи с одной целевой функцией (с одним критерием качества) называются задачами математического программирования. Математическое программирование изучает методы нахождения экстремумов функций многих переменных при наличии ограничений на эти переменные.
Заметим, что термин "программирование" здесь не связан с составлением программ для ЭВМ.
Рассмотрим несколько задач такого типа.
Задача о дневном рационе
Пусть дневной рацион гусей на ферме составляется из трех продуктов — П1 , П2 , П3 . Необходимое количество этих продуктов обозначим, соответственно, х1 , х2 , х3 , а их стоимость — с1 , с2, с3 . Тогда стоимость всего рациона будет выражаться функцией
F(х1,х2,х3)=cх1+ cх2+ сх3.
Но для нормального развития гусей рацион должен содержать определенное количество питательных веществ, а именно: не менее b1 единиц белков, b2 — жиров, b3 — углеводов, b4 — витаминов. Известно, что в единице продукта П1 содержится а11 единиц белка, а12 единиц жиров, а13 единиц углеводов и а14 единиц витаминов. Аналогично, в продукте П2 содержится а21, a22, a23, a24, а в продукте П3 - а21, a22, a23, a24, соответствующих питательных веществ.
Все эти величины удобно свести в таблицу (см. табл. 2).
Величины х1 , х2, х3 неизвестны, их надо выбрать, остальные же величины заданы. Причем величины х1 , х2 , х3 следует выбрать так, чтобы стоимость рациона была наименьшей, но при этом в рационе содержалось необходимое количество питательных веществ, т.е. должны выполняться неравенства:
a11x1 + a12x2 + a13x3 >= b1
a2x1 + a22x2 + a23x3 >= b2
a31x1 + a32x2 + a33x3 >= b3
a41x1 + a42x2 + a43x3 >= b4
x1 >= 0; x2>=0; x3>=0
Таблица 2
|
Питательные вещества |
Количество питательных веществ в единице продукта |
Минимально необходимое количество питательных веществ |
||
|
П1 |
П2 |
П3 |
||
|
Белки |
a11 | a12 | a13 | b1 |
|
Жиры |
a21 | a22 | a23 | b2 |
|
Углеводы |
a31 | a32 | a33 | b3 |
|
Витамины |
a41 | a42 | a43 | b4 |
|
Стоимость единицы продукта |
c1 | c2 | c3 | |
|
Количество единиц продукта |
x1 | x2 | x3 | |
Задача о выпуске продукции
Пусть некий завод выпускает три вида продукции: П1,. П2 , П3.
Для выпуска этой продукции требуется четыре вида ресурсов (например, электроэнергия) и три вида сырья. Запасы ресурсов ограничены. Расход ресурсов на единицу продукции и другие величины указаны в табл. 3.
Таблица 3
|
Виды ресурсов |
Расход ресурсов на единицу продукции |
Запасы ресурсов |
||
|
П1 |
П2 |
П3 |
||
|
Электроэнергия |
a11 | a12 | a13 | b1 |
|
Ресурс 1 |
a21 | a22 | a23 | b2 |
|
Ресурс 2 |
a31 | a32 | a33 | b3 |
|
Ресурс 3 |
a41 | a42 | a43 | b4 |
|
Стоимость единицы продукта |
c1 | c2 | c3 | |
|
Количество единиц продукта |
x1 | x2 | x3 | |
Нам необходимо спланировать производство (т.е. выбрать х1 , х2 , х3) так, чтобы доход был максимальный. Доход выражается функцией f.
f(x1,x2,x3)=c1x1 + с2x2 + с3x3.
Поскольку запас ресурсов ограничен, то должны выполняться неравенства:
11x1 + a12x2 + a13x3 <= b1
a2x1 + a22x2 + a23x3 <= b2
a31x1 + a32x2 + a33x3 <= b3
a41x1 + a42x2 + a43x3 <= b4
x1 >= 0; x2>=0; x3>=0
Задача об эвакуации
Пусть некий завод производит эвакуацию. На заводе имеется п предметов, подлежащих эвакуации. Но в распоряжении завода есть всего один самолет, который может загрузить не более А тонн груза. Известны вес каждого предмета (a1 , а2 , ..., аn ) и его стоимость (с1 , с2 , ..., сn ). Задача состоит в том, чтобы вывести предметов на возможно большую сумму.
Введем п переменных х1 , х2 , ..., хn . Эти переменные могут принимать одно из двух значений: 0 — если данный предмет загружается в самолет, и 1 — если не загружается.
Тогда нам надо найти набор значений переменных х1 , х2 , ..., хn , удовлетворяющих условиям:
хj= 0 или хj= 1 для всех j = 1, 2, ..., п;
а1х1 + a2x2, + ... + аnхn < А,
при котором функция
f(х1, х2, ....xn) = с1x1 + с2x2 + ... + сnхn
принимает максимальное значение.
Мы видим, что при всем кажущемся различии приведенных здесь задач их математическая форма очень сходна.
В первых двух задачах ограничения имеют вид линейных неравенств. Задачи такого типа называют задачами линейного программирования. Отметим, что в задачах линейного программирования ограничения могут быть выражены не только неравенствами (строгими или нестрогими), но и равенствами.
Третья задача относится к задачам нелинейного программирования, поскольку на переменные накладывается условие целостности.
Прикладные задачи математического программирования обычно содержат большое количество переменных, поэтому их решение без помощи ЭВМ весьма затруднительно.
Вопросы и упражнения
1. Задачи какого типа относятся к задачам математического программирования ?
2. Что изучает математическое программирование?
3. Задачи какого типа относятся к задачам линейного программирования?
4. Почему задачи математического программирования решаются обычно с помощью ЭВМ?
Имитационное моделирование
Имитационное моделирование — это искусственный эксперимент, при котором вместо проведения натурных испытаний с реальными объектами проводят опыты с помощью математических моделей.
Имитационное моделирование обычно связано с моделированием динамических (изменяющихся во времени) объектов, процессов и явлений. Например, на железной дороге существуют табло, на которых отражается движение вагонов и поездов на сортировочной станции. Здесь диспетчер имеет дело с отображающей моделью, т.е. моделью, отражающей действительное положение дел. Аналогичные табло используются и в учебных центрах, где обучают будущих диспетчеров. Но в этом случае обучающимся предлагаются какие-либо вымышленные ситуации, которые лишь имитируют реальность. В этом случае речь идет об имитационном моделировании.
Для иллюстрации этого метода рассмотрим ставшую "классической" задачу "о сбежавшем крокодиле".
Предположим, что в некотором городе есть зоопарк, из которого ровно в полночь сбежал крокодил. Крокодил не знал, куда ему идти, и поэтому, дойдя до очередного перекрестка, выбирал направление случайным образом. Для простоты будем считать, что крокодил за один час проходил ровно один квартал. Поскольку дело происходило ночью, то искать крокодила начали только через пять часов после побега. Крокодил же через пять часов блужданий испугался появившихся на улицах города машин и где-то спрятался. Спрашивается:
как далеко успел убежать крокодил и в каком квартале его надо искать в первую очередь?
Конечно, можно провести натурный эксперимент:
выпустить из зоопарка порядка 30 крокодилов и посмотреть, куда они пойдут... Нелепость такого опыта очевидна, поэтому лучше провести искусственный эксперимент.
Поскольку крокодил выбирает направление своего движения случайно, то провести эксперимент мы можем с использованием генератора случайных чисел. Генератор случайных чисел должен вырабатывать одно из четырех определенных чисел. Пусть это будут числа 1, 2, 3 и 4. Если генератор случайных чисел выдаст число 1, то будем считать, что наш крокодил пошел на восток, 2 — на запад, 3 — на юг, 4 — на север.
Теперь можно проводить искусственный эксперимент, рисуя движение крокодила, например, на бумаге. Но еще удобнее провести этот эксперимент на компьютере, составив необходимую для этого программу.
Таким образом, мы с вами получим вероятностную модель.
Вопросы и упражнения
1. Что такое имитационное моделирование?
2. Когда возникает необходимость в имитационном моделировании ?
3. Составьте программу на известном вам языке программирования для проведения искусственного эксперимента со сбежавшим крокодилом на компьютере и проведите его.
Этапы системного анализа
Подведем итоги. Системология, или системный анализ, является прикладной наукой. Он направлен на решение "жизненных", плохо поставленных задач.
Укрупненно системный анализ состоит из этапов постановки задач, структуризации системы, построения и исследования модели.
1-й этап.
Постановка задачи. На этом этапе нужно выяснить, что мы хотели от управляемой системы — для чего она создана, как функционирует, в каких терминах может быть сформулирована ее цель и в чем она состоит, как оценивается эффективность ее работы, какие существуют ограничения. Выяснение ответов на эти вопросы практически не поддается формализации. Успех определяется искусством и опытом специалистов по системному анализу, глубиной понимания исследуемой системы, умением установить контакты с работающими в системе специалистами.
В то же время этот начальный этап имеет определяющее значение, от него зависит успех всей последующей работы.
2-й этап.
Структуризация системы. Этот этап начинается с локализации системы, установления ее границ. Для этого определяют полный набор элементов, в той или иной степени связанных с поставленной задачей, и делят их на два класса — входящих в исследуемую систему и ее внешнюю среду. Определение элементов системы и ее внешней среды существенно зависит от постановки задачи.
Структуризация рассматриваемой системы заключается в разбиении ее на подсистемы в соответствии с поставленной задачей. Вообще говоря, делить систему на подсистемы можно по любому признаку, но важно найти такую структуру, которая обеспечивает наилучшую эффективность решения задачи. Нельзя забывать при этом, что совокупность функций, выполняемых подсистемами, обеспечивает выполнение функций системы в целом. При необходимости каждая подсистема может быть тоже структурирована.
Во внешней среде локализуют системы, которым исследуемая система или подчинена, или находится с ними во взаимодействии. Определяются приоритеты этих систем по принципу близости связей с исследуемой.
Завершается этап структуризации определением всех существенных связей между исследуемой системой и системами, выделенными во внешней среде.
3-й этап.
Построение модели. Мы создаем для себя некоторое представление об изучаемом объекте или процессе, помогающее лучше понять его функционирование и устройство, его характеристики, т.е. создаем модель. Модели значительно облегчают понимание системы, позволяют проводить исследования в абстрактном плане, прогнозировать поведение реальной системы в интересующих нас условиях. Основное назначение и преимущество модели заключается в том, что в ней сконцентрированы важные факторы реальной системы, которые подлежат изучению в конкретном исследовании. Несущественные факторы либо отсутствуют в модели, либо отражены в ней в небольшой степени.
Наиболее важное преимущество модели — возможность простыми средствами изменять ее параметры; вводить некоторые воздействия с целью изучения реакции системы. В реальных условиях получить аналогичные сведения значительно труднее и дороже, а иногда и просто невозможно (например, изучение работы системы в аварийных условиях).
Чтобы модель можно было хорошо изучить и проводить с нею эксперименты, она сама должна быть достаточно простой. Однако чем проще модель, тем в меньшей степени она соответствует моделируемому процессу или объекту. Поэтому моделирование всегда компромисс между простотой модели и обеспечиваемой ею точностью.
При моделировании сложных систем используют различные виды моделей. Наиболее мощным средством исследования, анализа и синтеза систем являются математические модели.
4-й этап
Исследование модели. Этот этап проводится после того, как модель получена и проверена на соответствие реальной системе. Основным назначением этогс этапа является выяснение поведения моделируемой системы в различных условиях, при разных состояниях самой системы и ее внешней среды. Для этого варьируют параметры модели, характеризующие состояния объекта, и задают на ее входах различные значения параметров. Полученные результаты позволяют выяснять поведение реальной системы в соответствующих условиях и определить, какие следует ввести изменения в модель, а затем и в реальную систему для улучшения ее функционирования.
Вопросы и упражнения
1. Перечислите этапы системного анализа.
2. Охарактеризуйте каждый из этапов системного анализа.
Список литературы
1. Абчук Б.А. 1 : 7 в нашу пользу (Азбука решений). М.: Радио и связь, 1982.
2. Абчук В.А., Емельянов А.А., Матвейчук Ф.А. Введение в теорию выработки решений. М.: Воениздат, 'L972.
3. Вершинин О.Е. За страницами учебника информатики. М.: Просвещение, 1992.
4. Теин А. Г. Земля Информатика. Екатеринбург: Издательство Уральского университета. Издательство Дома учителя, 1997.
5. Информатика. Энциклопедический словарь для начинающих. М.: Педагогика-Пресс, 1994.
6. Кофман А., Фор Р. Займемся исследованием операции. М.: Мир, 1966.
7. Мамиконов А.Г. Принятие решений и информация. М.: Наука, 1983.
8. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. М.: Высшая школа, 1989