13.1. Общие вопросы
В файле alloc.h находятся прототипы функций для работы с динамической памятью. В частности, имеется возможность динамического создания и уничтожения объектов. Проще говоря, нужна переменная — создадим ее, выделим под нее память, не нужна — уничтожим, освободим занимаемую данной переменной память (эту память потом снова можно использовать). Эти действия производятся в специально выделенной области памяти, которую и называют динамической (иногда динамическую память еще называют "кучей" — heap). Функций для работы с динамической памятью, вообще говоря, довольно много, но мы станем использовать всего две — malloc и free. Посредством malloc в куче выделяется память под объект (столько, сколько мы запросим), посредством free — память, занятая объектом, освобождается и может быть вновь использована. Эти функции являются аналогом процедур new и dispose в Паскале.
Функция malloc имеет следующий прототип:
void *malloc(size_t size) ;
Единственным параметром функции malloc (тип size_t — просто беззнаковый целый) является количество байт, требуемое для размещения объекта в динамической памяти. Обычно (см. примеры ниже) это количество указывается не явно, а посредством операции sizeof. Так, для выделения памяти под данное типа int можно, конечно, написать malloc(2) , но значительно более мобильными будут программы, в которых используется конструкция вида malloc(sizeof(int)). Функция malloc возвращает указатель на выделенную область памяти или NULL, если выделить память не удалось (например, вся свободная память в куче исчерпана). Поскольку тип возвращаемого указателя void, его можно привести к указателю на любой другой тип (это особенность указателей на тип void). Приведем пример использования функции malloc:
int. *p;
p=(int *)malloc(sizeof(int) );
Функция free, которая используется для освобождения памяти в куче, имеет следующий прототип:
void free(void *block) ;
Ей передается указатель на объект, который мы "уничтожаем" (освобождаем занимаемую им память). Вопрос "откуда free знает, сколько именно байтов памяти надо освободить" лежит за рамками нашего краткого курса (для ответа на него требуется рассмотреть "внутреннюю кухню" процессов, происходящих в динамической памяти).
13.2. Однонаправленные списки
Посредством объектов, распределяемых в динамической памяти, можно организовывать различные динамические структуры данных, такие, как списки (однонаправленные и двунаправленные) и двоичные деревья. Мы ограничимся лишь самыми простыми примерами, поскольку содержательные вопросы использования динамических структур к используемому языку программирования отношения не имеют. Начнем, как это обычно и делают, с однонаправленных списков.
Не давая формального определения однонаправленного списка, поясним лишь, что он представляет собой структуру данных, каждый элемент которой имеет ссылку (указатель) на следующий элемент. Последний элемент в поле ссылки содержит NULL. Для работы с однонаправленным списком необходимо иметь указатель на его голову (первый элемент), ведь двигаться по такому списку можно лишь в одном направлении.
В приведенной ниже программе продемонстрированы некоторые типичные учебные задачи на однонаправленные списки. Необходимые пояснения даны в комментариях.
#include <stdio.h>
#include <alloc.h>
/* Структура для описания односвязного (однонаправленного)
списка*/
typedef int ELEMTYPE;
typedef struct node { ELEMTYPE elem; struct node * next;} *LIST;
/* Инициализация списка/ как пустого */
LIST init(LIST *l)
{ return *l=NULL;}
/* Добавление элемента в голову списка */
LIST cons (ELEMTYPE e,LIST l)
{ LIST news=(LIST)malloc(sizeof(struct node));
news->elem=e;
news->next=l;
return news;
}
/* Печать списка целых */
void printlist(LIST l)
{ printf("\n") ;
while (l!=NULL) (printf("%5d",l->elem);l=l->next;;}
}
/* Добавление элемента в конец списка */
LIST last(ELEMTYPE e,LIST l)
{ LIST head;
if (!l) { l=(LIST)malloc(sizeof(struct node)) ;
l->elem=e;
l->next=NULL;
return l;
}
else { head=l;
while (l->nexti=NULL) l=l->next;
l->next= (LIST) malloc (sizeof (struct
node) ) ;
l=l->next;
l->elem=e;
l->next=NULL;
return head;
}
}
/* Удвоить все вхождения данного элемента в список */
LIST doubleE(ELEMTYPE E,LIST l)
{ LIST head=l,tmp;
while (l)
if (l->elem==E)
{/* вставить после него */
tmp=l->next;
l->next=(LIST)malloc(sizeof(struct node))
;
l->next->elem=l->elem;
l->next->next=tmp;
l=tmp;
}
else l=l->next;
return head;
}
/* Удалить из списка все вхождения
заданного элемента */
LIST delE(ELEMTYPE E,LIST l)
{ LIST head=l,w;
if (!l) return head;
while (l->next)
if (l->next->elem==E) {w=l->next;l->next=l->next->next;
free(w);}
else l=l->next;
return head;
}
/* Тестирующая программа */
void main(void)
{
LIST p;
init(&p) ;
p=last(0,p); p=cons(l,p); p==cons (2, p) ; p=cons(3,p); p=last(4,p);
p=last(5,p); p=last(6,p); p=cons(2,p); p=last(4,p);
printlist(p);
p=doubleE(2,p) ;
printlist(p) ;
p=doubieE(4,p) ;
printlist(p) ;
p=delE(4/p) ;
printlist (p) ;
}
13.2.1. Использование стека (реализованного в виде однонаправленного списка) при работе с выражениями, записанными в "польской" форме записи
Рассмотрим пример использования однонаправленного списка для организации стека в алгоритмах перевода арифметического выражения в "польскую" (префиксную) форму записи и вычисления значения выражения, записанного в такой форме. Начнем с вычисления выражения — соответствующий алгоритм записывается совсем просто. Чтобы не уделять слишком много внимания техническим деталям, будем считать, что выражение, записанное в префиксной форме записи, содержит только цифры и знаки четырех бинарных арифметических операций. Вот примеры таких выражений: +12, +—123, *+12+34, ~*+12+345 — и т.д.
В приведенной ниже программе реализован следующий алгоритм.
Просматриваем выражение, записанное в префиксной форме записи, с конца, Если встречается число (в нашем случае — цифра), бросаем его в стек. Если встречается знак операции, вынимаем из стека два верхних числа, производим над ними данную операцию и результат снова бросаем в стек. То, что останется в стеке, когда выражение закончится, и есть результат (следует обратить внимание, что первым извлекается из стека второй операнд, т.е. для операций вычитания и деления — вычитаемое и делитель соответственно),
#include <stdio.h>
#include <alloc.h>
#include <dos.h>
/* Описание стека - однонаправленного списка.
В этой программе
ничто не мешает сделать стек глобальным */
struct node {float data;struct node *next;} *stack;
/* Поместить элемент в стек */
void push (float x)
{ struct node *w=(struct node*)malloc(sizeof(struct node)) ;
w->data=x;
w->next=stack;
stack=w;
}
/* Снять значение со стека и вернуть его */
float pop(void)
{ float ret=stack->data;
struct node *w=stack;
stack=stack->next;
free (w) ;
return ret;
}
/* Функция вычисления выражения в
префиксной форме записи */
float value(char *s)
{ float x,y;
char *start=s;
while (*s) s++;s--;
for (;s>=start;s--)
if ((*s)>='0'&&(*s)<='9') push(*s-'0');
else switch (*s)
{ case '+':x=pop();y=pop();push(x+y);break;
case '-':x=pop();y=pop();push(y-x);break;
case '*':x=pop();y=pop();push(x*y);break;
case '/':x=pop();y=pop();push(y/x) ;
}
return pop() ;
}
void main(void)
{ stack==NULL;
if (_argc<2) printf("\nНет параметра в
командной строке");
else printf("\n%f",value(_argv[1]));
}
Теперь приведем программу перевода выражения, записанного в инфиксной форме записи, в префиксную форму записи. Как и в предыдущем примере, будем считать, что выражение состоит из цифр, но теперь, помимо знаков четырех арифметических операций, оно может содержать скобки.
Для перевода выражения из инфиксной в префиксную форму записи оно просматривается с конца. В отличие от предыдущей программы в стеке хранятся не числа, а знаки операций, причем они не просто там хранятся, но и взаимодействуют между собой. В частности, операции с меньшим приоритетом ("+" и "—") "выбрасывают" из стека расположенные ниже операции с большим приоритетом "*" и "/", если они не "защищены" скобкой ")". При появлении парной скобки "(" из стека "в порядке общей очереди" выбрасываются все расположенные между скобками знаки операций (сами скобки при этом "уничтожаются").
#include <stdio.h>
#include <alloc.h>
#include <dos.h>
#include <string.h>
/* Описание стека - однонаправленного
списка. В этой программе
ничто не мешает сделать стек глобальным */
struct node {char data;struct node *next;} *stack;
/* Поместить элемент в стек */
void push(char x)
{ struct node *w=(struct node*)rnalloc (sizeof (struct node)) ;
w->data=x;
w->next=stack;
stack=w;
}
/* Снять значение со стека и вернуть его */
char pop(void)
{ float ret=stack->data;
struct node *w=stack;
stack=stack->next;
free(w) ;
return ret;
}
/* "Подсмотреть" значение на вершине
стека */
char pick(void)
{ return stack->data;}
/* Функция вычисления выражения в
префиксной форме записи */
char * infix2prefix(char *s) {
char *tempres=(char*)malloc(strlen(s)+1),*res;
int i=0,j;
char *start=s;
while (*s) s++;s--;
for (;s>=start;s--)
if ( (*s)>='0'&&(*s)<='9')
tempres[i++]=*s;
else switch (*s)
{ case '*':case '/':push (*s) ,break;
case '+':case'-': while (pick()=='*'|| pick ()=='/')
tempres[i++]=pop();
push(*s);break;
case ')':push(*s); break;
case '(':while (pick()!=')') tempres[i++]=pop();pop();
}
res=(char *)malloc(i);
i--;j=0;
while (i>=0) res[j++]=tempres[i--] ;
res[j]=0;
return res;
}
void main(void)
{ char *s=(char *)malloc(strlen(_argv[1])+3) ;
/* "Навесим" на строку лишние внешние
скобки - так проще ее обрабатывать */
strcpy(s+l,_argv[l]);
s[0]=' (' ;strcat(s,") ") ;
stack=NULL;
if (_argc<2) printf("\nНет параметра в
командной строке");
else printf("\n%s",infix2prefix(s)) ;
}
13.2.2. Красивые (но, увы, крайне неэффективные) решения списочных задач
"Ноги" приведенных ниже решений списочных задач растут из языка Лисп. Мы иногда показываем ребятам, что задачи на списки можно решать и таким способом, хотя, разумеется, эти решения не могут быть использованы в реальных производственных задачах (но их можно и модифицировать для повышения эффективности).
Определим структуру для однонаправленного списка и четыре функции (car, cdr, cons, null), которые назовем "примитивами". Названия функций совпадают с "лисповскими" первоисточниками (для удобства чтения мы повторим ряд небольших фрагментов, которые использовались в приведенных выше программах):
typedef int elemtype;
struct node { elemtype elem;
struct node *next;
};
typedef struct node *List;
elemtype car(list k)
{ return l->elem;}
elemtype cdr(list 1)
{ return l->next;}
list cons(elemtype e,list l)
{ list tmp=(list)malioc(sizeof(struct node)) ;
tmp->next=l;
tmp->elem=e;
return tmp;
}
int null(list l)
{ return (l==NULL);}
Продемонстрируем, как посредством данных примитивов можно решать различные списочные задачи. Пусть, к примеру, нам надо найти последний элемент непустого списка. Как мы будем это делать? Разумеется, дойдем до конца списка (т.е. найдем такой элемент, у которого ссылка на следующий равна NULL), и вот он — последний элемент. Это совсем простое итеративное решение, в нем описывается, как найти последний элемент. Но посмотрим на задачу с другой стороны: а что такое последний элемент непустого списка? Если список состоит из одного элемента, то это — его первый элемент ("голова"). А если в списке больше одного элемента, то последний элемент списка — это последний элемент его "хвоста". Запишем это:
int last (list l)
{ if (null(cdr(l))) return car(l);
else return last(cdr (l));
}
Теперь попробуем получить "начало" непустого списка (часть списка без последнего элемента). Итеративное решение этой задачи очевидно, но рекурсивное записывается еще проще! Что такое "начало" списка? Если список состоит из одного элемента, то его начало пусто. В противном случае начало списка есть первый элемент ("голова"), добавленный к началу "хвоста". Это мы и запишем:
list begin(list l}
{ if (null(cdr(l))) return NULL;
else return cons(car(l),begin(cdr(l)));
}
Пока мы решили две совсем простые задачки, которые и итеративно решаются "на счет раз". А вот более сложная: пусть требуется получить список, перевернутый по отношению к данному (учтите, список однонаправленный). Попробуйте решить эту задачу итеративно, а потом (только потом!) взгляните на рекурсивное решение:
list reverse(list l)
{ if (null(l)) return NULL;
else return cons(last(l),reverse(begin (l)));
}
Функции с переменным числом параметров
Мы до сих пор не касались вопроса о том, чем некоторые "стандартные" функции Си отличаются от тех, которые пишем мы. Показательный пример — функция printf. Она обладает замечательным свойством — может иметь переменное число параметров. Мы таких функций писать пока не умеем (и, кстати, в Паскале средств для написания собственных функций и процедур с переменным числом параметров нет, подобные функции и процедуры бывают только стандартными). В Си функции с переменным числом параметров реализуются совсем просто. Приведем сначала пример, а потом кратко поясним, как он работает (фактически в этом примере показано, как работает функция printf). Итак, пример:
#include <stdio.h>
#include <stdarg.h>
#include <string.h>
void param(char *s,...)
{
int i,n=strlen (s);
va_list ap;
va_start(ap,n);
printf("\n") ;
while (*s)
switch (*s++)
{ case ' d ' :printf ("%d ",va_arg(ap,int));break;
case 'f ':printf("%f ",va_arg(ap,double));
}
va_end(ap);
}
void main(void)
{ param("ddffd",10,12,1.5,0.1,15);}
Функция param имеет переменное число параметров, первый из которых — строка, в которой записаны буквы "d" и " f", указывающие на тип каждого параметра из списка. Для работы со списком параметров требуется подключить заголовочный файл stdarg.h, в котором находятся прототипы трех функций (на самом деле это макросы, но для нас этот вопрос не является существенным) — va_start, va_arg и va_end. Тип va_list также определен в этом файле, он используется для описания указателя на очередной параметр. Посредством va_start этот указатель инициализируется (при этом требуется указать число параметров), с помощью va_arg очередной параметр извлекается из списка (при этом надо указать его тип). Вызовом va_end работа со списком параметров завершается.
Замечание. Вы, вероятно, обратили внимание, что вещественное число в функцию передается не как float, а как double. Это особенность Си.
Теперь мы можем привести функцию makelist, которая формирует список из своих аргументов (их количество является вторым параметром). Обратите внимание, что элементы списка записываются при вызове функции makelist в обратном порядке (сразу после количества элементов записывается последний элемент списка).
list makelist(list l,int n,...)
{ int i;
va_list ap;
va_start(ap,n) ;
for ( i=1;i<=n;i++) l=cons(va_arg(ap,elemtype),l);
return l;
}
Приведем еще несколько примеров рекурсивных решений списочных задач:
/* Входит ли элемент в список?
*/
int member(elemtype
e,list l)
{ if (null(l)) return 0;
else if (e==car(l)) return 1;
else return
member(e,cdr(l));
)
/* Получить новый список, удалив из
исходного все вхождения данного элемента */
list remove(elemtype x,list l)
{ if (null(l)) return NULL;
else if (х==саr(l)) return remove(x,cdr(l));
else return cons(car(l),remove(X,cdr(l)));
}
/* Вставить элемент в упорядоченный список
*/
list insert(elemtype e,list 1)
{ if (null(l)). return makelist(NULL,1,e);
else if (e<car(l)) return cons(e,l);
else return cons(car(l),insert(e,cdr(l)));
}
/* Получить новый список объединением
данных */
list append(list l,list r)
{ if (null(l)) return r;
else return cons(car(l),append(cdr(l),r));
}
/* Слить два упорядоченных списка */
list merge(list 1,list r)
{ if (null(l)) return r;
else return insert(car(l),merge(cdr(l),r));
}
/* Отсортировать список */
list sort(list 1)
{ if (null(l)) return NULL;
else return insert(car(l),sort(cdr(l)));
}
/* Найти длину (количество элементов)
списка */
int. len(list l)
{ if (null(l)) return 0;
else return 1+len(cdr(l1)) ;
}
/* Найти количество вхождений данного
элемента в список */
int counte(elemtype e,list l)
{ if (null(l)) return 0;
else if (car(l)===e) return 1+counte (e, cdr
(l) ) ;
else return counte(e,cdr(l));
}
/* Удвоить все вхождения данного элемента в список */
list doublee(elemtype e,list l)
{ if (null(l)) return NULL;
else if (car(l)==e) return append(makelist(NULL,2,e,e),doublee(e,cdr(1)));
else return cons(car(1),doublee(e,cdr(l)));
}
13.3. Двунаправленные списки
Как и при рассмотрении однонаправленных списков, мы не станем давать формального определения двунаправленного списка, а ограничимся описанием данной структуры. Каждый элемент двунаправленного списка имеет как минимум два ссылочных поля. Одно служит для указания на элемент, предшествующий данному, другой указывает на следующий элемент списка. Обычно эти поля называются prev и next соответственно. У первого элемента списка поле prev==NULL, у последнего — next=-NULL. При работе с двунаправленным списком нет необходимости иметь указатель именно на первый элемент, ведь по такому списку можно "ходить" в двух направлениях.
При использовании двунаправленного списка мало что меняется по сравнению с однонаправленным — просто при каждой операции приходится "заботиться" еще об одном поле связи. Ниже приведена программа с теми же самыми функциями, что ранее были реализованы для однонаправленных списков, только применительно к двунаправленным спискам.
#include <stdio.h>
#include <alloc.h>
/* Структура для описания двусвязного (двунаправленного)
списка*/
typedef int ELEMTYPE;
typedef struct node2 { ELEMTYPE elem; struct node2 *prev, *next;} *LIST2;
/* Инициализация списка, как пустого */
LIST2
init(LIST2 *1)
{ return *1=NULL;}
/* Добавление элемента в голову списка */
LIST2 cons (ELEMTYPE e,LIST2 l)
{ LIST2 n=(LIST2)malloc(sizeof(struct node2));
n->elem=e;
n->next=l;
n->prev=NULL;
l->prev=n;
return n;
}
/* Печать списка целых */
void printlist(LIST2 1)
{ printf("\n");
while (1!=NULL) {printf("%5d",1->elem);1=l->next;;}
}
/* Добавление элемента в конец списка */
LIST2
last(ELEMTYPE e,LIST2 1)
{ LIST2 head;
if (!1) { l=(LIST2)malloc(sizeof(struct node2));
l->elem=e;
l->next=NULL;
l->prev=NULL;
return l;
}
else { head=l;
while (l->nextl=NULL) l==l->next;
l->next=(LIST2)malloc(sizeof(struct node2)) ;
l->next->prev=l;
l=l->next;
l->elem=e;
l->next=NULL;
return head;
}
}
/* Удвоить все вхождения данного элемента
в список */
LIST2 doubleE(ELEMTYPE E,LIST2 l)
{ LIST2 head=l,tmp;
while (l)
if (l->elem==E)
{/* вставить после него */
tmp=l->next;
l->next=(LIST2)malloc(sizeof(struct node2)) ;
l->next->elem=l->elem;
l->next->next=tmp;
l->next->prev=l;
l->tmp;
}
else l=l->next;
return head;
}
/* Удалить из списка все вхождения
заданного элемента */
LIST2 delE(ELEMTYPE Е,LIST2 1)
{ LIST2
head=l,w;
if (!l) return head;
while (l->next)
if (l->next->elem==E)
{ w=l->next;
l->nехt=l->nехt->nехt;
if (l->next!=NULL) l->next->prev=l;
free(w) ;
}
else l=l->next;
return head;
}
/* Тестирующая программа */
void main(void)
{
LIST2 p;
init(&p) ;
p=last(0,p); p=cons(1,p); p=cons(2,p); p=cons(3,p); p=last(4,p);
p=last(5,p); p=last(6,p); p=cons(2,p); p=last(4,p);
printlist(p);
p=doubleE(2,p) ;
printlist(p) ;
p=doubleE(4,p) ;
printlist(p) ;
p=delE(4,p) ;
printlist(p);
}
13.4. Двоичные деревья
В данном разделе приводятся примеры
функций для работы с двоичными деревьями (в
частности,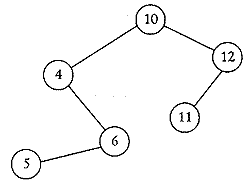
деревьями поиска). Напомним (это
не формальное определение), что двоичное
дерево называется деревом поиска, если для
любой вершины выполняется условие: все
элементы в ее левом поддереве меньше
элемента в данной вершине, а все элементы в
правом поддереве — больше. К сожалению, в
рамках нашего краткого курса нет
возможности подробно рассматривать сами
алгоритмы работы с деревьями поиска,
поэтому приведем только примеры
соответствующих функций, сопроводив их
комментариями. Для вывода двоичного дерева
мы используем два способа. Один (для вывода
в текстовом режиме) — "отступами" —
менее наглядный, другой (для вывода дерева в
графическом режиме) — "кругами" —
более 
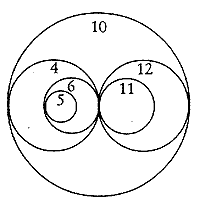наглядный (на наш взгляд). Поясним на
примере, что значит вывести дерево "кругами".
Пусть у нас имеется следующее двоичное дерево (см. рис. справа).
При выводе его "кругами" картинка будет иметь вид:
#define M 10
#define max(x,y) ( ( (х) > (у) ) ? (х) : (у) )
#include <stdio.h>
#include <alloc.h>
#include <string.h>
#include <stdlib.h>
#include <graphics.h>
#include <niath.h>
#inciude <conio.h>
/* Описание типов для представления двоичного дерева */
typedef int ELEMTYPE;
typedef struct node
{ELEMTYPE elem;
struct node *left;
struct node *right;
} *TREE;
/* Инициализация двоичного дерева */
TREE initT(TREE
*t)
{ return *t=NULL;}
/* Добавление элемента в двоичное дерево
поиска */
TREE addT(ELEMTYPE e,TREE t)
{
if (!t) ( t=(TREE)malloc(sizeof(struct node)) ;
t->elem=e;
t->left=t->right=NULL;
}
else
if (t->elem<e) t->right=addT(e,t->right) ;
else if (t->elem>e) t->left=addT(e,t->left);
return t;
}
/* Удаление элемента из двоичного дерева
поиска */
void del(TREE *r,TREE *t)
{ TREE q;
if ((*r)->right==NULL)
{
(*t)->elem=(*r)->elem;
q= ( + r ) ;
(*r) =(*:r)->left;
free(q) ;
}
else del(&<(*r)->right),t);
}
void delTtTREE *t,ELEMTYPE e)
{
if ( (*t)!=NULL)
if (e<(*t)->elem) delT(&((*t)->left),e) ;
else
if (e> (*t) ->elem) delT (& ( (*t)->right) , e) ;
else
if ((*t)->left==NULL) (*t)=(*t)->right;
else
if ((*t)->right==NULL) (*t)=(*t)->left;
else del(&((*t)->left),t) ;
}
/* Печать дерева "отступами" */
char * format (int width)
{ char * buf=(char*)malloc(10) ;
itoa(width,buf+1,10) ;
strcat(buf+1,"d") ;
buf[0]='%';
return buf;
}
void printT(TREE t,int h /* отступ */)
{char *f;
if (t) { printT(t->left,h+3);
printf ( "\n") ;
f=format (h) ;
printf(f,t->elem) ;
printT(t->right,h+3) ;
}
}
/* Функция вычисления глубины дерева */
int
downT(TREE t)
{ if (t==NULL) return 0;
else return max(1+downT(t->left),1+downT(t->right));
}
/* Количество элементов дерева */
int cardT(TREE t)
{
if (t—NULL) return 0;
else return 1+cardT(t->left)+cardT(t->right);
}
/* Вспомогательные графические функции
преобразования координат */
int xs (int x)
{return 320+x;}
int уs(int у)
{return 240-у;}
/* Функция рисует дерево "кругами" и
вписывает в круги значения*/
void drawT(TREE t,int A,int В,int у)
{ float e,xl,xr;
int sc,oldcolor;
char values[6] ;
int size;
if (t!=NULL)
{ circle(xs((A+B)/2),ys(y),abs <B-A)/2) ;
itoa(t->elem,values, 10) ;
size=3+cardT(t->left)+cardT(t->right) ;
settextstyle(SMALL_FONT,0,size) ;
outtextxy(xs((A+B)/2),ys(y+abs(B-A)/2),values) ;
if ((t->left!-NULL)&&(t->right!=NULL))
{ sc= (cardT(t->left)+cardT(t->right))
;
e=abs(B-A)/sc;
xl=(A+e*cardT(t->left)) ;
xr=(B-e*cardT(t->right)) ;
drawT(t->left,A,xl,y) ;
drawT(t->right,xr,B,y) ;
}
else if ((t->left—NULL)&&(t->right!=NULL)) drawT(t->right,(A+B)/2,B,y)
;
else if ( (t->left!=NULL)&&(t->right==NULL)) drawT(t->left,A,(A+B)/2,y);
}
}
void main(void)
{ TREE p;
int z,gd=DETECT,gm;
initT(&p) ;
do
{printf("\Введите элемент дерева:"};scant("%d",&z);
if (z) p=addT(z,p) ;
}
while (z!=0) ;
printT(p,10) ;
getch () ;
initgraph (&gd, &gm, "c : \\tc") ;
drawT(p,-220,220,0) ;
getch();
closegraph() ;
do
{ printf("\Введите элемент для удаления:");scanf("%d",&z);
del T (&p, z) ;
printT(p,10) ;
}
while (z!=0);