Имеются различные определения понятия "фрактал", однако уже почти четверть века назад один из ведущих специалистов в этой области, бельгийский математик Бенуа Мандельброт (его именем назван один из самых знаменитых фрактальных объектов — множество Мандельброта, алгоритм построения изображения которого мы также рассмотрим), отмечал, что ни одно из определений не представляется удовлетворительным, ибо всегда находятся объекты, которые, по-видимому, имеют фрактальную природу, но не удовлетворяют данному определению. Понятие фрактала в чем-то схоже с понятием компьютерного вируса. И в том, и в другом случае не существует (на данный момент) строгого определения понятия, но есть некоторое характерное свойство (также плохо формализуемое), которое присуще всем объектам, которые принято относить к данному классу. Для компьютерных вирусов таким свойством является способность к самовоспроизведению, для  фракталов — самоподобие. Именно на это свойство, как на характерное для всех известных фракталов различной природы, указывал и Б.Мандельброт.

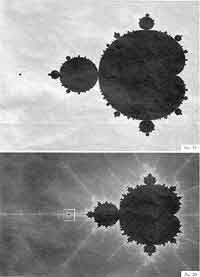
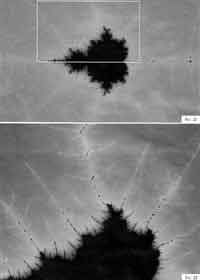
На. рис. 19—22 приведена последовательность "снимков" множества Мандельброта, полученных при  возрастающем увеличении. На них видно, что, "погружаясь" во множество Мандельброта, мы все время встречаем похожие друг на друга фрагменты.

Автором одного из самых изящных способов построения фрактальных кривых является ученый, чья основная специальность весьма далека от математики и программирования. Это биолог Аристид Линдермауер. Именно он предложил простой и изящный способ построения фрактальных объектов, напоминающих природные. Данный способ получил в честь его создателя название L-системы. Хотя посредством L-систем можно задавать разнообразные, в том числе и известные "чисто математические" объекты, такие, как замечательные кривые Гильберта, Пеано и пр., все же основное, что привлекает к ним внимание, — возможность строить изображения, удивительно напоминающие объекты, созданные природой, — деревья, кусты, травинки.

Замечание. Некоторые поклонники языка Лого в шутку утверждают, что первая буква в названии метода вовсе не от фамилии Линдермауер, а от названия их любимого языка. И хотя это, конечно, не так, мы скоро увидим, что у них больше оснований для этого утверждения, чем кажется на первый взгляд.

Рассмотрим исполнителя (черепашку), который имеет память, организованную в виде стека (т.е. он может вспомнить лишь то, что запомнил в последний раз), и умеет "ползать по плоскости" и выполнять несколько простых команд (см. ниже).

Текущее состояние черепашки описывается набором из трех параметров (х, у, a):

   х, у — текущие' координаты черепашки;
   a — угол, определяющий направление, в котором черепашка ползет по команде "вперед".

Начальное состояние черепашки описывается набором из пяти параметров: (х₀, y₀, a₀, step_move, step_a). Здесь х₀, y₀, a₀ — начальные значения координат и угла, а
step_move — шаг (шаг определяет длину одного шага черепашки, который она делает по команде "вперед");
step_a — угол поворота (угол поворота определяет, на сколько поворачивается черепашка, иными словами, на сколько меняется угол а при выполнении команд "налево" и "направо").

Черепашка умеет выполнять следующие команды (каждая команда кодируется одним символом):

"F" — переместиться вперед (на step_move), в направлении а, оставив след (отрезок);
"+" — повернуться направо (по часовой стрелке) на угол step_a (при исполнении этой команды меняется только угол а);
"—" — повернуться налево (против часовой стрелки) на угол step_a (при исполнении этой команды также меняется только угол а);
" [" — запомнить (отложить в стек) текущее состояние (х, у, a);
" ] " — вспомнить (взять из стека и установить) последнее запомненное состояние.

Программой для черепашки является строка, в которой, кроме указанных символов, могут встречаться и любые другие. Черепашка просматривает строку-программу символ за символом. Команды она выполняет, а символы, не являющиеся командами, пропускает.

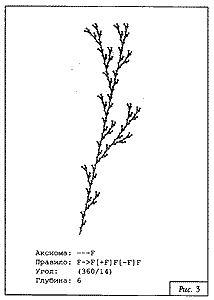
Рассмотрим два примера (мы будем приводить лишь строку-программу и угол поворота step_a, поскольку остальные параметры влияют на ориентацию и размер» но не на вид фрактальной кривой).

Строка-программа:

- - - -F [+] [-]F[-FFF] [+FFF]F[+F[+
][-]] [-F[+] [-]]F[-FFF] [+FFF]F[-F
FF] [+FFF]F[-FFF] [+FFF] F [+F [+]
[-]F[-FFF][+FFF]F[+F[+] [-] ] [-F
[l+] [-]]] [-F[+] [-]F[-FFF] [+FFF]
F[+F [+][-] ][-F [+][-]]]
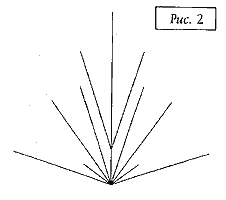Угол поворота: (360/14) градусов (мы привели его в таком виде, поскольку в программах используется не сам этот угол, а число, на которое делится 360, т.е. 14).

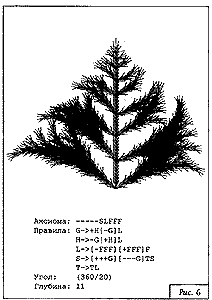
Строка-программа:

-----[++++-[+][-+[-]][-
FFF] [+FFF] F][---+-[+][-
 +[-]] [-FFF] [+FFF]F][-
FFF][+FFF]F[++++[-]][[-
--+[-]][+++][---][-
FFF] [+FFF] FFFF
Угол поворота: (360/20)

Разумеется, приведенные здесь строки-программы мы получали не "руками". Рассмотрим алгоритм получения этих строк, предложенный А.Линдермауером.

Пусть имеются некоторая строка, которую мы назовем аксиомой (ахioms), и набор строк, называемых правилами (rule₁, rule₂, ... rule_n). Аксиома может быть любой, а правила должны иметь вид символ —> строка. Приведем пример:

Аксиома: ----G
Правила: G->GFX [+G] [-G]
                 X->X[-FFF] [+FFF]FX

Сначала положим результирующую строку равной аксиоме. Станем просматривать ее слева направо. Если встречается символ, являющийся первым символом одного из правил, заменим его на строку из соответствующего правила.

Так, после первого шага из приведенной аксиомы и правил получается следующая строка: ----GFX [+G] [-G].

После второго шага: ----GFX[+G] [-G]FX[-FFF] [+FFF] FX [+GFX [+G] [-G] ] [-GFX[+G] [-G] ]

И, наконец, после третьего шага: -—GFX [+G] [-G]FX[-FFF] [+FFF]FX[+GFX[+G] [-G] ] [-GFX[+G] [-G]]FX[-FFF] [+FFF]FX[-FFF] [+FFF]FX[-FFF] [+FFF] FX [+GFX [+G] [-G]FX[-FF F] [+FFF] FX [+GFX [+G] [-G] ] [-GFX[+G] [-G] ] ] [-GFX[+G] [-G]FX[-FFF] [+FFF] FX [+GFX [+G] [-G] ] [-GFX[+G] [-G]]]

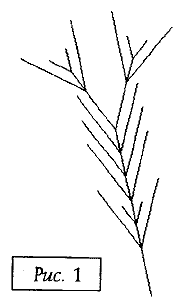
Если удалить из полученной строки все "незначащие" символы, то получится строка-программа, по которой был построен рис. 1.

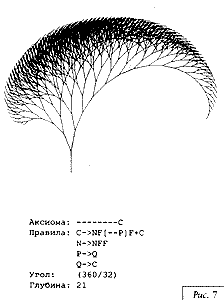
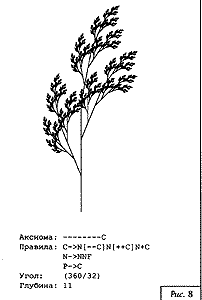
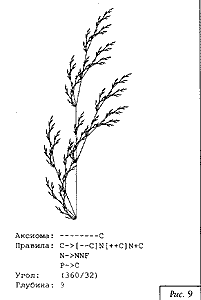
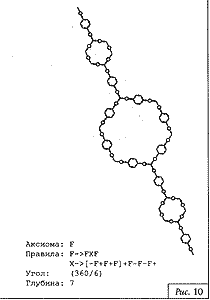
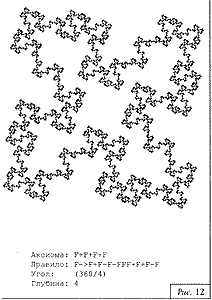
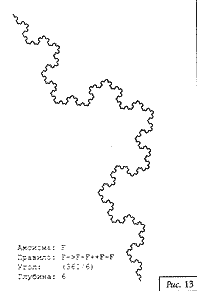
На рис. 3—15 приведены примеры двухмерных фрактальных L-кривых. Для каждой кривой указаны аксиома, правила, угол поворота и количество просмотров строки.

Программа построения двухмерных L-фракталов (язык Си). 

Программа построения двухмерных L-фракталов (язык QBasic) .

В предыдущем разделе мы рассмотрели способ построения двухмерных L-фракталов. Если научить черепашку "летать", можно получить очень красивые и реалистичные изображения пространственных (трехмерных) L-кривых. Рассмотрим, как это делается.

Во-первых, понятно, что изменения коснутся лишь собственно "черепашьей графики". Способ получения строки-программы по аксиоме и правилам никак не влияет на то, как эта программа выполняется черепашкой.

Во-вторых, легко видеть, что, выйдя в пространство, черепашка должна получить еще одну координату для описания ее состояния. Ну и наконец, направление движения черепашки тоже будет определяться не одним углом, а... тут возможны варианты. Можно определять направление двумя углами, можно — тремя координатами (на плоскости мы тоже могли вместо угла использовать две координаты конца вектора, задающего направление). Нам показалось удобным (и более наглядным) определять направление движения черепашки именно тремя координатами (хотя вам, быть может, больше понравится другой способ).

 Более формально направление движения черепашки будет определяться тремя координатами конца единичного вектора, начало которого закреплено в начале координат.

Кроме того, черепашка должна научиться менять направление своего движения в пространстве. Для этого вводятся шесть дополнительных команд:

"+" — поворот направо (по часовой стрелке) на угол step_a вокруг оси OZ;
"—" — поворот налево (против часовой стрелки) на угол step_a вокруг оси OZ;
"&" — поворот направо (по часовой стрелке) на угол step_a вокруг оси OY;
"^" — поворот налево (против часовой стрелки) на угол step_a вокруг оси OY;
">" — поворот направо (по часовой стрелке) на угол step_a вокруг оси ОХ;
"<" — поворот налево (против часовой стрелки) на угол step_a вокруг оси ОХ.

(Помимо данных, мы введем еще одну команду — "¦" — изменить направление движения на противоположное.)

Приведем формулы геометрических преобразований в пространстве, которые требуются для реализации трехмерной черепашьей графики.

Пусть состояние черепашки описывается следующим образом: (х_t, у_t,z_t, direct_x, direct_y, direct_z). Здесь (х_t, у_t,z_t,) — текущие координаты черепашки, а (direct_x, direct_y, direct_z) — текущие координаты вектора направления direct.

По команде "F" черепашка перемещается вперед на step_move в направлении вектора direct. Более формально:

        x_t = x_t + step_move·direct_x
        y_t = y_t + step_move·direct_y
        z_t = z_t + step_move·direct_z

По командам "+ " и "— " выполняется поворот вектора направления (на угол -step_a и step_a соответственно) вокруг оси OZ:

       direct_x = direct_x · cos(a) - direct_y · sin(a)
       direct_y = direct_x · sin(a) + direct_y · cos(a)
       direct_z = direct_z

По командам "&" и "^" выполняется поворот вектора направления (на угол —step_a и step_a соответственно) вокруг оси OY:

       direct_x = direct_x · cos(a) - direct_z · sin(a)
       direct_y = direct_y
       direct_z = direct_x · sin(a) + direct_z · cos(a)

И, наконец, по командам "<" и ">" выполняется поворот вектора направления (на угол -step_a и step_a соответственно) вокруг оси ОХ:

       direct_x = direct_x
       direct_y = direct_y · cos(a) - direct_z · sin(a)
       direct_z = direct_y · sin(a) + direct_z · cos(a) 

По команде "¦" координаты направляющего вектора direct меняются на противоположные:

       direct_x = - direct_x
       direct_y = - direct_y
       direct_z = - direct_z

Для того чтобы получить изображение трехмерной кривой, которую вычерчивает черепашка, необходимо спроектировать ее на плоскость. Мы используем перспективное проектирование.

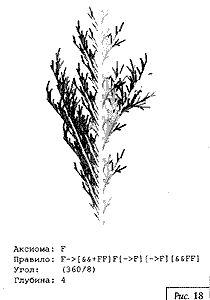
На рис. 16—18 приведены примеры трехмерных L-кривых (для них, как и для двухмерных, указаны аксиома, правила и угол поворота).

Программа построения трехмерных L-фракталов (язык Си).

В царстве морских коньков (множество Мандельброта)

Множество Мандельброта — один из самых известных фрактальных объектов — впервые было построено Бенуа Мандельбротом весной 1980 г. в исследовательском центре фирмы IBM им. Томаса Дж. Уотсона. И хотя исследования подобных объектов начались еще в прошлом веке, именно открытие этого множества и совершенствование аппаратных средств машинной графики в решающей степени повлияли на развитие фрактальной геометрии и теории хаоса. Итак, что же такое множество Мандельброта?

Для знакомства с множеством Мандельброта необходимо иметь представление о комплексных числах и операциях над ними. Отметим, что слова "иметь представление" полностью соответствуют действительности, соответствующие понятия легко объяснить в течение нескольких минут. Обычно мы решаем "фрактальные" задачки с детьми 10-х или 11-х классов, но вполне можно использовать их и раньше (например, в 8-м или 9-м классах). Далее приводится краткое математическое отступление.

Система координат на прямой вводится указанием начальной точки и единичного отрезка. Прямая с введенной на ней системой координат называется числовой потому, что каждому действительному числу на ней соответствует некоторая точка. Часто говорят также о "числовой плоскости" — плоскости с введенной на ней системой координат (например, декартовой). Но если с прямой все понятно, то почему плоскость числовая? Как установить соответствие между числами и точками на плоскости? Если речь идет о действительных числах, то — никак. Но можно ввести понятие комплексного числа, представляя комплексное число парой действительных (фактически парой координат соответствующей точки на плоскости). Комплексное число, соответствующее точке (x, у), записывают в виде х + yi, где i — так называемая комплексная единила — точка (0, 1). Для комплексных чисел вводится понятие действительной и мнимой части (это просто абсцисса и ордината соответствующей точки). Действительная и мнимая части комплексного числа z. обозначаются как Re z. и Im z соответственно.

Нам понадобится ряд простых понятий, связанных с комплексными числами. Во-первых, рассмотрим, как определяются операции сложения и умножения комплексных чисел.

Пусть z = z₁ + z₂,  тогда
Re z = Re z₁ + Re z₂,  Im z = Im z₁ + Im z₂

Пусть теперь z == z₁ • z₂, тогда
Re z = Re z₁ • Re z₁ — Im z₁ • Im z₂,
Im z  = Re z₁ • Im z₂ + Re z₂  • Im z₁
(из данного определения, в частности, видно, что комплексные числа +i и —i являются корнями квадратными из —1).

Кроме двух этих операций, мы станем использовать понятие модуля комплексного числа, который определяется следующим образом: Геометрически сумма комплексных чисел представляется суммой векторов, соответствующих этим числам, а модуль комплексного числа равен длине соответствующего вектора.

Рассмотрим функцию комплексного переменного f(z) = z² +c. Положим z₀= 0 и рассмотрим последовательность {z_n}, где . Такая последовательность может быть ограниченной (т.е. может существовать такое R, что либо "убегать в бесконечность" (т.е. ). Множество Мандельброта можно определить как множество комплексных чисел с, для которых указанная последовательность является ограниченной. К сожалению, не известно аналитического выражения, которое позволяло бы по данному с определить, принадлежит ли оно множеству Мандельброта или нет. Поэтому для построения множества используют компьютерный эксперимент: просматривают с некоторым шагом множество точек на комплексной плоскости, для каждой точки проводят определенное число итераций (находят определенное число членов последовательности) и смотрят за ее "поведением". Доказано, что множество Мандельброта размещается в круге радиуса 2 с центром в начале координат. Таким образом, если на некотором шаге модуль очередного члена последовательности превышает 2, можно сразу сделать вывод, что точка, соответствующая с, определяющему данную последовательность, не принадлежит множеству Мандельброта. Понятно, что даже если мы проделаем очень большое, но конечное число итераций (а только так мы и можем поступить), а точки так и останутся в круге радиуса 2, мы не сможем гарантировать, что с принадлежит множеству Мандельброта. Уменьшая шаг, с которым просматриваются комплексные числа, и увеличивая количество итераций, мы можем получать сколь угодно подробные, но всегда лишь приближенные изображения множества.

Но позвольте, скажете вы, а как же получаются все те красивые картинки, которые приводятся всегда, когда заходит речь о множестве Мандельброта? Ведь из приведенного объяснения видно, что изображения множества должны быть черно-белыми (например, мы можем отмечать черным цветом точки, принадлежащие множеству, и белым — не принадлежащие). Замечательные цветные изображения получаются на границах множества Мандельброта, если рассматривать не только вопрос "убегает точка в бесконечность или нет", но и скорость такого убегания. Опишем соответствующий процесс подробнее. Пусть в нашем распоряжении имеется N цветов, занумерованных для определенности от 0 до N— 1. Будем считать, опять же для определенности, что черный цвет имеет номер 0. Если для данного с после N—1 итерации точка не вышла за круг радиуса 2, будем считать, что с принадлежит множеству Мандельброта и покрасим эту точку с в черный цвет. Иначе, если на некотором шаге К (1 < К < N— 1) очередная точка вышла за круг радиуса 2 (т.е. на К-м шаге мы поняли, что она "убегает"), покрасим ее в цвет К. Красивые изображения получаются при удачном выборе окрестности множества (а именно вне множества мы и получим "цветные" точки) и подборе палитры. 

На рис. 23—35 представлены изображения множества Мандельброта и его фрагментов. Следует учесть, что  при верстке изображения были масштабированы и кадрированы.

Программа для построения множества Мандельброта (и  его фрагментов)

Видел бы это Жюлиа... (множества Жюлиа)

Удивительно, но множества Жюлиа, тесно связанные с множеством Мандельброта, были исследованы еще в начале XX века математиками Гастоном Жюлиа и Пьером Фату. В 1917—1919 гг. ими были получены основополагающие результаты, связанные с итерированием функций комплексного переменного. Вообще говоря, этот факт заслуживает отдельного обсуждения и является впечатляющим примером математического исследования, на многие десятилетия опередившего время (ученые могли лишь приблизительно представлять, как выглядят исследуемые ими объекты!), но мы, ограниченные рамками одной газетной публикации, опишем лишь способ построения множеств Жюлиа для функции комплексного переменного f(z)= z² +c.

Говоря более точно, мы будем строить так называемые "заполняющие множества Жюлиа". Рассмотрим прямоугольник (x₁, у₁) — (x₂,y₂). Зафиксируем константу с и станем просматривать точки выбранного прямоугольника с некоторым шагом. Для каждой точки, как и при построении множества Мандельброта, проведем серию итераций (чем больше число итераций, тем точнее будет получено множество). Если после серии итераций точка не "убежала" за границу круга радиуса 2, поставим ее черным цветом, иначе — белым.

На рис. 36— 39 представлены изображения множеств Жюлиа.

Программа для построения множеств Жюлиа .