Сортировка и поиск
(Конспекты занятий)
С.М.Окулов
1. Алгоритмы сортировки
Для решения многих задач необходимо
упорядочить данные по определенному признаку. Этот процесс называют
сортировкой. Для простоты изложения мы будем рассматривать одномерный массив из
целых чисел:
Const NMax=... ;
Type MyArray=Array[l..NMax] Of Integer;
Var A:MyArray;
Суть большинства алгоритмов сортировки от такого
упрощения не изменяется. Алгоритмы сортировки отличаются друг от друга степенью
эффективности, под которой понимается количество сравнений и количество
обменов, произведенных в процессе сортировки. В основном мы будем оценивать
эффективность количеством операций сравнения (порядком этого значения).
Заметим, что элементы массива можно сортировать:
• по возрастанию — каждый следующий элемент больше предыдущего —
А [1] < А [2] < ... < A[N];
• по неубыванию — каждый
следующий элемент не меньше предыдущего А[1] <= А [2] <= ... <=
A[N];
• по убыванию — каждый
следующий элемент меньше предыдущего А[1] > А [2] > ... > A[N];
• по невозрастанию — каждый следующий элемент не больше
предыдущего А [1] >= А [2] >= ... >= A [N].
Научившись выполнять одну сортировку, изменить ее, чтобы получить
другую, не составляет особого труда.
Рассмотрим некоторые из алгоритмов сортировки так, как они излагались и
изучались на занятиях по этой теме.
Сортировка
простым выбором
Рассмотрим идею данного метода на
примере. Пусть исходный массив состоит из 10 элементов:
5 13 7 9 1 8 16 4 10 2
После сортировки массив должен выглядеть так:
1 2 4 5 7 8 9 10 13 16
Процесс сортировки представлен ниже. Максимальный элемент текущей части
массива заключен в кружок, а элемент, с которым происходит обмен, — в
квадратик. Скобкой помечена рассматриваемая часть массива, т.е. еще не
упорядоченная.
1-й шаг. Рассмотрим весь массив и найдем в нем максимальный
элемент — 16 (стоит на седьмом месте), поменяем его местами с последним
элементом — с числом 2.
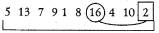
Максимальный элемент помещен на свое
место.
2-й шаг. Рассмотрим часть
массива — с первого до девятого элемента. Максимальный элемент этой части — 13,
стоящий на втором месте. Поменяем его местами с последним элементом
неупорядоченной части — с числом 10.
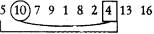
Отсортированная часть массива состоит теперь уже
из двух элементов.
3-й
шаг. Уменьшим рассматриваемую часть массива на один элемент. Здесь нужно
поменять местами второй элемент (его значение — 10) и последний элемент этой
части — число 4.
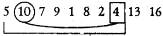
В отсортированной части массива — 3 элемента.
4-й шаг.
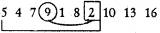
5-й
шаг. Максимальный элемент этой части
массива является последним в ней, поэтому его нужно оставить
на месте.

6-й
шаг.

7-й шаг.
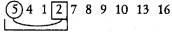
8-й шаг.
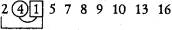
9-й шаг.
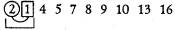
Фрагмент программной реализации.
Procedure Sort;
Var i, j, k: Integer;
m:Integer; {Значение максимального
элемента рассматриваемой части массива.}
Begin
For i:=N DownTo 2 Go Begin
{Цикл по длине рассматриваемой
части массива.}
{Поиск максимального элемента и
его номера в текущей части массива.}
k: =i; m: =А [ i ] ;
{Начальные значения максимального
элемента и его индекса в рассматриваемой части массива.}
For j:=l To i-1 Do If
A[j]>m Then
Begin :k:=j; m:=A[k] End;
If k<>i Then
{Перестановка элементов.)
Begin A[k] :=A[i],;A[i]
:=m;End;
End;
End;
Оценим
количество сравнений. При первом просмотре N — 1, при втором — N — 2, при
последнем — 1. Общее количество С =
N — 1+N — 2 + ...+ 1= N• (N- l)/2, или C=O(N2).
Методические рекомендации. Выше
приведен материал на 10— 15 минут занятия. В качестве заданий для самостоятельной
работы можно предложить:
1.
Модифицировать алгоритм так, чтобы осуществлялась сортировка:
•
четных элементов массива;
•
элементов, записанных на нечетных местах;
• отрицательных элементов массива и т.д.
2. Пусть N является точным квадратом
натурального числа, например, 3. Разделим массив на 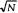 групп по
групп по 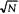 элементов в каждой. Выберем максимальный
элемент в каждой группе... Лучше рассмотреть пример попроще.
элементов в каждой. Выберем максимальный
элемент в каждой группе... Лучше рассмотреть пример попроще.
Дан массив
7 10 3 5 15 9 6 12 8.
При
разбивке на группы - (7 10 3) (5 15 9) (6 12 8). Максимальные элементы 10 15
12. Максимальный из них 15, он во второй группе. Если оставшиеся элементы из
второй группы, а это 5 и 9, меньше 10 и 12, то мы нашли сразу три элемента,
записываемые на свои места. Если нет, то заменяем максимальные элементы
элементами из группы. Этот метод был предложен Э.Х. Фрэндом в 1956 году и
получил название метода квадратичного выбора. Количество сравнений имеет
порядок O(N• 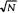 ). Метод
интересен с точки зрения проверки техники программирования.
). Метод
интересен с точки зрения проверки техники программирования.
Сортировка простым обменом
Рассмотрим идею метода на примере. Отсортируем по возрастанию массив из
5 элементов: 5 1 8 4 9. Длина текущей (неупорядоченной) части массива — (N — k
+ 1), где k — номер просмотра, i — номер первого элемента
проверяемой пары, номер последней пары — N — k.
Первый
просмотр: рассматривается весь
массив.
i= 1 5 4 8 2 9
> меняем
i= 2 4 5 8 2 9
< не меняем
i= 3 4 5 8 2 9
> меняем
i =
4 4 5 2 8 9
< не меняем
9 находится на своем месте.
Второй просмотр: рассматриваем
часть массива с первого до предпоследнего элемента.
i= 1 4 5 2 8 9
< не меняем
i=2 4 5 2 8 9
> меняем
i= 3 4 2 5 8 9
< не меняем
8 — на своем месте.
Третий просмотр:
рассматриваемая часть массива содержит три первых элемента.
i= 1 4 2 5 8 9
> меняем
i= 2 2 4 5 8 9
< не меняем
5 — на своем месте.
Четвертый просмотр:
рассматриваем последнюю пару элементов.
i= 1 2 4 5 8 9
< не меняем
4 — на своем месте.
Наименьший элемент — 2 оказывается на
первом месте. Количество просмотров элементов массива равно N-1.
Этот
метод также называют методом "пузырька". Название это происходит от
образной интерпретации, при которой в процессе выполнения сортировки более
"легкие" элементы (элементы с заданным свойством) мало-помалу
всплывают на "поверхность".
Приведем процедуру "пузырьковой" сортировки.
Procedure Sort;
Var k, i, t:Integer;{k — номер
просмотра, изменяется от 1 до N-1;
i — номер первого
элемента рассматриваемой пары;
t — рабочая переменная для перестановки местами
элементов массива.}
Begin
For k:=l To N-1 Do
{Цикл по номеру просмотра.}
For i:=l To N-k Do
If 'A[i]>A[i+l] Then
{Перестановка элементов.} Begin
t:=A[i];A[i] :=A[i+l]
;A[i+l] :=t;
End;
End;
При
сортировке методом "пузырька" выполняется N — 1 просмотров, на каждом
i-м просмотре производится N — i сравнений.
Общее количество С равно N* (N—1)/2,или O(N2).
Задания для
самостоятельной работы
1. Пример.
Дан массив 12 3 5 7 9 10. За один просмотр он становится отсортированным,
остальные просмотры ничего не дают. Исключить лишние просмотры.
2. Пример.
Массив 12 3 5 7 9 10 сортируется за один просмотр, а массив 5 7 9 10 12 3 — за
пять. Сократить количество просмотров можно путем смены направлений, т.е.
сначала в направлении —> получаем 5 7 9 10 3 12, а затем в направлении
<-- результат — 3 5 7 9 10 12. Итак, чередуем направления, пока массив не
будет отсортирован.
3.
Интегрируя задания 1 и 2, мы получаем при соответствующей технике
программирования красивый программный код с использованием рекурсии. Название
этого алгоритма — "шейкер-сортировка".
Сортировка
простыми вставками
Сортировка этим методом производится последовательно, шаг за шагом. На k-м.
шаге считается, что часть массива, содержащая первые k — 1 элементов,
уже упорядочена, то есть А [1] <= А [2] <= ... <=
А [k—1]. Далее берется k-й элемент,
и для него подбирается такое место в отсортированной части массива, что
упорядоченность не нарушается. То есть требуется найти такое j (0 <=
j <= k —1), что A[ j ] <= A[k}
< A [j + 1] (при j = 0 происходит только одно сравнение, если не
использовать "барьерную" технику). Затем выполняется вставка элемента
A [k] на место j, при этом происходит "сдвиг" массива
(элементов с j-го по k —1-й).
На
каждом шаге отсортированная часть массива увеличивается. Всего потребуется
выполнить N—1 шаг.
Рассмотрим этот процесс на примере.
Пусть требуется отсортировать массив из 10 элементов по возрастанию.
1-й
шаг.
13 б 8 11 3 1 5 9 15 7
Рассматриваем часть массива из одного элемента 13. Вставляем второй
элемент массива 6 так, чтобы упорядоченность сохранилась. Так как 6 < 13,
записываем 6 на первое место. Отсортированная часть массива содержит два
элемента (6 и 13).
2-й
шаг.
6
13 8 11 3, 1 5 ,9 15 7
Возьмем третий элемент массива 8 и подберем для него место в
упорядоченной части массива. 8 > 6 и 8 < 13, следовательно, его место —
второе.
3-й
шаг.
6 8
13 11 3 1 5 9 15 7
Следующий
элемент — 11. Он записывается в упорядоченную часть массива на третье место,
так как 11 > 8, но 11 < 13.
4-й
шаг.
6 8
11 13 3 1 5 9 15 7
Далее, действуя аналогичным образом, определяем, что 3 необходимо
записать на первое место.
5-й шаг.
3 6
8 11 13 1 5 9 15 7
По
той же причине 1 записываем на первое место.
6-й шаг.
1 3
6 8 11 13 5 9 15 7
Так
как 5 > 3, но 5 < б, то место 5 в упорядоченной части — третье.
7-й шаг.
1 3 5 6 8 11 13 9 15 7
Место числа 9 — шестое.
8-й шаг.
1 3
5 6 8 9 11 13 15 7
Определяем
место для предпоследнего элемента 15. Оказывается, что этот элемент массива уже
находится на своем месте.
9-й
шаг.
1 3
5 6 8 9 11 13 15 7
Осталось подобрать подходящее место для последнею элемента 7.
1 3
5 6 7 8 9 11 13 15
Массив
отсортирован полностью.
Процедура сортировки.
Procedure Sort;
Var k,j,x:Integer;
Begin
For k:=2 To N Do Begin;
x:=A[k]; j:=k-l;
While (j>0) And (x<A{j])
Do
Begin
A[j+l]:=A[j];Dec(j;);End;
А[j+1]:=x;
End;
End;
Оценим эффективность метода. Для массива,
например, 1 2 3 4 5 6 7 8 потребуется N — 1 сравнение (напомним, что мы
сортируем в порядке возрастания), а для массива 8 7 6 5 4 3 2 1 — N• (N — 1)/2,
или C=O(N2).
Задания для самостоятельной
работы
1. Убрать из процедуры сортировки переменную х,
а внутренний цикл записать в виде: While А[0] < А [j]. Подсказка. Массив А необходимо сделать типа
Array [O..NMax] Of Integer и k-и элемент записывать на 0-е место,
в качестве так называемого "барьерного элемента".
2. На момент вставки элемента с номером i
элементы массива с номерами от 1 до i — 1 отсортированы. Выберем из них
средний элемент (или один из двух средних) и сравним его с элементом А [i].
Если А [i] меньше этого элемента, то поиск места вставки следует
продолжать в левой половине, иначе в правой половине отсортированного массива.
Эта схема получила название сортировки бинарными вставками. Она предложена Дж.
Мочли в 1946 году в одной из первых публикаций по методам компьютерной
сортировка. Реализовать данную схему.
3. Д.Л. Шелл в 1959 году предложил следующую
модификацию метода — "сортировку с убывающим шагом". Покажем ее суть
на примере. Дан массив из 8 элементов. Разделим его на 4 группы по 2 элемента,
сортируем элементы в каждой группе. Затем группы увеличиваем в 2 раза, т.е. в
каждой группе становится по 4 элемента, и выполняем для них сортировку. И,
наконец, сортируем одну группу из 8 элементов.
1-й шаг.
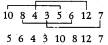
2-й шаг.

3-й шаг.
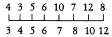
При
простых вставках мы перемешали элемент только в соседнюю позицию, а в этом
методе перемещаем на большие расстояния, что приводит к более быстрому
получению отсортированного массива и в конечном итоге к повышению эффективности
метода. Значения 4, 2,1 —количество групп (приращения) не являются догмой.
Можно выполнить сортировку при 5, 3, 1. Последний элемент должен быть равен 1.
Д,Кнут дает оценку метода при грамотном выборе приращений —
O(N1,2). Лучшим
считается выбор в качестве значений приращений взаимно простых чисел.
Реализовать "сортировку с убывающим шагом" для заданных значений
приращений.
Сортировка
слияниями
Прежде
чем обсуждать новый метод, рассмотрим следующую задачу. Объединить
("слить") упорядоченные фрагменты массива A [k],.... А [т]
и А [т 4- 1],..., A [q] в один A [k + 1], ..., A [q],
естественно, тоже упорядоченный (k
< т <= q). Основная идея решения состоит в попарном сравнении
очередных элементов каждого фрагмента, выяснении, какой из элементов меньше,
переносе его во вспомогательный массив D (для простоты) и продвижении по
тому фрагменту массива, из которого взят элемент. При этом следует не забыть
записать в D оставшуюся часть того фрагмента, который не успел себя
"исчерпать".
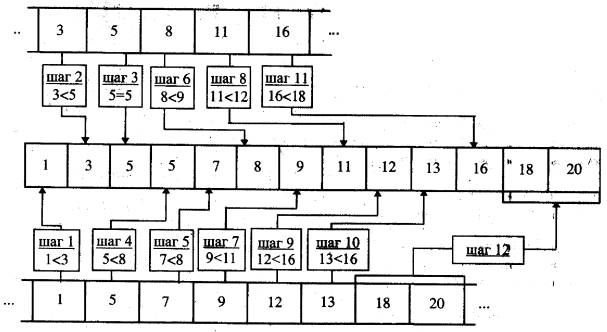
Пример. Пусть первый фрагмент состоит из 5 элементов: 3 5 8 11
16, а второй — из 8: 1 5 7 9 12 13 18 20. Рисунок на с. 10 иллюстрирует логику
объединения фрагментов.
Procedure SI(k,m,q:Integer);
{Массив А глобальный}
Var i, j, t :
Integer;
D:MyArray;
Begin
i:=k; j: =m+1; t:=l;
While (i<=m) And (j<=q) Do
Begin
{Пока не закончился хотя бы один
фрагмент.}
If A[i]<=A[j] Then
Begin D[t]:=A[i]; Inc( i ); End
Else Begin
D[t] :=A[j ]; Inc( j );
End;
Inc(t);
End; {Один из фрагментов обработан
полностью, осталось перенести в D остаток другого фрагмента.}
While i<=m Do
Begin D[t]:=A[i]; Inc (i);
Inc(t) End;
While j<=q Do
Begin D(t]:=A[j];Inc(j);
Inc(t) End;
For i:=l To t-1 Do A[k+I-1]:=D[i];
End;
Параметр m из заголовка процедуры можно
убрать. Мы "сливаем" фрагменты одного массива А. Достаточно оставить
нижнюю и верхнюю границы фрагментов, т.е. — Sl(к, q: Integer), где k — нижняя, а q
— верхняя границы. Вычисление т (эта переменная становится локальной)
сводится к присвоению: т:= k + (q — k) Div 2. При этом
уточнении приведем процедуру сортировки. Первый вызов процедуры — Sort(1,
N).
Procedure Sort(i,j:Integer);
Var t:Integer;
Begin
If i>=j Then Exit;
{Обрабатываемый
фрагмент массива из одного элемента.}
If j-i=l Then Begin If A[j]<A[i] Then
Begin{Обрабатываемый фрагмент массива из двух элементов.}
t:=A[i];A[i] :=A[j];A[j] :=A[i];
End;
End
Else Begin
Sort (i,i+(J-i) Div 2);
{Разбиваем заданный фрагмент на два.}
Sort(i+(j-i) Div 2+1,j);
Sl(I,j);
End;
End;
Метод
слияний — один из первых в теории алгоритмов сортировки. Он предложен Джоном
фон Нейманом в 1945 году. В этом алгоритме наглядно реализован принцип
"разделяй и властвуй". Рекомендуется проделать с учащимися
"ручную" трассировку работы процедуры на различных примерах. Это,
во-первых, позволит в очередной раз глубже понять суть принципа и, во-вторых,
проверить понимание и усвоение темы "рекурсия". Эффективность алгоритма,
по Д. Кнуту, составляет С= O(N• Log2N).
Задания для
самостоятельной работы
1. Дан массив 7 9 13 1 8 4 10 11 5 3 6 2. Видим возрастающий
участок 7 9 13, а справа, если читать справа налево, есть участок 2 6. Слияние
этих двух фрагментов массива дает 2 6 7 9 13. А затем "сливаем" 1 8 и
3 5 11, получаем 1 3 5 8 11. Записываем в массив и получаем: 2 6 7 9 13 4
10 11 8 5 3 1. Обратите внимание на то, как записываем!
Продолжим. Поскольку средний участок 410 "сливать" не с чем,
рассмотрим его как два — 410 и 10 (т.е. прочитаем его в двух направлениях).
Если с первыми фрагментами 2 6 7 9 13 и 1 3 5 8 11 все ясно, то вторые 4 10 и
10 перекрываются. Необходимо учесть сей факт и не дублировать 10 при записи в
массив. Получаем: 1 2 3 5 6 7 8 9 11 13 10 4. Последнее
"слияние" дает 1 2 3 4 5 6 7 8 9
10; 11 13. Массив отсортирован. Этот метод называется у Д. Кнута “сортировкой естественным двухпутевым
слиянием”
2. 'Изменим схему выбора
участков для "слияния". Не будем искать монотонные участки, а
работаем с участками фиксированной длинны (“простое двухпутевое слияние”).
Пример.
Исходный
массив:
13 1 7 5 4 3 9 10 6 19 14 16 23 2 4 8.
1-й
шаг (длина 1).
8 13 2 7 4 16
9 19 10 6 14 3 23 5 4 1.
2-й
шаг (длина 2).
14 813 3 4 14
16 19 10 9 6 23 7 5 2.
3-й
шаг (длина 4).
1 2 4 5 7 8 13 23
1916 14 10 9 6 4 3.
4-й
шаг (длина 8).
1 2 3 4 4 5 6 7
8 9 10 13 14 16 19 23.
Реализовать данный алгоритм
сортировки. Размер массива не всегда совпадает с числом, равным степени двойки.
3. Интеграция алгоритма простых вставок с предыдущим
упражнением дает новое задание. Разделим массив на участки определенной длины.
Каждый из них отсортируем с помощью алгоритма простых вставок, а затем
используем "простое двухпутевое слияние". Так, в предыдущем примере
слияние используется на 3-м и 4-м шагах, а первые два заменяются работой по
алгоритму простых вставок.
4. Обобщите предыдущие задание
заменой слова “двухпутевое” на “трехпутевое“
( “четырехпутевое” ,..., "k-путевое" ). Значительное увеличению программного
кода при этом недопустимо.
Примечание.
В этом параграфе, как и
во всех предыдущих, мы работаем с целочисленным массивом. Если использовать для
хранения данных не массив, а однонаправленный или двунаправленный списки, то
все задания становятся хорошей базой для изучения этих типов данных.
Быстрая сортировка
Данный метод был предложен Ч.Э.Р.
Хоаром в 1962 году. В общем случае его
эффективность достаточно высока (слова "в
общем случае" означают, что можно специально
подобрать такие наборы данных, на которых данная
сортировка будет малоэффективна), поэтому автор
назвал его "быстрой сортировкой".
Опишем идею метода. В исходном массиве А
выбирается некоторый элемент X (его называют
"барьерным"). Нашей целью является запись Х
"на свое место" в массиве, пусть это будет
место k, такое, чтобы слева от Х были элементы
массива, меньшие или равные X, а справа — элементы
массива, большие X, т.е. массив А будет иметь вид:
(A[1], A[2], ..., A[k - 1] ), A[k] = (X), (A[k + 1], ...,
A[n]
).
В результате элемент A [k] находится на
своем месте и исходный массив А разделен на две
неупорядоченные части, барьером между которыми
является элемент А [k]. Далее требуется
отсортировать полученные части тем же методом до
тех пор, пока в каждой из частей массива не
останется по одному элементу, то есть пока не
будет отсортирован весь массив.
Пример.
Исходный массив состоит из 8 элементов: 8 12 3 7 19 11 4
16. В качестве барьерного элемента возьмем
средний элемент массива (7). Произведя
необходимые перестановки, получим: (4 3) 7 (12 19 11 8 16);
теперь элемент 7 находится на своем месте.
Продолжаем сортировку.
Левая часть:
Правая часть:
(3) 4 7 (12 19 11 8 16)
3 4 7 (8) 11 (19 12 16)
3 4 7 (12 19 11 8 16)
3 4 7 8 11 (19 12 16)
3 4 7 8 11 12 (19 16)
3 4 7 8 11 12 (16) 19
3 4 7 8 11 12 16 19
Из описания алгоритма видно, что он может
быть реализован посредством рекурсивной
процедуры, параметрами которой являются нижняя и
верхняя границы изменения индексов сортируемой
части исходного массива. Приведем процедуру
быстрой сортировки (автора первоначального
текста установить, по-видимому, не
представляется возможным, поскольку эта
процедура встречается в различных источниках):
Procedure Quicksort (m, t: Integer);
Var i , j , x , w: Integer;
Begin
i:=m; j:=t; x:=A[ (m+t) Div'2];
Repeat
While A[i]<x Do Inc(i);
While A[j]>x Do Dec(j);
If i<=j Then Begin w:=A[i]; A[i]:=A[j];
A[jl:=w; Inc(i); Dec(j) End
Until i>j;
If m<j Then Quicksort(m, j);
If i<t Then Quicksort(i,t),
End;
Простая процедура, но
возникает "тысяча и один вопрос".
Соответствуют ли результаты работы процедуры
рассмотренному выше примеру, естественно, при
тех же исходных данных? Оказывается, нет. Лучше,
если учащиеся убедятся в этом самостоятельно.
Результаты работы процедуры выглядят следующим
образом (первые два столбца содержат параметры
процедуры, третий — массив А):
m |
t |
A |
| 1 |
8 |
4 12 3 7 19 11 8 16 |
| 1 |
8 |
4 7 3 12 19 11 8 16 |
| 1 |
3 |
4 3 7 12 19 11 8 16 |
| 1 |
2 |
3 4 7 12 19 11 8 16 |
| 4 |
8 |
3 4 7 8 19 11 12 16 |
| 4 |
8 |
3 4 7 8 11 19 12 16 |
| 4 |
5 |
3 4 7 8 11 19 12 16 |
| 6 |
8 |
3 4 7 8 11 12 19 16 |
| 7 |
8 |
3 4 7 8 11 12 16 19 |
Продолжим наши рассуждения.
В процедуре есть сравнение
If i<=j Then <перестановка элементов A[i] и A[j] >
Получается, что при равенстве мы выполняем
перестановку элементов массива. Заменим условие
на следующее: i < j. Результат — бесконечная
работа процедуры ("зацикливание").
Рекурсивный вызов процедуры осуществляется при
выполнении условия т < j. А если просто
вызвать? Результат не замедлит сказаться.
Произойдет переполнение стека адресов возврата.
Цикл
repeat ... Until i>j;
работает и при i = j, что кажется
неестественным. Заменим условие на следующее: i
>= j. Что произойдет? Заключительным
"аккордом" обсуждения процедуры может быть
предложение написать код, соответствующий
примеру, рассмотренному в начале параграфа.
Оценим эффективность метода. Предположим,
что размер массива равен числу, являющемуся
степенью двойки (N = 2q), и при каждом разделении
элемент Х находится точно в середине массива. В
этом случае при первом просмотре выполняется N
сравнений и массив разделится на две части
размерами 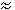 N/2. Для каждой из этих частей
выполняется N/2 сравнений и т.д. В конечном итоге
N/2. Для каждой из этих частей
выполняется N/2 сравнений и т.д. В конечном итоге
С = N + 2 • (N/2) + 4 • (N/4) + ... + N • (N/N) = 0(N •
logN).
Если N не является степенью двойки, то оценка
будет иметь тот же порядок. Для экзотического
случая — Х на каждом шаге оказывается самым
маленьким или самым большим элементом в
рассматриваемой части массива — С = 0(N2), ибо на
каждом шаге размер сортируемой части массива
уменьшается лишь на единицу.
Задания для самостоятельной работы
1. Следует отметить,
что данный алгоритм является затратным с точки
зрения использования оперативной памяти.
Замените рекурсивную схему реализации логики на
нерекурсивную и оцените значение N, при котором
ваша программа в рекурсивной реализации не будет
компилироваться по этой причине. Разумеется,
такую оценку можно сделать и при рекурсивной
реализации, просто тип ошибки будет другой.
Вводить исходные данные с клавиатуры или вручную
создавать входной файл — утомительное занятие.
Разумная лень — двигатель прогресса, поэтому для
выполнения задания необходимо написать
специальную программу создания входного файла с
данными.
2. Считается, что выбор элемента Х
случайным образом оставляет среднюю
эффективность неизменной при всех типах
массивов (упорядоченный, распределенный по
какому-то закону и т.д.). Реализуйте эту идею.
Пирамидальная сортировка
Данный метод был предложен
Дж.У.Дж. УИЛЬЯМСОМ и Р.У. Флойдом в 1964 году.
Элементы массива А образуют пирамиду, если для
всех значений i выполняются условия: A [i]
<= А [2 • i] и А [i] <= А [2 • i + 1
].
Пример. Элементы массива 8 10
3 6 13 9 5 12 не образуют пирамиду (А[1] > А [3], А
[2] > А [4] и т.д.), а элементы массива
3 6 5 10 13 9 8 12 — образуют.
Очевидно, что элементы правой половины
массива A [N/2+1 .. N] независимо от их значений
образуют пирамиду.
Предположим, что нам необходимо
отсортировать элементы массива А (8 10 3 6 13 9 5 12) по
невозрастанию.
Идею сортировки поясним с помощью следующей
таблицы (курсивом выделена часть элементов
массива, образующих пирамиду, жирным шрифтом —
отсортированная часть массива).
№ шага |
A |
Комментарии |
1
2
3
4
5 |
8 10 3 6 13 9 5 12
8 10 3 6 13 9 5 12
8 10 3 6 13 9 5 12
8 6 3 10 13 9 5 12
3 6 5 10 13 9 8 12 |
Строим пирамиду из
элементов A с1-го по 8-й
|
| 6 |
12 6 5 10 13 9 8 3 |
Меняем местами 1-й и 8-й
элементы |
7
8
9
10 |
12 6 5 10 13 9 8 3
12 6 5 10 13 9 8 3
12 6 5 10 13 9 8 3
5 6 8 10 13 9 12 3 |
Строим пирамиду из
элементов A с 1-го по 7-й
|
| 11 |
12 6 8 10 13 9 5 3 |
Меняем местами 1-й и 7-й
элементы |
12
13
14
15 |
12 6 8 10 13 9 5 3
12 6 8 10 13 9 5 3
12 6 8 10 13 9 5 3
6 10 8 21 13 9 5 3 |
Строим пирамиду из
элементов A с 1-го по 6-й
|
| 16 |
9 10 8 12 13 6 5 3 |
Меняем местами 1-й и 6-й
элементы |
17
18
19 |
9 10 8 12 13 6 5 3
9 10 8 12 13 6 5 3
8 10 9 12 13 6 5 3 |
Строим пирамиду из
элементов A с 1-го по 5-й
|
| 20 |
13 10 9 12 8 6 5 3 |
Меняем местами 1-й и 5-й
элементы |
21
22
23 |
13 10 9 12 8 6 5 3
13 10 9 12 8 6 5 3
9 01 13 12 8 6 5 3 |
Строим пирамиду из
элементов A с 1-го по 4-й
|
| 24 |
12 10 13 9 8 6 5 3 |
Меняем местами 1-й и 4-й
элементы |
25
26 |
12 10 13 9 8 6 5 3
10 12 13 9 8 6 5 3 |
Строим пирамиду из
элементов A с 1-го по 3-й
|
| 27 |
13 12 10 9 8 6 5 3 |
Меняем местами 1-й и 3-й
элементы |
28
29 |
13 12 10 9 8 6 5 3
12 13 10 9 8 6 5 3 |
Строим пирамиду из
элементов A с 1-го по 2-й
|
| 30 |
13 12 10 9 8 6 5 3 |
Меняем местами 1-й и 2-й
элементы |
В конечном итоге массив
отсортирован.
Пусть мы умеем строить пирамиду из элементов
массива А с индексами от 1 до q (процедура Руram
(q) ), тогда процедура сортировки имеет вид:
Procedure Sort;
Var t,w:Integer;
Begin
t:=N;
Repeat
Pyram(t);{Строим пирамиду из t
элементов.}
w:=A[1];A[1]:=A[t];A[t]:=w;
Dec (t)
Until t<2
End;
Из таблицы мы видим, что процесс
построения пирамиды начинается с конца массива.
Посдедние q div 2 элементов являются пирамидой
по той причине, что удвоение индекса выводит нас
за пределы массива. А затем берется очередной
справа элемент из "непирамидальной" части и
"проталкивается" по "пирамидальному"
массиву до тех пор, пока он не будет меньше
элемента с удвоенным индексом (по отношению к
индексу рассматриваемого элемента) и следующего
за ним элемента. Процесс продолжается до тех пор,
пока мы "не поставим" на своё место первый
элемент массива. Приведем текст процедуры.
Procedure Pyram(q:Integer);
Var r, i, j,v:Integer;
Begin
r:=q Div 2+1;{Эта часть массива является
пирамидой.}
While г>1 Do Begin{Цикл-по элементам
массива, для которых необходимо найти место в
пирамиде.}
Dec(г);
i:=r; v:=A[i];{Индекс,
рассматриваемого элемента и сам элемент.}
j:=2*i;{Индекс элемента, с
которым происходит сравнение.}
pp:=False;{Считаем, что для
элемента не найдено место в пирамиде.}
While (J<=q) And Not pp Do Begin
If j<q
Then If A[j]>A[j+l] Then Inc(j);{Сравниваем с меньшим
элементом.}
If
v<=A[j] Then pp:=true {Элемент находится на своем месте.}
else
begin A[i]:=A[j]; i:=j; j:=2*i end {Переставляем элемент и идем
дальше по пирамиде.}
End;
A[i]:=v
End;
End;
Метод имеет эффективность порядка
O(N • logN). Однако если рассмотреть вышеприведенную
логику, то окажется, что ее оценка O(N2 • logN). При
сортировке процедура Pyram вызывается N — 1 раз. Эта
процедура состоит из двух вложенных циклов
сложности N и — logN. Итак, упорядочивание одного
элемента требует не более logN действий,
построение полной пирамиды N • logN действий. В
вышеприведенной логике после каждой
перестановки элементов вновь строится пирамида
для оставшихся элементов массива. А зачем?
Пирамида почти есть. Требуется только
"протолкнуть" верхний элемент на свое место
(т.е. строки таблицы с номерами 7—9, 12—14, 17—18,21—22,
25, 28, вообще говоря, избыточны). Выделим
"проталкивание" одного .элемента в
отдельную процедуру Pr (r,q) , где r — номер
проталкиваемого элемента, q — верхнее
значение индекса.
Procedure Рг(r,q:Integer);
Var r, i, j,v: Integer;
pp:boolean;
Begin
i:=r; v:A[i];{Индекс рассматриваемого
элемента и сам элемент.}
j:=2*i;{Индекс элемента, с которым
происходит сравнение.}
pp:=False;{Считаем, что для элемента
не найдено место в пирамиде.}
While (j<=q) And Not pp Do Begin
If j<q Then If
A[j]>A[j+l] Then Inc(j);{Сравниваем с меньшим элементом.}
If v<=A[j] Then pp:=true
{Элемент находится на своём месте. }
else begin A[i]
:=А[j]; i:=j; j:=2*i end {Переставляем элемент и идем
дальше по пирамиде.}
End;
A[i]:=v
End;
Какие изменения
требуется внести в процедуру Sort?
Procedure Sort;
Var t, w, i:Integer;
Begin
t:=N Div 2+1; {Эта часть массива является
пирамидой.};
For i:=t-l DownTo 1 Do Pr(i,N);{Строим
пирамиду(только один раз).}
For i:=N DownTo 2 Do Begin ;
w:=A[1] ;A[1]:=A[i] ;A[i]:= w; {Меняем
местами 1-й и i-й элементы.}
Pr(1,i-l) {Проталкиваем 1-й
элемент.}
End
End;
Примечйние. Понижение
сложности алгоритма N^2 • logN до N• logN может быть
предметом самостоятельной работы с элементами
соревнования.
Задания для самостоятельной работы
1. Изменить алгоритм так,
чтобы элементы массива А сортировались в порядке
неубывания.
2. Представим элементы нашего
массива в виде бинарного дерева так, как показано
на левой части рисунка. В результате построения
пирамиды на элементах массива с 1-го по 8-й дерево
преобразуется к виду, показанному на Правой
части рисунка. После этого меняется содержимое
определенных узлов дерева и верхний элемент
"проталкивается" по пирамиде. Продолжите
эти рисунки для всех оставшихся шагов
сортировки.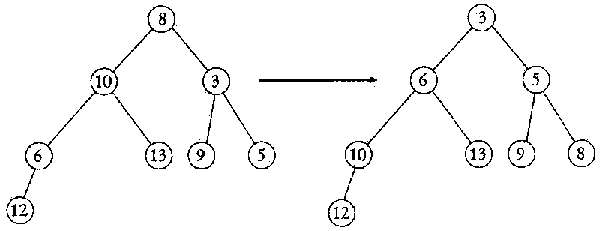
3. Разработать программу
пирамидальной сортировки для случая, когда для
хранения данных используется не массив, а
бинарное дерево.
4. Для хранения данных используется
не массив, а список (однонаправленный или
двунаправленный) .— "сортировка списка".
Разработать программу пирамидальной сортировки
для этого случая.
5. Приведем разбор задачи "Дворец
черепашек". Рекомендуется первоначально
предложить ребятам решить ее самостоятельно, а
затем обсудить и разобрать с учащимися.
Условие задачи. Много, очень
много черепашек живет в огромном дворце со всеми
удобствами, кроме одного. Им приходится ползать за водой к родниковому источнику. Дорога
до источника прямая, ее длина М метров. В
некоторый момент
времени на дороге находится N черепашек. Часть из
них ползет в сторону дворца, часть — к источнику.
Все
черепашки ползут с одинаковой скоростью (1
метр в час).
Требуется найти:
• общее количество встреч черепашек в
пути;
• время последней встречи.
Входные данные (файл Input.Txt). В первой
строке записаны значения М и N, а затем N строк, в
каждой из которых записаны Х i (1 <= i<= N) —
координата черепашки и буква "Д" или "И"
(направление движения черепашки). Все координаты
X i — вещественные числа и различны.
Выходные данные (файл OutputTxt). В первой
строке записывается количество встреч, во второй
— время последней встречи (с точностью до пяти
знаков). При отсутствии встреч выводится
сообщение: "NO MEETINGS".
Ограничения. 1<= N<= 30 000, время
решения — 10 секунд.
Идея решения основана на
сортировке массива координат черепашек с
одновременной перестановкой соответствующих
признаков "Д" и "И". Затем для решения
первой проблемы необходимо подсчитать для
каждой черепашки, ползущей к источнику, число
черепашек, имеющих большее значение координаты и
ползущих во дворец. Сумма этих значений является
ответом. Для ответа на второй вопрос необходимо
найти самую правую черепашку, ползущую к
источнику, и самую левую, возвращающуюся во
дворец. Расстояние между ними, деленное на два,
дает время последней встречи. Итак, задачу нельзя
назвать особенно сложной. Рассмотрим
программную реализацию алгоритма.
Максимальное количество координат
30 000, причем вещественных значений. А это 4 байта,
умноженные на 30 000, или 120 000 байт. При стандартной
реализации в системе программирования Паскаль
оперативной памяти явно не хватит, для задачи в
качестве сегмента данных выделяется несколько
меньше 64 Кб, поэтому необходимо использовать
"кучу" (область оперативной памяти для
динамических переменных). Объем "кучи"
позволяет это сделать. Второе соображение при
выборе алгоритмаследует из ограничений на время
решения задачи. Алгоритмы с квадратичной
эффективностью не подходят, но мы знаем три
алгоритма со сложностью O(N• logN). Более
эффективные мы не изучали.
Учитывая этот факт и первое соображение,
выбираем алгоритм пирамидальной сортировки,
причем данные о местоположении черепашек —
координаты следует размещать в "куче".
Структуры данных.
Const MaxN=30000;
Trg=12; {212 -
размер блока, для хранения всех возможных
координат черепашек потребуется 8
блоков (последний используется
на одну треть).}
Eps=le-6;{Точность вычислений.}
InputFile='Input.TxT' ;
OutputFile='Output.TxT'
;
_NoMeet='NO MEETINGS';
TypeBMas=Array[0..4095]
Of Real;
TukReal=^Real;
Var A: Array[0..(MaxN-1) Div 4095] Of ^BMas;
{Массив указателей (8 элементов) на блоки по 4096 вещественных чисел.}
Ind: Array[O..MaxN-l] Of
Char;{Направления движения черепашек.}
N, sca: Word;{Количество
черепашек и та их часть, которая ползет ко
дворцу.}
rsa: LongInt;{Ответ на 1-й
вопрос.}
М, rsb: Real;{Расстояние и
ответ на 2-й вопрос.}
rs: Boolean;{Признак того, что
есть решение.}
Приведем вначале процедуру вывода
результатов и основную программу, чтобы было
ясно, к чему мы стремимся.
Procedure Done;
Begin
Assign(Output, OutputFile) ;
Rewrite(Output) ;
If rs Then Begin WriteLn (rsA); WriteLn (rsB: 0:5) End
Else WriteLn(_NoMeet);
Close(Output)
End;
Begin Init; Solve; Done End.
Прежде чем уточнять логику,
научимся работать с массивом координат
черепашек А. Функция чтения элемента из массива А
по его номеру имеет вид:
Function GetA(p: Word): Real;
Begin
GetA:=A[p shr TRg]^[p And (4095)] {p делим на 212 (сдвиг
вправо на 12 разрядов) и выделяем из р 12 младших
разрядов.}
End;
Запись вещественного числа в
массив А программируется аналогичным образом.
Procedure SetA(p: Word; Const aa: Real);
Begin
A[p shr TRg]^[p And (4095)]:=aa
End;
Теперь мы можем привести процедуру Init.
Procedure Init;
Var i: Integer; bb: Real;
Begin
FillChar(A, SizeOf(A), 0) ;
sca:=0;
Assign(Input, InputFile) ;
Reset(Input) ;
Read(M, N); Dec(N);
For i:=Q To N Do Begin
If A[i shr TrG]=nil Then New(A[i shr TrG]) ;
Read(bb) ;
SetA(i, bb);
Read(Ind[i]) ;
While Not (UpCase(Ind[i] ) In [ 'Д', 'И'
] ) Do Read (Ind[i]) ;
If Ind[i]='Д' Then Inc(sca) {Общее
количество черепашек, ползущих во дворец.}
End;
Close(Input)
End;
Обмен значениями двух элементов
массива А с одновременной перестановкой
соответствующих элементов массива Ind имеет
вид (используется в процедуре сортировки):
Procedure SwapDD (Const ас, bc: Word);
Var aa, bb: TukReal;
с: Real;
cc: Char;
Begin
aa:=@A[ac shr TRg]^[ac And (4095)];{B переменной аа
адрес элемента массива, данный прием позволяет
сократить длину записи
последующих операторов.}
bb:=@A[bc shr TRg]^[bc And (4095)];
с:=аа^; аа^:=bb^; bb^:=c;
cc:=Ind[ac]; Ind[ac] :=Ind[bc]; Ind[bc] :=cc
End;
Процедуру пирамидальной
сортировки (Sort) приводить не будем, она описана
выше. Следует только помнить, что для сравнения
вещественных чисел лучше использовать функцию
типа:
Function More (Const a, b: Real): Boolean;
Begin More:=a-b>Eps End;
Перейдем к
основной процедуре.
Procedure Solve;
Begin
Sort;{Пирамидальная сортировка.}
CheckA;{Решение 1-й части задачи.}
If (sca=0) Or (sca=N+l) Or (rsA=0) Then rs:=False {Heт
черепашек, ползущих ко дворцу, нет черепашек,
ползущих к источнику, нет ни одной встречи между черепашками. В любом из этих
случаев нет решений и необходимо выводить соответствующее сообщение.}
Else Begin rs:=True;CheckB End {Решаем 2-ю часть задачи.}
End;
Процедура решения первой части
задачи имеет вид:
Procedure CheckA;
Var i, lfa: LongInt;
Begin
rsА:=0; 1fa:=sca;{Текущее
значение количества черепашек, ползущих во
дворец.}
For i:=0 То N Do
If Ind[i]='Д' Then Dec (lfa)
{Черепашки, ползущие к
источнику и находящиеся ближе к источнику, чем
эта черепашка, ползущая во дворец уже не
встретятся с ней.}
Else lnc (rsA, Ifa)
{Если черепашка ползет к
источнику, то она встречается со всеми
черепашками, находящимися ближе ее к источнику и
ползущими во
дворец.}
End;
Для второй части задачи процедура выглядит
еще проще.
Procedure CheckB;
Var i: LongInt; If, rg: Real;
Begin
i:=0;
While Ind[i]='Д' Do Inc(i);{Находим координаты 1-й
черепашки, ползущей к источнику.}
if:=GetA(i); i:=N;
While Ind[i]='И' Do Dec(i);{Находим координату
последней черепашки, ползущей во дворец.}
rg:=GetA(i); rsB:=,(rg-lf)/2
End;
Цель достигнута. Решение есть, но тема
отнюдь не исчерпана. Продолжим ее обсуждение.
Очевидным является шаг по замене пирамидальной
сортировки на метод Хоара или слияния. А затем?
Пусть каждая черепашка ползет со своей
скоростью, допустим, возраст у них разный. Если до
этого мы решали задачу для регулярной структуры
(левая часть рисунка) — угловой коэффициент у
всех прямых одинаковый, то при данной
модификации задача соответствует структура,
изображенная на правой части рисунка.
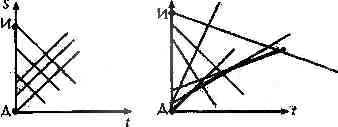
На правой части рисунка более
"жирными" линиями выделена ломаная,
проходящая по участкам прямых, соответствующих
черепашкам, ползущим из дворца. Требуется
найти самую правую точку пересечения прямых,
описывающих перемещения черепашек от источника
к дворцу, с этой ломаной.
Продолжим наши рассуждения о задаче
(усложнения). Пусть нет черепашек, ползущих от
источника, а черепашки, достигающие источника,
остаются у него и пьют воду не один раз, а с
некоторой периодичностью (для каждой черепашки
она своя). При этом каждая черепашка за каждый
подход пьет разное количество воды. Например,
имеются две черепашки. Первая пьет 7, 5, 3, 1 литров
воды, с периодичностью в 6 единиц времени, вторая
— 11, 7, 3, с периодичностью 5 единиц времени.
Известно количество воды в источнике (V).
Определить, какая из черепашек будет пить
последней, если воды в источнике, не хватит, или
количество оставшейся в источнике воды для
случая, когда все черепашки могут удовлетворить
свою жажду.
Цель наших модификаций (рассуждении)
сводится к следующему: во-первых, в оперативной
памяти (включая "кучу" ) не должно хватать
места для хранения всех данных, во-вторых, из всех
алгоритмов сортировки с эффективностью O(N • logN)
придется использовать только пирамидальную
сортировку.
Попытаемся рассмотреть возможные схемы
решения задачи. Первый вариант. Просчитаем все
значения времени питья черепашек, а затем
отсортируем и выполним требуемый подсчет.
Оперативной памяти не хватит. Второй вариант.
Можно хранить для каждой черепашки только время
ее очередного питья, выбирать минимальное
значение и корректировать массив времен.
Сложность решения порядка О(N2), оно не должно
проходить по временным ограничениям. Третий
вариант. Хранить упорядоченный массив времен.
Брать первый элемент — минимальный, а затем с
использованием бинарного поиска вставлять
очередной элемент. В этом случае потребуется
сдвиг элементов массива, и окончательная оценка
сложности имеет порядок О(N2). Четвертый вариант.
Хранить данные по временам питья черепашек в
виде пирамиды. После изъятия верхнего элемента
время следующего приема воды для этой черепашки
проталкивается по пирамиде. Этот вариант не
требует дополнитадаюй памяти и имеет сложность
O(N • logN).
Примечание. На данном примере
мы старались показать процесс работы над
задачей, от ее простого варианта (а мы начали не с
самого простого) до олимпиадного уровня.
2. Поиск данных
Линейный поиск
Основной вопрос задачи поиска: где
в заданной совокупности данных находится
элемент, обладающий заданным свойством?
Большинство задач поиска сводится к простейшей
— к поиску в массиве элемента с заданным
значением. Рассмотрим именно эту задачу. Пусть
требуется найти элемент Х в массиве А. В
данном случае известно только значение
разыскиваемого элемента, никакой дополнительной
информации о нем или о массиве, в котором
производится поиск, нет. Наверное, единственным
способом является последоаательныйпросмотр
массива и сравнение значения очередного
рассматриваемого элемента массива с X. Напишем
фрагмент:
For i:=1 To N Do If A[i]=X Then k:=i;
В этом цикле находится индекс
последнего элемента А, равного X, при этом
массив просматривается полностью. А если
требуется найти индекс первого элемента, равного
X?
For i:=N DownTo 1 Do If A[i]=X Then k:=i;
А если исключить лишние проверки?
Совпадение найдено, зачем делать "пустую"
работу?
i:=I;
While (i<=N) And (A[i]<>X) Do Inc(i);
If i=N+l Then <X нет в A> Else <значение i указывает на
место совпадениям>
В этом фрагменте решается задача
поиска первого совпадения. Для нахождения
последнего совпадения требуется изменить совсем
немного:
i:=N;
While (i>0) And (A[i]<>X) Do Dec(i);
If i=0 Then <X нет в A> Else <значение i указывает на
место с6впадения>;
Примечания. 1.Необходимо
обратить внимание на порядок проверки
составного условия цикла. Предполагается, что
второе условие не проверяется, если результат
логического выражения определен после проверки
первого условия. В противном случае возникает
ошибка из-за выхода индекса за границы массива.
2. Для контроля удобно использовать директиву
{$R+).
3. В качестве упражнения можно заменить цикл
While на цикл Repeat ... Until.
Вспомним технику использования
"барьерных" элементов из темы
"Сортировка" и применим ее для изучения
поиска элемента в массиве. Это требует
увеличения размерности массива А на единицу:
Type MyArray=Array[0..NMax] Of Integer;
или
MyArray=Array[l..NMax+l) Of Integer; Var A:MyArray,
Значение Nmax определяется в
разделе констант. Найдем первое вхождение
элемента Х в массив:
i:=l;A[N+l]:=Х;
While A[i] <> X Do Inc(i);
If i=N+l Then <X нет в A> Else <начение i указывает на
место совпадения>;
Для поиска последнего совпадения
цикл записывается следующим образом (используем
1-й вариант описания массива А):
i:=N;A[0]:=Х;
While A[i] <> X Do Dec(i);
If i=0 Then <X нет в A> Else Оначение i указывает на
место совпадения>;
Очевидно, что число сравнений
зависит от местонахождения искомого элемента. В
среднем количество сравнений равно (N + 1) div 2, в
худшем случае, когда элемента нет в массиве, N
сравнений. Эффективность поиска — O(N).
Задания для самостоятельной работы
1. Во входном файле дан
массив А и массив из элементов, поиск которых
будет осуществляться в массиве А. Изменить
массив А таким образом, чтобы суммарное
количество сравнений при поиске элементов было
минимальным.
Примечание. По данным из второго
массива формируются частоты поиска каждого
элемента, и элементы массива А сортируются в
порядке убывания значений этих частот ("метод
перемещения в начало"). На основе этой задачи
можно провести небольшое исследование.
Необходимо найти значения N, при которых массивы
не помещаются в оперативную память, отводимую
под программу, или не помещаются и в "кучу".
Если еще добавить и ограничения на время решения,
то одного занятия для решения задачи может
оказаться недостаточным.
2. Даны массив А и число X.
Переставить элементы массива таким образом,
чтобы вначале были записаны элементы, меньшие
или равные X, а затем— большие или равные X.
Переставить элементы массива таким образом,
чтобы вначале были записаны элементы, меньшие X,
затем равные Х и, наконец, большие X.
Примечание. Указанные
перестановки следует сделать за один просмотр А
и без использования дополнительных массивов.
Бинарный поиск
Как было отмечено выше, если
никаких дополнительных сведений о массиве, в
котором хранятся данные, нет, то ускорить поиск
нельзя. Если же заранее известна некоторая
информация о данных, среди которых ведется поиск,
например, известно, что массив данных
отсортирован, то удается сократить время поиска,
используя бинарный (двоичный, дихотомический,
методом деления пополам — все это другие
названия алгоритма, основанного на той же идее)
поиск.
Итак, требуется определить место Х в
отсортированном (например, в порядке неубывания)
массиве А. Идея бинарного метода стара как
мир. Еще древние греки говорили — "разделяй и
властвуй". Вот и делим, делим пополам и
сравниваем Х с элементом, который находится
на границе этих половин. Отсортированность А
позволяет по результату сравнения со средним
элементом массива исключить из рассмотрения
одну из половин. А остальное — технические
детали, требующие пунктуальности —
необходимого, но, к счастью, недостаточного
навыка специалиста по информатике.
Пример. Пусть Х = б, а массив А
состоит из 10 элементов:
3 5 б 8 12 15 17 18 20 25.
1-й шаг. Найдем номер среднего элемента: т=[(1+10)/2]
= 5.
Так как 6 < А [5], далее можем рассматривать только
элементы, индексы которых меньше 5:
3 5 6 8 12 15 17 18 20 25.
2-й шаг. Рассматриваем лишь первые 4 элемента
массива, находим индекс среднего элемента этой
части
т =[(1+4)/2] = 2, 6 > А [2], следовательно, первый и
второй элементы ,из рассмотрения исключаются:
3 5 6 8 12 15 17 18 20 25.
3-и шаг. Рассматриваем два элемента, значение т
=[(3+4)/2] = 3:
3 5 6 8 12 15 17 18 20 25.
А [3]= б. Элемент найден, его номер — 3.
Программная реализация бинарного
поиска может иметь следующий вид.
Procedure Search;
Var i,j,m:Integer; f:Boolean;
Begin
i:=1; j:=N;{На первом шаге
рассматривается весь массив.}
f:=False;(Признак того, что Х не найден.}
While (i<=j) And Not f Do Begin
m:=(i+j) Div 2;
{Или m:=i+.(j-i) Div 2; , так
как i+(j-i) Div 2= (2*i+(j-i)) Div 2=(i+j) Div 2.}
If A[m]=X Then f:=True {Элемент
найден, поиск прекращается.}
Else If A[m]<X Then i:=m+l
{Исключаем из рассмотрения левую часть А.}
Else j:=m-l{Правую часть.}
End
End;
Предложим еще одну, рекурсивную,
реализацию изучаемого поиска. Значением
переменной t является индекс искомого
элемента или ноль, если элемент не найден.
Procedure Search (i,j:Integer;Var t:Integer);
{Массив А и переменная Х глобальные величины}
Var m:Integer;
Begin
If i>j Then t:=0 Else Begin m:=(i+j) Div 2;
If
A[m]<X Then Search(m+1,j,t) Else
If
A[m]>X Then Search(i,m-l,t) Else t:=m
End
End;
Каждое сравнение уменьшает диапазон
поиска приблизительно в два раза. Следовательно,
общее количество сравнений имеет порядок O (logN).
Задания для самостоятельной работы
1. Реализовать (рекурсивную и
нерекурсивную) схему бинарного поиска с
использованием "барьерной" техники.
2. Ниже по тексту приведены три версии
процедуры бинарного поиска. Какая из них верная?
Исправьте ошибки. Какая из них более эффективная?
Procedure Search;
Var i, j, k: Integer;
Begin
i:=l;j:=N;
Repeat
k:=(i+j) Div 2;
If X<=A[k] Then j:=k-l;
If A[k]<=X Then i:=k+l;
Until i>j
End;
Procedure Search;
Var i, j, k: Integer;
Begin
i:=l;j:=N;
Repeat
k:=(i+j) Div 2;
If X<A[k] then j:=k Else i:=k+l;
Until i>=j
End;
Procedure Search;
Var i, j, k: Integer;
Begin
i:=l;j:=N;
Repeat
k:=(i+j) Div 2;
If A[k]<X Then i:=k Else j:=k;
Until (A[k]=X) Or (i>=j)
End;
3. Решить задачу поиска
числа Х в двухмерном массиве A[1..N, 1..M]
(элементы в строках и столбцах упорядочены) за
время, пропорциональное O(N + M).
Хеширование
Выше рассматривался поиск,
основанный на сравнении значений элементов
массива с некоторым заданным значением
переменной Х (ключом). В конечном итоге
определялся индекс, номер элемента в массиве, где
записано данное значение X. Рассмотрим простую
задачу. Количество различных буквосочетаний
длиной не более 4 символов из 32 букв русского
алфавита чуть больше 10^6. Мы проанализировали
какой-то текст и выписали в соответствующий
массив все встреченные буквосочетания. После
этого на вход нашей простой системы анализа
текста поступает некоторое буквосочетание. Нам
необходимо ответить, встречалось оно ранее или
нет. Очевидно, что каждому буквосочетанию
соответствует некоторый цифровой код. Поэтому
задача сводится к поиску в массиве некоторого
цифрового значения — ключа. Эта задача
рассмотрена ранее (разумеется, можно хранить и
сами буквосочетания). При линейном поиске в
худшем случае для ответа на вопрос "есть или
нет" потребуется 106 сравнений, при бинарном —
порядка 50. Можно ли уменьшить количество
сравнений и уменьшить объем требуемой
оперативной памяти, резервировать не 106, а,
например, 103 элементов памяти? Обозначим
цифровой аналог буквосочетания символом R, 'а
адрес в массиве (таблице) через А. Если будет
найдено преобразование  (R), дающее значение А такое,
что
(R), дающее значение А такое,
что  выполняется достаточно быстро; случаев, когда
выполняется достаточно быстро; случаев, когда  (R1) =
(R1) =  (R2), будет
минимальное количество, то задача поиска
трактуется совсем иначе, чем рассмотрено выше.
Этот способ поиска называется хешированием
(расстановкой ключей, рандомизацией и т.д.). Итак,
ключ преобразуется в адрес, в этом суть метода.
Требование по быстродействию очевидно — это
одна из задач при составлении любого алгоритма,
ибо быстродействие компьютера ограничено.
Второе требование не столь очевидно.
Предположим, что анализируется текст из
специфической страны "Д..", в которой все
слова начинаются с буквы "о" и в качестве
(R2), будет
минимальное количество, то задача поиска
трактуется совсем иначе, чем рассмотрено выше.
Этот способ поиска называется хешированием
(расстановкой ключей, рандомизацией и т.д.). Итак,
ключ преобразуется в адрес, в этом суть метода.
Требование по быстродействию очевидно — это
одна из задач при составлении любого алгоритма,
ибо быстродействие компьютера ограничено.
Второе требование не столь очевидно.
Предположим, что анализируется текст из
специфической страны "Д..", в которой все
слова начинаются с буквы "о" и в качестве  выбран
цифровой аналог первой буквы. В этом случае
получаем одно значение А для всех слов (от
чего уходили, к тому и пришли, но в стране
"Д..." все возможно). Следовательно,
необходимо выбирать такое преобразование
выбран
цифровой аналог первой буквы. В этом случае
получаем одно значение А для всех слов (от
чего уходили, к тому и пришли, но в стране
"Д..." все возможно). Следовательно,
необходимо выбирать такое преобразование  , чтобы
количество совпадений адресов (А) для различных
значений ключей (R) (такие совпадения называют
коллизиями) было минимально. Полностью избежать
коллизий не удается. Для любого преобразования
, чтобы
количество совпадений адресов (А) для различных
значений ключей (R) (такие совпадения называют
коллизиями) было минимально. Полностью избежать
коллизий не удается. Для любого преобразования  (хеш-функции) можно подобрать такие исходные
данные, что рассматриваемый метод поиска
превращается в линейный поиск. Однако цель
построения хеш-функции ясна — как можно более
равномерно "разбрасывать" значения ключей
по таблице адресов (ее размер обозначим через М)
так, чтобы уменьшить количество коллизий. Итак,
реализация метода логически разбивается на две
составляющие:
(хеш-функции) можно подобрать такие исходные
данные, что рассматриваемый метод поиска
превращается в линейный поиск. Однако цель
построения хеш-функции ясна — как можно более
равномерно "разбрасывать" значения ключей
по таблице адресов (ее размер обозначим через М)
так, чтобы уменьшить количество коллизий. Итак,
реализация метода логически разбивается на две
составляющие:
•построение  ;
;
• схема разрешения коллизий.
Коротко рассмотрим их.
Первый вопрос. Так или иначе для значения
ключа R находится цифровой аналог, обозначим его
через t.
Первый способ: в качестве М выбирается
простое число и находится остаток от деления t
на М(t MOD М).
Второй способ: находится значение t2.
Из этого значения "вырезается" q каких-то
разрядов (лучше средних).
Значение q выбирается таким образом,
чтобы 2q было равно М; третий способ: w
разрядов для представления ключа t разбиваются
на части длиной q разрядов. Выполняется,
например, логическое 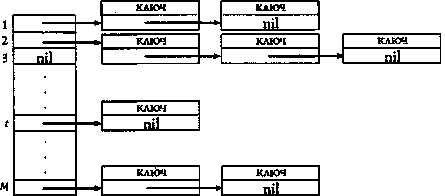 сложение этих частей, и его
результатом является номер элемента в таблице
адресов. Считается (если не заниматься подбором
специальных входных данных), что все эти способы
дают достаточно хорошие в смысле количества
возможных коллизий хеш-функции.
сложение этих частей, и его
результатом является номер элемента в таблице
адресов. Считается (если не заниматься подбором
специальных входных данных), что все эти способы
дают достаточно хорошие в смысле количества
возможных коллизий хеш-функции.
Из известных методов разрешения коллизий
рассмотрим один — "метод цепочек". Его суть
в том, что элементом таблицы является ссылка на
список элементов, имеющих одно значение
хеш-функции. Рисунок справа иллюстрирует этот
метод.
Качество хеш-функции оценивается
средней длиной списков. Рассмотрим следующую
простую задачу. Дано N(1<=N<=15 000) различных
двоичных чисел длины L (1 <= L <= 100), а также Q (1 <= Q
<= 20 000) запросов или двоичных чисел также длины
L.
Требуется определить для каждою запрошенного
числа, встречается оно или нет среди N ранее
определенных чисел. Время решения задачи
ограничено 30 секундами.
Заметим, что сложность "лобового"
решения имеет порядок O(N • L• M), поэтому по
временному ограничению оно вряд ли приемлемо.
Используем метод хеширования. Построим три
различные хеш-функции, а для разрешения коллизий
будем использовать "метод цепочек".
Проверим решения на случайных тестах. Обозначим
цифрой "1" хеш-функцию, использующую деление
на простое число, "2" — возведение в квадрат,
"3" — логические операции с подстроками
фиксированной длины, выделяемые из значения
ключа. Оцениваем минимальную и максимальную
длины списков (Мin, Мах) и время решения (
t ). В таблице приведены результаты нескольких
экспериментов.
| N |
L |
Q |
Хеш-функция |
Min |
Мах |
t |
15000
|
100
|
20000
|
1
2
3 |
14
16
11 |
46
45
50 |
9
27
10.9 |
15000
|
80
|
20000
|
1
2
3 |
13
14
16 |
46
49
48 |
7.3
18
8.9 |
10000
|
50
|
20000
|
1
2
3 |
6
10
0 |
34
34
106 |
4.3
8.7
5.8 |
Рассмотрим реализацию первой
хеш-функции.
Структуры данных.
ConstInputFile='Input.Txt';
OutputFile'Output.TxT';
MaxN=15000;
MaxL=100;
MaxTbl=547; {Размер таблицы.}
Type TNum=Array [0..MaxL Div 8] Of Byte;{Массив для хранения
двоичного числа.
В этом есть определенная сложность,
"затемняющая"
суть решения, но чисто техническая.}
PRec=^TRec;
TRec=Record num:
TNum; next: PRec; End;
Var N, Ln, Q, LnDv8: Integer;
Tbl: Array[0..MaxTbl-1] Of PRec;{Таблица
указателей (ссылок).}
Ряд вспомогательных процедур и
функций.
Procedure ReadNum(Var nw: TNum);{Считываем число.}
Var i: Integer;ch: Char;
Begin
FillChar(nw, SizeOf (nw), 0);
For i:=0 To Ln-1 Do Begin
Read (ch);
nw[i Div 8]:=nw[i Div 8]*2+Ord (ch)-Ord('0');
End;
ReadLn
End;
Procedure AddTRec (Var P: PRec; Const nm: TNum) ;
{Добавить запись в хеш-таблицу. Вставка
осуществляется в начало списка.}
Var smp: PRec;
Begin
If P=nil Then Begin New (P) ;P^ .next:=nil; P^.num:=nrn End
Else Begin New (smp); smp^.next:=P^ .next; smp^.num:=nm;
P^.next:=smp End
End;
Function GetNum(Const p: TNum): Integer;
{Получить хеш-значение для числа. Преобразовать
представление в виде элементов массива в
числовое значение и найти остаток
от деления на простое число, равное размеру
таблицы указателей (ссылок).}
Var i, nw: LongInt
Begin
nw:=0;
For i:=0 To LnDv8 Do nw:=((nw shl 8)+p[i]) Mod MaxTbl;
GetNum:=nw
End;
Procedure Init;
Var i: Integer; nm: TNum;
Begin
FillChar(Tbl, SizeOf (Тbl) , 0) ;
Assign (Input, InputFile); Reset(Input); ReadLn(N, Ln, Q);
LnDv8:=(Ln-1) Div 8;
For i:=1 To N Do Begin
ReadNum (nm) ;
AddTRec(Тbl [GetNum(nm)], nm)
{Добавляем элемент в хеш-таблицу.}
End;
Assign(Output, OutputFile); Rewrite(Output)
End;
Function IfEq(Const a, b: TNum): Boolean;{Сравнение двух ключей.}
Var i: Integer;
Begin
i:=0;
While (i<=LnDv8) And (a [i] =b [i] ) Do Inc(i);
IfEq:=i > (LnDv8)
End;
Основная процедура.
Procedure Solve;
Var i: Integer; nw: TNum; fn: Boolean; uk: PRec;
Begin
For i:=l To Q Do Begin
ReadNum (nw);{Читаем очередное число.}
uk:=Tbl[GetNum(nw)];{Вычисляем адрес в
хеш-таблице.}
fn:=False;
While (uk<>nil) And (Not .fn) Do Begin
{Просматриваем список.}
fn:=IfEq(nw, uk^ .num) ;
{Проверяем, есть ли совпадение?}
uk:=uk^ .next {Переходим к
следующему элементу списка.}
End;
If fn Then WriteLn ('YES') Else WriteLn ('NO') {Выводим
результат.}
End
End;
Основная программа.
Begin Init; Solve; Close(Input); Close(Output) End.
Задания для самостоятельной работы
1. Для реализации второй
хеш-функции (средние биты квадрата числа)
требуется изменить функцию GetNum и добавить одну
константу. Проведите данную модификацию
программы, используя следующую "заготовку".
Const... HwBite=9; МахТbl=1 shl HwBite; {Размер таблицы
указателей 29.}
Function GetNum(Const p: TNum): Integer;{Найти адрес таблицы
указателей для значения ключа р. Программный код
"утяжелен" из-за
необходимости использовать массив для хранения
значения ключа.}
Var i, j, nw: LongInt;clc: Array[0..(MaxL Div 8)*2] Of LongInt;
Begin
FillChar(clc, SizeOf(clc), 0);
For i:=0 To LnDv8 Do {Необходимо перемножить
значения всех байт.}
For j:=0 To LnDv8 Do Begin
Inc(clc[i+j], p[i]*LongInt
(p[j]));Inc(clc[i+j+1], clc[i+j] Div (1 shl 8));
clc[i+j]:=clc[i+j] Mod (1 shl 8)
End;
nw:=0; j:=((HwBite-1) Div 8+1);
For i:=LnDv8-(j Div 2) To LnDv8+(j+l) Div 2-1 Do
nw:=(nw shl 8+clc[i]) Mod MaxTbl;
GetNum:=nw
End;
2. Реализация третьей
хеш-функции также требует изменения только одной
составной части рассмотренной выше логики.
Выполните модификацию программы с
использованием нижеприведенной
"заготовки".
Const ... HwBite=9;MaxTbl=1 shl HwBite;
Function GetScBt (p: Byte): Byte;
Var sc: Integer;
Begin
sc:=0; While p<>0 Do Begin p:=p shr 1; If p Mod 2=1 Then
Inc (sc) End;
GetScBt:=sc Mod 2
End;
Function GetNum(Const p: TNum): Integer;{Получить хеш-значение для
ключа.}
Var i, nw, geth, pp: LongInt;
Begin
nw:=0;
If LnDv8+1<=HwBite Then
For i:=0 To LnDv8 Do nw:=nw*2+GetScBt(p[i])
Else Begin pp:=(LnDv8+l) Div HwBite; geth:=0;
For i:=0 To LnDv8 Do Begin
geth:=geth Xor GetScBt(p[i]) ;
If (i>0)And(((i Mod pp=0) And (i
Div pp<HwBite)) Or (i=LnDv8))
Then Begin nw:=nw*2+geth;
geth:=0 End
End
End;
GetNum:=nw
End;
3. Разработайте свою
методику и, соответственно, программу сравнения
различных хеш-функций. Попробуйте придумать
другие хеш-функции.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() групп по
групп по ![]() элементов в каждой. Выберем максимальный
элемент в каждой группе... Лучше рассмотреть пример попроще.
элементов в каждой. Выберем максимальный
элемент в каждой группе... Лучше рассмотреть пример попроще.![]() ). Метод
интересен с точки зрения проверки техники программирования.
). Метод
интересен с точки зрения проверки техники программирования. ![]()
![]()
![]()



 сложение этих частей, и его
результатом является номер элемента в таблице
адресов. Считается (если не заниматься подбором
специальных входных данных), что все эти способы
дают достаточно хорошие в смысле количества
возможных коллизий хеш-функции.
сложение этих частей, и его
результатом является номер элемента в таблице
адресов. Считается (если не заниматься подбором
специальных входных данных), что все эти способы
дают достаточно хорошие в смысле количества
возможных коллизий хеш-функции.