Вы - -й посетитель этой
странички
Решение задач XIII международной
олимпиады
Е.В. Андреева
Москва
Мобильные телефоны
Предположим,
что в регионе Тампере базовые станции обеспечения мобильной телефонной связи
четвертого поколения действуют следующим образом. Регион поделен на квадраты.
Квадраты образуют матрицу размера SxS,строки и столбцы
которой пронумерованы от 0 до S—1. В каждом
квадрате находится базовая станция. Количество
работающих мобильных телефонов внутри квадрата
может меняться, так как телефоны могут
перемещаться изодного квадрата в другой, и
телефоны могут включаться или выключаться. В
некоторые моменты времени каждая базовая
станция передает головной базовой станции отчет
об изменении количества работающих телефонов и
свои координаты (номер строки и номер столбца
соответственно).
Напишите программу, которая получает эти
отчеты и отвечает на запросы о текущем общем
количестве работающих мобильных телефонов в
некоторой прямоугольной области.
Ввод и вывод
Целочисленные данные вводятся из
стандартного входного потока. Входные данные
кодируются следующим образом. Каждая строка
содержит одну команду. Команда состоит из кода и
набора параметров (целых чисел) в соответствии со
следующей таблицей.
|
Команда |
Параметры |
Значение |
| 0 | S |
Инициализирует матрицу размера SxS нулями. Эта команда выдается только один раз и должна
быть первой командой. |
| 1 | X Y A |
Прибавляет к количеству работающих мобильных телефонов в квадрате (
X, Y) число A.Число A может быть как положительным, так и
отрицательным |
| 2 | L B R T |
Запрашивает текущее суммарное количество работающих мобильных телефонов
в квадратах ( X,
Y), где
L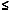 X X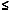 R, B R, B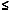 Y Y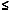 T T |
| 3 | |
Завершает программу. Эта команда выдается только один раз и должна быть
последней |
Программа
отвечает на каждый запрос (команду с кодом 2), записывая целые числа в
стандартный выходной поток.
Значения всегда будут в допустимых пределах, так что нет
необходимости их проверять. В частности, добавление отрицательного числа A не
приведет к уменьшению количества телефонов в квадрате до значения, меньшего
нуля. Индексы в матрице начинаются от 0, например, для матрицы 4 x 4 мы имеем
0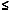 X
X 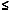 3 и 0
3 и 0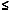 Y
Y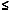 3.
3.
Ваша программа не должна ничего выдавать в
ответ на команды, отличные от команд с кодом 2.
Если поступила команда 2, то ваша программа
должна ответить на запрос, выдав в стандартный
выходной поток строку, содержащую единственное
целое число.
Инструкции для программирования
Далее в примерах целочисленная переменная
last предполагается последней, считанной из
строки, а целочисленная переменная answer содержит
ваш ответ.
Если вы пишете программу на C++ и
используете iostreams, то вам следует
использовать следующие инструкции для чтения из
стандартного входного потока и записи в
стандартный выходной поток:
cin>>last;
cout<<answer<<endl<<flush;
Если вы пишете программу на Cи или С++ и
используете scanf и printf, то вам следует использовать следующие
инструкции для чтения из стандартного входного потока и записи в стандартный
выходной поток:
scanf ("%d",
&last);
printf("%d\n",answer); fflush
(stdout);
Если вы пишете программу на языке Паскаль, то
вам следует использовать следующие инструкции
для чтения из стандартного входного потока и
записи в стандартный выходной поток:
Read(last); ...
Readln;
Writeln(answer);
Пример
Ограничения
|
Размер матрицы |
S x S |
1 x 1
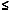 S x S S x S
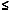 1024 x 1024
1024 x 1024 |
|
В любом квадрате матрицы в каждый момент времени могут находиться
V работающих
телефонов |
V
|
0
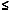 V V
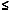 215 - 1
(=32767) 215 - 1
(=32767) |
|
Изменение количества телефонов в квадрате матрицы |
A |
-215
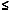 A A
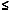 215-1 215-1 |
|
Количество команд во входном потоке |
U |
3
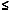 U U
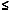 60 002 60 002 |
|
Максимальное суммарное количество телефонов во всей
матрице |
M |
M=230 |
Решение
Решение задачи
проще понять для одномерного случая, то есть для матрицы размерностью 1 x
N. Подсчет количества телефонов сразу на всех интервалах 0 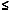 I
I 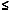 N—1 легко выполняется за O(N) операций, и
все полученные результаты следует сохранить
в таблице. Тогда ответ на запрос о количестве
телефонов в некотором интервале [X, Y]
можно получить следующим образом: S xy
= S y — S x—1 , S y — количество телефонов на интервале [0, Y], а S x—1 —
наинтервале [0, X—1]. То
есть подобный запрос выполняется за O(1) операций.
При изменении количества телефонов в
каком-либо квадрате таблица сумм телефонов
пересчитывается за O(N) действий.
N—1 легко выполняется за O(N) операций, и
все полученные результаты следует сохранить
в таблице. Тогда ответ на запрос о количестве
телефонов в некотором интервале [X, Y]
можно получить следующим образом: S xy
= S y — S x—1 , S y — количество телефонов на интервале [0, Y], а S x—1 —
наинтервале [0, X—1]. То
есть подобный запрос выполняется за O(1) операций.
При изменении количества телефонов в
каком-либо квадрате таблица сумм телефонов
пересчитывается за O(N) действий.
Однако если вспомогательные суммы
хранить в виде специального дерева, то обновлять
их можно за O(logN) операций. Хранить же такое, хотя и
не бинарное, дерево можно с помощью одномерного массива
из N элементов,индексы которого удобно обозначать
от 1 до N. I-й элемент такого массива содержит
сумму элементов исходного массива на
интервале [I—2 k , I—1], где за k мы всегда будем
обозначать число нулей в конце двоичного представления
индекса элемента вспомогательного
массива. Например, в четвертом элементе
вспомогательного массива хранится
сумма элементов с 0-го по 3-й исходного
массива, так как 4 = 100 2 , то есть два нуля в конце двоичного
представления, и I — 2 k = 4 — 2 2 = 0, а в
шестом элементе — сумма только четвертого и
пятого элементов, так как 6 = 110 2 и I — 2 k = 6
— 2 1 = 4. Обновляется
вспомогательный массив так. Если какой-то
элемент исходного массива изменился, тотакже
меняется и соответствующий элемент
вспомогательного массива. Индекс следующего
элемента вспомогательного массива, который тоже
следует изменить, вычисляется следующим образом:
к индексу текущего элемента прибавляется 2 k .Например, если на 3
увеличилось количество телефонов в квадрате 2 (он
третий по счету), то сначала на 3 увеличивается 3-й
элемент массива, затем на три же 4-й (3 = 11 2 , k = 0, 3 + 2 0
= 4), затем 8-й (4 = 100 2
, k = 2, 4 + 2 2 = 8) и т.д. Так как значение k на
каждом шаге увеличивается, обновление
массива производится за O(logN) действий.Сумму же элементов
на любом интервале [ 0, I—1] c помощью
построенного дерева можно подсчитать так.
Начинаем с элемента вспомогательного массива с
индексом I. Следующий элемент дерева,
который следует включить всумму, вычисляется как
I—2 k и т.д., пока
не дойдем до 0 (нулевого элемента у нас в дереве
нет).
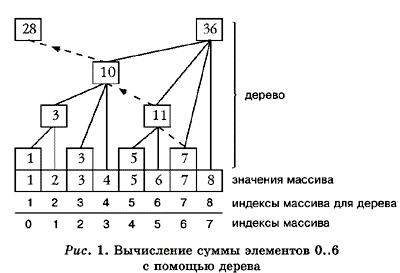 Например, сумма элементов на
интервале [0, 6] вычисляется как сумма элементов
дерева с индексами 7, 6 и 4 (7 = 111 2 , k = 0,7 — 2 0, = 6; 6
= 110 2 , k = 1, 6 — 2 1 = 4; 4 = 100 2
, k = 2, 4 — 2 2 = 0, см. также рис.1).
Например, сумма элементов на
интервале [0, 6] вычисляется как сумма элементов
дерева с индексами 7, 6 и 4 (7 = 111 2 , k = 0,7 — 2 0, = 6; 6
= 110 2 , k = 1, 6 — 2 1 = 4; 4 = 100 2
, k = 2, 4 — 2 2 = 0, см. также рис.1).
Такая операция
производится также за O(logN) действий. А
запрос относительно количества телефонов на любом
интервале, как уже было показано выше, выполняется
за две такие операции. Следовательно, любая
команда из условия задачи для
одномерного случая выполнима не более чем
за O(logN) действий. Заметим также, чтомассив со значениями
телефонов в каждом квадрате можно не
хранить. Достаточно иметь массив для хранения
описанного дерева сумм.
Решение для одномерного
случая может быть распространено на двухмерный случай следующим образом. Нам
потребуется построить дерево деревьев, имеющих структуру, аналогичную описанной
выше, и хранить его в квадратном массиве, по размеру и индексам совпадающем с
исходным, исходный же массив хранить не будем. Тогда элемент [X—1, Y—1] такой
древообразной структуры содержит сумму элементов в области, размер которой
определяется количеством конечных нулей в двоичном представлении X и Y. Такая
структура позволяет подсчитывать сумму телефонов в прямоугольнике [0, X] x
[0, Y] за O ((logN) 2) действий (см. рис. 2).
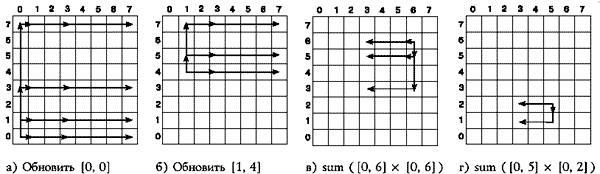
рис.2
Запрос о количестве телефонов в
любой прямоугольной области можно выполнить за 4
подобных операции:
sum ([L, R] x
[B, T]) = sum ([0, R] x [0, T]) — sum ([0, L—1] x [0, T]) — sum ([0,
R] x [0,
B—1]) +
+ sum([0, L—1] x
[0, B—1]).
Приведем программу решения этой задачи.
const
max_size=1023;< BR>var
table: array
[0..max_size,0..max_size] of longint;
N,size,cmd, a1, a2, a3, a4: longint;
function low_bit (x: longint): longint; {Для x получает
соответствующие 2^k}
begin
low_bit:=x and (x xor
(x-1))< BR> end;
procedure update
(x,y,amount:longint); {Обновляет матрицу}
var ix:longint;
begin
inc (x); inc (y);
while y <= size do< BR> begin
ix :=
x;< BR> while ix <=
size do< BR>
begin
inc ( table [ix-1,y-1], amount );
inc ( ix,low_bit ( ix ) )
end;
inc ( y,low_bit (
y ) )
end
end;
function sum
(x,y:longint): longint; {Находит сумму элементов в [0,X] x
[0,Y]}
var res,
ix, iy: longint;
begin
res :=
0;< BR> iy := y +
1;< BR> while iy > 0
do
begin
ix := x + 1;<
BR>
while ix > 0 do
begin
inc ( res, table [ix -
1,iy - 1] );
dec ( ix, low_bit ( ix ) )
end;
dec ( iy ,
low_bit ( iy ) )
end;
sum :=
res< BR> end;
BEGIN
repeat
read ( cmd
);
case cmd
of
0:
begin
read ( n );
size := 1;<
BR>
while size < n do size := size shl
1<
BR>
end;
1:begin
read ( a1, a2, a3 );
update ( a1, a2, a3 )
end;
2:begin
read ( a1, a2, a3, a4 );
writeln ( sum ( a3, a4 )- sum ( a1-1, a2 ) - sum ( a1, a2-1 ) + sum ( a1-1, a2-1
) )
end
end
until cmd = 3< BR > END.
Продолжение следует
 Например, сумма элементов на
интервале [0, 6] вычисляется как сумма элементов
дерева с индексами 7, 6 и 4 (7 = 111 2 , k = 0,7 — 2 0, = 6; 6
= 110 2 , k = 1, 6 — 2 1 = 4; 4 = 100 2
, k = 2, 4 — 2 2 = 0, см. также рис.1).
Например, сумма элементов на
интервале [0, 6] вычисляется как сумма элементов
дерева с индексами 7, 6 и 4 (7 = 111 2 , k = 0,7 — 2 0, = 6; 6
= 110 2 , k = 1, 6 — 2 1 = 4; 4 = 100 2
, k = 2, 4 — 2 2 = 0, см. также рис.1).
