Вы - -й посетитель этой странички 

План занятия:
    • обсуждение оператора;
    • эксперименты с программами определения простота числа и нахождения наибольшего общего делителя двух чисел с помощью алгоритма Евклида;
    • выполнение самостоятельной работы.

    Оператор Repeat (повторять) ... Until (до тех пор, пока не) содержит логическое выражение (после Until), которое управляет повторением последовательности операторов, записанных между Repeat и Until. Повторение продолжается до тех пор, пока логическое выражение не примет значение True. Последовательность операторов выполняется по меньшей мере один раз, ибо логическое выражение вычисляется после выполнения данной последовательности (поэтому данный цикл называют циклом с постусловием).

    Repeat
        <оператор₁>;
         <оператор₂>;
        ...

        <оператор_n>;
    Until <логическое выражение>

    При использовании оператора Repeat ... Until необходимо учитывать следующее:
    • последобательность операторов должна содержать хотя бы один оператор, влияющий на значение логического выражения;
    • для того чтобы цикл завершился, логическое выражение рано или поздно должно принять значение True. 
    Приведем простейший пример бесконечною цикла: Repeat ... Until False;

    1. Натуральное число р называется простым, если оно делится только на 1 и на себя. По соглашению 1 не считают простым числом. Начало последовательности простых чисел имеет вид: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...
    В программе Му8_1 определяется, является ли данное число простым. Мы ищем делители числа п в интервале от 2 до п div 2, хотя можно было бы ограничиться интервалом от 2 до целой части Ön (почему?).

Program My8_l;
    Var i, n : LongInt;
    Begin
        WriteLn ('Введите натуральное число');
        ReadLn (n);
        i : = l;
        Repeat
           Inc(i)
        Until (i > n div 2) Or (n mod i = 0);
        If i > n div 2 Then Writeln (' Число ',n, ' простое '}
        Else WriteLn ('Число ' ,i, ' - первый делитель числа' ,n, ', больший 1');
        ReadLn
    End.
    Эту задачу можно решить и с использованием оператора While (см. предыдущее занятие). Сделайте это. Затем измените программу так, чтобы в ней осуществлялся вывод всех делителей числа п.

    Подсказка. Логическое выражение в операторе Repeat ... Until упростится, в нем останется только условие i > n div 2, а в теле цикла появится оператор If n mod i = 0 Then WriteLn (..., i).

    Основная теорема арифметики. Всякое натуральное число п > 1 разлагается на произведения простых чисел. Это разложение однозначно с точностью до порядка записи простых чисел в произведении.

    Выберите интервал чисел (не очень большой, например, от 101 до 120) и, используя модифицированную программу Му1_8, найдите разложения этих чисел на произведения простых. Ваши записи должны иметь вид:

n = p₁^a1 • p₂^a2 • ... • p_q^aq

— где (a_i >= 0), р_i — простые числа, например, 168= 2³ • 3¹ • 5⁰ • 7¹.
    2. Наибольший общий делитель (НОД) двух целых чисел а и b — это наибольшее целое число, которое делит нацело оба числа. Далее мы будем рассматривать лишь неотрицательные числа, но это не влияет на общность рассуждений. Для нахождения НОД чисел а и b можно представить оба числа в виде:

a = p₁^a1 • p₂^a2 • ... • p_q^aq и b = p₁^b1 • p₂^b2 • ... • p_r^br

— а затем найти НОД (а, b) в виде:

 p₁^min(a1,b1) • p₂^min(a2,b2) • ... • p_m^min(am,bm).

Отложим исследование этого метода нахождения НОД и рассмотрим другой способ, который называется алгоритмом Евклида. Пусть а и b одновременно не равные нулю целые неотрицательные числа и a >= b. Если b = 0, то НОД (а, b) = a, а если b 0, то для чисел а, b и r, где r — остаток от деления а на b, выполняется равенство НОД (а, b) = НОД (b, r). Действительно, r = a mod b = а — (a div b) • b. Если какое-то число делит нацело и а, и b, то из приведенного равенства следует, что оно делит нацело и число r.

Например, пусть а = 48, а b = 18. Приведем ручную трассировку алгоритма Евклида.

    Таким образом, НОД(48, 18) = б.
    Программная реализация алгоритма Евклида с использованием оператора Repeat ... Until имеет вид:

Program My8_2;
    Var a, b: LongInt;
    Begin
        WriteLn ('Введите два числа');
        ReadLn (a, b) ;
        Repeat
          If a>b Then a:=a mod b Else b:=b mod a
        Until (a=0) or (b=0) ;
        WriteLn ('НОД=', а+b) ;
        ReadLn
End.

    Измените программу так, чтобы вместо оператора Repeat . . . Until использовался оператор While. Какое ограничение в этом случае можно убрать?
    Элементы е_i последовательности
    е₁ = 1 + 1 = 2,
    е₂ = 2 + 1 = 3,
    е₃ = 2 • 3 + 1 = 7,
    е₄ = 2 • 3 • 7 + 1 = 43,
    е₅ = 2 • 3 • 7 • 43 + 1 = 1807,
    е₆ = 2 • 3 • 7 • 1807 + 1 = 3263443,
    е₇ = 2 • 3 • 7 • 1807 • 3263443 + 1 = 547 • 607 • 1033 • 31051 и т.д.
называют числами Евклида. По первым четырем числам кажется, что числа Евклида простые. Однако это не так, уже е₅ является составным — 1807 = 13 • 139. Известно, что евклидовы числа взаимно простые — НОД(e_i, е_j) = 1 при i j. Проверьте этот факт с помощью программы Му8_2 для первых шести чисел Евклида. Используя программу Му8_1, покажите, что число е₆ простое.
    3. В теории чисел доказывается следующая теорема. Если а и b одновременно не равны нулю, то существуют целые числа х и у, такие, что НОД(а, b) = а • х + b • у. Теорема не утверждает, что х и у определены однозначно, в ней лишь говорится о том, что НОД(а, b) может быть выражен в таком виде. Например, 
    6 = НОД (12, 30)= 12 • 3 + 30 • -1.

    Рассмотрим последовательность:
    a₀ = a • x₀ + b • y₀, где x₀ = 1, y₀ = 0;
    a₁ = a • x₁ + b • y₁, где x₁ = 0, y₁ = 1;
    a₂ = a₀ - a₁• q₁, где q₁ = a₀ div a₁;

подставляя значения a₀ и a₁ получаем:
    a₂ = a • x₀ + b • y₀ - (a • x₁ + b • y₁) • q₁ = a • (x₀ - x₁ • q₁) + b • ( y₀ -  y₁ • q₁) = a • x₂ + b • y₂
   a₃ = a₁ - a₂ • q₂, где q₂ = a₁ div a₂

подставляя значения a₁ и a₂ получаем:
   a₃ = a • x₁ + b • y₁ - (a • x₂ + b • y₂) • q₂ = a • (x₁ - x₂ • q₂) + b •(y₁ - y₂ • q₂) = a • x₃ + b • y₃;
    ...
   a_i = a_i-2 - a_i-1 • q_i-1, где q_i-1 = a_i-2 div a_i-1,
    a_i = a • x_i-2 + b • y_i-2 - (a • x_i-1 + b • y_i-1) • q_i-1 = a • x_i + b • y_i;
    ...
   0 = a_k-1 - a_k • q_k, где q_k = a_k-1 div a_k, ... 0 = a • x_k+1 + b • y_k+1.

    Таким образом, значения q_i, a_i, x_i , y_i, определяются рекуррентными соотношениями:
   q_i-1 = a_i-2 div a_i-1;
   a_i = q_i-2 - a_i-1 • q_i-1;
    x_i = x_i-2 - x_i-1 • q_i-1;
   y_i = y_i-2 - y_i-1 • q_i-1;

    Рассмотрим данный процесс на примере чисел а = 48 и b= 18.

     Итак, d = НОД(48,18) = 6 и 6 = 48 • (-1)+18 • 3.
    Описанный алгоритм реализован в программе My 8_3.

Program Му8__3;
    Var a, b, a0, a1, x0, x1, y0, y1, q, t : Integer;
    Begin
    WriteLn('Введите два числа, первое должно быть больше второго ');
    ReadLn(а, b) ;
    a0:=a; a1:=b; x0:=1; x1:=0; у0:=0; у1:=1;
    Repeat
        q:=a0 div a1;
        t:=a0; a0:=a1; a1:=t-a1*q;
        t:=x0; x0:=x1; x1:=t-x1*q;
        t:=y0; y0:=y1; y1:=t-y1*q
    Until a1=0;
    WriteLn (a0, '=',а, '*(', x0,') + ',b,' * (', y0, ') ');
    ReadLn
End.

    Сравните результаты, полученные с помощью ручной трассировки, с результатами работы программы при тех же исходных данных.

    1. Числа вида 2^P — 1, где р — простое число, называются числами Мерсенна. Являются ли числа Мерсенна при значениях р 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 простыми? Для ответа на этот вопрос напишите соответствующую программу. Программа должна состоять из двух частей: в первой вычисляется число Мерсенна для значения р (р вводится с клавиатуры), во второй проверяется, является ли оно простым.
    2. Линейные уравнения от двух переменных (линейные диофантовые уравнения), т.е. уравнения вида:
а•х + b•у = с, — в которых а и b не равны нулю одновременно, имеют целые решения тогда и только тогда, когда d = НОД(а, b) делит нацело число с. Причем, если x₀, y₀ — некоторое (частное) решение, то все решения имеют вид:
    х = x₀ — п • (b div d),
    у = y₀ + n • (а div d) для всех п.
    Пример: 12 • х — 30 • y = 84, НОД(12, —30) = 6, 84 делится нацело на 6. Уравнение разрешимо. Одним из его решений является (х, у) = (2, —2). Все остальные решения имеют вид: х= 2+ 5 • n, у = —2+ 2 • n.
    Даны целые числа а, b, с. Написать программу определения разрешимости соответствующего диофантового уравнения и, если оно разрешимо, поиска частного решения.
    3. Пусть а и b — ненулевые целые числа. Целое число т > 0 называется наименьшим общим кратным (НОК) чисел а и b, если т делится и на а, и на b нацело, а также любое с, которое делится нацело и на a, и на b, делится нацело и на т.
    Если a и b — ненулевые числа, то их наименьшее общее кратное существует и справедливо равенство НОК(а, b) = |а • b| div НОД(a, b). Написать программу нахождения НОК двух ненулевых чисел.
    4. Числа Фибоначчи (f_n) определяются формулами: f₀ = f₁ = 1; f_n = f_n-1 + f_n-2 при n >= 2. Начало последовательности Фибоначчи имеет вид: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,... Составить программы:
    • определения номера последнего числа Фибоначчи, которое входит в диапазон типа Integer (LongInt);
    • вычисления s — суммы первых чисел Фибоначчи, таких, что значение s не превышает диапазона типа Integer (LongInt).
    5. Совершенным называется число, равное сумме всех своих делителей, меньших, чем оно само. Например:
6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14. Составьте программу, проверяющую, является ли заданное натуральное число совершенным.
    Примечание. Евклидом доказано, что каждое число вида 2^p-1• (2^P — 1) является совершенным, если 2^p — 1 — простое число. Л.Эйлер доказал, что все четные совершенные числа находятся по формуле Евклида, а относительно нечетных совершенных чисел ничего неизвестно до сих пор.
    6. Автоморфным называется число, равное последним цифрам своего квадрата. Например: 5² = 25, 25² = 625. Очевидно, что автоморфные числа должны оканчиваться либо на 1, либо на 5, либо на 6. Составьте программу нахождения автоморфных чисел (с учетом приведенного факта), не превышающих значения 999.
    Примечание. Не забывайте о диапазонах переменных целого типа, 999² =  998001.
    7. Кубические автоморфные числа равны последним цифрам своих кубов. Например: б³ = 216. Верно ли, что и такие числа должны оканчиваться либо на 1, либо на 5, либо на б? Составьте программу нахождения двузначных и трехзначных кубических автоморфных чисел.

    1. Продолжим наше знакомство с основными понятиями технологий программирования. Познакомимся с понятием модели жизненного цикла программы. В настоящее время понятие жизненного цикла программы является одним из базовых понятий в технологии программирования. Жизненный цикл программы начинается с момента принятия решения о необходимости ее создания и заканчивается в момент полного изъятия программы из эксплуатации. Основным нормативным документом, регламентирующим жизненный цикл программы, является международный стандарт ISO / IEC 12207 (ISO — International Organisation of Standardisation — Международная организация по стандартизации, IEC — International Electrotechnical Commission — Международная комиссия по электротехнике). Он определяет структуру жизненного цикла, которая базируется на трех группах процессов:
    • основные процессы (приобретение, поставка, разработка, эксплуатация, сопровождение);
    • вспомогательные процессы, обеспечивающие выполнение основных процессов (документирование, управление конфигурацией, обеспечение качества, верификация, аттестация, оценка, аудит);
    • организационные процессы (управление проектами, создание инфраструктуры проекта, обучение). К настоящему времени известны две основные модели жизненного цикла:
    • каскадная — см. рис. 1—2;
    • спиральная — см. рис. 3.

Анализ
	Проектирование
		Реализация
			Внедрение
				Сопровождение

Рис. 1

Рис. 2

    Каскадный подход хорошо зарекомендовал себя при построении программ, к которым в самом начале разработки можно достаточно точно и полно сформулировать все требования. Пример — расчетные задачи. В случае неточного изложения требований или их изменения получается программа, не отвечающая потребностям пользователя, заказчика, поэтому реальный процесс разработки представлен на рис. 2.

    Для преодоления недостатков каскадной схемы была предложена спиральная модель жизненного цикла программы (рис. 3). Каждый виток спирали соответствует созданию очередной версии программы. При этом уточняются цели и требования, определяется качество и планируются работы по созданию следующей версии. Таким образом, последовательно конкретизируются детали программы и выбирается окончательная версия, которая доводится до реализации. Сходящий вид спирали подчеркивает "размытость" первоначальных требований и их последующее уточнение.
    2. Ошибки в программах принято разделять на синтаксические, семантические и логические. С первыми мы встречались на предыдущих занятиях. Они достаточно просто устраняются и говорят о несоответствии текста программы правилам языка. Вторые возникают на стадии выполнения программы. Например, деление на ноль не устраняется на стадии компиляции, а приводит к ошибке на стадии выполнения, ибо зависит от конкретного значения переменной. Третий тип ошибок самый сложный в обнаружении. Программа работает так, как написана, но не так, как предполагалось. Такие ошибки часто сложно обнаружить. В системе Турбо Паскаль имеется достаточно мощный отладчик, позволяющий находить ошибки третьего типа в программах. Он работает с исходным текстом программы, позволяет выполнять программу по шагам и отслеживать изменение переменных программы в процессе работы последней.
    Перечислим основные команды отладчика и соответствующие им клавиши, позволяющие выполнять программу по шагам и отслеживать значения переменных. Шагом при отладке является строка программы. Так, если в строке исходного текста программы записано несколько операторов, то они будут выполнены за один шаг.

План занятия
    • обсуждение конструкции;
    • эксперименты с программами (с использованием отладчика системы программирования) вычисления выражения 1^k + 2^k + ... + n^k ; нахождения цифрового корня числа; решения старинной задачи о быках, коровах и телятах; нахождения натуральных чисел, удовлетворяющих определенному условию; сведение чисел, кратных 3, к числу 153;
    • выполнение самостоятельной работы.
    Для решения задачи достаточно часто требуется использовать две и более циклические конструкции, одна из которых расположена внутри другой (других). Такие конструкции называют вложенными циклами. Какие именно циклы при этом используются, роли не играет, они могут быть организованы посредством любых рассмотренных ранее операторов (For, While, Repeat ... Until).

    1. Даны натуральные числа n и k. Составить программу вычисления выражения 1 ^k + 2 ^k + ... + n ^k .
    Для вычисления указанной суммы целесообразноиспользовать оператор For с управляющей переменной i, изменяющейся от 1 до n. В теле цикла вычисляется очередное значение y = i^k и накапливается искомая сумма s = s + y.

Program My9_1;
    Var n, k, y, i, s, j : Integer;
    Begin
        WriteLn ('Введите n и k ');
         ReadLn (n, k);
         s:=0;
         For i:=1 To n Do Begin
             y:=1;
             For j:=1 To k Do y:=y*i;
             s:=s+y
         End;
        WriteLn ('Сумма: ',s)
    End.

    А сейчас попробуем работать с отладчиком системы программирования. Вспомните материал для чтения
предыдущего занятия, пункт 4.

    • Выполните команду Debug/Watch. Появится окно Watches.
    • Используя клавишу <Insert> (при этом открывается окно Add Watch), введите переменные программы (n, k, s, i, j, y).
    • Измените положение и размер окна Watches на экране. Оно должно находиться в правом верхнем углу и быть таким, чтобы все введенные переменные были видны. С этой целью выполните команду Window/Size/Move ( <Ctrl> + <F5> ) и используйте клавиши <Shift> + <¬> ,<®> , <¯>, <> для изменения размеров окна и клавиши <¬> ,<®> , <¯>, <> для его перемещения.
    • Выполните команду Run/Step over (<F8>). При этом строка с оператором Begin выделяется другим цветом. При нажатии на <F8> управление передается на следующую строку (эта строка становится выделенной).
     • Выполните программу в пошаговом режиме (посредством последовательных нажатий на клавишу <F8>), отслеживая изменение значений переменных в окне Watches. При выполнении оператора ReadLn (n,k) введите, например, значения 4 и 2, для того чтобы количество повторений в операторах For было не очень большим.

Продолжим изучение отладчика.
    • Установите курсор на строку программы с оператором s:=s+y. Выполните команду Debug/Add Breakpoint (<Ctrl> + <F8>). Строка будет выделена другим цветом. Таким образом, в программе создается точка останова.
    • Запустите программу (<Ctrl> + <F9>). При достижении точки останова выполнение программы приостанавливается.
    • Выполните один шаг программы (нажмите клавишу <F8>).
    • Выполните команду Debug/Evaluate... В строке Expression окна Evaluate and Modify наберите имя переменной s. В строке Result окна мы видим значение переменной s, оно равно 1.
    • Продолжите работу с программой по описанной схеме. На следующем шаге цикла значение переменной s будет равно 5.

    Рекомендуется максимально использовать отладчик системы программирования при выполнении заданий этого и следующих занятий.

    Измените программу так, чтобы в ней вычислялась сумма 1¹ + 2² + ... + nⁿ .

    Решите следующую задачу. Пусть значение k зафиксировано, например, равно 5. Требуется определить

значение n, при котором диапазона целого типа данных Integer окажется недостаточно для хранения суммы.

    2. Сложим все цифры какого-либо числа. Получим новое число, равное сумме всех цифр исходного числа. Продолжим этот процесс до тех пор, пока не получим однозначное число (цифру). Оно называется цифровым корнем исходного числа. Например, цифровой корень числа 34 697 равен 2 (3 + 4 + 6 + 9 + 7 = 29; 2 + 9 = 11; 1 + 1 = 2). Составьте программу нахождения цифрового корня натурального числа.

Program My9_2;
    Var n, k, s : LongInt;
    Begin
        WriteLn ('Введите число');ReadLn(n);
         s:=n;
           While s>9 Do Begin
                k:=s; s:=0;
            Repeat
                 s:=s + k mod 10;
                 k:=k div 10
               Until k=0
           End;
         WriteLn ('Цифровой корень числа ',n,' равен ',s)
      End.

    3. Старинная задача. Сколько можно купить быков, коров и телят, если бык стоит 10 рублей, корова —  
5 рублей, теленок — полтинник (0,5 рубля), при условии, что на 100 рублей надо купить 100 голов скота.
    Решение. Обозначим через b — количество быков, k — количество коров, t — количество телят. После этого можно записать два уравнения:
        10b + 5k + 0,5t = 100 и b + k + t = 100.
Преобразуем их:
         20b + 10k + t = 200 и b + k + t = 100.
    На 100 рублей можно купить:
    · не более 10 быков, т.е. 0 £ b £ 10,
    · не более 20 коров, т.е. 0 £ k £ 20,
    · не более 200 телят, т.е. 0 £ t £ 200.
    Таким образом, получаем:

Program My9_3;
    Var b, k, t: Integer;
    Begin
        For b:=0 To 10 Do
         For k:=0 To 20 Do
           For t:=0 To 200 Do
             If (20*b+10*k+t=200) and (b+k+t=100) Then
              WriteLn ('быков ',b,' коров ',k,'телят ',t)
End.

Сколько раз будет проверяться условие в данной программе (сколько раз будет выполняться оператор If)?
Переменная b принимает 11 различных значений (от 0 до 10), для каждого значения переменной b переменная k изменяется от 0 до 20, а для каждого значения переменной k переменная t изменяется от 0 до 200. Таким образом, условие будет проверяться 11 • 21 • 201 = 46 431 раз. Но если известно количество быков и коров, то количество телят можно вычислить по формуле t = 100 — (b + k) и цикл по переменной t можно исключить.

Program My9_3m;
    Var b, k, t: Integer;
    Begin
         For b:=0 To 10 Do
             For k:=0 To 20 Do Begin
                 t:=100-(b+k);
             If (20*b+10*k+t=200) Then WriteLn ('быков', b,' коров ',k,' телят ',t)
             End
    End.

    В этой программе условие проверяется 11•21 = 231 раз. Попробуйте еще уменьшить количество проверок.

    4. Написать программу, которая находит все четырехзначные числа abcd (a, b, c, d — цифры числа, причем все они различны), для которых выполняется условие: ab — cd = a + b + c + d. Другими словами, разность чисел, составленных из старших цифр числа и из младших, должна быть равна сумме цифр числа.
    Эту задачу можно решать разными способами. Например, можно перебирать все четырехзначные числа и проверять выполнение условия. Попробуем сократить перебор: из равенства
    10 • a + b — (10 • c + d) = a + b + c + d
получаем
                                 9•(a — c) = 2•(c + d)
или                    (a — c)/(c + d) = 2/9,
                                a = c + 2, d = 9 — c и 0 £ c £ 7.

Program My9_4;
    Var a, b, c, d:Integer;
    Begin
         For c:=0 To 7 Do Begin
             a:=c+2; d:=9-c;
             For b:=0 To 9 Do
                 If (b<>c)and(b<>a)and(b<>d) Then WriteLn (a,b,c,d)
         End
    End.

    5. Дано натуральное число, кратное 3. Найдем сумму кубов цифр данного числа. Получим новое число. Применим к нему такое же преобразование и т.д. Оказывается, что любая такая последовательность чисел сходится к числу 153.

Program My9_5;
    Var n, m, t, s, q:LongInt;
    Begin
         WriteLn ('Введите число, оно умножается на 3, далее для полученного числа строится последовательность');
        ReadLn(n);
         m:=3*n;Write(m,' ');
         Repeat
             s:=0;t:=m;
             While m>0 Do Begin
             q:=m mod 10;
                 s:=s+q*q*q;
                 m:=m div 10
             End;
          m:=s;
          Write (m,' ')
         Until m=t;
        ReadLn
    End.

    1. Что будет напечатано в результате выполнения следующего фрагмента программы при n = 6?

a:=1; b:=1;
For i:=0 To n Do Begin
    For j:=1 To b Do Write ('*');
    WriteLn;
    c:=a+b; a:=b; b:=c
End;

    Какая задача решается в этом фрагменте программы?

    2. Что будет напечатано в результате выполнения следующего фрагмента программы при а = 13 305?

b:=0;
While a<>0 Do Begin
    b:=b*10+a mod 10
    a:=a div 10;
End;
Write (b);

    Какая задача решается в этом фрагменте программы?

    3. Дано натуральное число q. Требуется написать программу для нахождения всех прямоугольников, площадь которых равна q и стороны выражены натуральными числами.

    4. Составить программу для иллюстрации делимости чисел от 1 до n. В каждой строке надо печатать число и столько плюсов, сколько делителей у этого числа. Например, если n = 4, то на экране должно быть напечатано:
                             1+
                             2++
                            3++
                            4+++

    5. Дано натуральное число n. Требуется выяснить, можно ли представить его в виде суммы квадратов трех натуральных чисел? Если можно, то:
    · указать тройку x, y, z таких натуральных чисел, что x² + y² + z² = n;
   · указать все тройки x, y, z таких натуральных чисел, что x² + y² + z² = n.

    6. Найти натуральное число от 1 до 10 000 с максимальной суммой делителей.

    7. Даны натуральные числа a, b (a < b). Получить все простые числа p, удовлетворяющие неравенствам:
a £ p £ b.

    8. Даны натуральные числа n, m. Получить все натуральные числа, меньшие n, квадрат суммы цифр которых равен m.

    9. Даны натуральные числа n и m. Найти все пары дружественных чисел, лежащих в диапазоне от n до m. Два числа называются дружественными, если каждое из них равно сумме всех делителей другого (само число в указанную сумму не входит).

    10. Переставить цифры данного натурального числа таким образом, чтобы образовалось наименьшее число, записанное этими же цифрами.

    11. Составить программу, печатающую k-ю цифру последовательности:
    · 12345678910..., в которой выписаны подряд все натуральные числа;
    · 14916253649..., в которой выписаны подряд квадраты всех натуральных чисел;
    · 1123581321..., в которой выписаны подряд все числа Фибоначчи.

    12. Составить программу возведения заданного числа в третью степень, используя следующую закономерность:

                            1³ = 1
                             2³ = 3 + 5
                             3³ = 7 + 9 + 11
                             4³ = 13 + 15 + 17 + 19
                             5³ = 21 + 23 + 25 + 27 + 29

    13. Составить программу для нахождения всех натуральных чисел n, m, k из интервала [1, 10], удовлетворяющих соотношению n² + m² = k² .
    Примечание. Решения, которые получаются перестановкой n и m, считать совпадающими.

    14. Написать фрагмент программы для решения каждой из указанных ниже задач и обосновать, почему вами был выбран тот или иной оператор цикла:
    · вычислить факториал некоторого числа p;
    · задано число p, определить, является ли оно факториалом некоторого числа, если “да”, то найти это число;
    · определить, является ли заданное число степенью числа 3;
    · вычислить 1! + 2! + 3! + ... + n!;
    · вычислить xⁿ , где n — целое положительное число;
    · вычислить значения x¹ , x² , x³ , ..., xⁿ .

    15. Дано трехзначное число. Найти все трехзначные числа, удовлетворяющие каждому из условий:
    · состоящих из тех же цифр, что и исходное число;
    · равные среднему арифметическому всех трехзначных чисел (включая данное), состоящих из тех же цифр.

    16. Стороны прямоугольника заданы натуральными числами M и N. Составить программу, которая будет находить, на сколько квадратов, стороны которых выражены натуральными числами, можно разрезать данный прямоугольник, если от него каждый раз отрезается квадрат максимально возможной площади.

    17. Даны натуральные числа N и p. Получить все натуральные числа, меньшие N и взаимно простые с p.

    18. Даны целые числа p и q. Получить все делители числа q, взаимно простые с p.

    19. Сумма квадратов длин катетов a и b прямоугольного треугольника равна квадрату длины гипотенузы с: a² + b² = c² . Тройка натуральных чисел, удовлетворяющих этому равенству, называется пифагоровой. Составить программу нахождения пифагоровых троек, используя следующие формулы:
                             a = u•v; b = (u•u — v•v) div 2,
                             c = (u•u + v•v) div 2,
— где u и v — взаимно простые нечетные натуральные числа и u > v.

    20. Найти наименьшее натуральное число N, представимое двумя различными способами в виде суммы кубов двух натуральных чисел x и y (x ³ y).

    21. Даны натуральные числа m, n₁ , n₂ , ..., n_m (m ³ 2). Вычислить НОД (n₁ , n₂ , ..., n_m ), воспользовавшись соотношением НОД (n₁ , n₂ , ..., n_m ) = НОД (НОД (n₁ , n₂ , ..., n_m—1 ),  n_m ) и алгоритмом Евклида.

    22. Найти все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7 (дробь задается двумя натуральными числами — числителем и знаменателем).

Заключение

    В первой части учебника рассмотрены основные операторы языка программирования Турбо Паскаль. Разобраны 23 задачи и 116 предложено для самостоятельной работы. Предметной областью для выбора задач является “Теория чисел”. Знание этого раздела математики — необходимая компонента математической культуры специалиста по информатике.
    Дополнительно можно порекомендовать следующие книги.

    1. О системах счисления и представлении чисел в памяти компьютера написано прекрасное учебное пособие (Андреева Е., Фалина И. Информатика: Системы счисления и компьютерная арифметика. М.: Лаборатория базовых знаний, 1999, 256 с.).

    2. О математической логике можно почитать во второй главе учебно-справочного издания А.И. Гусевой (Гусева А.И. Учимся информатике: задачи и методы решения. М.: “Диалог-МИФИ”, 1998, 320 с.).

    3. По теории чисел трудно найти что-либо лучше классической книги И.М. Виноградова. Но читать ее достаточно сложно, особенно если вы не очень дружите с математикой (Виноградов И.М. Основы теории чисел. М.: Наука, 1972, 167 с.).

    4. О профессии программиста с большим юмором написана книга А.Н. Венца. В ней вы найдете и экскурсы в историю программирования (Венц А. Профессия — программист. Ростов-на-Дону: Изд-во “Феникс”, 1999, 384 с.).

    5. О технологиях программирования лучше всего читать в классической книге Г.Буча, настольной книге любого программиста (Буч Г. Объектно-ориентированное проектирование с примерами применения: Пер. с англ. М.: Конкорд, 1992, 519 с.).

    6. Много полезных примеров из истории программирования можно найти в уникальной книге компьютерного провидца (так его называют) Д.Васкевича (Васкевич Д. Стратегия клиент/сервер. Руководство по выживанию для специалистов по реорганизации бизнеса. Киев: “Диалектика”, 1996, 384 с.).
    К сожалению, несмотря на их огромное количество, рекомендовать книги по Турбо Паскалю очень трудно. Часть из них носит описательный характер, т.е. может использоваться только как справочный материал. Другие претендуют на обучение, но как это делать, трудно понять (мало задач, не разработан “стык” задач с изучаемыми конструкциями и возможностями системы программирования). Поэтому воздержимся от рекомендаций.

Продолжение (вторая часть книги “Основы программирования”)

Предисловие ко второй части

    В первой части книги “Основы программирования” были рассмотрены основные управляющие конструкции языка программирования Турбо Паскаль. Целевой установкой занятий, описанных в первой части (всего было описано 9 занятий), было использование при решении задач минимального числа инструкций. В процессе занятий было необходимо достичь такого уровня их понимания, чтобы работа программы воспринималась школьниками в динамике. Им необходимо “видеть” эту работу, динамику изменения значений переменных в процессе работы программы. С этой целью на первых занятиях использовалась “ручная” трассировка программы, а затем — средства отладчика системы программирования. Таким образом, закладывался первый “кирпичик” в фундамент структурного стиля мышления.
    Вторая часть учебника посвящена второму “кирпичику” нашего фундамента — механизму использования процедур и функций.
    Материал, так же, как и в первой части, разбит на занятия. Однако одно занятие — это не обязательно один урок или пара (и даже чаще всего это не так). Сколько времени потратить на то или иное занятие, должен решать учитель. Приведем пример. Одну из программ четвертого занятия (она приводится ниже) автору иногда приходилось объяснять 5 минут, а иногда — два урока (да и тех не хватало).

Program My4_3;
Begin
    WriteLn (1365 And 2730);
    WriteLn (1365 Or 2730);
    WriteLn (1365 Xor 2730);
    WriteLn (1365 And $FF);
    WriteLn (1365 And $FF0);
    WriteLn (1365 And $FF00);
      ReadLn
End.

    В целом, на наш взгляд, содержание учебника и стиль изложения доступны ученику со средним уровнем подготовки, хотя и для сильного ученика в материале каждого занятия есть достойные задачи и проблемы для исследования.

Занятие 10. Одномерные массивы.
                     Работа с элементами

План занятия
    · раздел описания типов данных;
    · простой пример нахождения суммы чисел;
    · эксперименты с программами поиска суммы элементов массива, кратных заданному числу; нахождения элементов с определенными свойствами в массиве целых чисел; формирования значений элементов массива с помощью генератора случайных чисел; вычисления факториала числа;
    · выполнение самостоятельной работы.

Описание типов данных

    На предыдущих занятиях мы рассматривали только два типа данных: Integer и Boolean. Эти типы относятся к простым. Тип переменной определяет множество значений, которые она может принимать, и операции, которые могут быть над ней выполнены. С каждой переменной может быть связан только один тип данных. Естественно, типами Integer и Boolean не исчерпывается весь список типов Турбо Паскаля. Он не исчерпывается и всеми стандартными типами, ибо в языке есть возможность конструирования новых типов данных. Однако, так или иначе, любой тип данных, описанный программистом, сводится к простым типам (состоит из элементов простых типов). Описание типов данных имеет следующий вид:

Type <имя типа>=<тип данных>;

    После этого в разделе описаний переменных можно описывать переменные данного типа:

Var <имя переменной>:<имя типа>;

    Рассмотрим простой пример. Необходимо найти сумму пяти целых чисел.

Program My10_1;
Var a1,a2,a3,a4,a5,s: Integer;
Begin
    WriteLn ('Введите пять целых чисел');
    ReadLn(a1,a2,a3,a4,a5);
    s:=a1+a2+a3+a4+a5;
    WriteLn ('Их сумма равна ',s)
    ReadLn
End.

    А если требуется найти сумму 30 целых чисел? Аналогичное решение потребует введения 30 однотипных переменных.
    Одномерный массив — это фиксированное количество элементов одного типа, объединенных одним именем. Каждый элемент имеет свой номер. Обращение к элементам массива осуществляется с помощью указания имени массива и номера элементов.
    Для решения нашей задачи потребуется массив из 30 целых чисел.
    Опишем новый тип — одномерный массив, состоящий из 30 целых чисел.

    Type MyArray = Array [1..30] Of Integer;

    Напомним, что раздел описания типов начинается со служебного слова Type, далее перечисляются имена типов и их описания. Между именем типа и его описанием ставится знак “=” (в разделе переменных между именем переменной и ее описанием ставится двоеточие). В нашем случае MyArray — имя нового типа данных; Array — служебное слово (в переводе с английского означает “массив”, “набор”); [1..30] — в квадратных скобках указывается номер первого элемента, затем, после двух точек, номер последнего элемента массива; Of — служебное слово; Integer — тип элементов массива. Решение нашей задачи с использованием массива выглядит следующим образом:

Program My10_1m;
    Const n=30;
    Type MyArray=Array[1..n] Of Integer;
    Var A : MyArray;
             s,i: Integer;
    Begin
        WriteLn ('Введите ',n, ' чисел');
         For i:=11 To n Do ReadLn (A[i]);
         s:=0;
       For i:=1 To n Do s:=s+A[i];
        WriteLn ('Их сумма равна ',s);
          ReadLn
      End.

Экспериментальный раздел занятия

    1. Найдем сумму элементов массива, кратных заданному числу.
    Для этого потребуется внести незначительные изменения в решение предыдущей задачи. Добавляется описание еще одной переменной для хранения значения числа, на кратность которому проверяются значения элементов массива. Появляются операторы

WriteLn ('Введите число ');
ReadLn(k);                           

и изменяется оператор из тела цикла

If A[i] Mod k=0 Then s:=s+A[i];

    Примечание. Не забудьте изменить значение n. Вводить при каждом запуске программы 30 чисел — утомительное занятие.

    Изменим теперь программу так, чтобы в ней определялось количество положительных и отрицательных элементов в данном массиве. Суть основного изменения программы заключается во введении двух переменных (счетчиков — pos, neg) для хранения значений количества положительных и отрицательных элементов в массиве. Где в программе должны быть расположены следующие строки?

pos, neg:Integer;
pos:=0;neg:=0;
If A[i]>0 Then Inc (pos)
              Else If A[i]<0 Then Inc (neg);
WriteLn(pos:4,neg:4);

    Модифицируйте программу таким образом, чтобы в ней находилось и количество нулевых элементов.
    Затем измените программу так, чтобы в массив B записывались номера четных элементов массива A. Введение массива B и работа с ним требуют введения дополнительной переменной для обращения к элементам массива B. Суть решения заключается в просмотре элементов массива A (это мы умеем), выявлении четных элементов и записи их номеров на очередную позицию в массив B.

     Примечание. Обратите внимание на то, что мы записываем не значения элементов, а их номера! Различие между этими понятиями осознается учащимися не сразу, на это надо специально обращать внимание.

Program My10_2;
    Const n=10;
    Type MyArray=Array[1..n] Of Integer;
    Var A,B: MyArray;
           i,j  : Integer;
      Begin
          WriteLn ('Введите ',n, ' чисел');
          For i:=1 To n Do ReadLn (A[i]);
        j:=0;
        For i:=1 To n Do
             If A[i] mod 2 =0 Then Begin
                                                                 Inc(j);
                                                    B[j]:=i
                                                        End;
          For i:=1 To j Do Write (B[i]:3);
        WriteLn;
        ReadLn
    End.

    2. Научимся определять, есть ли в массиве элемент с определенными свойствами, например, отрицательный. Более точно — найдем номер последнего отрицательного элемента.
    Приведем фрагмент очевидного решения:

k:=0;
For i:=1 To n Do
    If A[i]<0 Then k:=i;
If k=0 Then <отрицательных элементов в массиве нет>
Else <последний отрицательный элемент имеет номер i >;

    Это решение плохое. Действительно, если единственный отрицательный элемент в массиве находится на первом месте, то мы выполняем много лишних сравнений, просматривая массив до конца. Договоримся о том, что наш программный код должен экономно, рационально использовать ресурсы компьютера, в частности, и время его работы. Эффективный алгоритм значит в Computer Science больше, чем сверхбыстродействующий компьютер. Следующее изменение 
If A[i]<0 Then Begin k:=i; Break End;
решает возникший вопрос, но… Это изменение приводит к тому, что наш небольшой фрагмент кода имеет одну точку входа и две точки выхода. Тоже плохо, очень плохо. Обилие операторов Break, Goto превратит нашу программу в “спагетти”. И еще одно замечание. При решении элементарной задачи использованы две переменные, хотя этого вовсе не требуется. Приемлемый вариант решения имеет вид:

i:=n;
While (i>=1) And (A[i]>0) Do Dec(i);
If i<1 Then <отрицательных элементов в массиве нет>
Else <последний отрицательный элемент имеет номер i >;

    Чуть изменим задачу. Пусть нам требуется найти значения и номера всех отрицательных элементов. В этом случае можно использовать оператор For, поскольку нам необходимо просмотреть все элементы массива.

{$R+}
Program My10_3;
    Const n=7;
    Type MyArray=Array[1..n] Of Integer;
    Var A:MyArray;
             i:Integer;
    Begin
        WriteLn ('Ввод элементов массива. Не забудьте об отрицательных элементах.');
         For i:=1 To n Do Read (A[i]);
        WriteLn ('Вывод отрицательных элементов массива и их номеров (индексов)');
          For i:=1 To n do
            If A[i]<0 Then WriteLn (A[i]:5,i:5);
           Readln
      End.

    В тексте программы поиска номеров всех отрицательных элементов в массиве имеются строки:

For i:=1 To n

    Измените во второй строке n на n+1 и поставьте перед текстом программы директиву компилятора {$R+}. При запуске программы появится ошибка периода выполнения: Error 201: Range check error. Она является сообщением о том, что значение переменной i (индекс элемента массива A) вышло за допустимый предел, т.е. за значение константы n.

    Директивы компилятора управляют режимами компиляции. Все директивы начинаются с символа $ после открывающей скобки комментария, за которым следует имя директивы (состоящее из одной или нескольких букв), определяющее ее назначение. Контроль диапазонов включается / выключается посредством директив {$R+}/{$R-}. В режиме {$R+} все индексы массивов и строк контролируются на выход за границы, а все присваивания значений скалярных переменных и ограниченных типов проверяются на вхождение в диапазон. При выходе за границы выполнение программы прекращается и выдается сообщение об ошибке.

     Примечание. При работе с массивами настоятельно рекомендуется использовать эту директиву при отладке программ.

    3. Формирование значений элементов массива путем ввода их с клавиатуры — достаточно утомительное занятие. Давайте попробуем использовать для этих целей генератор случайных чисел. Это сложное название мы будем понимать очень просто. Есть нечто (“черный ящик”), и это нечто выдает числа, причем нам неизвестно, какое число выдается в очередной раз. Этим “черным ящиком” в Турбо Паскале является функция Random. Она возвращает случайное число.

    Примечание. С типом Real мы еще не работали.

{$R-}
Program My10_4;
    Const n=10;
    Type MyArray=Array[1..n] Of Integer;
    Var A:MyArray;
            i:Integer;
    Begin
        {Randomize;}
        WriteLn ('Формирование значений элементов массива A');
          For i:=1 To n Do A[i]:=Random (21) {-10};
        WriteLn ('Вывод');
        For i:=1 To n Do Write (A[i]:5);
        ReadLn
     End.

    Запустите эту программу несколько раз. На экран будет выведена одна и та же последовательность чисел в диапазоне от 0 до 20. Уберите фигурные скобки у —10 и снова запустите несколько раз программу. Последовательность чисел на экране снова одна и та же, но числа теперь находятся в интервале от —10 до 10. Объясните этот факт. Попробуйте получать числа из любого интервала, например, от —17 до 25. Продолжим наши эксперименты. Уберите фигурные скобки у процедуры Randomize. Повторите многократный запуск программы. Теперь последовательности чисел на экране разные. В чем дело? Наш “черный ящик”, функция Random, начинает генерировать в первом случае числа (каким-то не известным нам образом) от фиксированного начального числа. Во втором случае эти начальные числа меняются от запуска к запуску (процедурой Randomize), и последовательности получаются разные. Следующим изменением является включение контроля на выход за допустимый диапазон {$R+}. После запуска мы видим уже знакомую ошибку: Error 201: Range check error. Прочитайте еще раз внимательно описание функции Random и попробуйте найти объяснение причины возникновения ошибки.

    Рассмотрим еще одну программу:

{$R+}
Program My10_4m;
    Const n=10;
    Var i:Integer;
     Begin
          WriteLn ('Вывод 10 случайных чисел в диапазоне от –10 до 10');
         For i:=1 To n Do WriteLn (Random (21)-10);
          ReadLn
      End.

    После запуска этой программы на экране появятся не числа из интервала от —10 до 10, а какая-то странная последовательность чисел. Она может быть, например, такой: 65530, 1, 2, 4, 65527, 2, 65528, 65534, 3, 2. Почему? Напомним, что диапазон для целых чисел типа Word от 0 до 65535 и число 65535₁₀ = 2¹⁶ —1 = 1111111111111111₂ , а это —1 в дополнительном коде. Число 65534 соответствует —2 в дополнительном коде. В первой версии программы результат функции Random имеет тип Word. Из этого числа вычитается целое число типа Integer. Поскольку типы различные, выполняется преобразование типов по правилу, описанному в занятии 2, то есть к типу LongInt. А элемент массива имеет тип Integer. Вот здесь-то и “собака зарыта”. Измените тип элементов массива A на LongInt и сравните результаты работы программ.

    4. Научимся вычислять факториал натурального числа N. Факториал числа N равен произведению чисел 1•2•3•…•(N—1)•N (обозначается как N!). Сложность задачи в том, что уже 8! = 40320, а 13! = 6227020800. Таким образом, типы данных Integer, LongInt можно использовать лишь для вычисления факториалов совсем небольших чисел. Для представления факториала договоримся использовать массив. Приведем пример:

    В массиве записано значение 11! = 39916800. В A[0] фиксируется число занятых элементов массива, в A[1] находится цифра единиц результата, в A[2] — цифра десятков результата, в A[3] — цифра сотен результата и т.д. Почему так, а не наоборот? Такая запись позволяет исключить сдвиг элементов массива при переносе значений в старший разряд. А сейчас наберите, как обычно, текст программы, выполните компиляцию и, открыв окно Watch, выполните приведенную ниже программу в пошаговом режиме, отслеживая изменение значений переменных при не очень большом значении N. Добейтесь полного понимания логики работы программы.

{$R+}
Program My10_5;
    Uses Crt;
    Const MaxN=300;
    Type MyArray=Array[0..MaxN] Of Integer;
    Var A:MyArray;
    Var i,j,r,w,N:Integer;
    Begin
          ClrScr;
        FillChar (A,SizeOf (A),0); {Заполняем массив А нулями.}
         WriteLn ('Введите число, факториал которого необходимо найти.');
           ReadLn(N);
           A[0]:=1;A[1]:=1;j:=2;{Начальные присваивания, начинаем вычислять 2!.}
           While (j<=N) аnd (A[0]<MaxN) Do Begin {Второе условие фиксирует факт выхода за пределы массива.}
                r:=0;i:=1;{r – перенос из разряда в разряд при выполнении умножения числа j на очередную цифру A[i] предыдущего результата.}
                While (i<=A[0]) or (r<>0) Do Begin{Пока не "прошли" все цифры предыдущего результата или есть перенос цифры в старший разряд.}
                  w:=A[i]*j+r;{Умножаем очередную цифру и прибавляем цифру переноса из предыдущего разряда.}
                  A[i]:=w mod 10;{Находим новую цифру с номером i.}
                  r:=w div 10;{Вычисляем значение переноса.}
                  If A[A[0]+1]<>0 Then Inc(A[0]);{Изменяем, если необходимо, количество задействованных элементов массива A, длину полученного результата.}
                  Inc(i)
                 End;
                 Inc(j)
         End;
           For i:=A[0] DownTo 1 Do Write(A[i]);{Вывод результата.}
             WriteLn;
            ReadLn
    End.

    Найдите число N, при котором трехсот элементов массива A окажется недостаточно для хранения результата.
    Измените программу так, чтобы выводились факториалы всех чисел в интервале от 1 до N.
    Измените программу так, чтобы в ней вычислялись числа вида aⁿ , например, 3¹⁰⁰ .

Задания для самостоятельной работы

    1. Дан массив целых чисел. Найти:
    · сумму элементов массива, больших данного числа А, А вводится с клавиатуры;
    · сумму элементов массива, принадлежащих промежутку от А до В (А и В вводятся с клавиатуры);
    · максимальный элемент массива и его номер, при условии, что все элементы различны;
    · номера всех элементов массива с максимальным значением;
    · минимальный элемент массива;
    · сумму элементов массива с k₁-го по  k₂-й,  k₁ и  k₂   вводятся с клавиатуры;
    · количество нечетных элементов массива;
    · количество отрицательных элементов массива;
    · сумму первых пяти элементов массива;
    · все элементы, кратные 3 или 5, и их количество;
    · сумму всех четных элементов массива, стоящих на четных местах, то есть имеющих четные номера;
    · сумму всех четных элементов массива (или сумму элементов, кратных заданному числу);
    · сумму положительных элементов массива;
    · сумму элементов, имеющих нечетное значение;
    · сумму элементов, имеющих нечетные индексы;
    · сумму положительных элементов, значения которых меньше 10;
    · удвоенную сумму положительных элементов;
    · сумму отрицательных элементов;
    · индексы тех элементов, значения которых больше заданного числа А;
    · количество элементов массива, значения которых больше заданного числа А и кратны 5;
    · индексы тех элементов, значения которых кратны 3 и 5;
    · индексы тех элементов, значения которых больше значения предыдущего элемента (начиная со второго);
    · количество тех элементов, значения которых положительны и не превосходят заданного числа А;
    · пару соседних элементов с суммой, равной заданному числу.
    2. Определить:
    · сколько элементов массива превосходят по модулю заданное число А;
    · есть ли в данном массиве два соседних положительных элемента? Найти номера первой (последней) такой пары;
    · есть ли в данном массиве элементы, равные заданному числу? Если есть, то вывести номер одного из них;
    · есть ли в данном массиве положительные элементы, кратные k, k вводится с клавиатуры;
    · номер первого отрицательного элемента, дающего при делении на 5 остаток 2;
    · есть ли 2 пары соседних элементов с одинаковыми знаками;
    · номер последней пары соседних элементов с разными знаками.
    3. Измените программу вычисления факториала числа N так, чтобы вычислялись: 1•3•5•…•(2•N—1), 2•4•6•8•…•(2•N).
    4. Измените программу вычисления степени числа так, чтобы была возможность вычислять степени отрицательных целых чисел.
    5. Измените программу вычисления степени числа так, чтобы в степень возводились рациональные числа.

Материал для чтения

1. Одномерный массив — это конечное упорядоченное множество элементов. За первым элементом идет второй, за вторым — третий и т.д. В силу этого элементы массива можно перенумеровать целыми числами — индексами элементов. Для доступа к элемен ту массива достаточно знать имя массива и индекс элемента. Память компьютера представляет собой последовательность ячеек, имеющих адреса, с возможностью обращения к ячейкам по их номерам. Для массива обычно выделяется сплошной участок памяти компьютера. Как вычисляются адреса элемента массива в памяти? С этой целью массив имеет описатель (дескриптор). Приведем структуру дескриптора, например, для массива A: Array[1..10] Of Integer.

Адрес элемента A[i] находится по формуле: 
Addr(A[i])=Addr(A[1])+(i-1)*2

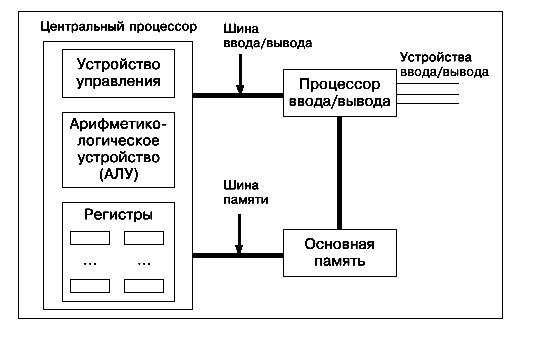
    2. Общие сведения по организации ЭВМ. Структура простой ЭВМ показана на рисунке.
    “Мозгом” вычислительной машины является центральный процессор. Его функция состоит в выполнении программ, находящихся в основной памяти, путем выборки, проверки и последовательного выполнения составляющих их команд. Центральный процессор состоит из нескольких частей. Устройство управления осуществляет выборку команд из основной памяти и определение их типа. Арифметическо-логическое устройство осуществляет выполнение таких операций, как сложение, сдвиг и т.д. Центральный процессор содержит высокоскоростную память для запоминания промежуточных результатов и управляющей информации. Эта память состоит из регистров, каждый из которых имеет определенное назначение. Счетчик команд указывает адрес команды, которую необходимо выполнить следующей. Регистр команд содержит текущую выполняемую команду. Центральный процессор выполняет каждую команду в виде последовательности простых операций:
    · выбор очередной команды из основной (оперативной) памяти в регистр команд;
    · изменение счетчика команд таким образом, чтобы он указывал на адрес команды, следующей за выбранной;
    · определение типа выбранной команды;
    · проверка, требуются ли для выполнения выбранной команды какие-либо данные, и если они нужны, то определение их адресов в памяти;
    · загрузка во внутренние регистры центрального процессора требуемых данных из памяти;
    · выполнение команды;
    · запоминание результатов выполнения команды в заданных ячейках памяти.
    Память — это часть ЭВМ, где хранятся программы и данные. Память состоит из ячеек (ячейка — минимальная адресуемая единица памяти), каждая из которых может хранить данные. Каждой ячейке соответствует число, называемое ее адресом. Если в памяти N ячеек, то они имеют адреса от 0 до N—1. Все ячейки памяти содержат одинаковое число битов. Если в ячейке k битов, то она может содержать любую из 2^k их комбинаций. Центральный процессор связан с основной памятью при помощи как минимум двух регистров — регистра адреса памяти и буферного регистра. Для того чтобы считать из памяти содержимое ячейки, центральный процессор загружает адрес этой ячейки в регистр адреса памяти и посылает памяти сигнал чтения. Память помещает содержимое запрашиваемой ячейки в буферный регистр, где оно доступно центральному процессору для последующей обработки. Для того чтобы записать данное в память, центральный процессор записывает адрес ячейки памяти в регистр адреса памяти и записываемое данное в буферный регистр, а затем сигнализирует памяти о начале операции записи.
    3. Принципы Джона фон Неймана. Несмотря на большие разнообразия существующих в настоящее время
ЭВМ, в основы их заложены некоторые общие принципы. Эти принципы были сформулированы в 40-х годах ХХ столетия выдающимся американским математиком Джоном фон Нейманом и позволили создать устройство обработки информации с достаточно простыми и универсальными принципами работы. Это устройство и называется ЭВМ. Первый принцип — принцип произвольного доступа к основной (оперативной) памяти. Структурно основная память, как мы говори ли, состоит из ячеек. Принцип гласит о том, что процессору в каждый момент времени доступна любая ячейка, причем время доступа (чтения или записи) одинаково для всех ячеек. Чтобы обеспечить такой доступ, ячейки памяти должны иметь свои уникальные имена. Этими именами являются номера ячеек. Для лучшего понимания действия этого принципа можно сравнить этот доступ с доступом к данным на магнитной ленте (например, магнитофонной). Данные, записанные на магнитной ленте, также можно разбить на элементарные единицы — слова. При произвольном положении магнитной ленты доступно лишь то слово, которое находится под головками чтения — записи. Для чтения слова на другом участке магнитной ленты необходимо предварительно переместить этот участок под блок головок, то есть доступ к этому слову возможен лишь после просмотра предыдущих участков магнитной ленты. Поэтому магнитную ленту принято называть памятью с последовательным доступом. 
    Второй фундаментальный принцип Джона фон Ней мана — принцип хранимой программы. Программа решения задачи хранится в оперативной памяти наряду с обрабатываемыми данными. В принципе ЭВМ не различает, что именно хранится в данной ячейке памяти — число, символ или команда. Для решения другой задачи требуется смена в оперативной памяти программы и обрабатываемых данных. Итак, ЭВМ — универсальный инструмент обработки информации.
    4. Возникновение информатики как науки связано с появлением ЭВМ и относится к 60-м годам ХХ столетия. В самом общем смысле под информатикой пони мают фундаментальную науку, изучающую процессы передачи, накопления и обработки информации с помощью ЭВМ.
    Термин “Informatique” введен во Франции на рубеже 60—70-х годов. Однако еще раньше в США был введен в употребление термин “Computer Science” для обозначения науки о преобразовании информации с помощью ЭВМ. В настоящее время эти термины практически эквивалентны. Содержание ядра информатики, на наш взгляд, определяют программные и технические средства.
    На этом занятии рассмотрено понятие массива, а в материале для чтения дан обзор структуры простой ЭВМ и принципов Джона фон Неймана. Понятие массива носит фундаментальный характер. Эта структура данных наиболее соответствует структуре ЭВМ. Образно выражаясь, оперативная память ЭВМ — это не что иное, как огромный одномерный массив.

Продолжение следует