Вы - -й посетитель этой странички
Представление информации, системы счисления и основы логики
В.С. Голубев, г. Тверь
Предлагаемые вашему вниманию конспекты
уроков по теме “Представление информации,
системы счисления и основы логики” созданы
на основе требований, предъявляемых “Примерной
программой курса информатики” 10—11-х
классов (136 часов, т.е. 2 часа в неделю).
Программа предусматривает выделение на эту
тему 28 учебных часов, однако думается, что
такое количество уроков на эту тему
отводить нецелесообразно. Получившуюся экономию учебного времени,
по моему мнению, необходимо затратить на более
глубокое изучение темы “Алгоритмизация и
программирование”.
Приложением к конспектам являются три
программы, позволяющие учителю с минимальной
потерей времени провести проверку знаний учащихся по
вопроам, рассматриваемым на уроках.
• Программа “Перевод” позволяет ввести
двоичное число из не более 16 двоичных знаков и
получить его десятичный эквивалент.
• Программа “Логэл” позволяет провести
тестирование знаний учащимися принципов работы
логических элементов компьютера.
• Программа “Сумматор” позволяет
провести тестирование знаний учащимися принципов
работы сумматора.
Автор будет благодарен всем за замечания
и предложения по предлагаемым конспектам.
Урок 1
Темы. Информация. Способы и формы
представления информации. Кодирование. Двоичное
кодирование. Единицы измерения информации.
Цель. Изучить понятие информации, ее
свойств, единицы измерения информации.
Ход урока
I. Изложение нового материала (рассказ учителя)
Термин “информация” происходит от
латинского слова informatio — разъяснение, изложение,
осведомленность. Информацию друг другу мы
передаем в устной и письменной форме, в форме жестов,
мимики, знаков. Информацию мы получаем, передаем
другим и делаем определенные умозаключения на ее
основе.
В любом виде информация выражает сведения
о ком-то или о чем-то, и при этом она обязательно
имеет некоторую форму — форму рассказа, рисунка,
статьи и т.д. Чертежи и музыкальные произведения, книги
и картины, спектакли и фильмы — все это формы
представления информации.
Поэтому информация в наиболее общем
понимании — это отражение предметного мира с
помощью знаков и сигналов. Получение информации —
это в конечном счете получение фактов, сведений
и данных о свойствах, структуре или взаимодействии
объектов и явлений окружающего нас мира.
Предметное содержание информации
позволяет уяснить ее основные свойства: актуальность,
доступность, полноту, достоверность.
В процессе развития человеческого
общества люди выработали большое число языков. Среди
них — язык жестов и мимики, язык рисунков и чертежей,
язык музыки, разговорные языки и т.д.
Примеры:
1. Язык жестов — морской флажковый семафор.
2. Язык музыки — ноты.
3. Языки программирования.
Основой большинства языков является алфавит. Алфавит — это набор символов, из которых можно составить слова и фразы данного языка.
Примеры:
1. Латинский алфавит (прописные буквы):
A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z.
2. Русский алфавит (прописные буквы): А, Б, В,
Г, Д, Е, Ё, Ж, З, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч,
Ш, Щ, Ъ, Ы, Ь, Э, Ю, Я.
3. Алфавит десятичных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8,
9.
4. Алфавит двоичных цифр: 0, 1.
Простота двоичного алфавита обеспечила
его широкое применение в вычислительной технике.
Значения 0 и 1 в компьютерах представляются
физическими состояниями “намагничено — не намагничено”,
“есть напряжение — нет напряжения”. В
вычислительной технике для двоичных цифр 0 и 1 принят
специальный термин — бит. Бит — от английского
сокращения bit (binary digit — двоичная цифра).
Представление символов некоторого
алфавита словами из нулей и единиц называется двоичным
кодированием. Двоичный код должен быть такой длины,
чтобы он обеспечивал кодирование всех символов
алфавита.
Из двух битов можно составить четыре
различные комбинации: 00, 01, 10, 11, из трех — восемь, из
четырех — шестнадцать различных комбинаций —
и т.д.
Запись на доске:
2 бита — 4 комбинации = 22,
3 бита — 8 комбинаций = 23,
4 бита — 16 комбинаций = 24,
5 бит — 32 комбинации = 25,
6 бит — 64 комбинации = 26,
7 бит — 128 комбинаций = 27,
8 бит — 256 комбинаций = 28.
Набор из восьми бит называется байтом.
1 байт = 8 бит.
Более крупные единицы измерения
информации:
1 килобайт = 1024 байтам = 210 байтам.
1 мегабайт = 1024 килобайтам = 210 килобайтам =
220 байтам.
1 гигабайт = 1024 мегабайтам = 210 мегабайтам =
220 килобайтам = 230 байтам.
II. Закрепление изученного материала
1. Какие еще языки вы знаете?
2. Является ли языком азбука Морзе?
3. Из каких символов состоит язык азбуки
Морзе?
4. Что такое бит?
5. Что такое байт?
6. Компьютер имеет оперативную память 32 Мб.
Сколько бит это составляет?
III. Домашнее задание
Конспект.
Урок 2
Тема. Системы счисления.
Цель. Формирование первоначальных
представлений о системах счисления.
Ход урока
I. Изложение нового материала (лекция)
1. Понятие системы счисления.
Система счисления — способ записи чисел с
помощью заданного набора специальных знаков (цифр).
С первого класса вы изучали десятичную
систему счисления, в которой для записи чисел
использовались десять хорошо известных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
2. Позиционная и непозиционная системы
счисления.
Пример непозиционной системы счисления —
римская система, позиционной — арабская (современная
десятичная).
3. Особенности строения позиционной
системы счисления на примере десятичной.
Значение каждой цифры (ее “вес”) зависит
от ее места (позиции) при написании числа.
Положение (позиция) цифры в записи числа определяет
ее разряд; если в числе отсутствует какой-либо
разряд, то в записи числа на его место ставят цифру 0. Мы знаем,
что 10 единиц любого разряда образуют новую
единицу старшего разряда. Число 10 называется
основанием десятичной системы счисления. С его помощью
определяется “вес” единицы каждого разряда.
4. Формирование понятия систем счисления с
разными основаниями.
Вопрос: Сколько цифр используется в 12-ричной
системе счисления?
Ответ: Двенадцать.
Вопрос: Во сколько раз “вес” единицы
одного разряда будет больше или меньше “веса”
единицы соседнего разряда в 12-ричной системе счисления?
Ответ: В 12 раз.
Вопрос: Сколько цифр используется в 8-ричной
системе счисления?
Ответ: Восемь.
Вопрос: Во сколько раз “вес” единицы
одного разряда будет больше или меньше “веса”
единицы соседнего разряда в 8-ричной системе счисления?
Ответ: В 8 раз.
5. Перевод целых чисел из системы
счисления с основанием p в десятичную систему счисления.
Перевод выполняется по правилу:
anan-1 … a2a1p =
an • pn-1 + an-1
• pn-2 + … + a2 • p1 +
a1 • p0 .
Привести примеры.
6. Перевод целых чисел из десятичной
системы счисления в систему счисления с другим
основанием.
Перевод выполняется методом деления
целого десятичного числа на основание новой системы
счисления.
Пример: Перевести десятичное число 443 в
пятеричную систему счисления.
Ответ: 44310 = 32335.
7. Решение задач.
Задача 1. Перевести в восьмеричную систему
счисления десятичные числа: 198; 437; 2418.
Ответы: 3068 ; 6658 ; 45628.
Задача 2. Существует ли система счисления,
в которой 8 + 1 = 10 и 3 • 4 = 13?
Решение: Предположим, что существует
такая система счисления с основанием р.
Тогда:
| 8 • p0 + 1 • p0 = 1 • p | |
| 3 • p0 + 4 • p0 = 1 • p1 + 3 • p0 , следовательно, |
| |
9 = p |
| 12 = p + 3, |
Ответ: Такое соотношение выполняется в 9-ричной
системе счисления.
8. При наличии времени можно решить
следующие задачи:
Задача 1. Запишите наибольшее двузначное
число в восьмеричной, пятеричной, троичной
системах счисления. Определите десятичные эквиваленты
этих чисел.
Задача 2. Запишите наименьшее трехзначное
число в восьмеричной системе счисления, в
пятеричной системе счисления, в троичной системе счисления и
определите его десятичный эквивалент для записанных
чисел.
Задача 3. В классе 101002 девочек и 11002 мальчиков. Сколько учеников в классе?
Ответ: В классе 32 ученика.
III. Домашнее задание
Изучить конспект. Решить оставшиеся задачи.
Урок 3
Тема. Двоичная система счисления.
Цель. Рассмотреть правила двоичной
арифметики.
Ход урока
I. Повторение
1. Фронтальный опрос:
а) что мы понимаем под системой счисления;
б) в чем принципиальная разница между
позиционной и непозиционной системами счисления;
в) что называется основанием системы
счисления?
II. Изучение нового материала
1. Вопрос: Во сколько раз “вес” единицы
одного разряда двоичной системы счисления
отличается от “веса” соседнего разряда?
Ответ: В 2 раза.
Вопрос: Сколько цифр
используется в двоичной системе счисления? |
|
3. Перевод чисел из двоичной системы
счисления в десятичную систему счисления был
рассмотрен на прошлом уроке.
4. Представление целых чисел в памяти ЭВМ.
Каждое целое число занимает два байта (две
ячейки) в памяти компьютера, т.е. 16 разрядов.
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
Старший разряд отводится под знак числа. У
положительных чисел в старшем разряде
находится 0, а у отрицательных — 1. Таким образом можно
закодировать числа в диапазоне от —32 768 до 32 767.
Отрицательные числа кодируются в
дополнительном коде.
Правила создания дополнительного кода:
1) Все биты модуля двоичного числа
инвертируются.
2) К полученному числу прибавляется 1.
Примеры:
2
0000000000000010
3
0000000000000011
9
0000000000001001
10
0000000000001010
15
0000000000001111
32 766
0111111111111110
32 767
0111111111111111
—3
11111111 11111101
—9
11111111 11110111
—32 767
10000000 00000001
—32 768
10000000 00000000
5. Представление вещественных чисел в
памяти ЭВМ.
Вещественные числа в памяти компьютера
представляются в нормализованной форме. Она
позволяет существенно расширить диапазон
представляемых величин. Нормализованной формой
представления чисел называется число, записанное в виде:
А = ± mpn ,
— где m — мантисса, р — основание системы
счисления, n — порядок.
Мантисса m должна удовлетворять условию:
1/p £
m < 1.
Из условия видно, что мантисса — это
правильная дробь, в которой первая после запятой
цифра отлична от нуля.
Вещественное число занимает в памяти
компьютера, как правило, минимум четыре байта. Из
них три младших байта занимает мантисса, а
старший байт имеет вид:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | ||||||||
|
|
|||||||||||||||
| Знак m | Знак n | n | |||||||||||||
6. Решение задач.
Представить в дополнительном коде
десятичные числа:
| Число | Ответ |
| -37 | 1111111111011011 |
| -86 | 1111111110101010 |
| -165 | 1111111101011011 |
| -516 | 1111110111111100 |
| -2433 | 1111011001111111 |
III. Домашнее задание
Конспект, решить оставшиеся примеры.
Урок 4
Тема. Двоичная арифметика.
Цель. Рассмотреть правила двоичной
арифметики.
Обеспечение урока. Программа “Перевод”.
Ход урока
I. Повторение ранее изученного материала
1. Фронтальный опрос:
а) что мы понимаем под системой счисления;
б) в чем принципиальная разница между
позиционной и непозиционной системами счисления;
в) какие характеристики системы счисления
определяет ее основание;
г) почему двоичная система счисления
наиболее удобна для представления и обработки
информации в компьютере;
д) какие вы видите недостатки двоичной
системы счисления?
2. Самостоятельная работа. Каждому
учащемуся продиктовать четырехзначное натуральное
число и проверить правильность перевода в двоичную
систему при помощи программы “Перевод”.
II. Изучение нового материала
1. Сложение чисел в двоичной системе
счисления.
Запись на доске:
2
10 0000000000000010
+3
+11 + 0000000000000011
5
101 0000000000000101
При сложении чисел надо обязательно
проговаривать алгоритм сложения. Следует учитывать,
что сложение, как обычно, нужно начинать с
младшего разряда. Если сумма единиц разряда окажется
равной или большей основания системы счисления, то
возникает перенос единицы в старший разряд. После
сложения cледует обязательно сделать обратный
перевод и убедиться, что число 101 — действительно число
5 в десятичной системе счисления.
2. Вычитание двоичных чисел. В компьютере
вычитание заменяется сложением с
отрицательным числом, представленным в дополнительном коде.
Запись на доске:
14
1110 0000000000001110
-9
+1001 +1111111111110111
5
101 10000000000000101
Так как под целое число отводится 16
разрядов, то старшая единица теряется. Ответ
получается 101.
3. Умножение чисел в двоичной системе
счисления.
110
*101
110
+ 000
110
11110
Подчеркиваем, что при умножении 1•1 = 1 и
1•0 = 0. Анализируя примеры умножения в
двоичной системе счисления, необходимо
обратить внимание учащихся на важную особенность
выполнения этой операции в данной системе счисления. Так
как очередная цифра множителя может быть только 1
или 0, то промежуточное произведение равно либо
множимому, либо 0. Таким образом, операция
умножения в двоичной системе фактически не
производится: в качестве промежуточного произведения
записывается либо множимое, либо 0, а затем
промежуточные произведения суммируются. Иначе говоря,
операция умножения заменяется последовательным
сложением.
4. Решение примеров.
1) Записать десятичные числа в двоичной
системе счисления в дополнительном коде: —8; —65;
—48.
2) Выполнить действия в двоичной системе
счисления: 65•5; 27 — 13.
III. Домашнее задание
Конспект. Решить оставшиеся задачи.
Урок 5
Тема. Восьмеричная и шестнадцатеричная
системы счисления.
Цель. Ознакомить учащихся с восьмеричной
и шестнадцатеричной системами счисления.
Показать преимущества представления чисел в данных
системах по сравнению с двоичной.
Ход урока
I. Повторение ранее изученного материала
Решение примеров:
1. Записать десятичные числа в двоичной
системе счисления в дополнительном коде: —13; —27;
—36.
2. Выполнить действия в двоичной системе
счисления: 9•13; 256 — 36.
II. Содержание нового материала
1. Восьмеричная и шестнадцатеричная
системы счисления.
В восьмеричной системе счисления числа
записываются с помощью восьми цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Сама восьмерка (как и основание любой системы
счисления) записывается двумя цифрами: 10 (почему?).
Для записи чисел в шестнадцатеричной системе
счисления необходимо располагать уже шестнадцатью
различными символами, используемыми как цифры. В
качестве первых десяти шестнадцатеричных цифр
используются цифры десятичной системы счисления. Для
обозначения остальных шести цифр (в десятичной
системе они соответствуют числам 10, 11, 12, 13, 14, 15)
используют буквы латинского алфавита — A, B, C, D, E, F.
Особая привязанность программистов к
восьмеричной и шестнадцатеричной системам счисления
объясняется тем, что переход к записи числа в любой из
этих систем от его двоичной записи очень прост,
так как 8 и 16 являются степенями числа 2.
Полезно привести таблицу:
| Основные системы счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
2. Перевод чисел из двоичной системы
счисления в восьмеричную и шестнадцатеричную системы
счисления.
При переводе в восьмеричную систему
счисления двоичное число из трех и менее цифр
записывается одной восьмеричной цифрой.
При переводе в шестнадцатеричную систему
счисления двоичное число из четырех и менее цифр
записывается одной шестнадцатеричной цифрой.
Пример:
1. Представить двоичное число 1010110101111 в
восьмеричной системе счисления.
1 010 110 101 111
1 2 6
5 7
2. Представить двоичное число 1010110101111 в
шестнадцатеричной системе счисления.
1 0101 1010 1111
1 5
A F
3. Решение примеров.
1) Перевести числа из двоичной системы
счисления в восьмеричную и шестнадцатеричную: 11100011;
101110,1; 111111,01001.
2) Перевести числа из восьмеричной системы
счисления в двоичную: 567; 204,72.
3) Перевести числа из шестнадцатеричной
системы счисления в двоичную: 4D2A; 31,05; 40A,7.
III. Решение задач на закрепление темы “Системы счисления”
Задача 1. Перевести число 76,5 из
восьмеричной системы счисления в шестнадцатеричную.
Задача 2. Перевести число 7142 из десятичной
системы счисления в шестнадцатеричную.
Задача 3. Перевести число 0,225 из десятичной
системы счисления в шестнадцатеричную.
Задача 4. Перевести число 440 из десятичной
системы счисления в двоичную.
Задача 5. Перевести число 110,175 из
десятичной системы счисления в восьмеричную.
Задача 6. Перевести число 9F3A из
шестнадцатеричной системы счисления в десятичную.
Задача 7. В лаборатории 35 386-х компьютеров и
22 486-х компьютера, всего — 101 компьютер. В какой системе счисления записаны числа?
IV. Домашнее задание
Конспект записей.
Урок 6
Тема. Понятие математической логики.
Логические операции.
Цель. Познакомить учащихся с понятием
высказывания и логическими операциями.
Ход урока
I. Самостоятельная работа (25 минут)
1. Перевести двоичное число в десятичную
систему счисления
Вариант 1
Вариант 2
101001011,1011 100001111,0101
Ответ:
331,6875
271,3125
2. Перевести десятичное число в двоичную систему счисления
Вариант 1
Вариант 2
4096
1025
Ответ:
1000000000000 10000000001
3. Перевести восьмеричное число в десятичную систему счисления
Вариант 1
Вариант 2
707
617
Ответ:
455
399
II. Изучение нового материала
Рассказ учителя
История логики насчитывает около двух с
половиной тысячелетий. Она берет начало от
формальной логики Аристотеля. Дальнейшее развитие логики
связано с именами Готфрида Вильгельма Лейбница и
Джорджа Буля, которые разработали математический
аппарат алгебры логики. Именно поэтому алгебру
высказываний и называют булевой алгеброй. Математическая
логика в XIX—XX вв. рассматривалась как базис для
логического обоснования в различных областях математики,
но в последние десятилетия математическая логика
находит применение во многих областях, в частности, в
кибернетике, теории ЭВМ, теории алгоритмов.
Основным понятием математической логики
является понятие высказывания.
Высказывание — предложение, про которое всегда можно
сказать, истинно оно или ложно. Высказывания
бывают простые и сложные. Сложное высказывание
состоит из простых, соединенных знаками логических
операций. Простые высказывания обычно
обозначают большими латинскими буквами: А, В, С, — и т.д.
Рассмотрим следующие логические операции:
не (отрицание), или (конъюнкция),
и (дизъюнкция), ® (следование).
Логические операции определяются через
таблицы истинности.
Пусть имеются два высказывания: А — юноша в школе; В — юноша на уроке. Составим
таблицы, которые показывают смысл
операций и, или, не.
| Операция “и” | ||
| A | B | A и B |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
| Операция “или” | ||
| A | B | A и B |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
| Операция “не” | |
| A | не A |
| И | Л |
| Л | И |
Пусть имеются два высказывания: А — у человека высокая температура, В — человек болен. Составим таблицу, которая показывает смысл операции следования.
| A | B | Из A следует B |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
III. Решение задач
Предложить учащимся самостоятельно заполнить таблицу:
| Формула | Высказывание | Тигр | Волк | Бурундук | Заяц |
| A | Зверь полосатый | ||||
| B | Зверь хищый | ||||
| не A | |||||
| не B | |||||
| A и B | |||||
| A или B |
Ответ:
| Формула | Высказывание | Тигр | Волк | Бурундук | Заяц |
| A | Зверь полосатый | И | Л | И | Л |
| B | Зверь хищый | И | И | Л | Л |
| не A | Зверь не полосатый | Л | И | Л | И |
| не B | Зверь не хищный | Л | Л | И | И |
| A и B | Зверь полосатый и хишный | И | Л | Л | Л |
| A или B | Зверь полосатый или хишный | И | И | И | Л |
IV. Домашнее задание
Изучить конспект.
Урок 7
Тема. Законы математической логики.
Цель. Ознакомить учащихся с законами
математической логики и их доказательством.
Выработать навыки доказательства логических выражений
методом составления таблиц истинности.
Ход урока
I. Фронтальный опрос
1. Дать определение высказывания.
2. Какое высказывание называется сложным?
3. Какие логические операции вам известны?
4. Написать на доске таблицы истинности
логических операций.
II. Изучение нового материала
Выписать на доске и доказать
основные
законы математической логики.
Конъюнкция Дизъюнкция
Отрицание
А и А = А
А или А = А не (не А) = А
А и Л = Л
А или И = И
А и И = А
А или Л = А
Переместительный (коммутативный) закон:
А или В = В или А
А и В = В и А
Сочетательный (ассоциативный) закон:
(А или В) или С = А или (В или С)
(А и В) и С = А и (В и С)
Распределительный (дистрибутивный) закон:
(А и В) или С = (А или С) и (В или С)
(А или В) и С = (А и С) или (А и В)
Закон исключенного третьего:
А или не А = И
Закон противоречия:
А и не А = Л
Формулы де Моргана:
не (А или В) = (не А) и (не В)
не (А и В) = (не А) или (не В)
Формулы склеивания:
(А и В) или (А и не В) = А
(А или В) и (А или не В) = А
Формулы поглощения:
А или (А и В) = А
А и (А или В) = А
III. Практическая работа
1. Проверить истинность формул де Моргана.
Ответ:
| A | B | не A | не B | не (A или B) | (не A) и (не B) |
| И | И | Л | Л | Л | Л |
| И | Л | Л | И | Л | Л |
| Л | И | И | Л | Л | Л |
| Л | Л | И | И | И | И |
| A | B | не A | не B | не (A и B) | (не A) или (не B) |
| И | И | Л | Л | Л | Л |
| И | Л | Л | И | И | И |
| Л | И | И | Л | И | И |
| Л | Л | И | И | И | И |
2. Доказать, что (Х или не Х) и
Y = Y
Ответ:
| X | X | не X | X или не X | (X или не X) и Y |
| И | И | Л | И | И |
| И | Л | Л | И | Л |
| Л | И | И | И | И |
| Л | Л | И | И | Л |
3. Составить таблицу истинности выражения
(не А) или ((не В) и С)
Ответ:
| A | B | C | не B | не A | (не B) и С | (не А) или ( (не В) и С |
| И | И | И | Л | Л | Л | Л |
| И | И | Л | Л | Л | Л | Л |
| И | Л | И | И | Л | И | И |
| Л | И | И | Л | И | Л | И |
| И | Л | Л | И | Л | Л | Л |
| Л | И | Л | Л | И | Л | И |
| Л | Л | И | И | И | И | И |
| Л | Л | Л | И | И | Л | И |
4. Доказать, что А ® В = (не А) или В
| A | B | не A | ( не A) или X | Из A следует В |
| И | И | Л | И | И |
| И | Л | Л | Л | Л |
| Л | И | И | И | И |
| Л | Л | И | И | И |
5. При наличии времени доказать еще несколько формул на усмотрение учителя.
IV. Домашнее задание
Изучить формулы законов логики.
Урок 8
Тема. Понятие математической логики.
Решение логических задач.
Цель. Выработка навыков в преобразовании
логических выражений.
Ход урока
Решение логических задач
Операция “и” называется логическим
умножением, поэтому для большей наглядности будем
заменять ее знаком умножения. Операция “или”
называется логическим сложением, поэтому для большей
наглядности будем заменять ее знаком “+”.
Операцию “не” будем обозначать надчеркиванием, а
следование — стрелкой.
Задача 1. Перевести на язык алгебры логики
следующее высказывание: “Если будет солнечная
погода, то ребята пойдут на пляж, а если будет
пасмурная погода, то ребята пойдут в кино”.
Решение:
Введем следующие простые высказывания:
С — солнечная погода;
П — ребята пойдут на пляж;
К — ребята пойдут в кино.
Первая часть высказывания записывается
формулой (С Þ
Р), а вторая — (C Þ
К) . Оба высказывания
истинны. Если их логически перемножить, то
получим сложное высказывание, в котором связано
все, о чем говорилось в задаче (С C
Р) •( C Þ
К).
Задача 2. Найдите отрицание высказывания:
“Если урок будет интересным, то никто из
учеников — Миша, Вика, Света — не будет разговаривать”.
Решение:
Введем следующие простые высказывания:
Y — урок будет интересным;
М — Миша будет разговаривать;
В — Вика будет разговаривать;
С — Света будет разговаривать.
Тогда
Y Þ M • B • C = Y + M • B • C = Y • M • B • C = Y • (M + B + C)
Урок будет интересным, и Миша, или Вика, или Света будет разговаривать.
Задача 3. Три свидетеля дали показания, что
преступники скрылись с места преступления:
а) на черном “Бьюике”;
б) на синем “Форде”;
в) не на черном “Крайслере”
Каждый из них в чем-то одном ошибался. На
какой машине скрылись преступники?
Решение:
С — черная,
S — синяя,
B — “Бьюик”,
F — “Форд”,
К — “Крайслер”.
Ложными будут высказывания:
B • F,
F • K, B • K, S • C.
Из условия задачи истинно следующее
высказывание:
(C + B) • (S + F) • (C + K) = (C •
S + C • F + B • S + B • F) • (C+K) = ((C • F + B • S) •
C + K) = (C • F + C • B • S + B • S • K) = C • B •
S
У преступников был синий “Бьюик”.
Задача 4. Кто из школьников — Андрей,
Виктор, Света, Дима — играет в шахматы, а кто не
играет, если известно следующее:
а) если Андрей или Виктор играет, то Света
не играет;
б) если Виктор не играет, то играют Света и
Дима;
в) Света играет.
Решение:
Введем следующие простые высказывания:
А — Андрей играет в шахматы;
В — Виктор играет в шахматы;
С — Света играет в шахматы;
D — Дима играет в шахматы.
Тогда:
а) (A + B) Þ
C б) B
Þ
C • D
в) C
Запишем сложное высказывание:
((A + B) Þ
C)•(B Þ
C • D) • C = (A + B + C) • (B + C •
D) • C = (A • B + C) • (B + C • D) • C = (A
• B • B + A • B • C • D + C • B + C
• C • D) • C = (A • B • C • D + C
• B) • C = A • B • C • D + C • B •
C = A • B • C • D
Следовательно, Андрей и Виктор не играют в
шахматы, а Света и Дима играют.
Домашнее задание
Таблицы истинности логических операций.
Урок 9
Тема. Логические элементы компьютера.
Цель. Изучить логические элементы ЭВМ.
Ход урока
I. Самостоятельная работа (25 минут)
Составить таблицу истинности высказываний.
Вариант 1
Вариант 2
1) не В и(А или С)
1) В и (не А или С)
2) не А и не В и С
2) А и не В и С
Вариант 3
Вариант 4
1) не А и (В или не С)
1) не А и (не В или С)
2) не А и В и С
2) А и не В и не С
Каждая таблица должна иметь следующие
исходные данные:
| A | B | C |
| И | И | И |
| И | И | Л |
| И | Л | И |
| Л | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
| Л | Л | Л |
II. Изучение нового материала
1. Кодирование информации электрическими
сигналами.
Мы разобрались, почему информация в ЭВМ
кодируется 0 и 1, а теперь выясним, как это
реализуется. Значение двоичного числа, равного 1, часто
называют логической единицей, а число 0 называют
логическим нулем. В простейшем случае за логическую
единицу можно принять наличие напряжения в
проводе, а отсутствие напряжения — за логический ноль.
На практике поступают несколько иначе:
напряжение в проводе, равное 5 В, принимают за логическую
единицу, а напряжение около 0 В принимают за
логический ноль. Это связано с особенностями работы
электронных схем.
2. Вентили, или логические элементы ЭВМ.
В основе обработки информации
компьютером лежит алгебра логики, основоположником
которой является английский математик Дж. Буль.
Электронные схемы, реализующие различные логические
операции, называют вентилями.
Вентиль НЕ преобразует сигнал в
противоположный; если на вход элемента подана логическая
единица, то на выходе этого элемента будет логический
ноль, и наоборот.
Этот элемент схематически можно
изобразить так:
Соотношение между сигналами на входах и
выходе можно задать таблицей:
| вход | выход |
| 1 | 0 |
| 0 | 1 |
Вентиль ИЛИ преобразует два сигнала,
поданных на вход, в один сигнал на выходе по
следующему принципу: если на любой вход (или на два
одновременно) логического элемента ИЛИ будет подана
логическая единица, то на выходе элемента будет
логическая единица; если на оба входа подан логический
ноль, то на выходе элемента ИЛИ также будет ноль.
Этот элемент схематически можно
изобразить так:
Соотношение между сигналами на входах и
выходе можно задать таблицей:
| Вход 1 | Вход 2 | Выход |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Вентиль И преобразует два сигнала,
поданных на вход, в один сигнал на выходе по следующему
принципу. Если на любой вход (или оба одновременно) будет
подан логический ноль, то на выходе будет
логический ноль. Если на оба входа подана логическая
единица, то на выходе элемента И будет единица.
Этот элемент схематически можно
изобразить так:
Соотношение между сигналами на входах и
выходе можно задать таблицей:
| Вход 1 | Вход 2 | Выход |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
III. Домашнее задание
Конспект.
Урок 10
Тема. Элемент памяти “триггер”.
Цель. Изучить механизм запоминания
информации в компьютере.
Обеспечение урока. Программа “Логэл”.
Ход урока
I. Разбор самостоятельной работы (10 минут)
Вариант 1
Вариант 2
1) не В и (А или С)
1) В и (не А или С)
2) не А и не В и С
2) А и не В и С
Вариант 3
Вариант 4
1) не А и (В или не С)
1) не А и (не В или С)
2) не А и В и С
2) А и не В и не С
Решения удобно распечатать на листах и раздать по одному на парту, чтобы учащиеся сами разобрали свои ошибки. Ответить на вопросы.
Ответы по вариантам:
Вариант 1
Задача 1
| A | B | C | не B | A или C | не B и (A или С) |
| И | И | И | Л | И | Л |
| И | И | Л | Л | И | Л |
| И | Л | И | И | И | И |
| Л | И | И | Л | И | Л |
| И | Л | Л | И | И | И |
| Л | И | Л | Л | Л | Л |
| Л | Л | И | И | И | И |
| Л | Л | Л | И | Л | Л |
Задача 2
| A | B | C | не A | не B | не A и не B и С |
| И | И | И | Л | Л | Л |
| И | И | Л | Л | Л | Л |
| И | Л | И | Л | И | Л |
| Л | И | И | И | Л | Л |
| И | Л | Л | Л | И | Л |
| Л | И | Л | И | Л | Л |
| Л | Л | И | И | И | И |
| Л | Л | Л | И | И | Л |
Вариант 2
Задача 1
| A | B | C | не A | не A или C | B и (не A или С) |
| И | И | И | Л | И | И |
| И | И | Л | Л | Л | Л |
| И | Л | И | Л | И | Л |
| Л | И | И | И | И | И |
| И | Л | Л | Л | Л | Л |
| Л | И | Л | И | И | И |
| Л | Л | И | И | И | Л |
| Л | Л | Л | И | И | Л |
Задача 2
| A | B | C | не B | A и не B и C |
| И | И | И | Л | Л |
| И | И | Л | Л | Л |
| И | Л | И | И | И |
| Л | И | И | Л | Л |
| И | Л | Л | И | Л |
| Л | И | Л | Л | Л |
| Л | Л | И | И | Л |
| Л | Л | Л | И | Л |
Вариант 3
Задача 1
| A | B | C | не C | не A | B или не С | не А и (В или не C) |
| И | И | И | Л | Л | И | Л |
| И | И | Л | И | Л | И | Л |
| И | Л | И | Л | Л | Л | Л |
| Л | И | И | Л | И | И | И |
| И | Л | Л | И | Л | И | Л |
| Л | И | Л | И | И | И | И |
| Л | Л | И | Л | И | Л | Л |
| Л | Л | Л | И | И | И | И |
Задача 2
| A | B | C | не A | не A и B и C |
| И | И | И | Л | Л |
| И | И | Л | Л | Л |
| И | Л | И | Л | И |
| Л | И | И | И | И |
| И | Л | Л | Л | Л |
| Л | И | Л | И | Л |
| Л | Л | И | И | Л |
| Л | Л | Л | И | Л |
Вариант 4
Задача 1
| A | B | C | не A | не B | не B илиС | не А и (не В или C) |
| И | И | И | Л | Л | И | Л |
| И | И | Л | Л | Л | Л | Л |
| И | Л | И | Л | И | И | Л |
| Л | И | И | И | Л | И | И |
| И | Л | Л | Л | И | И | Л |
| Л | И | Л | И | Л | Л | Л |
| Л | Л | И | И | И | И | И |
| Л | Л | Л | И | И | И | И |
Задача 2
| A | B | C | не B | не C | A и не B и не С |
| И | И | И | Л | И | Л |
| И | И | Л | Л | Л | Л |
| И | Л | И | Л | И | Л |
| Л | И | И | И | И | Л |
| И | Л | Л | Л | Л | И |
| Л | И | Л | И | И | Л |
| Л | Л | И | И | И | Л |
| Л | Л | Л | И | И | Л |
II. Повторение изученного материала
1. Фронтальный опрос:
а) из каких электронных приборов
создаются вентили;
б) какие три основных логических элемента
вы знаете;
в) как работает вентиль НЕ;
г) как работает вентиль И;
д) как работает вентиль ИЛИ;
е) как назвать вентили, изображенные на
доске, и как они работают?
Ответ: ИЛИ-НЕ, И-НЕ.
Если на входе элемента ИЛИ-НЕ есть хотя бы
одна 1, то на выходе будет 0.
Если на входе элемента И-НЕ есть хотя бы
один 0, то на выходе будет 1.
Эти же вентили в виде схем изображаются
следующим образом:
2. Тестирование.
С помощью программы “Логэл” провести
оценку знаний.
III. Изучение нового материала
1. Элемент памяти “триггер”.
Триггер — элемент оперативной памяти
компьютера, способный запомнить и сохранить один
бит информации.
Триггер был изобретен в 1918 г. М.А. Бонч-Бруевичем, руководителем Нижегородской
лаборатории связи.
Триггер имеет два устойчивых состояния, в
которые он поочередно переходит под воздействием
входных сигналов при записи информации.
Существует множество типов триггеров. Один из них, так
называемый RS-триггер, построен на двух элементах ИЛИ-НЕ.
Рассмотреть работу RS-триггера, результаты
занести в таблицу.
| Вход S | Вход R | Выход Q | Выход P |
| 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 |
Вход R называют входом установки триггера в нулевое состояние, а вход S — в единичное. Триггер имеет два выхода: Q — прямой выход, P — инверсный.
Задача. Оперативная память компьютера — 32 Мб. Сколько триггеров она содержит?
Решение:
Представим 32 Мб в виде 2N : 32 Мб = 25
• 210 Кб = 25 • 210 • 210 байт =
= 25 • 210 • 210 • 28 бит = 232 .
Следовательно, требуется 232 триггеров.
IV. Домашнее задание
Конспект.
Урок 11
Тема. Одноразрядный сумматор.
Цель. Изучить механизм двоичного сложения
в компьютере.
Обеспечение урока. Программа “Сумматор”.
Ход урока
I. Повторение ранее изученного материала
1. Вызвать к доске учащегося и дать задание:
“Начертить схему триггера и рассказать о его
работе”.
2. Фронтальный опрос по вопросам
предыдущих уроков:
а) что такое вентили;
б) какие три основных вентиля вы знаете;
в) как работает вентиль НЕ;
г) как работает вентиль И;
д) как работает вентиль ИЛИ;
е) как работает вентиль И-НЕ;
ж) как работает вентиль ИЛИ-НЕ?
II. Изучение нового материала
1. Одноразрядный сумматор. Рассмотреть
схему работы сумматора, результаты занести в
таблицу.
На схеме использованы следующие
обозначения:
В1 (вход 1) — первый операнд (слагаемое);
В2 (вход 2) — второй операнд операции
сложения;
Пi — признак переноса 1 из предыдущего
разряда;
Пi+1 — признак, указывающий, будет ли
осуществлен перенос в следующий разряд после
выполнения операции сложения.
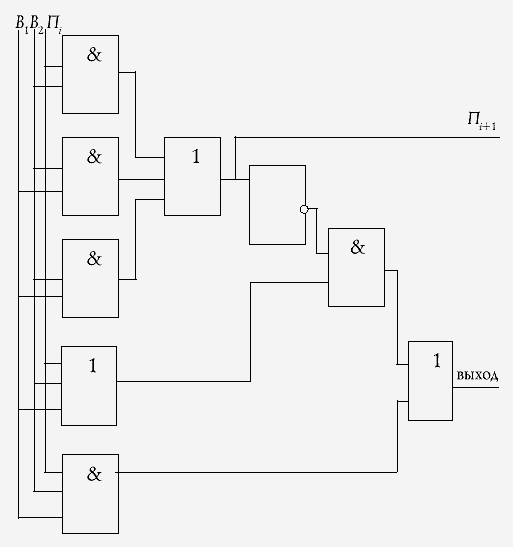
| Вход 1 | Вход 2 | Перенос 1 | Перенос 2 | Выход |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
2. Проверка усвоения изученного материала с использованием программы “Сумматор”.