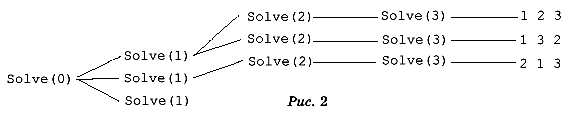Вы - -й посетитель этой странички 

Основы программирования

С.М. Окулов, г. Киров

Занятие 13. Рекурсия     План занятия     · понятие рекурсии;     · короткие примеры для иллюстрации рекурсии;     · экспериментальная работа с программами перечисления всех последовательностей длины n из чисел от 1 до k; генерации перестановок чисел от 1 до n; перечисления всех разбиений числа n на сумму слагаемых n = a1 + a2 + … + ak , где k, a1 , a2 , …, ak > 0;     · выполнение самостоятельной работы. Понятие рекурсии     Рекурсией называется ситуация, когда процедура или функция вызывает сама себя. Типичная рекурсивная процедура имеет вид: Procedure Rec(t:Integer);     Begin         <действия на входе в рекурсию>;         If <проверка условия> Then Rec(t-1);         <действия на выходе из рекурсии>     End; Проиллюстрируем рисунком последовательность рекурсивных вызовов на примере функции вычисления факториала числа. Function Factorial(n: Integer): LongInt; Begin     If n=1 Then Factorial:=1     Else Factorial:=n*Factorial(n-1) End;     На рис. 1 показаны прямой (тонкая линия) и обратный ход рекурсии. Обратите внимание на то, что в любой рекурсивной подпрограмме обязательно должна быть нерекурсивная ветвь (в нашем случае это If n=1 Then Factorial:=1).     При выполнении рекурсивных подпрограмм используется специальная область памяти, называемая “стеком возвратов”. В нем запоминаются адреса точек возврата и значения локальных переменных.     Пусть переменной а присваивается значение 5!:

Таким образом,
a : = Factorial( 5 ) = 5 •Factorial ( 4 ) = 5•4•Factorial(3) = 5•4•3•Factorial(2) = 5•4•3•2•Factorial(1) = 5•4•3•2•1

    Приведем несколько коротких примеров рекурсивных функций и процедур.
    1. Сложение двух чисел a + b. Запишем рекурсивное определение операции сложения двух чисел:

		a, если b=0
a + b = (1)		(a+1)+(b-1), если b>0
		(a-1)+(b+1), если b<0

 Function Sum(a, b: Integer): Integer;
    Begin
        If b=0 Then Sum:=a
        Else If b>0 Then Sum:=Sum(a+1, b-1)
                Else Sum:=Sum(a-1, b+1)
    End;

    2. Печать двоичного представления натурального числа.

Procedure Rec(n: Integer );
Begin
    If n>1 Then Rec(n Div 2);
    Write(n Mod 2)
End;

    Как изменится процедура, если потребуется напечатать восьмеричное представление числа?
    3. Определить, является ли заданное натуральное число простым.
    Сформулируем задачу по-другому. Пусть требуется определить, верно ли, что заданное натуральное число n не делится ни на одно число, большее или равное m, но меньшее n. При этом значения m находятся в промежутке от 2 до n.
    Утверждение истинно в двух случаях:
    · если m = n;
    · если n не делится на m и истинно утверждение для чисел от m + 1 до n — 1.

Function Simple(m,n: Integer): Boolean;
Begin
    If m=n Then Simple:=True
    Else Simple:=(n Mod m<>0) And Simple(m+1,n)
End;

    Первый вызов функции имеет вид Simple(2,n), где n — проверяемое число.
    4. Дано натуральное число n ³ 1. Определить число a, для которого выполняется неравенство: 2^а—1 £n< 2^a. Зависимость:

а(n) =		1, n=1, если n=1 или n=2
		a(n div 2) + 1, n>1, если n>2

Function a( n: Integer): Integer;
Begin
    If n=1 Then a:=1 Else a:=a(n Div 2)+1
End;

    5. Для вычисления наибольшего общего делителя двух чисел также можно использовать рекурсивную функцию.

Function Nod(a,b:Integer):Integer;
    Begin
        If (a=0) or (b=0) Then Nod:=a+b
        Else If a>b Then Nod:=Nod(a-b,b)
            Else Nod:=Nod(a,b-a)
    End;

    6. Нахождение максимального элемента в глобальном массиве A.

Procedure Search_Max(n:Integer; Var x:Integer);
    Begin
        If n=1 Then x:=A[1]
        Else Begin
                Search_Max(n-1,x);
                If A[n]>x Then x:=A[n]
               End
    End;

    7. Возведение целого числа a в целую неотрицательную степень n.

Function Pow(a,n:Integer):Integer;
    Begin
        If n=0 Then Pow:=1
        Else If n Mod 2=0 Then Pow:=Pow(a*2,n Div 2)
            Else Pow:=Pow(a,n-1)*a
    End;

    8. Процедура ввода с клавиатуры последовательности чисел (окончание ввода — число 0) и вывода ее на экран в обратном порядке имеет вид:

Procedure Solve;
    Var n:Integer;
    Begin
        ReadLn(n);
        If n<>0 Then Solve;
        Write(n:5)
    End;

    9. Каждое число Фибоначчи начиная с третьего равно сумме двух предыдущих чисел, а первые два равны 1 (1, 1, 2, 3, 5, 8, 13, 21, ...). В общем виде n-е число Фибоначчи можно определить так:

Ф(n)=		1, если n = 1 или n = 2
		Ф(n-1) + Ф(n-2), если n > 2

Function Fib(n:Integer):Integer;
    Begin
        If n<=2 Then Fib:=1
            Else Fib:=Fib(n-1)+Fib(n-2)
    End;

    10. Найти сумму первых n членов арифметической (геометрической) прогрессии.
    Арифметическая прогрессия определяется тремя параметрами: первым элементом a, разностью между соседними элементами d и количеством членов прогрессии n. Очередной элемент прогрессии вычисляется по предыдущему прибавлением разности — a_новое :=a_старое + d.

Function Sa(n,a:Integer):Integer;
    Begin
        If n>0 Then Sa:=a+Sa(n-1,a+d)
        Else Sa:=0
    End;

    Примечание. Попробуйте убрать ветвь Else и объяснить полученный результат.

    Для приведенных примеров нарисуйте схемы работы процедур и функций для конкретных входных данных (естественно, не очень больших). 

Экспериментальный раздел занятия

    1. Даны натуральные числа n и k. Перечислить все последовательности длины n из чисел от 1 до k.
    Количество таких последовательностей — kⁿ, (Действительно, на каждое из n мест разрешается записывать числа от 1 до k, перемножаем и получаем результат. Строгое доказательство осуществляется традиционно, с помощью простой индуктивной схемы.) Пусть n = 3, k = 2 и последовательности выводятся в следующем порядке: 1 1 1, 1 1 2, 1 2 1, 1 2 2, 2 1 1, 2 1 2, 2 2 1, 2 2 2. Чем он (порядок) характеризуется? Возьмем две соседние последовательности, например, 1 1 2 и 1 2 1. До какой-то позиции они совпадают, в данном случае до второй (несовпадение возможно и в первой позиции), а в этой позиции число во второй последовательности больше, чем число в первой последовательности. Такой порядок называется лексикографическим. Как из очередной последовательности получать следующую в лексикографическом порядке? Просматриваем очередную последовательность справа налево. Находим первый элемент, не равный k. Увеличиваем его на единицу, а “хвост” последовательности максимально “уменьшаем”, т.е. записываем в него 1. В последней последовательности сделать такое преобразование, естественно, не представляется возможным.

    Примечание. Разумеется, сейчас самое время потренироваться на примерах. Как вы поняли постановку задачи?

    Для хранения последовательности будем использовать одномерный массив из n элементов. Элементами массива являются целые числа в диапазоне от 1 до k. Явно отразим это в описании, вместо типа Integer воспользуемся ограниченным типом 1..k: Type MyArray = Array[1..n] Of 1..k;. Напишем “костяк” программы и очевидную процедуру вывода элементов массива.

{$R+}
Program My13_1;
    Const n=3;
    k=2;
    Type MyArray=Array[1..n] Of 1..k;
    Var A:MyArray;
    Procedure Print;
        Var i:Integer;
        Begin
            For i:=1 To n Do Write(A[i]:3);
            WriteLn
        End;
    Procedure Solve(t:Integer);
        Begin
        End;
    Begin
        FillChar(A,SizeOf(A),1)
        Solve(1)
    End.

    Что определяет параметр рекурсии t? Позицию в последовательности (номер элемента в массиве A). При значении t, большем n, необходимо вывести очередную последовательность, а иначе — записать очередной элемент, он определяется значением управляющей переменной i в позицию t.

Procedure Solve(t:Integer);
    Var i:Integer;
    Begin
        If t>n Then Print
        Else For i:=1 To k Do Begin
                A[t]:=i;
                Solve(t+1)
               End
    End;

    Измените программу так, чтобы последовательности выводились в следующей очередности: 2 2 2, 2 2 1, 2 1 2, 2 1 1, 1 2 2, 1 2 1, 1 1 2, 1 1 1.
    Предположим, что значение k больше n. Измените программу. Теперь i-й элемент последовательности не должен превосходить i. Пусть теперь при этом же предположении (k > n) требуется сгенерировать возрастающие последовательности чисел. На месте t в последовательности допускается запись чисел из интервала от A[t — 1] + 1 до k — (n — t). Действительно, при t = n максимальное число в позиции n равно, естественно, k; при t = n — 1 максимальное число в позиции n — 1 есть k — 1 и т.д. Эта мысль приводит к следующему изменению процедуры Solve:

Procedure Solve(t:Integer);
    Var i:Integer;
    Begin
        If t>n Then Print
            Else For i:=A[t-1]+1 To k-n+t Do Begin
                     A[t]:=i;
                     Solve(t+1)
                   End
    End;

    Однако только этим изменением в программе ограничиться нельзя. Первый вызов процедуры Solve(1) приводит к знакомой ошибке Error 201: Range check error в строке For i:=A[t-1]+1 To k-n+t Do. Причина очевидна — выход индекса за пределы массива A. Изменим описание типа на

Type MyArray =Array[0..n] Of 1..k;.

    Программа выдает результат, но содержит логическую неточность. При первом вызове Solve используется неопределенное значение A[t — 1]. При изменении первого вызова на A[0]:=0; Solve(1); возникает новая ошибка: Error 76: Constant out of range (значение константы выходит за допустимый диапазон). Еще одно изменение: Type MyArray=Array[0..n] Of 0..k;, — и можно в первом приближении закончить эксперименты с программой.
    2. С перестановками мы познакомились на предыдущем занятии. Напишем рекурсивную процедуру генерации перестановок чисел от 1 до n.
    В чем здесь суть рекурсии? Фиксируем на первом месте очередное число и генерируем все перестановки этого вида. При этом поступаем точно по такой же схеме. Фиксируем число на втором месте и генерируем все перестановки уже с фиксированными элементами на первом и втором местах. Пусть n = 3. Перестановки должны генерироваться в следующей последовательности: 1 2 3, 1 3 2, 2 1 3, 2 3 1, 3 2 1, 3 1 2. Пусть n = 4. Вместо многоточия запишите генерируемые перестановки 1 2 3 ..n] Of Integer;
    Var A:MyArray;
             i:Integer;
    Procedure Swap(Var a,b:Integer);
        Var c:Integer;
        Begin c:=a;a:=b;b:=c End;
    Procedure Solve(t:Integer);
        Var i:Integer;
        Begin
            If t>=n Then Print
                Else For i:=t+1 To n Do Begin
                         Swap(A[t+1],A[i]);
                         Solve(t+1);
                         Swap(A[t+1],A[i])
                       End
        End;
    Begin
        For i:=1 To n Do A[i]:=i;
        {Первая перестановка – 1 2 3 … n.}
        Solve(0){Первый вызов.}
    End.

Для простоты будем считать, что каждый рекурсивный вызов приводит к созданию “копии” процедуры. (Это не так, но нам легче при этом предположении формулировать вопросы.) Сколько “копий” процедуры Solve создается при n = 3? Сколько раз создаются копии с t = 2? Сколько выполняется лишних обменов вида A[j] « A[j]? На рис. 2 приводится часть схемы вызовов процедуры Solve при n = 3. Для ответа на формулированные вопросы закончите этот рисунок.

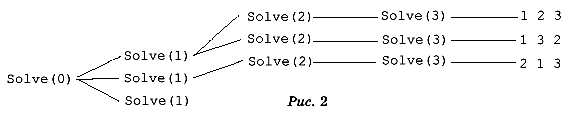
    Измените описание типа элементов массива A на Type MyArray=Array[1..n] Of 1..n;. Теперь при вызове процедуры Swap возникает ошибка: Error 26: Type mismatch. Устраните ее.
    3. Дано натуральное число n. Необходимо получить все разбиения числа n на сумму слагаемых n = a₁ + a₂ + … + ak , где k, a₁ , a₂ , …, a_k > 0.
    Будем считать разбиения эквивалентными, если суммы отличаются только порядком слагаемых. Множество эквивалентных сумм представляем последовательностью a ₁ , a ₂ , …, a _k , где a₁ ³ a₂ ³ … ³ a_k . При n = 4 разбиения 1 + 1 + 1 + 1, 2 + 1 + 1, 2 + 2, 3 + 1, 4 перечислены в лексикографическом порядке. Для каждой пары соседних разбиений находится номер позиции, в которой число из второго разбиения больше числа из первого разбиения, а до этой позиции последовательности совпадают. Будем генерировать разбиение в порядке, обратном лексикографическому: 4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1. Рекурсивная схема реализации просматривается достаточно легко. Пусть мы записали в позицию t число a_t , сумма чисел a₁ + a₂ + … +a_t = s. С позиции t + 1 мы генерируем все разбиения числа n — s, причем для элемента A[t + 1] (и остальных) должно выполняться неравенство A[t + 1] £ A[t]. Переход к следующему разбиению в позиции t сводится, если это возможно, к вычитанию 1.
    Уточним некоторые технические детали. Разбиение хранится в глобальном массиве A. Количество элементов в разбиении различно. Значение переменной t определяет текущий размер выводимой части массива A. Соответственно, изменим процедуру Print.

Procedure Print(t:Integer);
    Var i:Integer;
    Begin
        For i:=1 To t Do Write(A[i]:3);
        WriteLn
    End;

    Рекурсивная процедура Solve имеет два параметра: число n и позицию t, начиная с которой необходимо получить все разбиения числа n. Первым разбиением является разбиение, соответствующее записи числа n в позицию t, а затем… Последовательно записываем в позицию t числа n—1, n—2, …, и так до 1, а с позиции t + 1 генерируем все разбиения чисел 1, 2, …, n—1 соответственно. Приведем текст решения.

{$R+}
Program My13_3;
    Const n=4;
    Type MyArray=Array[1..n] Of Integer;
    Var A:MyArray;
Procedure Solve(n,t:Integer)
    Var i:Integer;
    Begin
        If n=1 Then Begin A[t]:=1;Print(t) End
            Else Begin A[t]:=n;Print(t);
                     For i:=1 To n-1 Do Begin
                     A[t]:=n-i;
                     Solve(i,t+1)
                   End
            End
    End;
Begin
    Solve(n,1);
    ReadLn
End.

    Однако после запуска программы получается результат, несколько отличный от предполагаемого: 4, 3 1, 2 2, 2 1 1, 1 3, 1 2 1, 1 1 2, 1 1 1 1.
    Разбиения 1 3, 1 2 1 и 1 1 2 — лишние. Изменим процедуру:

Procedure Solve(n,t:Integer);
    Var i:Integer;
    Begin
        If n=1 Then Begin A[t]:=1;Print(t) End
            Else Begin
            If n<=A[t-1] Then Begin
                A[t]:=n; Print(t) End;
                    For i:=1 To n-1 Do Begin
                        A[t]:=n-i;
                        Solve(i,t+1)
                    End
                   End
    End;

    Появление индекса t — 1 требует изменить описание типа массива на Type MyArray=Array[0..n] Of Integer; и осуществлять начальное присвоение A[0]:= n перед первым вызовом Solve(n,1). Если этого не сделать, возникает известная ошибка: Error 201: Range check error. Что мы пытались сделать? Отсечь лишние разбиения при их выводе, но не при генерации! Запуск программы нас в очередной раз разочарует. Результат работы: 4, 3 1, 2 2, 2 1 1, 1 2 1, 1 1 1 1. Изменим процедуру.

Procedure Solve(n,t:Integer);
    Var i,q:Integer;
    Begin
        If n=1 Then Begin A[t]:=1;Print(t) End
        Else Begin
        If n<=A[t-1] Then Begin
           A[t]:=n; Print(t) End;
            q:=Min(n-1,A[t-1]);
            For i:=q DownTo 1 Do Begin
                A[t]:=i;
                Solve(n-i,t+1)
                End
            End
    End;

    Нам потребуется функция Min:

Function Min(a,b:Integer):Integer;
Begin
    If a<b Then Min:=a Else Min:=b
End;

    Получаем правильный результат: 4, 3 1, 2 2, 2 1 1, 1 1 1 1, — но часть решений мы по-прежнему “отсекаем” только на выходе. Продолжите исследование. Научитесь выводить разбиения в следующих порядках:
    · 1 1 1 1, 2 1 1, 2 2, 3 1, 4;
    · 1 1 1 1, 1 1 2, 1 3, 2 2, 4;
    · 4, 2 2, 1 3, 1 1 2, 1 1 1 1.

Задания для самостоятельной работы

    1. Написать рекурсивную программу вывода на экран следующей картинки:

    2. Условие задачи “Ханойские башни” хорошо известно. Приведем программу, которая печатает последовательность переноса колец посредством рекурсивной процедуры MoveTown.

Program My13_z1;
    Var n: Integer;
    Procedure MoveTown(High,FromI,ToI,WorkI: Integer);
        Begin
            If High>0 Then Begin
                MoveTown(High-1,FromI,WorkI,ToI);
                Writeln('Перенести кольцо №',High,' со стержня ',FromI,' на стержень ',ToI);
                MoveTown(High-1,WorkI,ToI,FromI)
            End
        End;
    Begin
        Write('Количество колец = ');
        ReadLn(n);
        MoveTown(n,1,3,2)
    End.

    Данная задача своим происхождением обязана легенде, в которой рассказывается, что в большом храме Бенареса на бронзовой плите установлены три алмазных стержня, на один из которых Бог нанизал во время сотворения мира 64 золотых диска. С тех пор день и ночь монахи, сменяя друг друга, каждую секунду перекладывают по одному диску согласно известным правилам. Конец света наступит тогда, когда все 64 диска будут перемещены, на что потребуется чуть больше 58 млрд лет.
    3. Составить рекурсивную функцию вычисления значения функции Аккермана для неотрицательных чисел n и m, вводимых с клавиатуры.

A(n, m)=		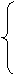m+1, n = 0
		A(n-1, 1), n ¹ 0, m = 0
		A(n-1, A(n, m-1)), n > 0, m > 0

    Найдите одну пару значений n и m, при которых возникнет переполнение стека адресов возврата.

    4. Функция F(n) определена для целых положительных чисел следующим образом:

F(n) =		1,                если n = 1
			F(n div i), если n ³ 2

    Соответствует ли приведенная ниже функция данному определению?

Function F(n:Integer):Integer;
    Var i,s:Integer;
    Begin
        If n=1 Then s:=1
            Else For i:=2 To n Do
                    s:=s+F(n Div 2);
        F:=s
    End;

    Какие значения возвращает данная функция при n = 5, 6, 7, ..., 20?
    5. Число сочетаний C(n, m) вычисляется по формуле C(n, m) = C(n—1, m—1) + C(n—1, m), при этом C(n, 0) = 1 и C(n, n) = 1. Напишите рекурсивную функцию для подсчета числа сочетаний. Определите область ее применения (диапазон допустимых значений n и m).