
Вы - -й посетитель этой странички
Олимпиады по информатике
В.Н. Пинаев
Вниманию читателей предлагаются задачи
теоретических и практических туров
рыбинских городских школьных олимпиад,
чемпионатов и конкурсов по информатике, а
также методические рекомендации
составителям и организаторам олимпиад. Все
задачи теоретических туров снабжены
полными решениями. Для задач практических
туров показаны ключевые идеи их решений.
Для некоторых задач приведены полные
тексты программ. Рассказано об опыте
проведения молодежных чемпионатов по
информатике и программированию. Кроме того,
в работе обсуждаются теоретические вопросы
роли интуиции при решении заданий по
информатике и многое другое. Часть
материалов ранее публиковалась автором.
Так, материалы рыбинских чемпионатов
освещались в газете “Информатика”.
Данный материал предназначен
учителям и преподавателям вузов для
подготовки и проведения творческих
состязаний по информатике и
программированию, а также может
использоваться учащимися старших классов и
студентами младших курсов вузов,
изучающими основы программирования.
От автора
С 1975-го по 1983 год я обучался на
математикомеханическом факультете
Ленинградского, а ныне Санкт-Петербургского
государственного университета. Я поступил
на отделение механики, но после первого
курса перевелся на отделение кибернетики.
Причиной этого стали мои университетские
преподаватели, показавшие мне чудесный мир
программирования, в котором одной лишней
запятой можно нарушить гармонию; мир, в
котором совершенной признается не та
программа, в которую нечего добавить, а та,
из которой выброшено все лишнее.
На отделении кибернетики я
выбрал кафедру математического и
программного обеспечения ЭВМ, которую и
закончил в 1980 году. Потом были три года
аспирантуры, а затем распределение на
работу в Рыбинск.
Помню, как одна из первых моих
программ, написанная на языке Алгол-60, была
“арестована”, так как при ее работе на АЦПУ-128
(АЦПУ-128 — алфавитно-цифровое печатающее
устройство с выводом в одну строку до 128
символов) в одну колонку выводились все
простые числа в диапазоне от 2 до 1 000 000.
Оператор ЭВМ был вынужден “снять” задание,
которому, судя по всему, для полного вывода
ответов потребовался бы недельный запас
бумаги!
Потом была вереница языков: Рефал,
Ассемблер, PL/1, Алгол-68, Фортран, Бейсик,
Паскаль, Пролог, Лисп — и другие. И в каждом
языке были свои прелести, свои изюминки.
Но самое интересное — это когда
непонятная задача превращалась в
элегантную программу, когда из
примитивного подбора ответов возникал
изящный алгоритм. Иногда на поиск решения
уходили годы, как было у меня в случае с
написанием интроспективной программы. Я
узнал об этой задаче ( Интроспективная
программа — программа, которая во время
исполнения выводит на экран свой
собственный текст. Пользоваться для этой
цели хранящейся на диске копией текста
запрещено. Полное условие задачи
опубликовано в книге Ч.Уэзерелла “Этюды
для программистов”.), будучи еще
аспирантом, а первое решение нашел уже
здесь, в Рыбинске.
Через несколько лет мне довелось
навестить alma mater. И помню, как на одном из
стендов я увидел чьюто прикрепленную
распечатку (Распечатка (листинг программы)
— текст программы, выведенный на
печатающее устройство.) с рукописным
текстом поверх: “Она печатает сама себя!”.
Вот таким увлекающимся людям и
предназначен этот материал.
Введение
Олимпиадной подготовке по
информатике уделяется в литературе
достаточно много внимания [1—5]. Каждая
олимпиада — это не только творческое, но и
спортивное состязание со своими призерами
и аутсайдерами, восторгами и переживаниями,
идеями и ошибками [6, 7]. Существует
устойчивое и, с нашей точки зрения,
оправданное мнение, что олимпиады по
информатике — это не сама школьная
информатика, как большой спорт — это не
уроки физкультуры. Но полноводная река
питается ручейками и родниками. На
сегодняшний день олимпиады по информатике
показывают уровень, на который мы, школьные
учителя, можем и должны поднимать планку
сложности наших ежедневных занятий.
Не стоит забывать и о том, что
эстафету школьников в олимпиадном движении
подхватывают студенты [8]. Под эгидой
известной компьютерной организации ACM (Association
for Computing Machinery) вот уже более двадцати лет
проводятся чемпионаты по программированию
среди студентов. Схема соревнований в общих
чертах такова: в различных регионах планеты
одновременно проводятся полуфинальные
соревнования, победители которых
собираются ежегодно в феврале — марте для
участия в финальной части чемпионата.
Обычно финал проходил на территории США, но
в 1999 году соревнования впервые состоялись в
Европе (Эйндховен, Голландия).
В 2000 году впервые чемпионами мира
стали студенты Санкт-Петербургского
государственного университета.
По правилам проведения
чемпионатов мира все задачи формулируются
на английском языке. К сожалению, этот
фактор сыграл свою отрицательную роль: семь
российских команд, принимавших участие в
четвертьфинале Северо-Восточной
европейской зоны в 2000 году, проходившем в
Рыбинске, за пять часов не успели решить ни
одной задачи. Но для лучших команд это не
представляло особых проблем. Ведущий вуз
страны Московский государственный
университет — выставил для участия в
четвертьфинале четыре (!) команды. Эти, без
сомнения, элитные команды заняли четыре
места в первой пятерке. Первая команда МГУ,
занявшая первое место, увезла с собой
главный приз — компьютер Pentium III, который
предоставил наш генеральный спонсор — ОАО
“Рыбинские моторы”.
Автор данной публикации
занимается подготовкой и проведением
олимпиад и конкурсов по информатике около
пятнадцати лет. Все это время он наряду с
проведением самих олимпиад и конкурсов в
обязательном порядке осуществляет разбор
задач.
Форма проведения олимпиады по
информатике может быть различна. В
последнее время многие регионы практикуют
проведение одного или нескольких
практических туров. Фактически олимпиада
по информатике превращается в олимпиаду по
программированию, хотя в школьном
образовании нет такого предмета! Именно
поэтому на методическом совете учителей
информатики Рыбинского муниципального
округа был принят регламент школьной
олимпиады, которая названа Олимпиадой по
информатике.
Подбор заданий олимпиады крайне
важен. Нужны не просто сложные задачи, а
разносторонние задания, которые были бы
одновременно интересны, поучительны и
познавательны для большинства участников.
Работа по подготовке олимпиады
предполагает проработку методики будущего
оценивания ожидаемых решений. Однако
проведение только практического тура
олимпиады не позволяет выявить частичные
решения или интересные идеи этих решений.
Выявление особенностей представленного
решения подбором специальных тестов
позволяет оценить качество только
законченного решения. Кроме того, если
учащийся нашел интересную идею, это не
означает, что он успеет или сможет ее
реализовать во время практического тура.
Автор считает, что главное в информатике —
это не работающая программа, а общая
проработка задачи, которая включает в себя
построение формальной модели и ее
исследование. Именно здесь в наибольшей
степени проявляется творческий потенциал
учащихся.
Вот как видятся автору главные
цели проведения олимпиад по информатике:
· развитие
творческих способностей учащихся,
· повышение
интереса учащихся к изучению информатики,
·
формирование умения решать нестандартные
задачи,
·
приобретение и совершенствование
практических навыков и умений,
· выявление
одаренных учащихся,
· активизация
всех форм внеклассной и внешкольной работы
с учащимися,
· оказание
помощи учащимся старших классов в выборе
профессии,
· расширение
знаний учащихся о предмете.
Зачастую конкурсы и олимпиады
носят явно выраженный спортивный или
состязательный характер. Хотя это и
интересно, тем не менее не может служить
самоцелью и быть единственным движущим
фактором.
По-видимому, целесообразно
расширять формы олимпиадного движения и
организовывать как классические олимпиады,
так и конференции, конкурсы и чемпионаты.
Роль интуиции в решении олимпиадных задач по информатике
В литературе по современным концепциям
творчества и одаренности [12—16] говорится о
знании особого типа, которое может быть
названо интуитивным, илыи имплицитным.
Главной его характеристикой является то,
что оно может быть основой только
практического действия. Такое знание
порождается, как считают некоторые ученые,
при необходимом условии практического его
применения.
Интуитивное знание, накопленное
при практической работе в некоторых
условиях, может оказаться непригодным при
изменении условий. При возникновении
некоторой проблемы человек сначала
пытается найти решение на основе
логического анализа предметной области и
применении готовых схем. Если на вербальном
уровне решение не найдено, то человек
пытается привлечь свое интуитивное знание.
На уровне интуиции каждого
человека зафиксированы такие отношения и
факты, которые логически не связаны с его
вербальным уровнем знания. Если на основе
интуитивного знания найдено верное решение,
то очень важно закрепить это решение
логическим оформлением. Тогда интуитивное
знание становится эксплицитным, или
селективным. Таким образом, знание
приобретает вербальную форму и доступно в
последующем даже при существенном
изменении начальных условий.
Именно с таких теоретических
позиций, наверное, следует подходить к роли
интуиции при решении олимпиадных задач. При
этом следует четко разделять теоретические
и практические задания олимпиады.
При решении теоретических задач
учащийся может высказать какое-либо
предположение интуитивно, и проверяющий
должен оценить его значимость.
При решении практических задач
ситуация иная. Практическая реализация
олимпиадной задачи обязана быть
законченной. В противном случае
незаконченное решение либо просто не будет
компилироваться, либо будет формировать
неверный ответ.
Если на практическом туре
учащийся высказал и реализовал некоторое
предположение, основанное на имплицитном
знании, но задача не прошла все тесты (и тем
самым не засчитана), то интуитивно верное
решение останется незакрепленным, так как
на практическом туре олимпиады не принято
анализировать решение.
Так как в большинстве случаев
предлагаемые на олимпиадах задачи не
являются стандартными, то во многих случаях
эти задачи не могут быть решены на
вербальном уровне, поэтому учащиеся
вынуждены прибегать к интуитивному уровню.
Следовательно, после олимпиады необходимо
закрепить новые знания в вербальной форме.
Для этого необходимо в обязательном
порядке провести разбор заданий олимпиады
с учащимися. Более того, такой же разбор,
включая методику оценивания, целесообразно
организовать и для учителей.
Рыбинские городские школьные олимпиады по информатике
ЗАДАЧИ ТЕОРЕТИЧЕСКИХ ТУРОВ
1. Алгоритм (2 + 3 = 5 баллов) (Общий балл за задачу представляет собой сумму баллов за отдельные вопросы (в данной задаче — “определите назначение алгоритма” и “докажите”).)
Ниже приведена запись одного и
того же алгоритма на школьном
алгоритмическом языке и на языке Паскаль.
Алгоритм (процедура) Move вызывается с
аргументом k: 0 £
k £
n.
Определите назначение алгоритма
Move и строго докажите, что данный алгоритм
делает именно это.
Школьный алгоритмический язык
алг Move (арг цел n, цел таб
x[1:n], цел k, рез цел таб x[1:n])
алг Reverse (цел i, j)
нач
цел p, t
для p от i до
(i+j) div 2
нц
t := x[p];
x[p] := x[j-p+i];
x[j-p+i] := t
кц
кон
нач
Reverse(1, n);
Reverse(k+1, n);
Reverse(1, k)
кон
Язык Паскаль
{Var x: array[1..n] of integer
- глобально определенный массив}
Procedure Move (k : integer);
Procedure Reverse (i, j :integer);
Var p, t : integer;
Begin
for p:=i to (i+j) div 2 do
begin
t := x[p];
x[p] := x[j-p+i];
x[j-p+i] := t
end
End;
Begin
Reverse(1, n);
Reverse(k+1, n);
Reverse(1, k)
End;
2. Таблица (2 балла)
Пусть имеется бесконечная
числовая таблица. Во все клетки таблицы
записано число 0. После этого в одну из
клеток таблицы записали число 1.
Опишите алгоритм отыскания
координат клетки с числом 1.
| 1 | 2 | 3 | 4 | ... | |
| 1 | 0 | 0 | 0 | 0 | ... |
| 2 | 0 | 0 | 0 | 0 | ... |
| 3 | 0 | 0 | 0 | 0 | ... |
| 4 | 0 | 0 | 0 | 0 | ... |
| ... | ... | ... | ... | ... | ... |
3. Последовательность (2 + 5 = 7 баллов)
Ученик Ваня Петров, выполняя
домашнюю работу, написал алгоритм,
определяющий некоторую конечную
последовательность. Эта
последовательность строится по любому
натуральному числу n.
1. Ввести некоторое натуральное
число n.
2. Если n = 1, то закончить
работу.
3. Если n — четное число, то
заменить n на n/2, иначе заменить n
на n + k.
4. Перейти к пункту 2.
К сожалению, Ваня забыл, чему
равняется положительная целая константа k.
Определите и докажите, при каких
значениях константы k описанный выше
алгоритм конечен при любых значениях n.
4. Оклеивание лабиринта (3 балла)
Пусть имеется прямоугольный
лабиринт, разбитый на клетки со стороной 1
метр. Длина лабиринта — n метров, ширина
— m метров. На плане лабиринта
закрашенная клетка соответствует
непроходимому препятствию. Высота
лабиринта всюду одинакова и равна 3 (трем)
метрам. Вход в лабиринт и выход всегда
размещены в левом верхнем и правом нижнем
углах. Нумерация клеток начинается из
левого верхнего угла.
Перед открытием сезона
необходимо оклеить все внутренние стены
лабиринта новыми обоями.
Опишите алгоритм определения
общей площади всех внутренних стен
лабиринта.
Входные данные
n, m; двухмерный массив (прямоугольная
таблица) размерностью n ´
m.
Элементы массива принимают одно
из двух значений: “пусто” или “занято”.
Пример
Лабиринт (n = 14, m = 12), карта которого представлена ниже, имеет площадь внутренних стен 104 ´ 3 = 312 м2 . Контуры внутренних стен на рисунке выделены жирной линией.

5. Азбука Морзе (4 балла)
Как хорошо известно, существует
телеграфный код (азбука Морзе), где каждый
из передаваемых символов кодируется
комбинацией точек и тире. Разные символы
кодируются различными по длине
последовательностями точек и тире. Символы
отделяются друг от друга временной паузой.
Например, сигнал SOS передается
последовательностью одиннадцати символов:
· три точки,
· пробел (пауза),
· три тире,
· пробел (пауза),
· три точки.
Предложите экономный способ
хранения длинного нераскодированного
сообщения в виде последовательности байтов.
Входные данные
Последовательность точек,
символов “тире” и пробелов.
Для сведения: под байтом
здесь понимается двоичное число, состоящее
из восьми двоичных разрядов-битов.
6. Разбиение на пары (2 + 7 = 9 баллов)
Пусть заданы два числовых
множества: {x1, x2, …, xn}
и {y1, y2, …, yn}.
Составим пары, сопоставив каждому xi некоторое
yj, перемножим числа каждой пары и
сложим получившиеся произведения.
Требуется найти такое разбиение чисел на
пары, при котором значение получившейся
суммы будет наименьшим.
Опишите эффективный (по времени)
алгоритм поиска требуемого разбиения.
Докажите, что найденный алгоритм
действительно правильно решает
поставленную задачу.
7. Принцы в лабиринте (9 баллов)
Имеется квадратный лабиринт,
состоящий из m рядов по m квадратных
комнат. Все комнаты имеют одинаковый размер.
В комнатах имеются двери (не более четырех),
ведущие либо в смежные комнаты, либо в
комнату-зал, где находится принцесса.
Все двери заперты на волшебные
замки. Тип каждого замка определяется
некоторым магическим словом. Среди замков
могут оказаться и одинаковые.
В каждой комнате имеется одна,
помеченная магическим словом, кнопка, при
нажатии на которую во всем лабиринте
одновременно открываются все замки, типы
которых совпали с магическим словом
нажатой кнопки. При отпускании кнопки все
замки закрываются.
В лабиринте находятся в
заточении b ³
1 персидских принцев. В каждую минуту
каждый из принцев может либо нажать, а затем
отпустить кнопку, либо перейти в соседнюю
комнату через открытую другим принцем
дверь.
Принцы, понимая, что, действуя
наудачу, они вряд ли доберутся до принцессы,
хотят заранее спланировать свои совместные
действия таким образом, чтобы хотя бы кто-то
из них добрался до зала (а потом принцесса
волшебным способом освободит всех
остальных).
Вы, как Верховный Визирь, знаете
план лабиринта, магические слова всех
замков и всех кнопок. Вам также известно,
где находится каждый из принцев.
Опишите алгоритм определения
минимального времени, необходимого для
освобождения принцев, если они,
руководствуясь вашими указаниями, будут
действовать наилучшим образом.
8. Графический формат (6 баллов)
Известно, что графические
изображения при использовании их на
компьютере представляются в специальных
графических форматах. Один из наиболее
простых графических форматов — формат PCX.
Опишем вкратце этот формат.
Пусть для простоты наше
изображение черно-белое. Каждую точку (пиксель)
нашего изображения будем кодировать одним
битом:
1 — белая точка,
0 — черная точка.
Тогда наше изображение будет
представляться последовательностью битов,
которую можно заменить
последовательностью байтов. Будем считать,
что число байтов всегда является целым.
Далее, если в нашей
последовательности идут подряд несколько
одинаковых байтов, то для экономии памяти
мы запишем этот повторяющийся байт с
коэффициентом повторения.
В формате PCX принято соглашение:
первые (старшие) два бита коэффициента (признак)
должны равняться двум единицам, далее
следуют шесть битов (счетчик), определяющие
коэффициент повторения.
Например, если некоторый байт
повторяется 9 раз, то перед ним следует байт-коэффициент
110010012 = = С916 = 20110 .
Если же байт не повторяется
несколько раз подряд, то он (байт)
записывается без такого коэффициента. Но из
последнего правила есть исключения. А
именно: если одиночный байт имеет такое
значение, что его можно ошибочно принять за
коэффициент, то перед ним записывается байт-коэффициент
со значением счетчика равным единице.
Опишите эффективный (по времени
работы) алгоритм определения количества
белых точек в заданном форматом PCX черно-белом
изображении.
Входные данные:
Последовательность байтов,
формирующих некоторое черно-белое
изображение.
Пример
Последовательность 201, 127, 193,
22, 66 интерпретируется следующим образом:
девять байтов со значением 127, один байт со
значением 22, один байт со значением 66.
9. Автомат (4 + 6 = 10 баллов)
В теории информации широко
известен код Хаффмена [17]. Код Хаффмена
строится отдельно для каждого текста.
Каждый символ, по Хаффмену, кодируется
последовательностью двоичных цифр, причем
более короткий код никогда не совпадает с
началом другого, более длинного, кода.
Например, может оказаться, что код буквы “е”
будет задан двоичным числом 1100, а код буквы
“х” — числом 1101110.
Закодированный таким способом
текст представляет собой
последовательность двоичных чисел,
выписанных подряд без пробелов (см. пример
закодированного фрагмента).
Некоторый текст был
проанализирован по алгоритму Хаффмена, и
были определены коды всех используемых в
данном тексте символов
|
|
Следующая таблица содержит всю
необходимую информацию и управляет работой
дешифрующего автомата.
Автомат считывает двоичные цифры
и меняет свое текущее состояние. Как
правило, нулевое состояние автомата
является начальным. В определенные моменты
автомат пишет в выходную строку очередной
раскодированный символ.
1. Догадайтесь, как работает этот автомат, и дешифруйте следующий фрагмент текста:
110011011100101010000011101101100101011
10101100101000011100100101111101011001
010010001011000000111101100101011100...
2. Опишите алгоритм работы дешифрующего автомата по управляющей таблице.
10. Операция над таблицами (1 + 2 + 1 = 4 балла)
Пусть имеются две табличные величины (двухмерные массивы) A и B. Над ними выполняется операция, которую мы будем обозначать символом “§”. Если C — результирующая табличная величина, то будем писать: C = A § B.
Пример. Ниже приведен результат C = A § B:
|
|
|||||||||||||||||||||||
| C | ||||
| 2•2+(–2)•0+(–3)•7 | 2•1+(–2)•(–2)+(–3)•3 |
= |
-17 | -3 |
| 1•2+4•0+0•7 | 1•1+4•(–2)+0•3 | 2 | -7 | |
| 3•2+0•0+2•7 | 3•1+0•(–2)+2•3 | 20 | 9 | |
| 1•2+5•0+1•7 | 1•1+5•(–2)+1•3 | 9 | -6 | |
1. Определите, как соотносятся
размеры таблиц A, B и С.
2. Сформулируйте алгоритм
вычисления элементов таблицы С = A §
B.
3. Вычислите C = A §
B при
|
|
|||||||||||||
11. (3 + 3 = 6 баллов)
Пусть дана таблица A. Клетки
таблицы могут иметь одно из трех значений:
0 — клетка пуста,
1 — в клетке находится яблоко,
2 — в клетке находится питон.
В начальный момент времени питон
занимает одну клетку таблицы. Далее питон
перемещается и растет по следующим
правилам:
· за один ход
голова питона перемещается в соседнюю (по
горизонтали или вертикали) клетку;
· если голова
питона переместилась в клетку с яблоком, то
питон съедает яблоко и его длина увеличивается
на единицу (при этом питон занимает все те
же клетки, которые он занимал до начала движения,
плюс та клетка, где находилось съеденное
яблоко);
· если голова
питона переместилась в пустую клетку, то
длина питона не изменяется, и все туловище
перемещается на одну клетку вслед за
головой;
· во всех
остальных случаях ход считается невозможным.
Пусть задана таблица A и
известен поклеточно предполагаемый
маршрут Z. Маршрут представляет собой
последовательность клеток, по которым
должна перемещаться голова питона. Каждая
клетка, начиная со второй, является
соседней по отношению к предыдущей клетке
маршрута. Первая клетка маршрута является
соседней к a1 . Будем считать, что в
каждый момент времени известна только одна
текущая клетка маршрута. Возвратиться к уже
использованным клеткам маршрута
невозможно.
Предостережение. Маршрут питона является предполагаемым, так как этот маршрут был проложен до того, как по клеткам таблицы разложили яблоки.
Пример
Пусть таблица имела вид, как
указано ниже, и предполагаемый маршрут Z
задан следующим образом: b1, c1, c2, c3.
Тогда в конце движения питон разместится в
таблице так, как показано на рисунке.
|
До начала движения |
По окончанию движения |
|||||||||
| a | b | c | d | a | b | c | d | |||
| 1 | 2 | 1 | 1 | 0 | 1 | 0 | 0 | 2 | 0 | |
| 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | |
| 3 | 1 | 0 | 0 | 1 | 3 | 1 | 0 | 2 | 1 | |
1. Докажите или опровергните следующее утверждение: невозможно проследить перемещение питона, если использовать только ограниченное количество переменных величин.
Примечание. Под ограниченным количеством переменных понимается такое их количество, которое не зависит от размера таблицы.
2. Сформулируйте алгоритм, который позволит определить расположение питона в процессе его движения по заранее заданному маршруту Z.
12. Ворона и сыр (10 баллов)
Ворона живет в Странном лесу. Весь
Странный лес разбит на квадраты со стороной 5 метров. В
каждом таком квадрате растет ель определенной
высоты. На макушке каждой ели лежит по кусочку сыра.
Ворона должна перелететь от ели с номером X к ели
с номером Y по кратчайшему маршруту.
Маршрут должен представлять собой
ломаную линию в пространстве, где каждый поворот
совпадает с макушкой некоторой ели (чтобы ворона могла подкрепиться кусочком сыра на повороте).
При прокладке маршрута считайте, что все ели (кроме
тех елей, где ворона делает остановку) представляют собой
препятствия в форме прямоугольных параллелепипедов (основание
— квадрат со стороной 5 метров, высота
параллелепипеда совпадает с высотой ели, макушка ели
совпадает с центром верхнего основания параллелепипеда).

Пролет вороны от одной ели напрямую (то
есть без поворотов) к другой ели считается
допустимым, если по пути ворона не пролетает сквозь
параллелепипед другой ели. Ели, где ворона делает поворот и
лакомится сыром, препятствиями не считаются!
Помогите нашей вороне проложить маршрут.
Для этого сформулируйте алгоритм поиска
кратчайшего маршрута, используя карту Странного леса с
обозначением высот всех деревьев.
13. Золотое дерево (8 баллов)
Пусть на поле дураков ровно в полночь посажено семечко золотого дерева. В первый день из семечка вырастает ствол единичной длины. За каждый последующий день каждая ветвь золотого дерева, включая ствол, вырастает в том же направлении еще на одну единицу длины. При этом каждый день в конце каждой ветви закладывается одна новая почка.
Пример роста золотого дерева (непроросшие почки обозначены кружками,
порядок ветвей — числами).
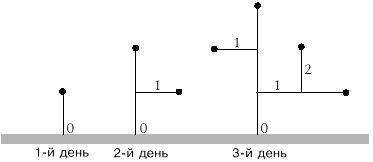
На следующий день из заложенных накануне
почек вырастают новые ветви единичной длины и т.д.
Ствол дерева считается ветвью нулевого
порядка. Порядок любой другой ветви на единицу
больше порядка ветви, откуда она произрастает.
По законам ботаники в полнолуние на
ветвях третьего порядка из еще не проросших почек
вместо побегов появляются золотые плоды.
Опишите алгоритм, позволяющий определить
количество золотых плодов, если полнолуние
произойдет через T дней.
14. Испорченная связь (4 балла)
Жители деревень Темяшкино и Мартышкино с давних времен пользуются для связи друг с другом специальным телеграфом. На окраинах этих деревень растут по четыре высоких дерева. На каждом дереве установлено сменное табло, на котором может быть показана одна из десяти цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Таким образом, одновременно может быть передано одно из 10000 четырехзначных чисел (от 0000 до 9999). Жители деревень заранее договорились и закодировали все возможные сообщения этими числами. Был издан справочник, в котором все сообщения были упорядочены по значимости: чем меньше номер сообщения, тем более оно значимо. В справочнике были указаны сообщения и их коды.

Но в канун 2000 года в деревне
Темяшкино с двух последних деревьев упали
цифры 9 (по-видимому, не были приняты меры к
решению “проблемы 2000 года”). Таким образом,
стало невозможно передавать числа, в записи
которых хотя бы одна из двух последних цифр
равна 9.
Жители решили не поднимать
упавшие цифры, потому что через каких-нибудь
сто лет планируется перейти на сотовые
телефоны, и отказались от менее значимых
сообщений. Если k — количество “потерянных”
кодов, то, следовательно, из справочника
были исключены последние k сообщений.
Специальная комиссия, созданная
для решения “проблемы 2000 года”, определила
процедуру пересчета принимаемого по
испорченному телеграфу кода в номер
сообщения по прежней классификации. Упорядоченность
сообщений по значимости по-прежнему
сохранилась.
Пример
Пусть по испорченному
телеграфу получен код 0020. Этот код
соответствует сsообщению № 18 из справочника,
так из предшествующих коду 0020 два кода — 0009
и 0019 — сейчас не используются.
Опишите алгоритм работы этой
процедуры.
15. Пропущенное число (5 баллов)
Ученик Ваня Петров записал n
чисел (n ³
3), образующих арифметическую
прогрессию. Затем Ваня одно число вычеркнул,
а оставшиеся числа перемешал.
Опишите алгоритм, который
проверяет, можно ли определить пропущенное
число, и восстанавливает его, если это
возможно.
16. Сортировка (3 + 4 = 7 баллов)
Пусть дана числовая последовательность X, состоящая из n элементов. Элементы, стоящие на четных позициях, упорядочены по возрастанию. То же самое касается и элементов, стоящих на нечетных позициях.
Пример
n = 10, X = (1, 10, 5, 11, 8, 12, 13, 22, 16, 254).
1. Сформулируйте рациональный
алгоритм вывода (печати) элементов
последовательности в порядке их
возрастания.
2. Переформулируйте предыдущий
алгоритм без использования дополнительной
памяти (то есть алгоритм работает только на
исходном массиве Х). Ответ обосновать.
17. Найди меня (6 баллов)
На моделях импортных кнопочных телефонных аппаратов цифровые кнопки промаркированы еще и латинскими буквами, кроме букв “Q” и “Z”, которые не используются.
Не вдаваясь в детали, отметим,
что это сделано для автоматизации
справочной службы [18]. Желающий воспользоваться
услугами автоматизированной справочной
службы выполняет следующие действия:
1) набирает номер
автоматизированной службы;
2) после ответа справочной службы
набирает фамилию абонента кнопками 2-9 (например,
фамилия “Knuth” набирается цифрами 5 6 8 8 4), затем
нажимает кнопку “*”;
3) набирает имя абонента (например,
имя “Donald” набирается цифрами 3 6 6 2 5 3), затем
нажимает кнопку “*”;
4) если абонентов оказывается
достаточно много, то компьютер запрашивает,
а пользователь соответственно вводит
дополнительную информацию (например, адрес);
5) выслушивает ответ справочной
службы.
Понятно, что при таком подходе
одна и та же цифровая последовательность
может соответствовать разным фамилиям.
Предложите и опишите вариант
организации базы данных клиентов,
включенных в автоматизированную
справочную службу. Опишите алгоритм поиска
клиента в базе данных. Ваш вариант
организации базы данных должен позволять
быстро находить сведения об абонентах по
цифровым аналогам их фамилий.
18. Алгоритм (2 балла)
1. Ввести исходные данные: A, B.
2. Если A = 0, то перейти на пункт
6.
3. Вычислить R = —B/A.
4. Напечатать R.
5. Стоп.
6. Если B = 0, то перейти на пункт
9.
7. Напечатать “нет”.
8. Стоп.
9. Напечатать “бесконечно много”.
10. Стоп.
Что делает данный алгоритм? Какая математическая задача решается этим алгоритмом?
ЗАДАЧИ ПРАКТИЧЕСКИХ ТУРОВ
1. Игра “Ним” (18 баллов)
Описание игры. Два участника поочередно называют натуральные числа, каждое из которых не превосходит некоторого значения N. Выигрывает тот участник, после хода которого сумма всех названных чисел достигнет или превысит заданное значение M.
Пример
Пусть N = 6, M = 30.
| Номер хода | Ход первого участника | Ход второго участника | Общая сумма |
| - | - | - | 0 |
| 1 | 6 | 6 | |
| 2 | 3 | 9 | |
| 3 | 6 | 15 | |
| 4 | 6 | 21 | |
| 5 | 2 | 23 | |
| 6 | 1 | 24 | |
| 7 | 6 | 30 |
Здесь седьмым ходом победил первый участник.
Задание
Составьте программу, которая играет с человеком в игру “Ним”. Программа должна стремиться, насколько это возможно, к выигрышу. Число сделанных ходов не учитывается.
Требования к программе
Программа будет тестироваться несколько раз. Первоначально программа запрашивает в диалоге номер теста (K). Входные данные K-го теста размещены в текстовом файле gameK.inp (здесь K — двузначный номер теста в диапазоне 01..50). Ход человека вводится с клавиатуры. Если ход человека некорректен, то программа выводит соответствующее сообщение и предлагает ввести ход повторно. Протокол игры выводится на экран дисплея и дублируется в выходной файл gameK.out в виде: номер хода, указание участника, ход участника и накопленная сумма после данного хода. Последняя строка протокола содержит указание, кто победил в данном тесте.
Формат входного файла
Во входном файле размещены 3 целых числа в следующем порядке: N, M, P. Здесь N — максимально возможный ход, M — предельная сумма, P — номер хода компьютера (1 — первым ходит компьютер, 2 — компьютер ходит вторым, т.е. первым ходит человек). Исходные числа размещены на одной или нескольких строках и разделяются одним или несколькими пробелами. Входные данные всегда корректны и удовлетворяют ограничениям: 1 £ N £ 1 000 000, 1 £ M £ 1 000 000, 1 £ P £ 2.
Пример входного файла game03.inp:
10 30 1
Пример выходного файла game03.out:
1 компьютер 10 10
2 человек
7 17
3 компьютер 10 27
4 человек
7 34
Победил человек
2. Игра “Супер-Ним” (33 балла)
Описание игры. Два
участника поочередно называют натуральные
числа. Причем называемое число может
отличаться от предыдущего числа (то есть
числа, названного соперником) не более чем
на 1. Выигрывает тот участник, после хода
которого сумма всех названных чисел
достигнет или превысит значение 20. Первый
ход первого игрока фиксирован и равен 1.
Пример
| Номер хода | Ход первого участника | Ход второго участника | Общая сумма |
| - | - | - | 0 |
| 1 | 1 | 1 | |
| 2 | 2 | 3 | |
| 3 | 2 | 5 | |
| 4 | 3 | 8 | |
| 5 | 2 | 10 | |
| 6 | 3 | 13 | |
| 7 | 4 | 17 | |
| 8 | 5 | 22 |
Здесь восьмым ходом победил второй участник.
Задание
Составьте программу, которая играет в игру “СуперНим”. Программа должна стремиться, насколько это возможно, к выигрышу. Число сделанных ходов не учитывается.
Требования к программе
Программа будет тестироваться несколько раз. Первоначально программа запрашивает в диалоге номер теста (K). Входные данные K-го теста размещены в текстовом файле sgameK.inp (здесь K — двузначный номер теста в диапазоне 01..50). Ход человека вводится с клавиатуры. Если ход человека некорректен, то программа выводит соответствующее сообщение и предлагает ввести ход повторно. Протокол игры выводится на экран дисплея и дублируется в выходной файл sgameK.out в виде: номер хода, указание участника, ход участника и накопленная сумма после данного хода. Последняя строка протокола содержит указание, кто победил в данном тесте.
Формат входного файла
Во входном файле размещено одно целое число P — номер хода компьютера (1 — первым ходит компьютер, 2 — первым ходит человек). Входные данные всегда корректны и удовлетворяют ограничению: 1 £ P £ 2.
Пример входного файла sgame03.inp:
1
Пример выходного файла sgame03.out:
1
компьютер 1 1
2 человек
1 2
3 компьютер
2 4
4 человек
3 7
5 компьютер
3 10
6 человек
4 14
7 компьютер
3 17
8 человек
3 20
Победил человек
3. Игра “Города” (25 баллов)
Описание игры. Вам наверняка известна игра “Города”. В ней игроки поочередно записывают названия городов таким образом, что каждое последующее слово начинается с последней буквы предыдущего слова: Рыбинск — Курск — Караганда — Амстердам... По условиям игры названия городов не могут повторяться. Двое игроков сыграли в эту игру, занося каждое слово в файл. После игры оказалось, что на компьютере был вирус City_Word, поэтому некоторые слова, возможно, были удалены, а оставшиеся оказались перемешанными.
Задание
Определить, можно ли из всех приведенных в заданном файле названий составить последовательность, отвечающую правилам игры. Если это невозможно, то вывести сообщение “нет решения” на экран дисплея. Если составить последовательность можно, то вывести сообщение “есть решение”; перечислить в алфавитном порядке все буквы, с которых может начинаться первое слово игры; перечислить в алфавитном порядке буквы, которыми может заканчиваться последнее слово игры.
Формат входного файла
В текстовом файле CITIES.TXT находятся неповторяющиеся слова — названия городов. Каждая строка файла содержит название только одного города. Названия записаны большими (заглавными) латинскими буквами. Никаких других символов, кроме заглавных латинских букв и признаков конца строк, в файле нет. Названия приведены в файле в произвольном порядке. Количество слов N удовлетворяет условию: 1 £ N £ 500. Название города состоит не менее чем из одной и не более чем из 255 букв.
Пример 1
Содержимое входного файла CITIES.TXT:
KARAGANDA
RYBINSK
KURSK
MURMANSK
Вывод на экран:
нет решения
Пример 2
Содержимое входного файла CITIES.TXT:
KARAGANDA
RYBINSK
KURSK
Вывод на экран:
есть решение
Первые буквы: R
Последние буквы: A
4. Операционная система (25 баллов)
Ученик Вова Воротов решил
создать новую операционную систему.
Реализацию своего проекта он начал с
написания модуля поддержки файловой
системы. Для экономии места на диске имя
каждого файла его операционной системы
состоит из одной латинской буквы (без учета
регистра).
В операционную систему Вовы
встроено много полезных возможностей.
Среди них — вывод списка файлов, в котором
файлы упорядочены по размеру.
Для выполнения этой операции
используется алгоритм, точное содержание
которого известно и понятно только Вове.
Известно лишь, что файлы сравниваются по
размерам и результат сравнения
записывается в файл протокола.
Ядро файловой системы, в том
числе и процедура определения размера
файла, все еще содержит ошибки.
При просмотре файла протокола
Вова обнаружил там сообщение о том, что,
возможно, при определении размера одного
файла произошла ошибка. Кстати, система
контроля над ошибками тоже пока не отлажена.
Задание
Помогите Вове проанализировать
файл протокола OS.IN и проверить, имеется ли в
нем логическое противоречие. Если
противоречие будет обнаружено, значит, была
допущена одиночная ошибка при определении
размера одного из файлов.
Если ошибка произошла, то
выведите в алфавитном порядке список имен
файлов, при определении размеров которых
могла произойти ошибка. Если же ошибки не
было (т.е. нет логического противоречия), то
определите, какие из файлов могут иметь
наибольший размер, и выведите их имена в
алфавитном порядке. Результат анализа
поместите в выходной файл OS.OUT. Кроме того,
вы можете помочь Вове придумать название
для его новой операционной системы. (Помощь
в этом нелегком деле поощряется. За лучшее
название назначена награда — 0,5 балла.)
Формат входного файла
В текстовом файле OS.IN находятся следующие данные. Первая строка файла содержит количество сравнений (К). Последующие К строк содержат имена файлов, разделенные знаком “<” или “>”. Количество сравнений К удовлетворяет условию: К ³ 1. Каждый из имеющихся файлов упомянут в протоколе хотя бы один раз.
Формат выходного файла
В выходном текстовом файле OS.OUT должно содержаться сообщение “противоречие не обнаружено” или “обнаружено противоречие”. В первом случае указываются количество возможных файлов наибольшего размера и их имена в алфавитном порядке. Во втором случае указываются количество возможных неверных сравнений и в алфавитном порядке имена файлов, при определении которых могла быть допущена ошибка.
Пример 1
Содержимое входного файла
OS.IN:
3
a > B
B > C
b < C
Содержимое выходного файла OS.OUT:
обнаружено противоречие
2
B
C
Пример 2
Содержимое входного файла OS.IN:
3
A > B
B > C
d > C
Содержимое выходного файла OS.OUT:
противоречие не обнаружено
2
A
D
5. Упрощение выражения (26 баллов)
Задание
Задана строка, состоящая из
однолитерных идентификаторов-переменных,
знаков умножения, деления и круглых скобок.
Проверьте, является ли данная строка
корректной записью арифметического
выражения, и если выражение корректно, то
упростите его.
Правила упрощения. Выражение
будет считаться упрощенным, если в его
итоговой записи:
· каждый
идентификатор (переменная) встречается не
более одного раза;
·
идентификатор всегда имеет положительную
степень, степень записывается
положительным целым числом, большим 1 (степень,
равная 1, не записывается);
·
знаменатель, не содержащий идентификаторов,
не записывается;
· если
выражение является дробью, то числитель и
знаменатель отделяются друг от друга одним
знаком “/”;
· числитель,
не содержащий идентификаторов, записывается
в виде единицы;
· при
необходимости знаменатель может быть заключен
в скобки (но не более одной пары), числитель
в скобки никогда не заключается.
Формат входных данных
Текстовый файл входных данных INPUT.TXT содержит несколько строк. В первой строке задано целое число n (1 £ n £ 1000), соответствующее количеству последующих строк. Каждая из следующих строк файла задает некоторое выражение. В записи выражения могут использоваться идентификаторы переменных — заглавные латинские буквы, круглые скобки и знаки деления и умножения: “/”, “*”. Выражения во входном файле не содержат в своей записи никаких иных символов, но могут быть записаны некорректно. Результирующая степень любого идентификатора не превышает 128.
Формат выходных данных
В выходной текстовый файл OUTPUT.TXT должны быть выведены n строк, каждая из которых соответствует либо итоговой записи выражения после упрощения (согласно описанным в условии правилам), либо строке “ERROR”, если строка не является корректным выражением.
Предупреждение. В итоговую запись, кроме символов входной строки, дополнительно могут входить символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (для задания числителя и для задания показателей степеней) и “^” (знак операции возведения в степень).
Пример входного файла INPUT.TXT:
5
A/(B*E*A/(A*A*C*A*Z))*Z
A*A)
ABC
A/(A*A)/A/A
A/(A)
Пример выходного файла OUTPUT.TXT:
A^3*C*Z^2/(B*E)
ERROR
ERROR
1/A^3
1
6. Ломаная линия (16 баллов)
На клетчатой бумаге нарисован
квадрат размером n на n клеток. Некто
проводит из левого нижнего угла квадрата
ломаную линию. Каждое звено ломаной параллельно
какой-либо стороне квадрата. Звенья с нечетными
номерами горизонтальны, с четными — вертикальны.
Вершины ломаной линии совпадают с углами
клеток, а вся ломаная линия не должна
выходить за пределы квадрата.
Проведенная ломаная линия
задается последовательностью целых чисел.
Каждое число характеризует одно звено
ломаной и по модулю равно длине звена. При
этом для горизонтальных звеньев
направление вправо при рисовании ломаной
задается положительными числами, а
направление влево — отрицательными
числами; для вертикальных звеньев
положительное направление — это
направление вверх, а отрицательное — вниз.
Пример
Пусть n = 12.
Последовательность чисел: 3, 6, —2, 4, 4, —7 (три
клетки вправо, шесть клеток вверх, две
клетки влево, четыре клетки вверх, четыре
клетки вправо, семь клеток вниз)
соответствует ломаной, изображенной на
рисунке (X — начало ломаной, Y —
конец ломаной).
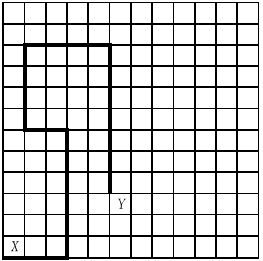
Определение. Будем говорить, что ломаная имеет самопересечения, если найдется хотя бы одна точка, принадлежащая одновременно двум различным звеньям, либо найдутся две совпадающие вершины.
Пример
Следующие ломаные имеют
самопересечения (проверьте!):
· 3, 6, —2, 4, 4,
—7, —2;
· 3, 6, —2, 4, 4,
—4, —2;
· 3, 6, —2, 4, 4,
—7, —3.
Задание
Пусть заданы n — размер квадрата, m — количество звеньев и L1 , L2 , …, Ln — числовая последовательность, описывающая ломаную. Проверить, не выходит ли ломаная за пределы квадрата и имеет ли ломаная самопересечения.
Формат входных данных
Текстовый файл входных данных INPUT.TXT содержит в первой строке два целых числа: n — сторона квадрата (1 £ n £ 20), m — количество звеньев ломаной линии (1 £ m £ 500). Далее следуют m целых ненулевых чисел. Числа разделяются одним или несколькими пробелами и/или признаком конца строки. Эти числа задают длины и направления отдельных звеньев. Файл исходных данных находится в текущем каталоге.
Формат выходных данных
В выходной текстовый файл OUTPUT.TXT
вывести сообщение:
· “ошибка”,
если ломаная выходит за пределы квадрата;
· “да”, если
ломаная не выходит за пределы квадрата и
имеет самопересечения;
· “нет”,
если ломаная не выходит за пределы квадрата
и не имеет самопересечений.
7. Восстановление ошибок (26 баллов)(Описываемый в задаче принцип принадлежит Р.Р. Варшамову и Г.М. Тененгольцу.)
Общие сведения. Пусть
имеется канал связи, по которому передаются
кодированные сообщения. Каждое сообщение T
= S1, S2, …,Sm
разбито на m двоичных слов
фиксированной длины: Sk = x1x2
… xn, где xi = {0, 1} —
двоичный символ. Передаваемые слова
назовем кодовыми словами или просто
словами. Пусть принятое сообщение имеет вид:
T ' = S '1, S '2, …, S 'm
.
Будем считать, что вследствие
ненадежной работы аппаратуры при передаче
каждого из m кодовых слов возможны
следующие ошибки:
1) потеря одного (любого) символа;
2) замена одного нулевого символа
единичным (замена единичного символа
нулевым считается невозможной!);
3) передача одного (любого)
дополнительного символа (в произвольном
месте).
Предполагается, что при передаче
одного кодового слова может иметь место
ошибка только одного типа из данного
перечня.
Очевидно, что в общем случае
невозможно установить, имела ли место
ошибка, и тем более невозможно эту ошибку
исправить.
Дополнительное условие.
Предположим, по каналу связи передаются
только кодовые слова, удовлетворяющие
условию: (1•x1 + 2•x2 + … + n•xn
) mod p = 0, где p = n + 1 (A mod B
— операция взятия остатка при
целочисленном делении A на B).
Пример 1
Пусть n = 4. Тогда p = 4 + 1 = 5. Пусть принято кодовое слово S ' = 10101. Уже по длине кодового слова видно, что имела место ошибка третьего типа.
Пример 2
Пусть n = 4, p = 4 + 1 = 5, S ' = 1101. Так как длина принятого кодового слова совпадает с требуемой, но нарушено дополнительное условие, то очевидно, что имела место ошибка второго типа. Если заменить второй (слева) символ на нулевой, то будем иметь S = 1001, и дополнительное условие в этом случае выполняется.
Задание
Пусть в исходном текстовом
файле содержатся значения n, m и
некоторые двоичные кодовые слова. Длина
каждого слова отличается от n не более
чем на 1. Проверьте, возможно ли
восстановить переданные кодовые слова,
исправив не более одной ошибки.
По каждому кодовому слову
необходимо:
· вывести
принятое слово, если ошибки нет (то есть
выполняется дополнительное условие);
· вывести
исправленное значение кодового слова, если
при передаче имела место ошибка и ее
возможно исправить (однозначно);
· вывести
сообщение о неисправимой ошибке “ERROR”,
если невозможно выполнить один из
предшествующих пунктов.
Формат входных данных
Текстовый файл входных данных INPUT.TXT содержит в первой строке два числа: n — количество двоичных символов в передаваемых словах, m — количество переданных слов (1 < n £ 255, 0 £ m £ 1000). Последующие m строк содержат m двоичных слов (записанных как обычные строки) по одному слову на строке. Числа n и m разделяются пробелами. В последующих строках записаны только нули и единицы (без пробелов). Длина всех строк исходного файла не превосходит 255. Текстовый файл исходных данных находится в текущем каталоге.
Формат выходных данных
В выходной текстовый файл OUTPUT.TXT вывести m строк, содержащих исправленные слова. Если некоторое слово, по вашему мнению, невозможно исправить, то вывести вместо него в выходной файл строку “ERROR” (заглавными латинскими буквами).
Пример входного файла INPUT.TXT:
4 5
1001
10101
0110
0101
110
Пример выходного файла OUTPUT.TXT:
1001
1001
0110
ERROR
0110
Решения задач
ТЕОРЕТИЧЕСКИХ ТУРОВ
1. Алгоритм (2 + 3 = 5 баллов)
Решение
Описанный алгоритм (идею задачи автор почерпнул из книги Дональда Бентли “Жемчужины творчества программистов” [18]) выполняет циклический сдвиг элементов массива вправо следующим образом. Массив делится на 2 части: первая часть — от 1-го элемента до k-го, вторая часть — от (k + 1)-го элемента до n-го. Циклический сдвиг вправо выполняется отдельно для каждой части (независимо от другой) так, что последний элемент части становится первым в этой же части массива.
Пример
Пусть k = 4 и X = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
| Выполняемое действие | Массив X |
| Reverse(1, n) | (9, 8, 7, 6, 5, 4, 3, 2, 1, 0) |
| Reverse(k + 1, n) | (9, 8, 7, 6, 0, 1, 2, 3, 4, 5) |
| Reverse(1, k) | (6, 7, 8, 9, 0, 1, 2, 3, 4, 5) |
Докажем это утверждение.
Пусть исходный массив имеет вид:
X = (X1,
…, Xn—k—1, Xn—k, Xn—k+1,
…, Xn ).
После первого вызова Reverse(1, n)
массив “перевернется” и примет вид:
X ' = (Xn,
…, Xn—k+1, Xn—k, Xn—k—1,
…, X1 ).
Второй вызов Reverse(k + 1, n)
“перевернет” только часть массива,
начиная с (k + 1)-го элемента и заканчивая
последним:
X '' = (Xn,
…, Xn—k+1, X1, …, Xn—k—1,
Xn—k ).
И, наконец, последний вызов Reverse(1,
k) поставит точку в наших
преобразованиях:
X ''' = (Xn—k+1,
…, Xn, X1, …, Xn—k—1,
Xn—k ).
Таким образом, утверждение доказано.
2. Таблица (2 балла)
Решение
Правильное решение основано на последовательном обходе доски, гарантирующем раньше или позже достижение ненулевой клетки. Возможны различные маршруты таких обходов. В качестве примера рассмотрим обход “по диагоналям”: (1; 1), (2; 1), (1; 2), (3; 1), (2; 2), (1; 3), … Ниже приведен фрагмент соответствующей программы на Паскале.
i:=1;
j:=1;
while "клетка (i, j) – нулевая" do
if i=1 then
begin {переход на
следующую диагональ}
i:=j+1; j:=1
end
else {движение по текущей диагонали}
begin
i:= i-1;
j:=j+1
end
3. Последовательность (2 + 5 = 7 баллов)
Решение
Рассмотрим отдельные случаи.
Отметим различие между n и k. Если
параметр k должен быть зафиксирован, то n
может быть любым!
1. Пусть k = 2p. В качестве n
выберем любое нечетное число, большее
единицы. Тогда при каждом выполнении пункта
3 значение n увеличивается на k и
остается при этом нечетным. Следовательно,
в этом случае в выстраиваемой
последовательности будут только нечетные
возрастающие числа. Но тогда описанные
действия будут строить бесконечную
последовательность, а следовательно, они не
могут рассматриваться в качестве алгоритма,
так как алгоритм обязан обладать свойством
конечности, то есть остановиться через
конечное число шагов.
2. Пусть k = 2p + 1 (при p >
0). Рассмотрим, как изменяется значение n.
Для этого выберем начальное значение n0
= k.
Далее будем иметь:
n1 = n0
+ k = k + k = 2k,
n2 = n1/2
= 2k/2 = k
— и т.д.
Следовательно, и в этом случае
анализируемая последовательность действий
не обладает свойством конечности.
3. Пусть k = 1. Покажем, что в
этом случае свойство конечности имеет
место. Для этого докажем, что
подпоследовательность np, np+2, np+4
, … является убывающей, начиная с
некоторого p. Выберем в качестве
стартового np некоторое нечетное
значение a, большее единицы. (Если взять a
= 1, то вычисление будет сразу прекращено по
пункту 2.) Действительно, имеем:
np = a,
np+1
= np + k = a + 1,
np+2
= np+1 /2 = (a + 1)/2.
Вычислим разность np+2 — np:
np+2 — np = (a + 1)/2 — a = (a + 1 — 2a)/2 = (1—a)/2 < 0
Таким образом, названная
подпоследовательность является убывающей
последовательностью натуральных чисел.
Следовательно, последовательность конечна.
Теперь можно сформулировать
окончательный ответ: сформулированный в
условии алгоритм обладает свойством
конечности только при k = 1.
4. Оклеивание лабиринта (3 балла)
Решение
Правильный алгоритм состоит из
вычисления внутреннего периметра всех стен
и умножения этого периметра на высоту
лабиринта. Так как решение достаточно
просто, то рассмотрим только основную идею
алгоритма.
Для нахождения периметра
достаточно последовательно перебрать все
клетки лабиринта и просуммировать
количество примыкающих к каждой пустой
клетке участков стен.
Пример
В пустых клетках лабиринта указано количество примыкающих к ним оклеиваемых участков стен. Общее количество этих участков равно 104. Для нахождения площади необходимо умножить периметр на высоту: 104 ´ 3 = 312 (м2 ).

5
. Азбука Морзе (4 балла)Решение
Как всегда, возможны самые
различные варианты решения задачи. Автору
более всего импонирует способ, основанный
на использовании длинного троичного числа.
Например, отождествим пробел с цифрой 0,
знак тире — с цифрой 1, знак точки — с цифрой
2. Тогда закодированное сообщение — это
длинное число в троичной системе счисления.
Такое число можно упаковать в
последовательность байтов. Для этого
удобнее всего преобразовать троичное число
в двоичное число. Дополнительно придется
зафиксировать длину сообщения.
Второй вариант кодирования
заключается в следующем. Выделим для
кодирования каждого символа переданного
сообщения два бита:
— “·” (точка)
— 00,
— “_” (пробел) — 01,
— “—” (тире) – 10,
— признак конца сообщения — 11.
6. Разбиение на пары (3 + 5 = 8 баллов)
Решение
Можно было бы сгенерировать все
возможные сочетания пар элементов массивов
и выбрать наилучший вариант (n! ´
n! вариантов). Понятно, что можно поступить
проще: зафиксировать порядок следования
элементов одного массива и порождать все
возможные перестановки элементов второго
массива (n! вариантов). Но также понятно,
что такое решение не имеет смысла даже при
небольших размерах массивов!
Правильное решение основано на
предварительной сортировке исходных
массивов. Упорядочим массив X по
возрастанию, а массив Y оставим в
исходном состоянии.
Рассмотрим сумму
S = x1 • y1 + x2 • y2 + … + xn • yn.
Выберем произвольную пару yi, yj, такую, что i < j и yi < yj . (Если такой пары нет, значит, массив Y упорядочен по убыванию.) Рассмотрим разность:
(xi • yi
+ xj • yj ) — (xi • yj
+ xj • yi ) =
= xi • yi
+ xj • yj — xi • yj
— xj • yi =
= xi • (yi
— yj ) + xj • (yj — yi
) =
= (xi — xj
) • (yi — yj ) > 0.
То есть сумма S может быть уменьшена
всякий раз, пока массив Y остается
неупорядоченным по убыванию.
Таким образом, сумма S будет
минимальна тогда и только тогда, когда
массив X упорядочен по возрастанию, а
массив Y упорядочен по убыванию.
7. Принцы в лабиринте (9 баллов)
Решение
Разобьем решение задачи на
этапы: построение некоторой формальной
модели и определение минимального времени.
Будем считать, что все клетки лабиринта
пронумерованы.
Формальная модель задачи — это
специального вида граф. Вершины графа — это
последовательности номеров комнат, где
находятся принцы. Дуги графа будут означать
допустимые перемещения принцев за одну
единицу времени.
Пример
Вершина (1, 5, 5, 2) означает, что
первый принц находится в комнате 1, второй и
третий принцы находятся в комнате 5,
четвертый принц находится в комнате 2.
Про вершину графа будем говорить,
что она соответствует некоторому
размещению принцев в лабиринте. Построим
множество всех возможных размещений. Это
множество будет конечно.
Каждый из принцев может в каждый
момент времени попытаться выполнить одно
из действий:
· встать на
кнопку,
· шагнуть на
“север”,
· шагнуть на
“юг”,
· шагнуть на
“восток”,
· шагнуть на
“запад”.
Вариант, когда принц ничего не
предпринимает, можно отождествить с
вариантом, когда принц встает на кнопку.
Понятно, что некоторые действия могут быть
невозможны в конкретной ситуации.
Свяжем направленными дугами те
вершины-размещения в построенном графе, для
которых возможен переход из одного
размещения в другое размещение за один шаг,
то есть когда каждый из принцев выполняет
одно определенное действие из
вышеупомянутого списка.
Проверка перехода из одного
размещения в другое достаточно проста,
поэтому на ней мы не будем останавливаться.
После того как в графе будут
проведены все дуги, выделим вершину,
соответствующую начальному размещению, и
вершины, соответствующие конечным размещениям.
Конечных или заключительных вершин может
оказаться несколько, так как принцессу
могут освободить разные принцы. Если
заключительных вершин не окажется, то
принцы не смогут освободить принцессу.
Теперь предстоит определить
минимальное время. Для этого необходимо
построить минимальной длины путь, ведущий
из начальной вершины в любую заключительную.
Последнее легко выполняется
волновым алгоритмом, описанным ниже.
1. Положить i равным нулю (i
= 0).
2. Пометить начальную вершину
числом i.
3. Если любая из заключительных
вершин помечена числом i, то перейти на
пункт 8.
4. Составить список Т из всех
вершин с пометкой i.
5. Для всех вершин X из
сформированного списка Т выполнить
действие 5.1.
5.1. Пометить числом (i
+ 1) все вершины, которые не были ранее
помечены и одновременно являются
достижимыми из вершины X за один шаг.
6. Увеличить i на
1 (i = i +
1).
7. Перейти на пункт 3.
8. Вывести величину i (минимальное
время).
8. Графический формат (6 баллов)
Решение
Основная сложность задачи заключается в
понимании довольно длинного текста условия,
хотя решение не является сложным. Возможны различные
варианты.
1. Выделяем повторяющиеся байты, после
чего в каждом из них (через сдвиг или деление на 2)
выделяем единичные биты. Это плохое решение.
2. Выгоднее сначала подсчитать, сколько
раз встречается каждый байт, а только потом или через
заранее подготовленный массив констант, или
другим способом подсчитать количество единичных
битов.
Второй момент, на который следует
обратить внимание, — это правильная идентификация
очередного байта. Выгоднее всего сравнивать числовое
значение байта с заранее подсчитанной маской (110000002192). Если
байт есть коэффициент, то вычитанием из
него значения 192 получаем непосредственно
повторитель.
Итак, в решении должны присутствовать
моменты:
· инициализация
массива счетчиков байтов;
· цикл чтения
байтов;
· анализ
текущего байта (сравнение с числом 192);
· вычисление
повторителя (вычесть 192);
· увеличение
счетчика выделенного байта на значение повторителя или на 1 (единичный
байт);
· подсчет числа
единичных битов для каждого из 256 возможных байтов.
9. Автомат (5 + 5 = 10 баллов)
Решение
Эта задача больше всего понравилась
участникам. В тексте условия прямо говорится о кодах
символов “е” и “х”. Эти же символы есть и в управляющей
таблице автомата. Следовательно, надо найти
принцип размещения этих и других символов в таблице.
“Входом” в таблицу служат номер столбца
и номер строки [17]. Столбцы пронумерованы числами 0
и 1. Можно предположить, что это значения
битов из декодируемой строки. Тогда легко догадаться,
что строки — это состояния автомата (о них говорится в
условии задачи, и начальное состояние называется
нулевым).
Таким образом, по-видимому, основной цикл
работы автомата следующий:
1) установить автомат в начальное (нулевое)
состояние S;
2) если входная строка закончена, то
прекратить работу, иначе перейти к следующему пункту;
3) прочитать бит B из входной строки;
4) прочитать клетку таблицы с координатами
(S, B);
5) если в клетке записана буква C,
то вывести ее в выходную строку, перейти в состояние
S = 0 и перейти на пункт 2;
6) если в клетке записано число N,
то установить состояние S = N и
перейти на пункт 2.
Проверим описанный алгоритм на нашем примере.
Первоначально имеем B = 1 и S
= 0. По таблице
определяем новое состояние S =
10, а из входной строки считываем новый бит B
= 1. Находим
следующее состояние S =
21. В следующей таблице показано, как меняется состояние автомата (C
—
декодированный символ).
| B | S | C |
| 1 | 0 | |
| 1 | 10 | |
| 0 | 21 | |
| 0 | 22 | e |
| 1 | 0 | |
| 1 | 10 | |
| 0 | 21 | |
| 1 | 22 | |
| 1 | 23 | |
| 1 | 24 | |
| 0 | 25 | x |
| 0 | 0 | |
| 1 | 1 | |
| 0 | 4 | a |
| 1 | 0 | |
| 0 | 10 | |
| 1 | 11 | |
| 0 | 14 | |
| 0 | 15 | l |
Окончательный ответ — это начало фразы из стихотворения Маршака: “Ехали медведи на велосипеде…”.
10. Операция над таблицами (1 + 2 + 1 = 4 балла)
Решение
В задаче используется операция умножения
двух матриц. Безусловно, старшеклассники могут
знать об этой операции, но жюри рассчитывало, что для
лидеров эта задача не будет представлять интереса,
поэтому эта задача была, что называется, “без подсказки”.
Далее табличные величины будем называть матрицами.
1. Количество столбцов первой матрицы
должно совпадать с количеством строк второй матрицы.
Это хорошо видно из примера в условии задачи,
так как результирующие выражения состоят из
суммы попарных произведений. Следовательно,
должно совпадать количество таких сомножителей.
Размер матрицы C определяется
размерами таблиц A и B:
количество строк C совпадает с
количеством строк A,
количество столбцов C совпадает с количеством столбцов
B.
2. Алгоритм вычисления произведения двух
матриц Cm´k
= Am´n
• Bn´k
основан на применении формулы:
![]()
Алгоритм вычисления C представляет
собой тройной цикл по переменным i, j,
p.
Во внутреннем цикле выполняется накопление суммы
Ci, j .
3. Ответ представлен ниже.
| C | ||
| 2•(–2) + (–2)•3 + (–3)•5 | = |
–25 |
| 1•(–2) + 4•3 + 0•5 |
10 |
|
11. Питон (3 + 3 = 6 баллов)
Решение
1. Опровергнуть это утверждение
можно, предъявив соответствующий алгоритм.
Предположим, что такой алгоритм существует.
Рассмотрим питона, который
полностью занимает некоторую
прямоугольную область таблицы. Конечно,
можно зафиксировать, где находится голова и
где находится хвост питона. Но этого
недостаточно. Пусть далее необходимо
передвинуть питона. Возникает вопрос: какой
участок туловища из двух соседних с головой
клеток должен переместиться вслед за
головой? Это невозможно определить, если не
зафиксировать связь каждого элемента
туловища питона с предыдущим!
Если же выделить память для
хранения “ссылок” (можно назвать эти
ссылки скелетом или хребтом питона), то эта
память по размеру сопоставима с размером
питона, который, в свою очередь, может
занять всю исходную таблицу.
2. Ответом на второй вопрос
является конкретный алгоритм, использующий
дополнительную память. Можно, например,
создать динамический список.
Можно поступить по-другому:
используем вторую таблицу, равную по
размерам с исходной таблицей. В этой
таблице будем фиксировать местоположение
головы питона и в каждой клетке-туловище
будем записывать одно из четырех значений,
определяющих местоположение предыдущей
клетки-туловища. Размещение яблок во второй
таблице не фиксируется.
| a | b | c | d | |
| 1 | 0 | 0 | 4 | 0 |
| 2 | 0 | 0 | 4 | 5 |
| 3 | 0 | 0 | 1 | 2 |
На рисунке размещен пятиклеточный питон, голова которого находится в клетке d2, за ней размещено туловище: d3 ® c3 ® c2 ® c1. Здесь значение 1 задает ссылку вправо, значение 2 — ссылка вверх, значение 3 — ссылка влево, значение 4 — ссылка вниз, значение 5 — голова питона, значение 0 — пустая клетка.
12. Ворона и сыр (10 баллов)
Решение
Решение данной задачи состоит
из двух основных моментов. Первый —
построение формальной модели, где будут
отражены все возможные маршруты. Второй —
нахождение его кратчайшего маршрута.
Первая часть предполагает
использование геометрии. Соединим каждую
пару елей между собой отрезком прямой.
Далее проверим, какие из этих отрезков допустимы,
то есть не задевают других елей. Для этого
нужно уметь проверять взаиморасположения
отрезка прямой и параллелепипеда. Оставим
только те отрезки, которые допустимы для
пролета вороны.
Получаем взвешенный граф, в
котором вершины — это макушки елей, а ребра
— это допустимые маршруты. Далее нужно
найти кратчайший путь в графе. А это уже
классическая задача, которая решается
многими алгоритмами. Например, можно
применить алгоритм Дейкстры (весьма схожий
с вариацией волнового алгоритма).
13. Золотое дерево (8 баллов)
Решение
Составим следующую таблицу, в которой отмечено количество почек на ветвях разных порядков
| День | Kоличество почек на ветвях указанного порядка | ||||||
| k \ i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 2 | 1 | 0 | 0 | 0 | 0 |
| 4 | 1 | 4 | 2 | 1 | 0 | 0 | 0 |
| 5 | 1 | 8 | 4 | 2 | 1 | 0 | 0 |
| 6 | 1 | 16 | 8 | 4 | 2 | 1 | 0 |
| 7 | 1 | 32 | 16 | 8 | 3 | 2 | 1 |
Пусть Pk, i — количество почек в k-й день на ветвях i-го порядка.
| Pk, i = | 1, i = 0 | |
| 2k-i-1, k > i > 0 | ||
| 0, k £ i |
14. Испорченная связь (4 балла)
Решение
Совершенно неожиданно для
автора эта задача оказалась не по силам
участникам и была отмечена как самая
неудачная. Возможные причины такого
отношения к задаче сформулированы ниже.
1. Недостаточно четкая
формулировка задачи.
2. Малое количество баллов.
3. Плохое знание систем счисления.
Ниже приведена другая, более
формализованная, формулировка этой задачи.
Рассмотрим последовательность
четырехзначных чисел от 0000 до 9999. Занесем
эти числа в таблицу, в которой первый
столбец — порядковый номер числа,
записанного во втором столбце.
| Номер | Четырехзначное число |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0002 |
| ... | ... |
| 8 | 0008 |
| 9 | 0009 |
| 10 | 0010 |
| ... | ... |
| 9999 | 9999 |
Удалим из таблицы строки,
соответствующие числам, в записи которых в
последних двух позициях встречается цифра 9
(хотя бы в одной из двух). А теперь заново
перенумеруем эти числа. Например, число 0010
будет сейчас иметь номер 9. Общее количество
оставшихся чисел вычисляется по формуле: 10
• 10 • 9 • 9 = 8100. Учитывая, что нумерация в
таблице начинается с нуля, последнее число
9988 будет иметь номер 8099.
Требуется определить процедуру
вычисления порядкового номера в полученной
таблице.
Возможны несколько решений нашей
задачи. Первое из них основано на
буквальном пересчете наших чисел. Для этого
можно последовательно порождать числа,
проверять их на наличие цифры 9 в последних
двух позициях и одновременно считать
порожденные (без девяток) числа. Условие
окончания цикла — порождение искомого
числа.
Но на самом деле авторская идея
заключалась совсем в другом.
Обратим внимание, что в записи
двух последних разрядов используются
девять цифр — от 0 до 8. Поэтому можно
считать, что здесь применяется
девятеричная система счисления. В то время
как первые две цифры представляют собой
запись числа в десятичной системе счисления.
Далее можно определить вес
каждого разряда. Четвертый и третий разряды
“переполняются” после цифры 8, поэтому их
вес равен 9. Вес второго разряда равен 10, а
вес первого разряда, также равный 10, нам не
пригодится.
Можно сказать, что наши числа
записываются в смешанной системе счисления
(В литературе по системам
счисления [19] термин “смешанная система
счисления” применяется для обозначения
так называемых P—Q-ичных систем. Примером
такой системы может служить двоично-десятичная
система, в которой каждая десятичная цифра
записана в виде четырехзначного двоичного
числа. Можно было бы предложить для таких
целей более удачный термин “вложенные
системы счисления”, оставив “смешанные”
для случая, когда в записи отдельных
разрядов применяются различные системы
счисления.).
Пусть искомое число записывается
в виде abcd, где a, b, c и d —
соответствующие цифры. Тогда порядковый
номер числа (или его десятичное
представление) вычисляется по формуле:
a • 10 • 9 • 9 + b • 9 • 9 + c • 9 + d.
Примеры
1) 0010 = 1 • 9 = 9,
2) 0088 = 8 • 9 + 8 = 80,
3) 0100 = 1 • 9 • 9 = 81,
4) 2871 = 2 • 10 • 9 • 9 + 8 • 9 • 9 + 7 • 9 + 1
= (((2 • 10 + 8) • 9 + 7) • 9 + 1) = 2332,
5) 3000 = 3 • 10 • 9 • 9 = 2430,
6) 9988 = 10000 — 1 = 1 • 10 • 10 • 9 • 9 — 1 =
8100 — 1 = 8099.
15. Пропущенное число (5 баллов)
Решение
Прежде всего перечислим
ситуации, когда невозможно установить
пропущенное число:
· вычеркнуто
первое число;
· вычеркнуто
последнее число;
· при n = 3
вычеркнуто любое число.
Далее можно упорядочить заданные
числа, и если разность между любыми двумя
соседними числами будет одинакова, то
восстановить число невозможно.
Если же найдутся два соседних
числа X и Y с удвоенной разностью (по
сравнению с другими разностями), то
пропущено число z = (X + Y)/2.
Второй вариант решения основан
на анализе числовых характеристик заданной
последовательности.
При чтении входной
последовательности вычислим сумму S и
определим числа max, max1, max2,
min.
Здесь
max — максимальное число,
max1 и max2 —
ближайшие к нему числа последовательности,
min — минимальное число.
Затем вычислим разности
d1 = max — max1
и d2 = max1 — max2.
Отсюда можно определить шаг
последовательности:
h = (max — min)/(n
— 1).
Например, для последовательности
(3, 5, 8, 2, 9, 4, 6) имеем n = 8 (одно число
вычеркнуто), S = 29, max = 9, max1 =
8, max2 = 6, min = 2, d1 = 1, d2
= 2, h = 1.
Рассмотрим четыре случая.
1. Пусть d1 > d2.
Пропущенное число вычисляется по
формуле:
z = (max
+ max1 )/2.
2. Пусть d1 < d2.
Пропущенное число вычисляется по
формуле:
z = (max1
+ max2 )/2.
3. Пусть h = d1 = d2.
Пропущенное число вычисляется по
формуле:
z = (max
+ min)•n/2 — S.
4. Пусть b ¹
d1 = d2.
В таком случае определить
отсутствующее число невозможно.
Пример
Для приведенной выше последовательности имеем d1 < d2 . Отсюда находим пропущенное число z = (8 + 6)/2 = 7.
16. Сортировка (3 + 4 = 7 баллов)
Решение
1. Первый алгоритм хорошо
известен под названием сортировки слиянием.
Его основная идея заключается в том, что
имеются два указателя (i, j), каждый из
которых движется по своему подмассиву. Для
определенности будем считать, что i
пробегает нечетные номера, а j — четные.
Основной шаг алгоритма состоит в
том, что сравниваются X[i] и X[j].
Меньшее из двух чисел выводится в выходную
строку. После чего соответствующий
указатель смещается с шагом 2 дальше по своему
подмассиву.
Следует отдельно оговорить
ситуацию, когда один из указателей
пробегает свой подмассив полностью. В этом
случае остается переписать оставшуюся
часть другого подмассива целиком в выходную
строку.
2. Переписывая предыдущий
алгоритм в новом варианте, мы сталкиваемся
с необходимостью найти место для записи
меньшего из элементов: X[i] и X[j].
Пусть для определенности i < j.
Рассмотрим первый случай. Пусть X[i] £
X[j]. Тогда перемещаем i на две
позиции дальше и повторяем основной шаг
алгоритма. Если же при перемещении i
соответствующий подмассив будет исчерпан,
то закончена работа и всего алгоритма.
Второй случай сложнее и
интереснее: X[i] > X[j] — тогда
меняем элементы X[i] и X[j] местами и сдвигаем
индекс i на две позиции дальше.
Но сейчас упорядоченность
подмассива с четными номерами нарушена.
Восстанавливая порядок, будем сдвигать
элемент X[j] вправо по нечетному
подмассиву до тех пор, пока правее него находится
меньший элемент либо пока не закончится
весь подмассив.
Ниже приведен соответствующий
алгоритм. Здесь a — сортируемый массив, n
— его размер, temp(k) — вспомогательная
процедура для сдвига элемента a[k]
внутри соответствующего подмассива до
нужного места, ch(x, y) — процедура обмена
значениями величин x и y.
procedure Sort;
var i,j,k:integer;
x:integer;
procedure Temp(k:integer);
var p:boolean;
begin
if k+2<=n
then p:=a[k+2]<a[k]
else p:=false;
while p do
begin
ch(a[k],a[k+2]);
k:=k+2;
if k+2<=n
then p:=a[k+2]<a[k]
else p:=false
end
end;
begin
i:=1; j:=2;
while (i<=n) and (j<=n) do
begin
if i<j
then
begin {i левее j}
if a[j]<a[i] then
begin
ch(a[i],a[j]);
Temp(j)
end;
i:=i+2
end
else
begin {j левее i}
if a[i]<a[j] then
begin
ch(a[i],a[j]);
Temp(i)
end;
j:=j+2
end
end
end;
17. Найди меня (6 баллов)
Решение
Многие из нас использовали
описанные в задаче телефонные аппараты, но
не многие задумывались о назначении
латинских букв, которыми помечены цифровые
клавиши.
Известно, что в фирме Bell Labs
эксплуатируется подобная справочная
служба (см.: Д.Бентли. “Жемчужины творчества
программистов”).
Можно предположить, что
латинские буквы надписаны на кнопках
телефонных аппаратов в соответствии с
некоторыми общепринятыми стандартами, что
позволяет различным компаниям или регионам
создавать свои автоматизированные
справочные службы.
Тот факт, что в этом перечне
отсутствуют буквы “Q” и “Z”, видимо,
объясняется тем, что в английском языке эти
буквы наиболее редки (автор провел
небольшое исследование и может говорить об
этом с достаточной уверенностью).
Перейдем к собственно задаче.
Понятно, что разные фамилии могут
кодироваться одними и теми же наборами цифр
(в книге Бентли говорится, что таких совпадений
не более 0,2%). Такие совпадения в теории
называются коллизиями, или конфликтами.
Методы борьбы с коллизиями следующие.
1. Можно сформировать базу данных,
куда наряду с фамилией, именем и телефонным
номером абонента заранее включить его код
— цифровой аналог фамилии. Записи в такой
базе данных должны быть упорядочены по
кодам фамилий. Тогда будет возможно
организовать достаточно быстрый поиск
абонента. Правда, найдя абонента с заданным
кодом, придется проверить записи выше и
ниже найденной, чтобы установить всех
абонентов с таким кодом.
2. Второй вариант заключается в
том, чтобы разделить коды фамилий и данные о
самих абонентах. Представим себе две
таблицы: в первой хранятся упорядоченные по
возрастанию коды фамилий (каждый код
представлен ровно одной записью), во второй
таблице хранятся данные об абонентах,
расположенные группами.
Каждая группа второй таблицы
содержит сведения обо всех абонентах, чьи
коды совпадают. Каждая строка первой
таблицы содержит, кроме кода, ссылку (адрес)
на начало соответствующей группы во второй
таблице.
| Kод | Ссылка |
| ... | ... |
| ... | ... |
| 56884 | k |
| 56885 | k + 2 |
| ... | ... |
| Номер записи | Фамилия абонента | Имя | Телефон | Адрес |
| ... | ... | ... | ... | ... |
| k | Knuth | Donald | 2222222 | USA |
| k + 1 | Kmuth | Nick | 3333333 | France |
| k + 2 | Jovul | Mike | 4444444 | Germany |
| ... | ... | ... | ... | ... |
18. Алгоритм (2 балла)
Решение
Безусловно, это самое простое
задание олимпиады. Здесь ожидались два типа
ответов.
1. Данный алгоритм вычисляет R
= —B/A, если A ¹
0, или печатает слово “нет”, если… (то есть
далее следовало просто “озвучивание”
алгоритма). Формально такой ответ
правильный, но не содержательный.
2. Данный алгоритм вычисляет
корни уравнения A • R + B = 0.
Интересно, что некоторые
учащиеся не ожидали от жюри такого простого
задания и писали, что в данном случае
находится ненулевой корень уравнения A •
R • R + B • R = 0. Понятно, что
такой ответ жюри не устраивал.
РЕШЕНИЯ ЗАДАЧ ПРАКТИЧЕСКОГО ТУРА
Задачи практического тура предполагают написание программ, тексты которых у участников, как правило, достаточно велики. Авторские тексты гораздо скромнее, но все же занимают много места. Поэтому здесь приводятся только некоторые из программ.
1. Игра “Ним” (18 баллов)
Игра “Ним” хорошо известна и подробно описана в литературе. Легко заметить, что один из игроков может добиться того, что сумма двух последовательных ходов его и соперника всегда может равняться величине (N + 1). Отсюда следует, что необходимо разделить значение M на “порции” по (N + 1). Первый ход должен равняться оставшемуся от такого деления остатку.
Пример
Пусть M = 22, N = 4.
Тогда (N + 1) = 5, M mod (N + 1) =
22 mod 5 = 2. Отсюда следует, что при
правильной игре выигрывает первый игрок,
для этого он называет первым ходом число 2.
Далее первый игрок на всякий ход второго
отвечает дополнением до 5. Вот возможный
порядок ходов (жирным шрифтом выделены ходы
первого игрока): 2, 3, 2, 4, 1, 1, 4,
2, 3. Последним ходом достигается сумма 22,
и первый игрок побеждает.
2. Игра “Супер-Ним” (33 балла)
Пусть b — ход игрока, а S — сумма всех названных чисел. В таблице показаны все возможные клетки-пары (b, S) при Max = 20. Знаком “+” помечены выигрышные состояния.
| S \ b | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | ||||||
| 2 | + | |||||
| 3 | ||||||
| 4 | + | |||||
| 5 | ||||||
| 6 | + | |||||
| 7 | + | + | + | |||
| 8 | ||||||
| 9 | ||||||
| 10 | + | + | ||||
| 11 | ||||||
| 12 | + | |||||
| 13 | + | |||||
| 14 | + | |||||
| 15 | + | + | + | |||
| 16 | ||||||
| 17 | + | |||||
| 18 | ||||||
| 19 | ||||||
| 20 | + | + | + | + | + | + |
| 21 | + | + | + | + | + | |
| 22 | + | + | + | + | ||
| 23 | + | + | + | |||
| 24 | + | + | ||||
| 25 | + |
Если своим ходом игрок попадает
в выигрышную клетку, то при правильной
дальнейшей игре он может перемещаться
только по выигрышным клеткам и гарантированно
выиграет партию.
Знаки “+” здесь расставлены
таким образом, чтобы при любом ходе из такой
клетки соперник не мог попасть в другую
клетку “+”. И, наоборот, из любой не
помеченной клетки всегда можно за один ход
попасть в выигрышную клетку.
Пример
Пусть первые два хода
были такими (в скобках указаны ход и сумма
нарастающим итогом): (1, 1), (2, 3). Судя по
таблице, клетка (2, 3) не является выигрышной.
Следовательно, следующим ходом можно
перейти в выигрышное состояние. Это можно
сделать, выбрав ход (1, 4). Покажем, как
может развиться борьба дальше: (1, 5), (2, 7),
(3, 10), (4, 14), (4, 18), (3, 21).
Построение таблицы можно
выполнить, двигаясь от ее конца к началу.
Второй вариант решения задачи — это
построение рекурсивного алгоритма.
Ниже приведен пример рекурсивной
программы.
Программа 1
{$B-}
{ Неполное вычисление логического
выражения потребуется при вызове функции
Move }
Program SuperNim;
{ Игрок, набравший своим ходом сумму Мах,
выигрывает партию!}
Const Max=45;
Var h, S, D : integer; { h - ход, S - сумма
}
{ Основная процедура проверки
данной комбинации (h,S) }
Function Move(h, S : integer):boolean;
begin
{ Сначала считаем,
что ситуация выигрышная. Если же окажется,
что партия еще не закончена и соперник
найдет выигрыш в одном из вариантов
продолжения, то определим исходную
комбинацию как проигранную. }
Move:=True;
if S<Max then
if Move(h,S+h)
or Move(h+1,S+h+1)
or ((h>1) and Move(h-1,S+h-1))
then Move:=False
end;
Begin
h:=1;
S:=1;
{ пусть первый ход сделал человек
}
repeat
{ поиск хода
компьютером }
D:=-2; if h=1 then D:=-1;
repeat
{
Проверяется приращение хода D. Поиск
прекращается либо потому, что найден
выигрышный ход, либо проверено последнее
допустимое приращение D=1}
D:=D+1;
h:=h+D;
until Move(h,S+h) or (D=1);
{ выполняется
выбранный ход }
S:=S+h;
writeln(h:2,S:4);
{ надо ли еще ходить
человеку? }
if S<Max then
begin
readln(h);
S:=S+h;
writeln(h:2,S:4)
end;
until S>=Max { условие прекращения
партии}
End.
5. Упрощение выражения
Эта задача, понятная с первого
взгляда, содержит несколько достаточно
сложных для реализации этапов: контроль
корректности выражения, контроль корректности
скобочной структуры, определение для
каждого из операндов его положения (числитель
или знаменатель), формирование итоговой
строки.
Авторское решение основано на
следующей идее:
· для
анализа корректности проверяется
допустимость пар последовательных
символов;
· для
задания каждого из допустимых символов
входной строки используется перечислимый
тип sym;
· для
анализа корректности скобок используется
стек;
· в стеке
фиксируется текущий уровень (числитель или
знаменатель), который восстанавливается
при закрытии соответствующей скобки;
· для
формирования итоговой дроби используется
массив всех возможных переменных, где
хранятся степени каждой из них.
Ниже приведен полный текст
программы с комментариями.
Программа 2
{(c) В.Пинаев, 2000 г.
Рыбинская городская олимпиада по
информатике.
Первая задача практического тура.
"Упрощение выражения"}
Program Task1;
Const T=True;
F=False; {обозначения
для краткости}
Type sym=(oper, ident, l_parent, r_parent, start, stop);
{
перечислимый тип (то, что анализируется в
выражении): знак операции, идентификатор
переменной, левая и правая скобки,
состояния начала и конца строки }
Const tabl : array [sym, sym ] of boolean =
((F,T,T,F,F,F), {таблица корректности:}
(T,F,F,T,F,T), {tabl[i,j]=true, если }
(F,T,T,F,F,F),
{за символом i может следовать
символ j }
(T,F,F,T,F,T),
{например, tabl[oper,ident]=true, так как}|
(F,T,T,F,F,F), {за знаком операции}
(F,F,F,F,F,F));
{может следовать идентификатор}
Type stack = array [0..255] of -1..1;
{стек для левых скобок с
фиксацией уровня выражения "верх - низ":
-1 - знаменатель, 1 - числитель }
Var st: stack;
s : string;
sm, sm_old: sym;
up: -1..1;
id: array['A'..'Z'] of integer;
{таблица степеней
идентификаторов}
Error:boolean; {признак ошибки}
n, i : integer;
c:char;
top:byte;
Procedure Init; { процедура инициализации }
var c:char;
begin
sm_old:=start; { предыдущий символ }
sm:=stop; { текущий символ }
up:=1; { указатель "верх - низ",
пока мы в числителе}
top:=0; { указатель на вершину стека}
st[0]:=1; { изначально мы находимся в
числителе}
Error:=F; { ошибка пока не обнаружена}
for c:='A' to 'Z' do
id[c]:=0; { степени всех
идентификаторов пока не нужны}
end;
Procedure Print;{ процедура вывода ответа}
var c:char;
k:integer;
p1,p2,t:string;
begin
p1:=''; { пока числителя нет}
p2:=''; { пока знаменателя нет}
k:=0; { кол-во
идентификаторов в знаменателе}
for c:='A' to 'Z' do
{перебираем все
идентификаторы}
begin
str(abs(id[c]),t);
{определяем степень идентификатора}
if abs(id[c])=1 then t:=c
{определяем, как записать идентификатор:}
else t:=c+'^'+t;
{со степенью или нет}
if id[c]>0 then
{определяем,
куда записать идентификатор}
if p1='' {нужен ли знак умножения?}
then p1:=t
else p1:=p1+'*'+t
else if id[c]<0 then
begin
if p2='' then p2:=t
else p2:=p2+'*'+t;
k:=k+1 { еще один идентификатор }
end
end;
if p1='' then p1:='1';
{ определяем формат вывода
}
if k=1 then p2:='/'+p2
else if k>1 then p2:='/('+p2+')';
writeln(p1+p2) { а вот и сам
вывод }
end;
Begin
assign(input,'input.txt');
assign(output,'output.txt');
reset(input);
rewrite(output);
readln(n);
{количество
анализируемых вариантов}
for i:=1 to n do
begin
Init;
while not
Error and not eoln do
begin {пока
нет ошибки и есть что читать }
read(c); { читаем очередной символ}
case c of { опознаем тип символа}
'A'..'Z' : begin
sm:=ident;
{учитываем в таблице идентификаторов
степень}
id[c]:=id[c]+up
end;
'*', '/' : begin
sm:=oper;
{через стек определяем "верх - низ"}
if c='/' then up:=-st[top]
else up:=st[top]
end;
'(' : begin {кладем скобку в стек}
sm:=l_parent;
{с признаком "верх - низ"}
inc(top);
st[top]:=up
end;
')' : begin
{снимаем скобку из стека}
sm:=r_parent;
{и определяем "верх - низ"}
if top>0 then
begin
up:=st[top];
top:=top-1;
end
else Error:=T
{или обнаружена ошибка}
end
else Error:=T
end;
{проверяем
допустимость следования символов}
Error:=Error
or not tabl[sm_old,sm];
if not Error
then sm_old:=sm
end;
readln;
{закончили чтение
текущей строки}
{если стек не пуст
или конец строки сейчас недопустим }
Error:=Error or (top<>0) or
not tabl[sm,stop];
if Error then writeln('ERROR')
{ то выводим ERROR }
else Print { иначе
печатаем выражение }
end
end.
6. Ломаная линия
Ниже приведено авторское решение.
Программа 3
{(c) В.Пинаев, 2000 г. Рыбинская городская
олимпиада по информатике. Вторая задача
практического тура. "Ломаная линия"}
Program Task2;
Const m_max=20;
Type arr=array[0..m_max,0..m_max] of
boolean;
Var t:arr;
{массив контроля занятых точек таблицы}
x,y,i,j,k,n,z,max:integer;
Error:string;
{результат анализа
ломаной}
WasError:boolean; {признак
ошибки}
Begin
WasError:=False;
assign(input,'input.txt');
reset(input);
readln(max,n);
assign(output,'output.txt');
rewrite(output);
for i:=0 to max do
for j:=0 to max do
t[i,j]:=False;
{помечаем
все незанятые точки таблицы}
t[0,0]:=True; { начало отсчета }
x:=0; { координаты начала ломаной}
y:=0;
Error:='нет'; { пока нет ошибок и нет
пересечения}
for i:=1 to n do
begin
readln(j); {
читаем размер звена}
if j>0
then z:=1 else z:=-1;
{фиксируем
направление}
j:=abs(j); {длина
звена}
if not WasError Then
begin
if i mod 2 =
0 then
{звено вертикальное}
begin
if ((y+j*z)>max) or ((y+j*z)<0) then
begin
Error:='ошибка';
{выход за пределы таблицы}
break
end;
for k:=1 to j do
begin {пересчет координат}
y:=y+z; {и проверка пересечения}
if t[x,y] then Error:='да';
t[x,y]:=True
end
end
else {звено
горизонтальное}
begin
if ((x+j*z)>max) or ((x+j*z)<0) then
begin
Error:='ошибка';
{выход за пределы таблицы}
break
end;
for k:=1 to j do
begin {пересчет координат}
x:=x+z; {и проверка пересечения}
if t[x,y] then Error:='да';
t[x,y]:=True
end
end
end;
WasError:=Error='ошибка';
end;
writeln(Error); {вывод
результата}
close(output);
close(input);
end.
7. Восстановление ошибок
Ниже приведено авторское решение.
Программа 4
{(c) В.Пинаев, 2000 г. Рыбинская городская
олимпиада по информатике. Третья задача
практического тура. "Восстановление
ошибок"}
Program Task3;
{ Декодирование по Р.Р. Варшамову и Г.М.
Тененгольцу. Раскодирование выполняется
прямым перебором. }
var fin,fout:text;
name,st,correct_st:string;
vr:integer;
s_vr:string;
s,i,j,w,l,m,n,s_mod_l,num,n_c:integer;
{ проверка дополнительного условия }
function Check(st:string; n:integer):boolean;
var s,i,l:longint;
Begin
s:=0; {сумма номеров
двоичных символов кодового слова st}
l:=n+1;
for i:=1 to length(st) do
if st[i]='1'
then
begin
inc(s,i); s:=s mod l end;
Check:=(n=length(st))and((s mod l)=
0);
End;
{ процедура исправления ошибок
Type_Error='E' - строка имеет нужную длину,
Type_Error='L' - строка короче,
Type_Error='G' - строка длиннее.
st - редактируемая строка,
c - исправленная строка,
num - количество таких строк (num=0 или num=1)
Доказано, что если строка исправима, то это
можно сделать только единственным способом.}
procedure Error(type_error:char; st:string;
var c : string;
var num :integer);
var fj,i,j,_s,l:integer;
t:string;
begin
num:=0;
l:=length(st);
case type_error of
'E': begin
for i:=1 to l do
begin
t:=st;
{пробуем замены 1 на 0}
if st[i]='1' then
begin
t[i]:='0';
if Check(t,n) then
begin
inc(num);
c:=t;
exit
end
end
end
end;
'G': begin
for i:=1 to l do
begin
t:=st;
{проверка удаления символа}
delete(t,i,1);
if Check(t,n) then
begin
inc(num);
c:=t;
exit
end
end
end;
'L': begin
for i:=1 to l+1 do
begin
t:=st;
{проверка вставки 1}
insert('1',t,i);
if Check(t,n) then
begin
inc(num);
c:=t;
exit
end;
t:=st;
{проверка вставки 0}
insert('0',t,i);
if Check(t,n) then
begin
inc(num);
c:=t;
exit;
end
end
end
end
end;
Begin
assign(input,'input.txt');
assign(output,'output.txt');
reset(input);
rewrite(output);
readln(n,m);
for i:=1 to m do
begin
readln(st);
n_c:=1;
{ если строка верная
}
if Check(st,n) then correct_st:=st
else
begin
{
корректировка "неверной" строки}
if
length(st)=n then begin
Error('E',st,correct_st,n_c)
end
else if
length(st)<n then
Error('L',st,correct_st,n_c)
else
Error('G',st,correct_st,n_c)
end;
{ если найден
вариант исправления }
if n_c = 1 then
{вывод
исправленной строки}
writeln(correct_st)
else writeln('ERROR')
end;
close(input);
close(output)
End.
Методические
рекомендации учителям
при подготовке олимпиад по информатике. Анализ
олимпиадных заданий
С целью получения достоверной
информации о качестве заданий олимпиады
автор практикует анкетирование как
учащихся, так и приглашенных учителей. Так,
в 2000 году всем желающим были предложены
анкеты, в которых предлагалось оценить
каждую из задач. Вопросы формулировались
так:
· отметьте
удачные, на ваш взгляд, задания олимпиады;
· отметьте
неудачные, на ваш взгляд, задания олимпиады.
Анкеты были выданы во время
разбора решений и были собраны после его
окончания. Акцент в анкете делался на
выделение самых запомнившихся задач.
Поэтому по некоторым задачам число голосов
значительно меньше, чем по другим. Анкеты
заполнялись анонимно. Всего было заполнено
36 анкет учащимися и 12 — педагогами.
Данные анкетирования
представлены в таблице 1.
Прямым жирным шрифтом в таблице
выделены самые удачные задачи (“Операция
над таблицей”, “Золотое дерево”).
Жирным курсивом показана
неудачная задача (“Испорченная связь”).
Таблица 1
| Задание | Категория анкетируемых | Всего голосов | Разность: "за" и "против" | ||||
| Учащиеся | Педагоги | за | против | ||||
| за | против | за | против | ||||
| Операция над таблицей | 23 | 4 | 9 | 0 | 32 | 4 | 28 |
| Питон | 16 | 14 | 6 | 3 | 22 | 17 | 5 |
| Ворона и сыр | 23 | 13 | 4 | 6 | 27 | 19 | 8 |
| Золотое дерево | 25 | 9 | 11 | 0 | 36 | 9 | 27 |
| Испорченная связь | 15 | 18 | 4 | 4 | 19 | 22 | -3 |
| Пропущенное число | 21 | 7 | 10 | 0 | 31 | 7 | 24 |
| Сортировка | 21 | 7 | 9 | 2 | 30 | 9 | 21 |
| Найди меня | 22 | 13 | 3 | 7 | 25 | 20 | 5 |
| Алгоритм | 13 | 15 | 7 | 0 | 20 | 15 | 5 |
| Всего анкет | 179 | 100 | 63 | 22 | 242 | 122 | 120 |
Вот основные результаты
анкетирования.
1. В целом набор задач можно
признать вполне удовлетворительным, так
как участникам предлагалось решить любые
четыре задачи на выбор, а за каждую из задач
проголосовали от 25 до 13 учащихся.
2. Так как по каждой задаче
достаточно много голосов “за”, то следует
признать набор задач в достаточной мере
разносторонним. Это обстоятельство
позволило каждому выбрать задачи по своему
вкусу.
3. Очень неприятной оказалась
задача на комбинаторику и системы
счисления (“Испорченная связь”). По мнению
автора, это объясняется следующими
причинами: теме “Системы счисления”
уделяется мало внимания в школьном курсе
информатики, условие задачи было
сформулировано недостаточно четко, решение
оценивалось малым количеством баллов.
4. Задача “Алгоритм” оценена
участниками не очень высоко, так как за ее
очень простое решение предлагалось целых 2
балла. В то же время оценка педагогов по
этой задаче очень высокая, что означает их
желание всегда иметь на олимпиадах наряду
со сложными и простые задачи, тогда есть
надежда, что всякий участник сможет решить
хотя бы одну задачу.
5. Анкетирование среди педагогов
по задаче “Найди меня” было проведено без
разбора с ними ее решения. Вероятно, поэтому
задача получила целых 7 (!) голосов “против”.
Эта же задача у учащихся получила
достаточно высокую отметку: +22 — 13 = +9.
6. Соотношение анкет “за” и анкет
“против” у педагогов примерно составляет
отношение 3:1, в то же время этот показатель у
учащихся равен 8:1. Если предположить, что
экспертная оценка педагогов более
объективна, то итоги анкетирования
настораживают: следует более серьезно
заниматься с учащимися олимпиадной
подготовкой.
Выводы. Таким образом, анкетирование показало, что набор задач олимпиады был сформирован достаточно удачно и охватывал разнообразные темы. В то же время если бы не было разбора задач как с учащимися, так и с педагогами, то идеи задач олимпиады могли бы остаться непонятыми, неоцененными и были бы невостребованы.
После олимпиады 1999 года автор
также проводил исследование заданий,
сравнивая полученные учащимися оценки с их
же экспертной оценкой.
При голосовании “за” или “против”
разрешалось указывать не более трех
заданий. Кроме собственно анкетирования,
был проведен анализ решений задач, что
позволило сравнить объективные данные о
решениях задач с экспертной оценкой этих
заданий самими учащимися.
Результаты этого исследования
представлены в таблице 2. Самая удачная
задача — “Автомат”, а самая неудачная — “Принцы
в лабиринте”.
Таблица 2
|
Характеристики |
Задачи |
||||||||
| Алго- ритм | Таб- лица | После- дова- тель- ность | Оклеи- вание лаби- ринта | Азбука морзе | Разбие- ние на пары | Принцы в лабири- нте | Формат PCX | Автомат | |
| Количество положительных решений | 22 | 13 | 54 | 35 | 16 | 39 | 2 | 12 | 13 |
| Максимальный балл по задаче | 5 | 2 | 7 | 3 | 4 | 9 | 9 | 6 | 10 |
| Средний балл | 3,4 | 1,7 | 3,3 | 1,7 | 2,3 | 2,8 | 0,5 | 1,9 | 8,8 |
| Процент от максимальной оценки | 67,7 | 86,5 | 46,4 | 57,6 | 56,3 | 31,1 | 5,6 | 31,9 | 87,7 |
| Сумма набранных баллов по задаче | 74,5 | 22,5 | 175,5 | 60,5 | 36 | 109 | 1 | 23 | 114 |
| Подано голосов "за" | 12 | 12 | 29 | 26 | 19 | 12 | 5 | 10 | 38 |
| Подано голосов "против" | 5 | 2 | 2 | 4 | 6 | 6 | 31 | 11 | 1 |
В результате проведенных
исследований могут быть сформулированы
требования к методике составления
олимпиадного задания и общие правила
проведения олимпиады:
· задание
должно иметь порядковый номер и
запоминающееся название;
· в задании
следует указать максимальную оценку в
баллах;
· если в
задании формулируется несколько вопросов,
то необходимо указать баллы по каждому из
них;
· следует
разделить тексты условия и самого вопроса;
· вопрос
задания должен следовать в конце текста;
· если в
качестве решения предполагается найти
эффективный алгоритм, то необходимо об этом
прямо написать в тексте задания, указав
критерий оптимальности;
· необходимо
четко выделить входные и выходные данные,
указав предполагаемые ограничения;
·
целесообразно привести один или несколько
примеров задания входных и выходных данных;
· текст
задания должен располагаться на одной
стороне листа;
· на
практическом туре необходимо точно
сформулировать формат входных и выходных
данных;
· на бланке с
текстами заданий целесообразно указать
выдержки из регламента олимпиады;
· для заданий
практических туров нужно обязательно
указать время решения одного теста и
характеристики тестирующего компьютера;
· задания не
должны предполагать большого ручного счета
и применения громоздких формул;
· не
рекомендуется предлагать на олимпиаде для
решения более 4—5 заданий на теоретическом
туре и 1—2 заданий на практическом туре;
· время
проведения теоретического тура не должно
превышать 3 часов, а практического тура — 4
часов;
· не следует
на олимпиадах по информатике
ограничиваться проведением только либо
одного теоретического, либо одного
практического тура;
· в плане
проведения олимпиады обязательно должен
быть предусмотрен разбор решений.
Методика проверки решений задач теоретического тура
Автором на практике
использовалась следующая методика
проверки задач.
При анализе условия задачи
определялись возможные пути ее решения.
Каждому из найденных вариантов ставилось в
соответствие определенное количество
баллов.
Например, если в задаче
говорилось об отыскании эффективного по
использованию памяти алгоритма, то
неэффективные алгоритмы заранее
оценивались меньшим количеством баллов.
Дополнительно предусматривалось
введение поощрительных и штрафных баллов
за те или иные особенности решения.
Разработанная по каждой задаче
методика оценивания обсуждалась с
учителями. При проверке решений член жюри
руководствовался именно этой методикой.
Причем проверяющий должен был указывать в
листе с решением, за что он снял или добавил
баллы.
В качестве примера приведем
методику проверки задания “Автомат”:
· 4 балла — за
полную расшифровку текста “Ехали медведи
на велосипеде…”,
· 2 балла — за
частично расшифрованный текст,
· 6 баллов —
за правильное описание работы автомата,
· 3 балла — за
описание алгоритма Хаффмана без применения
схемы работы автомата (под схемой работы
автомата понимается описание следующего
рода: по текущему состоянию и текущему
входному символу-биту определяется новое
состояние или выводится расшифрованный
символ),
· 3 балла — за
сведение управляющей таблицы автомата к
дереву Хаффмана,
· —1 балл — за
отсутствие явного указания о переходе
автомата в нулевое состояние после вывода
очередного символа,
· 1 балл — за
абстрактное описание алгоритма Хаффмана (общие
рассуждения, не связанные с данной
конкретной задачей).
Отметим еще раз, что проведение
теоретического тура позволяет выделить
сильных учащихся, представивших даже
неполные решения.
Методика проверки решений задач практического тура
Методика проверки решения
задач практического тура принципиально
отличается от методики проверки задач
теоретического тура. Как и прежде, методика
проверки определяется по каждой задаче
заранее.
Автор задачи заранее готовит
набор тестов. Каждому тесту ставится в
соответствие весовое значение в баллах. В
условии задачи указывается максимальная
оценка (сумма баллов по всем тестам). Жюри
может предусмотреть иной способ оценивания
сданного решения. Например, в методике
оценивания может быть предусмотрено, что
баллы за определенные тесты начисляются в
зависимости от результата выполнения
других тестов.
Следует избегать задач, в которых
количество возможных ответов невелико.
Пример
Пусть требуется проверить
правильность расстановки скобок в записи
некоторого арифметического выражения.
Требование “вывести сообщение о наличии
или отсутствии ошибки” явно неудачно, так
как возможны решения, в которых сообщение
выводится произвольным образом. Правильнее
было бы потребовать вывести сообщение и
указать место, где обнаруживается первая
ошибка.
Тесты по возможности должны
охватывать различные алгоритмы решения.
Пример
Если в некоторой задаче
возможно решение, ориентированное именно
на “перемешанные” исходные данные, то
целесообразно предложить тесты, в которых
исходные данные упорядочены.
В условии задачи обязательно
должен быть оговорен формат входных и
выходных данных.
Для задач практического тура
целесообразно оговорить предельные
размеры каждого из входных параметров и
время тестирования решения. Если входные
данные представляют собой множество
значений, размещенных в файле, то
необходимо оговорить предельные размеры
этого файла. Следует понимать, что никакое
тестирование не может гарантировать, что
все случаи будут учтены.
Подготовленные тесты могут быть
условно разбиты на группы и должны
учитывать следующие особенности:
·
демонстрационные тесты (приводятся в
условии задачи и могут быть предоставлены в
виде файлов),
· вырожденные
случаи (решение задачи не существует),
· граничные
случаи (входные данные принимают граничные
значения),
· входные
данные специального вида (например, входные
данные упорядочены),
· общие тесты,
· тесты на
эффективность,
· тесты на
формат входных и выходных данных (если в
условии задачи предусмотрены различные
форматы входных и выходных данных).
Регламент проведения Рыбинской городской олимпиады по информатике
1. Рыбинская городская
олимпиада по информатике проводится в два
тура — теоретический и практический,
которые назначаются в разные дни. Условия
задач одинаковы для учеников всех классов.
Работы участников до начала проверки
шифруются. Расшифровка работ проводится
после проверки всех решений. Итоги
олимпиады подводятся отдельно по каждой
параллели.
2. Первый тур — теоретический, он
считается отборочным к практическому туру.
На теоретическом туре предлагаются 7—10
задач. В зачет идут результаты по четырем
задачам, номера которых указывает сам
участник. Время решения задач
теоретического тура — 3 часа. На
теоретическом туре разрешается
пользоваться только письменными
принадлежностями.
По каждой задаче указывается
максимальное количество баллов. Порядок
решения задач не определяется.
Если участник в нарушение правил
не укажет номера задач, подлежащих проверке,
то из всех сданных им решений будут
проверены первые четыре (в порядке
увеличения номеров заданий).
Апелляция по теоретическому туру
проводится после практического тура. До
апелляции работы участникам не выдаются.
После апелляции работы могут быть переданы
участникам.
Количество участников,
допускаемых на практический тур,
определяется имеющимися техническими
возможностями.
3. Основные типы задач
теоретического тура.
·
Описать алгоритм. Решением задачи является
описанный любым способом алгоритм (алгоритмический
язык, блок-схема, словесное описание,
программа на языке программирования) с
обязательными комментариями и
обоснованием его конечности.
·
Определить назначение алгоритма или найти
закономерность. Решением задачи является
обоснованный ответ.
·
Доказать свойство алгоритма (конечность,
массовость, определенность). Решением
задачи является строгое доказательство.
4. На практическом туре
предлагаются 2—3 задачи. Каждый участник
сдает только одно решение и только одной
задачи. Время проведения практического
тура — 4 часа. На практическом туре
разрешается пользоваться только
письменными принадлежностями и
компьютером.
Каждому участнику
предоставляется право выбора (на основании
анкеты теоретического тура) типа
компьютера и языка программирования. По
каждой задаче указывается максимальное
количество баллов. Как правило,
максимальное количество баллов, которое
может набрать участник в практическом туре,
примерно равно максимальному количеству
баллов по четырем заданиям теоретического
тура.
Каждый участник практического
тура сдает лист тестирования, на котором
указаны фамилия и имя, учебное заведение и
номер задачи. В последующем на листе
тестирования проставляются итоги
практического тура, которые могут быть
основанием для апелляции участника. Кроме
того, участник копирует текст программы-решения
на дискету учителя.
Проверка решения проводится по
желанию участника в его присутствии по
заранее подготовленным и неизвестным
участникам “секретным” тестам. В каждом
задании указывается максимальное время
работы программы по одному тесту.
Тест может быть не засчитан по
следующей причине: неверный ответ, ошибка
времени исполнения, превышение лимита
времени, ошибка компиляции. Исправления в
решении при проведении тестирования не
допускаются.
Окончательная оценка по
практическому туру получается
суммированием оценок отдельных тестов (если
в правилах тестирования не будет
предусмотрено иное).
Апелляция по итогам
практического тура проводится сразу после
окончания тестирования.
5. Общий результат каждого
участника по двум турам определяется как
сумма его баллов по каждому из двух туров.
По результатам олимпиады жюри определяет
городскую сборную команду для участия в
областной олимпиаде.
6. После подписания протокола и
объявления итогов олимпиады их пересмотр
не допускается.
7. Регламент рассмотрен и принят
на методическом объединении учителей
информатики и вычислительной техники 26
декабря 1997 года, дополнен 24 декабря 1999 года.
Благодарности
Автор благодарен всем, кто
помогал ему готовить этот материал.
Невозможно перечислить всех учителей,
студентов и школьников, высказывавших
критические замечания по содержанию задач
и методике их оценивания. Бывало так, что
участники олимпиад находили более изящные,
более рациональные, чем у автора, решения.
Рукопись не появилась бы на свет, если бы не
было постоянной поддержки со стороны
методиста Управления по делам образования
и молодежи Шуваловой Светланы Олеговны.
Всем им большое спасибо.
Автор признателен своей дочери
Надежде и редактору Салковой Марине
Александровне, которые сделали много
ценных замечаний.
Автор отдает себе отчет, как
много еще можно было бы улучшить, и
обязуется это сделать в будущем.
Литература
1. Кирюхин В.М., Лапунов А.В.,
Окулов С.М. Задачи по информатике.
Международные олимпиады 1989—1996 гг. М.: ABF, 1996,
272 с.
2. Котов В.М., Волков И.А., Лапо А.И.
Методы алгоритмизации: Учебное пособие для
9-го класса общеобразовательной школы с
углубленным изучением информатики. Минск:
ИГП “Нар. асвета”, 1997, 160 с.
3. Окулов С.М., Пестов А.А., Пестов
О.А. Информатика в задачах. Киров: Изд-во
ВГПУ, 1998, 343 с.
4. Олимпиады по информатике-1999: Сб.
задач / Под ред. Н.Л. Андреевой. Саратов: Изд-во
Саратовского унта, 1999, 48 с.
5. Чернов А.В. и др. Московские
студенческие командные олимпиады по
программированию (сборник задач). М.: МГУ, 1999,
72 с./
6. Пинаев В.Н. Олимпиадные
задачи по программированию: Учебное
пособие / РГАТА. Рыбинск, 1997, 41 с.
7. Пинаев В.Н. Двенадцатая
городская олимпиада по программированию:
Учебное пособие / РГАТА. Рыбинск, 1998, 24 с.
8. Пинаев В.Н.
Четвертьфинальные соревнования
студенческого командного первенства мира
по программированию. Центральный регион
России / РГАТА. Рыбинск, 1999, 30 с.
9. Пинаев В.Н. Второй
молодежный чемпионат по информатике и
программированию / РГАТА. Рыбинск, 1998, 14 с.
10. Третий молодежный городской
открытый чемпионат по информатике и
программированию “ПИК-99”: Информационно-справочные
материалы / РГАТА. Рыбинск, 1999, 24 с.
11. Пинаев В.Н. “Квадратное
программирование”: идеи и решения. “Информатика”,
№ 43/2000.
12. Основные современные
концепции творчества и одаренности. / Под
ред. Д.Б. Богоявленской. М.: Молодая гвардия,
1997, 416 с.
13. Соколов В.Н. Педагогическая
эвристика: Введение в теорию и методику
эвристической деятельности: Учебное
пособие для студентов высших учебных
заведений. М.: Аспект Пресс, 1995, 255 с.
14. Доровской А.И.
Дидактические основы развития одаренности
учащихся. М.: Российское педагогическое
агентство, 1998, 210 с.
15. Волков И.П. Много ли в школе
талантов? М.: Знание, 1989, 80 с.
16. Гильбух Ю.З. Внимание:
одаренные дети. М.: Знание, 1991, 80 с.
17. Романовский И.В. Дискретный
анализ. Учебное пособие для студентов,
специализирующихся по прикладной
математике и информатике. СПб.: Невский
диалект, 1999, 254 с.
18. Бентли Д. Жемчужины
творчества программистов: Пер. с англ. М.:
Радио и связь, 1990, 224 с.
19. Андреева Е., Фалина И. Информатика:
Системы счисления и компьютерная
арифметика. М.: Лаборатория базовых знаний,
1999, 256 с.