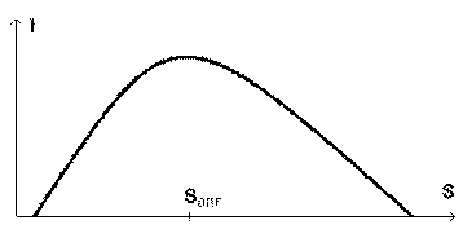
Профильная школа. ЭкзаменыПримерные ответы на профильные билетыЕ.А. Еремин, А.П. ШестаковПродолжение. Начало см. в № 19/2006 Билет № 31. Подходы к измерению информации. Преимущества и недостатки вероятностного и алфавитного подходов к измерению информации. Единицы измерения информации. Скорость передачи информации. Пропускная способность канала связиИнформация является важнейшим понятием и основным объектом изучения в информатике (см. билет № 1). Неудивительно поэтому, что проблема измерения информации имеет фундаментальное значение1. На бытовом уровне информация является синонимом слов сведения, знания, данные, новость, известие, сообщение и аналогичным им. При этом неявно подразумевается, что тот, кто получает информацию, выделяет из нее некоторый смысл (содержание). Смысловая составляющая информации во многом индивидуальна. Большинство россиян не способны извлечь никакой информации из текста на японском языке. Многие взрослые, взяв учебник для начальных классов, также не сочтут его заслуживающей своего внимания информацией, хотя, в отличие от предыдущего случая, понимают (слишком хорошо!), что там написано. Химика редко интересуют сообщения об археологических открытиях, а большая часть литераторов активно игнорирует любые сведения из области математики. Наконец, многие образованные люди не верят в статьи, опубликованные в бульварной прессе, заранее считая их недостоверными. Таким образом, информативность любых сведений и сообщений существенно зависит от воспринимающего их человека, его предыдущих знаний, опыта, интересов, отношения к источнику информации и множества других факторов личного характера, т.е. по своей сути является субъективной. Дополнительное пояснение. Во всех наиболее распространенных школьных учебниках подобными описаниями и несколькими несвязанными примерами неинформативных сообщений дело и ограничивается. Но на самом деле вопрос о соотношении между информативностью и предыдущими знаниями человека имеет самостоятельное значение. Например, в недавно вышедших учебниках [1, 2] приведен следующий весьма наглядный и любопытный качественный график зависимости воспринимаемой пользователем информации I от предварительно известных ему сведений S (для обозначения совокупности сведений, которыми располагает пользователь или любая другая система, принят специальный научный термин — тезаурус).
Из графика отчетливо видно, что воспринимаемая из фиксированного сообщения информация зависит от познаний пользователя неоднозначно. При малых S (тезаурус мал, пользователь неквалифицирован) воспринимаемая информация близка к нулю — человек ее просто не понимает. По мере роста S ситуация улучшается, и количество воспринятой из данного сообщения информации растет (невежественный пользователь быстро прогрессирует). Но лишь до определенного предела, а затем величина I начинает постепенно уменьшаться. Здесь вступает в действие другой фактор: при больших S (большой объем знаний, мы имеем дело с образованным пользователем) многие сообщения не могут добавить к тезаурусу ничего нового и их информативность вновь устремляется к нулю. Выражаясь житейским языком, когда человек много знает, его ничем не удивишь. Таким образом, график количества воспринимаемой информации имеет максимум (на рисунке он обозначен Sопт), соответствующий вполне определенному соотношению между содержащейся в сообщении информацией и уже имеющимися у субъекта знаниями2. Если задуматься над сутью рассмотренного графика, то можно получить целый ряд практически интересных выводов. Например, что передаваемая информация должна определенным образом соотноситься с уже имеющимися в ее приемнике сведениями, иначе данные могут оказаться бесполезными и только напрасно будут загружать каналы связи и узлы обработки. Между прочим, учащиеся после этих рассуждений должны проникнуться еще большим уважением к учителю, который постоянно вынужден “подстраивать” степень информативности своего рассказа, интуитивно оценивая разнообразные объемы тезаурусов сидящих в классе учеников, причем с учетом возможности их интеллектуального роста по мере освоения материала. Несколько иная трактовка измерения смысла сообщений по способу А.Н. Колмогорова весьма просто и интересно обсуждается в школьном учебнике [3]. Таким образом, субъективный характер восприятия информации делает однозначное измерение количества информации весьма затруднительным. Заметим, что современным компьютерам смысл обрабатываемых данных вообще принципиально недоступен, что делает еще более призрачной надежду на решение проблемы автоматического измерения “количества” содержания, которое в этих данных заключено. Как же все-таки измерить информацию? Общепринятым на данный момент решением проблемы является измерение объема информации при полном игнорировании ее смысла. Такой подход, несмотря на кажущуюся бессмысленность, оказывается необычайно полезным и широко применяется на практике. Действительно, в целом ряде важных практических задач смысл информации и даже ее вид (числа, текст, видео) несущественен. Например, при передаче информации по каналам связи, при распределении объемов ОЗУ для хранения различных типов данных, при записи информации на внешние носители, при архивации и многих других компьютерных применениях содержание передаваемой и обрабатываемой информации особого значения не имеет. Нечто похожее наблюдается и в “некомпьютерных” областях. Так, книги хранятся и ищутся не по содержанию, а по другим, часто весьма формальным признакам; в библиотеке нашего университета, в частности, книги расставлены на стеллажах в том числе с учетом размера обложки, который явно слабо связан с содержанием книги. Аналогично почтальону должно быть все равно, что именно находится внутри доставляемого им конверта, а диктор телевидения не может пропускать отдельные новости или их фрагменты в соответствии со своими личными убеждениями. Примечание. Подобно тому, как в физике при полном игнорировании трения можно установить фундаментальные законы движения, можно надеяться, что изучение “информации без смысла” позволит понять наиболее важные закономерности протекания информационных процессов. На этих и многочисленных подобных примерах мы видим, что информация перестает зависеть от человека при абстрагировании от ее смысла. Следовательно, появляется возможность объективного измерения количества информации. При этом используется два подхода: вероятностный или алфавитный. Вероятностный подход к измерению информацииЛюбая информация может рассматриваться как уменьшение неопределенности наших знаний об окружающем мире (в теории информации принято говорить именно об уменьшении неопределенности, а не об увеличении объема знаний). Математически это высказывание эквивалентно простой формуле I = H1 – H2 где I — это количество информации, а H1 и H2 — начальная и конечная неопределенность соответственно (очевидно, что H1 l H2). Величину H, которая описывает степень неопределенности, в литературе принято называть энтропиRей. Важным частным случаем является ситуация, когда некоторое событие с несколькими возможными исходами уже произошло, а, значит, неопределенность его результата исчезла. Тогда H2 = 0 и формула для информации упрощается: I = H Таким образом, энтропия опыта равна той информации, которую мы получаем в результате его осуществления. И наоборот: информация, получаемая из опыта, может быть вычислена через его энтропию. Очевидно, что единицы измерения информации и энтропии совпадают. Вычисление энтропии при вероятностном подходе базируется на рассмотрении данных о результате некоторого случайного события, т.е. события, которое может иметь несколько исходов. Случайность события заключается в том, что реализация того или иного исхода имеет некоторую степень неопределенности. Пусть, например, абсолютно незнакомый нам ученик сдает экзамен, результатом которого может служить получение оценок 2, 3, 4 или 5. Поскольку мы ничего не знаем о данном ученике, то степень неопределенности всех перечисленных результатов сдачи экзамена совершенно одинакова. Напротив, если нам известно, как он учится, то уверенность в некоторых исходах будет больше, чем в других: так, отличник скорее всего сдаст экзамен на пятерку, а получение двойки для него — это нечто почти невероятное. Наиболее просто определить количество информации в случае, когда все исходы события могут реализоваться с равной долей вероятности. В этом случае для вычисления информации используется формула Хартли. В более сложной ситуации, когда исходы события ожидаются с разной степенью уверенности, требуются более сложные вычисления по формуле Шеннона, которую обычно выносят за рамки школьного курса информатики. Очевидно, что формула Хартли является некоторым частным случаем более общей формулы Шеннона. Формула Хартли была предложена в 1928 году американским инженером Р.Хартли. Она связывает количество равновероятных состояний N с количеством информации I в сообщении о том, что любое из этих состояний реализовалось. Наиболее простая форма для данной формулы записывается следующим образом: 2I = N Причем обычно значение N известно, а I приходится подбирать, что не совсем удобно. Поэтому те, кто знает математику получше, предпочитают преобразовать данную формулу так, чтобы сразу выразить искомую величину I в явном виде: I = log2 N Важный частный случай получается из приведенной формулы при N = 2, когда результатом вычисления является единичное значение. Единица информации носит название бит (от англ. BInary digiT — двоичная цифра); таким образом, 1 бит — это информация о результате опыта с двумя равновероятными исходами. Чем больше возможных исходов, тем больше информации в сообщении о реализации одного из них. Пример 1. Из колоды выбрали 16 карт (все “картинки” и тузы) и положили на стол рисунком вниз. Верхнюю карту перевернули (см. рисунок). Сколько информации будет заключено в сообщении о том, какая именно карта оказалась сверху?
Все карты одинаковы, поэтому любая из них могла быть перевернута с одинаковой вероятностью. В таких условиях применима формула Хартли. Событие, заключающееся в открытии верхней карты, для нашего случая могло иметь 16 возможных исходов. Следовательно, информация о реализации одного из них равняется I = log2 16 = 4 бита Примечание. Если вы не любите логарифмы, можно записать формулу Хартли в виде 2I = 16 и получить ответ, подбирая такое I, которое ей удовлетворяет. Пример 2. Решите предыдущую задачу для случая, когда сообщение об исходе случайного события было следующим: “верхняя перевернутая карта оказалась черной дамой”. Отличие данной задачи от предыдущей
заключается в том, что в результате сообщения об
исходе случайного события не наступает полной
определенности: выбранная карта может иметь одну
из двух черных мастей. I = H1 – H2 До переворота карты неопределенность (энтропия) составляла H1 = log2 N1 после него — H2 = log2 N2 (причем для нашей задачи N1 = 16, а N2 = 2). В итоге информация вычисляется следующим образом: I = H1 – H2 = log2 N1 – log2 N2 = log2 N1/N2 = log2 16/2 = 3 бита Заметим, что в случае, когда нам называют карту точно (см. предыдущий пример), неопределенность результата исчезает, N2 = 1, и мы получаем “традиционную” формулу Хартли. И еще одно полезное наблюдение. Полная информация о результате рассматриваемого опыта составляет 4 бита (см. пример 1). В данном же случае мы получили 3 бита информации, а оставшийся четвертый описывает сохранившуюся неопределенность выбора между двумя дамами черной масти. Алфавитный (объемный) подход к измерению информацииПомимо описанного выше вероятностного подхода к измерению информации, состоящего в подсчете неопределенности исходов того или иного события, существует и другой. Его часто называют объемным, и он заключается в определении количества информации в каждом из знаков дискретного сообщения с последующим подсчетом количества этих знаков в сообщении. Пусть сообщение кодируется с помощью некоторого набора знаков. Заметим, что если для данного набора установлен порядок следования знаков, то он называется алфавитом. Наиболее сложной частью работы при объемном измерении информации является определение количества информации, содержащейся в каждом отдельном символе: остальная часть процедуры весьма проста. Для определения информации в одном символе алфавита можно также использовать вероятностные методы, поскольку появление конкретного знака в конкретном месте текста есть явление случайное. Самый простой метод подсчета заключается в следующем. Пусть алфавит, с помощью которого записываются все сообщения, состоит из M символов. Для простоты предположим, что все они появляются в тексте с одинаковой вероятностью (конечно, это грубая модель3, но зато очень простая). Тогда в рассматриваемой постановке применима формула Хартли для вычисления информации об одном из исходов события (о появлении любого символа алфавита): I = log2 M Поскольку все символы “равноправны”, естественно, что объем информации в каждом из них одинаков. Следовательно, остается полученное значение I умножить на количество символов в сообщении, и мы получим общий объем информации в нем. Напомним читателям, что осмысленность сообщения в описанной процедуре нигде не требуется, напротив, именно при отсутствии смысла предположение о равновероятном появлении всех символов выполняется лучше всего! Примечание. Стоит знать, что описанный простой способ кодирования, когда коды всех символов имеют одинаковую длину, не является единственным. Часто при передаче или архивации информации по соображениям экономичности тем символам, которые встречаются чаще, ставятся в соответствие более короткие коды и наоборот. Мы здесь не будем рассматривать этот весьма интересный и практически важный вопрос. Желающие могут обратиться, например, к известному школьному учебнику информатики [4] (начиная со второго издания) или к более глубокому, но тоже достаточно понятному [5]. Можно показать, что при любом варианте кодирования
(чем экономичнее способ кодирования, тем меньше разница между этими величинами — см. пример 4, приведенный ниже). Пример 3. Определить информацию, которую несет в себе 1-й символ в кодировках ASCII и Unicode. В алфавите ASCII предусмотрено 256 различных символов, т.е. M = 256, а I = log2 256 = 8 бит = 1 байт В современной кодировке Unicode заложено гораздо большее количество символов. В ней определено 256 алфавитных страниц по 256 символов в каждой. Предполагая для простоты, что все символы используются, получим, что I = log2 (256 * 256) = 8 + 8 = 16 бит = 2 байта Пример 4. Текст, сохраненный в коде ASCII, состоит исключительно из арифметических примеров, которые записаны с помощью 10 цифр от 0 до 9, 4 знаков арифметических операций, знака равенства и некоторого служебного кода, разделяющего примеры между собой. Сравните количество информации, которое несет один символ такого текста, применяя вероятностный и алфавитный подходы.
Легко подсчитать, что всего рассматриваемый в задаче текст состоит из N = 16 различных символов. Следовательно, по формуле Хартли Iвероятностная = log2 16 = 4 бита В то же время, согласно вычислениям примера 3, для символа ASCII Iалфавитная = 8 бит Двукратный избыток при кодировании символов связан с тем, что далеко не все коды ASCII оказываются в нашем тексте востребованными. В то же время несложно построить вариант специализированной 4-битной кодировки для конкретной задачи4, для которого Iвероятностная и Iалфавитная окажутся равными. В порядке подведения итогов сравним
вероятностный и алфавитный подходы, как того
требует вопрос билета. Первый подход позволяет
вычислить предельное (минимально возможное) теоретическое
значение количества информации, которое несет
сообщение о данном исходе события. Второй —
каково количество информации на практике с
учетом конкретной выбранной кодировки. Очевидно,
что первая величина есть однозначная
характеристика рассматриваемого события, тогда
как вторая зависит еще и от способа кодирования:
в “идеальном” случае обе величины совпадают,
однако на практике используемый метод
кодирования может иметь ту или иную степень
избыточности. Примечание. В учебниках информатики обычно ограничиваются описанием обоих подходов и не производится их сравнение. Приведенное выше сопоставление авторы провели исходя из собственных представлений. Возможно, составители билетов имели в виду какие-либо еще преимущества и недостатки. Вопрос о единицах измерения информации уже возникал при обсуждении вероятностного и алфавитного подходов. В самом деле, трудно изложить способ измерения величины, не упоминая при этом о единицах ее измерения. Поэтому мы уже сформулировали выше, что с теоретической точки зрения 1 бит — это информация, которая сокращает неопределенность наших знаний вдвое (ответ на вопрос типа “да”/“нет”, наличие или отсутствие какого-либо свойства, четность числа и т.д.). С точки зрения практической реализации компьютерных устройств для обработки информации 1 бит — это отдельный двоичный разряд любого из таких устройств. Иначе говоря, в вычислительной технике бит служит конструктивной базой для построения всех цифровых двоичных устройств: регистров, сумматоров и т.п. Отсюда очевидно, что в теории информации количество бит может быть любым, в том числе дробным, в то время как в реальных устройствах оно обязательно целое. Бит, будучи минимально возможной
порцией информации в компьютере, довольно
маленькая единица измерения. Поэтому на практике
чаще всего используется другая единица, которая
называется 1 байт = Примечание. Даже логические переменные, для каждой из которых, казалось бы, достаточно 1 бита, обычно занимают в оперативной памяти полный байт (или иногда ради единообразия даже несколько байт, например, LongBool в Паскале). С целью получения шкалы для измерения объемов информации в широких пределах от байта с помощью стандартных приставок образуется целая система более крупных производных единиц: 1 килобайт = 1024 байта 1 мегабайт = 1024 килобайта 1 гигабайт = 1024 мегабайта и т.д. В отличие от общепринятой системы производных единиц (широко используемой, например, в физике) при пересчете применяется множитель 1024, а не 1000. Причина заключается в двоичном характере представления информации в компьютере: 1024 = 210, и, следовательно, лучше подходит к измерению двоичной информации. Научившись измерять количество информации, можно ставить вопрос, как быстро она передается. Величину, которая равна количеству информации, передаваемому за единицу времени, принято называть скоростью передачи информации. Очевидно, что если за время t по каналу связи передано количество информации I, то скорость передачи вычисляется как отношение I / t. Примечание. При практической работе с величиной скорости передачи информации следует очень внимательно относиться к тому, что именно понимается под передаваемой информацией I. В частности, в процессе передачи к собственно пользовательской информации может добавляться значительное количество служебных, вспомогательных данных: например, согласно сетевому протоколу UDP (User Datagram Protocol), который является некоторой разновидностью известного протокола TCP (Transmission Control Protocol), из 146 байт стандартного Ethernet-кадра 46 являются служебными [6]. Кроме того, непосредственно перед передачей данные могут сжиматься или шифроваться, что также повлияет на время их передачи. Скорость передачи данных нельзя сделать сколь угодно большой; ее предельная максимальная величина имеет специальное название — пропускная способность канала связи. Данная характеристика определяется устройством канала и, что не так очевидно, способом передачи сигналов по нему. Иными словами, для разных способов представления данных одна и та же линия связи может иметь разную пропускную способность. К.Шеннон в созданной им теории информации доказал, что достигнуть при передаче пропускной способности линии можно всегда и путем к этому является повышение эффективности кодирования. Более того, даже при наличии в канале шумов любого уровня всегда можно закодировать сообщение таким образом, чтобы не происходило потери информации [1, 5]. Обе величины — скорость передачи и пропускная способность — по определению измеряются в одних и тех же единицах, являющихся отношением единиц информации и времени: бит/с, байт/с, Кб/с и т.д. Дополнительное пояснение. Кроме того, существует еще одна родственная единица измерения параметров передачи — бод. Количество бод есть количество изменений информационного параметра в секунду. Скорость передачи в битах в секунду в общем случае не совпадает с количеством бод. В [1] приводится очень наглядный пример, когда скорость в бит/с втрое выше, чем число бод. “Если информационными параметрами являются фаза и амплитуда синусоиды, причем различают 4 состояния фазы (0, 90, 180 и 270) и два значения амплитуды, то информационный сигнал имеет восемь различимых состояний. В этом случае модем, работающий со скоростью 2400 бод (с тактовой частотой 2400 Гц), передает информацию со скоростью 7200 бит/с, так как при одном изменении сигнала передается три бита информации”. Возможно, кстати, и обратное соотношение между величинами в бит/с и бод; в частном случае они могут совпадать. В качестве примера типичных значений скоростей передачи данных в современных компьютерах ниже приводятся табл. 1 и 2, составленные на основе сведений из известной книги [7]. Таблица 1. Характеристики устройств внешней памяти
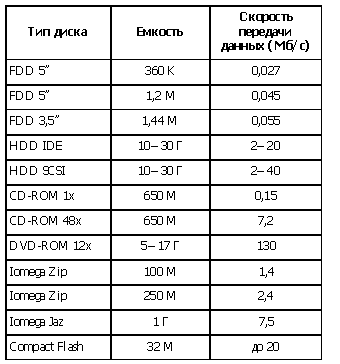
Таблица 2. Характеристики шин расширения
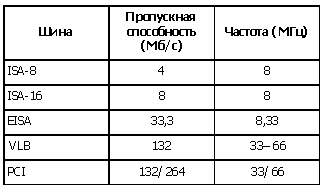
Примечание. Хотя проблема пропускной способности каналов связи весьма подробно излагается в специальной литературе, в доступных для учителей и школьников источниках она рассматривается не всегда, а если и рассматривается, то весьма поверхностно. Поэтому на экзамене, по мнению авторов, надо требовать от учеников знания только самых минимальных сведений. Расширенный материал в нашей публикации приведен исключительно для того, чтобы дать некоторую общую ориентировку учителям. Нам кажется, что это один из примеров, когда, прежде чем требовать знания вопроса от учащихся, стоит описать его на нужном уровне в школьных учебниках. Литература 1. Акулов О.А., Медведев Н.В. Информатика: базовый курс. М.: Омега-Л, 2005, 552 с. 2. Бройдо Э.А., Ильина О.П. Архитектура ЭВМ и систем. СПб.: Питер, 2006, 718 с. 3. Информационная культура: Кодирование информации, информационные модели. 9–10-е классы. М.: Дрофа, 2000, 208 с. 4. Семакин И.Г. Информатика. Базовый курс. 7–9-е классы / И.Г. Семакин, Л.А. Залогова, С.В. Русаков, Л.В. Шестакова. 2-е изд. М.: БИНОМ, 2004, 390 с. 5. Стариченко Б.Е. Теоретические основы информатики. М.: Горячая линия — Телеком, 2003, 312 с. 6. Никифоров С.В. Введение в сетевые технологии. М.: Финансы и статистика, 2003, 224 с. 7. Аппаратные средства IBM PC. Энциклопедия. / М.Гук. СПб.: Питер, 2003, 923 с. 2. С использованием электронной таблицы произвести обработку данных с помощью статистических функцийДаны сведения об учащихся класса, включающие средний балл за четверть, возраст (год рождения) и пол. Определить средний балл мальчиков, долю отличниц среди девочек и разницу среднего балла учащихся разного возраста. Решение Заполним таблицу исходными данными и проведем необходимые расчеты. В таблицу будем заносить данные из школьного журнала.
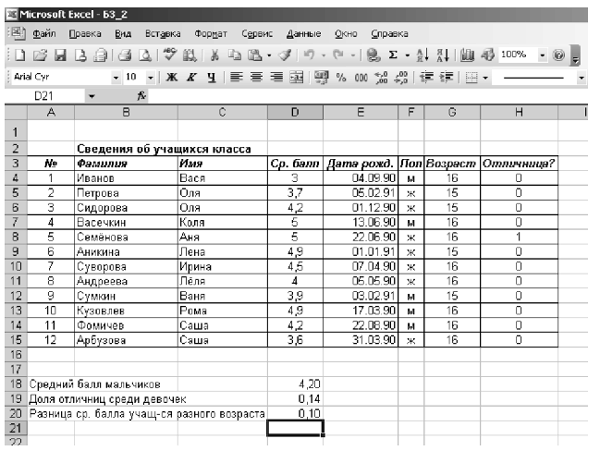
В таблице используются дополнительные колонки, которые необходимы для ответа на вопросы, поставленные в задаче (текст в них записан синим цветом), — возраст ученика и является ли учащийся отличником и девочкой одновременно. Для расчета возраста использована следующая формула (на примере ячейки G4): =ЦЕЛОЕ((СЕГОДНЯ()-E4)/365,25) Прокомментируем ее. Из сегодняшней даты вычитается дата рождения ученика. Таким образом, получаем полное число дней, прошедших с рождения ученика. Разделив это количество на 365,25 (реальное количество дней в году, 0,25 дня для обычного года компенсируется високосным годом), получаем полное количество лет ученика; наконец, выделив целую часть, — возраст ученика. Является ли девочка отличницей, определяется формулой (на примере ячейки H4): =ЕСЛИ(И(D4=5;F4="ж");1;0) Приступим к основным расчетам. Прежде всего требуется определить средний балл мальчиков. Согласно определению, необходимо разделить суммарный балл мальчиков на их количество. Для этих целей можно воспользоваться соответствующими функциями табличного процессора. =СУММЕСЛИ(F4:F15;"м";D4:D15)/СЧЁТЕСЛИ(F4:F15;"м") Функция СУММЕСЛИ позволяет просуммировать значения только в тех ячейках диапазона, которые отвечают заданному критерию (в нашем случае ребенок является мальчиком). Функция СЧЁТЕСЛИ подсчитывает количество значений, удовлетворяющих заданному критерию. Таким образом и получаем требуемое. Для подсчета доли отличниц среди всех девочек отнесем количество девочек-отличниц к общему количеству девочек (здесь и воспользуемся набором значений из одной из вспомогательных колонок): =СУММ(H4:H15)/СЧЁТЕСЛИ(F4:F15;"ж") Наконец, определим отличие средних баллов разновозрастных детей (воспользуемся в расчетах вспомогательной колонкой Возраст): =ABS(СУММЕСЛИ(G4:G15;15;D4:D15)/СЧЁТЕСЛИ(G4:G15;15)- СУММЕСЛИ(G4:G15;16;D4:D15)/СЧЁТЕСЛИ(G4:G15;16)) Таким образом, задача полностью решена. На рисунке представлены результаты решения для заданного набора данных. Варианты заданийС использованием электронной таблицы произвести обработку данных с помощью статистических функций. 1. Даны сведения об учащихся класса, включающие оценки в течение одного месяца. Подсчитайте количество пятерок, четверок, двоек и троек, найдите средний балл каждого ученика и средний балл всей группы. Создайте диаграмму, иллюстрирующую процентное соотношение оценок в группе. 2. Четверо друзей путешествуют на трех видах транспорта: поезде, самолете и пароходе. Николай проплыл 150 км на пароходе, проехал 140 км на поезде и пролетел 1100 км на самолете. Василий проплыл на пароходе 200 км, проехал на поезде 220 км и пролетел на самолете 1160 км. Анатолий пролетел на самолете 1200 км, проехал поездом 110 км и проплыл на пароходе 125 км. Мария проехала на поезде 130 км, пролетела на самолете 1500 км и проплыла на пароходе 160 км. Построить на основе вышеперечисленных данных электронную таблицу. · Добавить к таблице столбец, в котором будет отображаться общее количество километров, которое проехал каждый из ребят. · Вычислить общее количество километров, которое ребята проехали на поезде, пролетели на самолете и проплыли на пароходе (на каждом виде транспорта по отдельности). · Вычислить суммарное количество километров всех друзей. · Определить максимальное и минимальное количество километров, пройденных друзьями по всем видам транспорта. · Определить среднее количество километров по всем видам транспорта. 3. Создайте таблицу “Озера Европы”, используя следующие данные по площади (кв. км) и наибольшей глубине (м): Ладожское 17 700 и 225; Онежское 9510 и 110; Каспийское море 371 000 и 995; Венерн 5550 и 100; Чудское с Псковским 3560 и 14; Балатон 591 и 11; Женевское 581 и 310; Веттерн 1900 и 119; Боденское 538 и 252; Меларен 1140 и 64. Определите самое большое и самое маленькое по площади озеро, самое глубокое и самое мелкое озеро. 4. Создайте таблицу “Реки Европы”, используя следующие данные длины (км) и площади бассейна (тыс. кв. км): Волга 3688 и 1350; Дунай 2850 и 817; Рейн 1330 и 224; Эльба 1150 и 148; Висла 1090 и 198; Луара 1020 и 120; Урал 2530 и 220; Дон 1870 и 422; Сена 780 и 79; Темза 340 и 15. Определите самую длинную и самую короткую реку, подсчитайте суммарную площадь бассейнов рек, среднюю протяженность рек европейской части России. 5. В банке производится учет своевременности выплат кредитов, выданных нескольким организациям. Известна сумма кредита и сумма, уже выплаченная организацией. Для должников установлены штрафные санкции: если фирма выплатила кредит более чем на 70 процентов, то штраф составит 10 процентов от суммы задолженности, в противном случае штраф составит 15 процентов. Посчитать штраф для каждой организации, средний штраф, общее количество денег, которые банк собирается получить дополнительно. Определить средний штраф бюджетных организаций. 3. Решить текстовую логическую задачу (необходимо использовать не менее четырех переменных)Решить текстовую логическую задачу: Болельщики футбольных команд делали прогнозы об итогах соревнований “Турнир четырех”: — Я уверен, что “Спартак” будет чемпионом, а “ЦСКА” займет последнее место, — сказал Иван. — Что ты, “Спартак” выше третьего не поднимется, а “ЦСКА” станет вторым, — возразил Сергей. — Чемпионом будет “Динамо”, а “ЦСКА” войдет в тройку сильнейших, — сделал свой прогноз Петр. — “Динамо” будет вторым, а вот “Ротор” точно будет последним, — промолвил Алексей. Выяснилось, что каждый из болельщиков был прав в одном прогнозе и ошибся во втором. Как распределились места, занятые командами? Решение Решим задачу путем сопоставления высказываний и опираясь на информацию о том, что одно из них истинно, другое — ложно. Анализ начнем с последнего высказывания. Предположим, что высказывание “Ротор” займет 4-е место” истинно. Тогда “Динамо” будет вторым” — ложно (т.е. “Динамо” занимает 1-е или 3-е место). Пусть истинно высказывание “Динамо” займет первое место”, тогда ложно высказывание “ЦСКА” войдет в тройку сильнейших”, т.е. “ЦСКА” занимает 4-е место, но это место у нас уже занял “Ротор”. Поэтому эта цепочка рассуждений неверна. Следовательно, истинным будет высказывание “ЦСКА” займет 2-е или 3-е место”, а ложным — “Динамо” займет 1-е место”. Для “Динамо” осталась единственная возможность — 3-е место. Тогда далее высказывание “ЦСКА” станет вторым” истинно, а “Спартак” выше третьего не поднимется” — ложно. Таким образом, для “Спартака” остается единственная возможность — 1-е место, что не противоречит высказываниям Ивана, исходя из того, что одно из них истинно, другое — ложно. Таким образом, распределение мест: “Спартак” — I, “ЦСКА” — II, “Динамо” — III, “Ротор” — IV. Если отталкиваться от посылки, что истинно высказывание “Динамо” будет вторым”, ложно “Ротор” будет четвертым”, придем к противоречию (проделать рассуждения самостоятельно”. Варианты заданий1. Три подразделения — А, В, С — торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения: 1) А получит максимальную прибыль только тогда, когда получат максимальную прибыль В и С, 2) Либо А и С получат максимальную прибыль одновременно, либо одновременно не получат, 3) Для того чтобы подразделение С получило максимальную прибыль, необходимо, чтобы и В получило максимальную прибыль. По завершении года оказалось, что одно из трех предположений ложно, а остальные два истинны. Какие из названных подразделений получили максимальную прибыль? 2. Задача “Валютные махинации”. В нарушении правил обмена валюты подозреваются четыре работника банка — Антипов (А), Борисов (B), Цветков (С) и Дмитриев (D). Известно: 1) если А нарушил правила обмена валюты, то и В нарушил; 2) если В нарушил, то и С нарушил или А не нарушил; 3) если D не нарушил, то А нарушил, а С не нарушил; 4) если D нарушил, то и А нарушил. Кто из подозреваемых нарушил правила обмена валюты? 3. Задача “Пятеро друзей”. Пятеро друзей решили записаться в кружок любителей логических задач: Андрей (А), Николай (N), Виктор (V), Григорий (G), Дмитрий (D). Но староста кружка поставил им ряд условий: “Вы должны приходить к нам так, чтобы: 1) если А приходит вместе с D, то N должен присутствовать обязательно; 2) если D отсутствует, то N должен быть, а V пусть не приходит; 3) А и V не могут одновременно ни присутствовать, ни отсутствовать; 4) если придет D, то G пусть не приходит; 5) если N отсутствует, то D должен присутствовать, но это в том случае, если не присутствует V; если же и V присутствует при отсутствии N, то D приходить не должен, a G должен прийти”. В каком составе друзья смогут прийти на занятия кружка? 4. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники скрылись на синем “Бьюике”; Джонс сказал, что это был черный “Крайслер”, а Смит утверждал, что это был “Форд Мустанг” и ни в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет. Какого цвета и какой марки был автомобиль? 5. Для полярной экспедиции из восьми претендентов — А, В, С, D, Е, F, G и Н — надо отобрать шестерых специалистов: биолога, гидролога, синоптика, радиста, механика и врача. Обязанности биолога могут выполнять Е и G, гидролога — В и F, синоптика — F и G, радиста — С и D, механика — С и Н, врача — А и D. Хотя некоторые претенденты владеют двумя специальностями, в экспедиции каждый сможет выполнять только одну обязанность. Кого и кем следует взять в экспедицию, если F не может ехать без В, D — без С и без Н, С не может ехать одновременно с G, а A вместе с B? Билет № 41. Понятие алгоритма: свойства алгоритмов, исполнители алгоритмов. Автоматическое исполнение алгоритма. Способы описания алгоритмов. Основные алгоритмические структуры и их реализация на языке программирования. Оценка эффективности алгоритмов.Алгоритм — это понятное и точное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи или достижение указанной цели. Термин имеет интересное историческое происхождение. В IX веке великий узбекский математик аль-Хорезми разработал правила арифметических действий над десятичными числами. Совокупность этих правил в Европе стали называть “алгоризм”. Впоследствии слово трансформировалось до известного нам сейчас вида и, кроме того, расширило свое значение: алгоритмом стали называть любую последовательность действий (не только арифметических), которая приводит к решению той или иной задачи. Можно сказать, что понятие вышло за рамки математики и стало применяться в самых различных областях. Можно выделить три крупных разновидности алгоритмов: вычислительные, информационные и управляющие. Первые, как правило, работают с простыми видами данных (числа, вектора, матрицы), но зато процесс вычисления может быть длинным и сложным. Информационные алгоритмы, напротив, реализуют сравнительно небольшие процедуры обработки (например, поиск элементов, удовлетворяющих определенному признаку), но для больших объемов информации. Наконец, управляющие алгоритмы непрерывно анализируют информацию, поступающую от тех или иных источников, и выдают результирующие сигналы, управляющие работой тех или иных устройств. Для этого вида алгоритмов очень существенную роль играет их быстродействие, т.к. управляющие сигналы всегда должны появляться в нужный момент времени. Каждый алгоритм — это правила, описывающие процесс преобразования исходных данных в необходимый результат. Заметим, что данное важное свойство в некоторых книгах приводят как определение алгоритма. Для того чтобы произвольное описание последовательности действий было алгоритмом, оно должно обладать следующими свойствами. · Дискретность Процесс решения задачи должен быть разбит на последовательность отдельных шагов, каждый из которых называется командой. Примером команд могут служить пункты инструкции, нажатие на одну из кнопок пульта управления, рисование графического примитива (линии, дуги и т.п.), оператор языка программирования. Наиболее существенным здесь является тот факт, что алгоритм есть последовательность четко выделенных пунктов — такие “прерывные” объекты в науке принято называть дискретными. · Понятность Каждая команда алгоритма должна быть понятна тому, кто исполняет алгоритм; в противном случае эта команда и, следовательно, весь алгоритм в целом не могут быть выполнены. Данное требование можно сформулировать более просто и конкретно. Составим полный список команд, который умеет делать исполнитель алгоритма, и назовем его системой команд исполнителя (СКИ). Требование использовать при составлении алгоритмов только те команды, которые входят в СКИ, связано с тем, что исполнение алгоритма осуществляется формально, без возможности вникнуть в суть команд и проанализировать их. Одним из таких (вернее, основным из них) “бездушных” исполнителей является ЭВМ. Вообще ЭВМ является универсальным исполнителем алгоритмов. Это связано с тем, что любой алгоритм, составленный для ЭВМ, в конечном итоге транслируется в ее СКИ и, таким образом, становится доступным для исполнения. · Определенность (детерминированность) Команды, образующие алгоритм (или, можно сказать, входящие в СКИ), должны быть предельно четкими и однозначными. Их результат не может зависеть от какой-либо дополнительной информации извне алгоритма. Сколько бы раз вы не запускали программу, для одних и тех же исходных данных всегда будет получаться один и тот же результат. При наличии ошибок в алгоритме последнее сформулированное свойство может иногда нарушаться. Например, если не было предусмотрено присвоение переменной начального значения, то результат в некоторых случаях может зависеть от случайного состояния той или иной ячейки памяти компьютера. Но это, скорее, не опровергает, а подтверждает правило: алгоритм должен быть определенным, в противном случае это не алгоритм. Определенность также предполагает, что данные, необходимые для выполнения очередной команды алгоритма, получены на одном из предыдущих шагов алгоритма. · Результативность (конечность) Результат выполнения алгоритма должен быть обязательно получен, т.е. правильный алгоритм не может обрываться безрезультатно из-за какого-либо непреодолимого препятствия в ходе выполнения. Кроме того, любой алгоритм должен завершиться за конечное число шагов. Большинство алгоритмов данным требованиям удовлетворяют, но при наличии ошибок возможны нарушения результативности. · Корректность Любой алгоритм создан для решения той или иной задачи, поэтому нам необходима уверенность, что это решение будет правильным для любых допустимых исходных данных. Указанное свойство алгоритма принято называть его корректностью. В связи с обсуждаемым свойством большое значение имеет тщательное тестирование алгоритма перед его использованием. Как показывает опыт, грамотная и всесторонняя отладка для сложных алгоритмов часто требует значительно больших усилий, чем собственно разработка этих алгоритмов. При этом важно не столько количество проверенных сочетаний входных данных, сколько количество их типов. Например, можно сделать сколько угодно проверок для положительных значений аргумента алгоритма, но это никак не будет гарантировать корректную его работу в случае отрицательной величины аргумента. · Массовость Алгоритм имеет смысл разрабатывать только в том случае, когда он будет применяться многократно для различных наборов исходных данных. Например, если составляется алгоритм обработки текстов, то вряд ли целесообразно ограничивать его возможности только русскими буквами — стоит предусмотреть также латинский алфавит, цифры, знаки препинания и т.п. Тем более что такое обобщение особых трудностей не вызывает. Таковы основные свойства алгоритмов. Если их внимательно проанализировать, то становится очевидным, что исполнитель алгоритма не нуждается в какой-либо фантазии и сообразительности. Более того, для выполнения алгоритма совсем не требуется его понимание, а правильный результат может быть получен путем формального и чисто механического следования содержанию алгоритма. Из возможности формального исполнения алгоритма следует очень важное следствие: поскольку осознавать содержание алгоритма не требуется, его исполнение вполне можно доверить автомату или ЭВМ. Таким образом, составление алгоритма является обязательным этапом автоматизации любого процесса. Как только разработан алгоритм, машина может исполнять его лучше человека — быстрее и, что очень важно, не ошибаясь. Основными способами записи алгоритмов являются: · словесный; · словесно-формульный; · на алгоритмическом языке; · графический (блок-схема); · на языке программирования высокого уровня. Основными алгоритмическими структурами (ОАС) являются следование, развилка и цикл. В более сложных случаях используются суперпозиции (вложения) ОАС. Ниже приведены графические обозначения (обозначения на блок-схемах) ОАС.
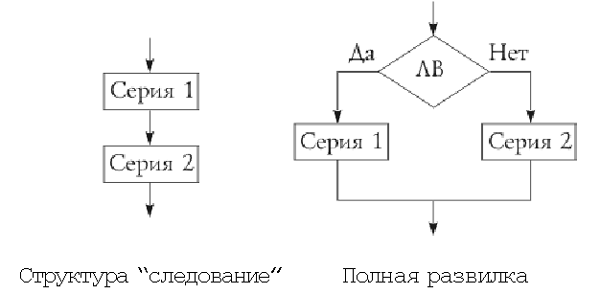
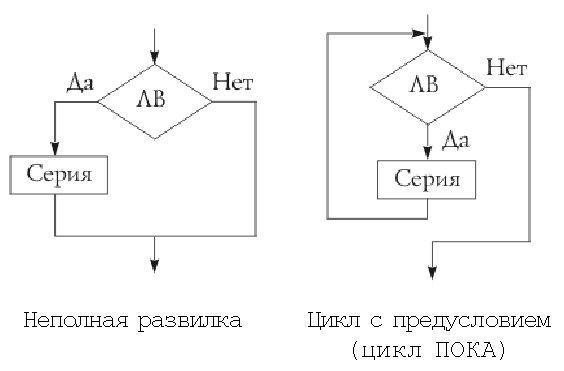
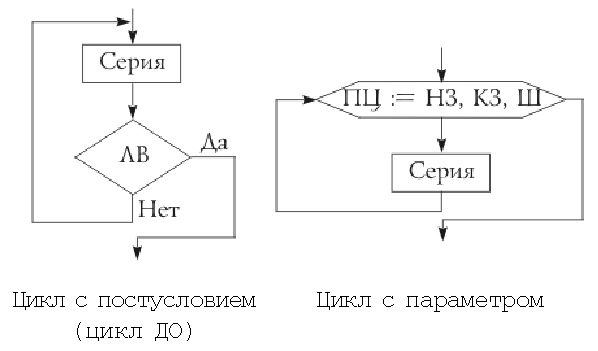
На схемах СЕРИЯ обозначает один или
несколько любых операторов; ЛВ — логическое
выражение (если его значение ИСТИНА, переход
происходит по ветви ДА, иначе — по НЕТ). На
схеме цикла с параметром использованы
обозначения: ПЦ — параметр цикла, Простейшие задачи имеют линейный алгоритм решения. Это означает, что такой алгоритм не содержит проверок условий и повторений, действия в нем выполняются последовательно, одно за другим, т.е. при его реализации используется структура “следование”. Чаще всего алгоритмы предполагают обработку некоторых величин. Величина — это элемент данных с точки зрения их смыслового (семантического) содержания или обработки. При разработке алгоритма данные можно разбить по смыслу на входные — аргументы, выходные — результаты, и промежуточные. Исходные (входные) — это данные, известные перед выполнением задачи, из условия. Выходные данные — результат решения задачи. Переменные, которые не являются ни аргументом, ни результатом алгоритма, а используются только для обозначения вычисляемого промежуточного значения, называются промежуточными. Чаще всего требуется указать имена и типы данных — целый, вещественный, логический и символьный, либо структурированный, базирующийся на одном из названных. Ветвления играют в алгоритмах очень большую роль, поскольку предусматривают корректную реакцию на самые разнообразные ситуации, возникающие в процессе обработки информации. Благодаря этой структуре алгоритм приобретает способность выбирать один из существующих вариантов работы, наиболее подходящий к сложившейся в данный момент ситуации. В частном случае речь может идти о выполнении или игнорировании при определенных условиях того или иного участка алгоритма. Значение ветвления в современном программном обеспечении трудно переоценить. Достаточно вспомнить стандартные элементы управления, такие, как меню, радиокнопки, флажки проверки или списки. Именно они дают возможность пользователю чувствовать себя за компьютером свободно и комфортно и выбирать те режимы работы, которые ему нужны. Приведем также полную форму ветвления в различных алгоритмических языках. QBasic IF <ЛВ> THEN операторы ELSE операторы ENDIF Pascal IF <ЛВ> THEN оператор ELSE оператор C if (<ЛВ>) оператор; else оператор; Очевидно, что запись отличается лишь незначительными второстепенными деталями. Для получения неполного ветвления ветвь “иначе” разрешается опускать. Достаточно часто при организации алгоритма решения задачи необходимо одну и ту же определенную последовательность команд выполнить несколько раз подряд. Конечно, самый простой способ — записать эти команды несколько раз друг за другом, и необходимое повторение действий будет организовано. Но как быть в тех случаях, когда количество команд, которые исполняются несколько раз, слишком велико? Или само количество повторений команд огромно? Или вообще неизвестно, а сколько же раз нужно повторить последовательность команд? Решить все эти проблемы можно, если использовать алгоритмическую структуру “цикл”. Командой повторения, или циклом, называется такая форма организации действий в алгоритме, при которой выполнение одной и той же последовательности команд повторяется до тех пор, пока истинно некоторое логическое выражение. Для организации цикла необходимо выполнять следующие действия: · перед началом цикла задать начальное значение параметров (переменных, используемых в логическом выражении, отвечающем за продолжение или завершение цикла); · внутри цикла изменять переменную (или переменные), которая сменит значение логического выражения, за счет которого продолжается цикл, на противоположное (для того чтобы цикл в определенный момент завершился); · вычислять логическое выражение — проверять условие продолжения или окончания цикла; · выполнять операторы внутри цикла; · управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из цикла в противном случае. Различают циклы с известным числом повторений (цикл с параметром) и итерационные (с пред- и постусловием). Опишем схематично, как выполняется каждый из циклов. Цикл с предусловием: а) вычисляется значение логического выражения; б) если значение логического выражения “истина”, переход к следующему пункту, иначе к п. д); в) выполняется тело цикла; г) переход к п. а); д) конец цикла. Цикл с постусловием: а) выполняется тело цикла; б) вычисляется значение логического выражения; в) если значение логического выражения “ложь”, переход к п. а), иначе к следующему пункту; г) конец цикла. Замечание. Таким образом, цикл с постусловием организован, в частности, в алгоритмических языках Pascal и QBasic. В языке C переход к повторению вычислений, как и в цикле с предусловием, осуществляется в случае истинности логического выражения. Цикл с параметром: а) вычисляются значения выражений, определяющие начальное и конечное значения параметра цикла; б) параметру цикла присваивается начальное значение; в) параметр цикла сравнивается с конечным значением; г) если параметр цикла превосходит (при положительном шаге) конечное значение параметра цикла (или, наоборот, меньше конечного значения параметра цикла при отрицательном шаге), переход к п. з), иначе к следующему пункту; д) выполняется тело цикла; е) параметр цикла автоматически увеличивается на значение шага; ж) переход к п. в); з) конец цикла.
Циклы с предусловием и постусловием в большинстве случаев (за исключением отдельных реализаций алгоритмических языков) являются более универсальными по сравнению с циклом с параметром, поскольку в последнем требуется заранее указать число повторений, в то время как в первых двух это не требуется. Цикл с параметром в любом случае может быть преобразован к циклу с пред- или постусловием. Обратное верно не всегда. Замечание. В языке C цикл for на самом деле является универсальным циклом с предусловием. В частности, из него можно сделать и описанную форму цикла с параметром. Примеры использования основных алгоритмических структур и их суперпозиций для составления алгоритмов, а по ним — программ приводятся в многочисленной литературе по программированию, поэтому не будем на них здесь останавливаться. Наконец, рассмотрим вопрос анализа алгоритмов. Одну и ту же задачу могут решать много алгоритмов. Эффективность работы каждого из них описывается разнообразными характеристиками. Прежде чем анализировать эффективность алгоритма, нужно доказать, что данный алгоритм правильно решает задачу. В противном случае вопрос об эффективности не имеет смысла. Если алгоритм решает поставленную задачу, то можно посмотреть, насколько это решение эффективно. При анализе алгоритма определяется количество “времени”, необходимое для его выполнения. Это не реальное число секунд или других промежутков времени, а приблизительное число операций, выполняемых алгоритмом. Число операций и измеряет относительное время выполнения алгоритма. Таким образом, иногда “временем” называют вычислительную сложность алгоритма. Фактическое количество секунд, требуемое для выполнения алгоритма на компьютере, непригодно для анализа, т.к. обычно интересует только относительная эффективность алгоритма, решающего конкретную задачу. Действительно, время, требуемое на решение задачи, — не очень хороший способ измерять эффективность алгоритма, потому что алгоритм не становится лучше, если его перенести на более быстрый компьютер, или хуже, если его исполнять на более медленном. На самом деле фактическое количество операций алгоритма на тех или иных входных данных не представляет большого интереса и не очень много сообщает об алгоритме. Реально определяется зависимость числа операций конкретного алгоритма от размера входных данных. Можно сравнить два алгоритма по скорости роста числа операций. Именно скорость роста играет ключевую роль, поскольку при небольшом размере входных данных алгоритм А может требовать меньшего количества операций, чем алгоритм В, но при росте объема входных данных ситуация может поменяться на противоположную. Два самых больших класса алгоритмов —
это алгоритмы с повторением и рекурсивные
алгоритмы. В основе алгоритмов с повторением
лежат циклы и условные выражения; для анализа
таких алгоритмов требуется оценить число
операций, выполняемых внутри цикла, и число
итераций цикла. Рекурсивные алгоритмы разбивают
большую задачу на фрагменты и применяются к
каждому фрагменту по отдельности. Такие
алгоритмы называются иногда “разделяй и
властвуй”, и их использование может оказаться
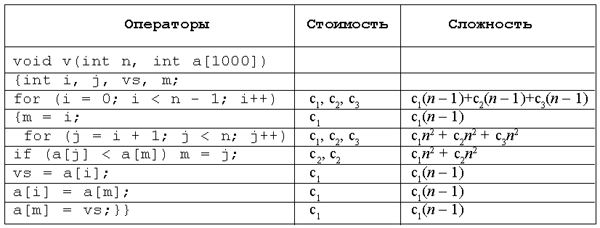
очень эффективным. Приведем пример оценки сложности алгоритма. Рассмотрим известный алгоритм сортировки выбором (здесь он записан в виде функции на C++) и оценим его сложность по описанной выше методике. void v(int n, int a[1000]) { int i, j, vs, m; for (i = 0; i < n - 1; i++) { m = i; for (j = i + 1; j < n; j++) if (a[j] < a[m]) m = j; vs = a[i]; a[i] = a[m]; a[m] = vs; } } Для каждой отдельной операции введем понятие “стоимости” (т.е. времени ее выполнения), в конечном итоге оценим, как зависит “время” выполнения алгоритма от размера сортируемого массива n. Суммируем S = c1(n – 1) + c2(n – 1) + c3(n – 1) + c1(n
– 1) + c1n2 + c2n2 + Таким образом, замечаем, что наибольший вклад в количество операций при больших n вносит величина n2, т.е. сложность алгоритма пропорциональна n2.
Использованные источники информации 1. Семакин И., Залогова Л.,
Русаков С., Шестакова Л. Информатика:
учебник по базовому курсу. М.: Лаборатория
Базовых Знаний, 1998. (Глава 12. Введение в 2. Угринович Н. Информатика и информационные технологии. Учебное пособие для общеобразовательных учреждений. М.: БИНОМ, 2001, 464 с. 3. Информатика. 7–8-е классы / Под ред. Н.В. Макаровой. СПб.: ПитерКом, 1999, 368 с. 4. Шафрин Ю.А. Информационные технологии. М.: Лаборатория Базовых Знаний, 1998, 704 с. (п. 1.6. Понятие об алгоритмах, п. 1.7. Понятие о программировании, с. 53–72). 5. Информатика. Задачник-практикум в 2 т. / Под ред. И.Г. Семакина, Е.К. Хеннера: Т. 1. М.: Лаборатория Базовых Знаний, 1999, 304 с. 6. Основы информатики и вычислительной техники. Пробное учебное пособие для средних учебных заведений / Под ред. А.П. Ершова, В.М. Монахова. М.: Просвещение, 1985. Ч. I, II. 7. Шауцукова Л.З. Информатика:
Учебник для 7. http://cjmp-science.narod.ru/didakt_i.html — дидактические и методические материалы по программированию и информатике. 8. Макконнелл Дж. Анализ алгоритмов. Вводный курс. М.: Техносфера, 2002, 304 с. 2. Средствами почтовой программы обеспечить автоматическое уведомление отправителя о получении от него письмаРассмотрим решение поставленной задачи в двух разных почтовых клиентах. Outlook Express В данной программе можно настроить получение уведомления о прочтении письма для каждого отправленного сообщения (настройка с помощью меню Сервис > Параметры > Уведомления).
Если уведомление требуется не часто, то эту настройку можно не осуществлять, а запросить уведомление непосредственно при создании сообщения.
Mail.ru При создании сообщения можно установить извещение о получении этого сообщения.
В других почтовых клиентах и бесплатных почтовых сервисах существует аналогичная возможность. 3. Подсчитать информационный объем графического файла по размеру в пикселях с учетом палитры (заданы количество цветов в палитре и размер рисунка) и того же рисунка в графическом формате со сжатием (задан коэффициент сжатия).Задан рисунок размером 1024х768 с представлением информации в формате RGB. Определить информационный объем графического файла, хранящего такой рисунок. Вычислить объем файла в том случае, если для хранения этого же рисунка используется формат со сжатием с коэффициентом 0,2. Решение В формате RGB для представления каждого пикселя используется три байта (по одному на каждый базовый цвет). Таким образом, получаем 1024 х 768 х 3 байта = 768 х 3 Кб = 2,25 Мб При использовании формата со сжатием получаем 2,25 Мб х 0,8 = 1,8 Мб |