ЭНЦИКЛОПЕДИЯ УЧИТЕЛЯ ИНФОРМАТИКИ

IV. Информационное моделирование

7. Моделирование экологических систем и процессов

Для изучения процессов, происходящих в экологических системах, используется как математическое, так и имитационное моделирование. В экологическом моделировании можно выделить два основных направления:

а) моделирование взаимодействия организмов друг с другом и с окружающей средой (“классическая” экология);

б) моделирование, связанное с состоянием окружающей среды и ее охраной (социальная экология).

Оба направления представлены большим количеством разработанных моделей.

 Классическая экология

В классической экологии рассматриваются взаимодействия нескольких типов:

· взаимодействие организма и окружающей среды;

· взаимодействие особей внутри популяции (популяция — это совокупность особей одного вида, существующих в одно и то же время и занимающих определенную территорию);

· взаимодействие между особями разных видов (между популяциями).

Математические модели в экологии используются практически с момента возникновения этой науки. И хотя поведение организмов в живой природе гораздо труднее адекватно описать средствами математики, чем самые сложные физические процессы, модели помогают установить некоторые закономерности и общие тенденции развития отдельных популяций, а также сообществ. Может показаться удивительным, что люди пытаются воссоздать живую природу в искусственной математической форме, но есть веские причины, которые стимулируют эти занятия. Вот некоторые цели создания математических моделей в классической экологии.

1. Модели помогают выделить суть или объединить и выразить с помощью нескольких параметров важные разрозненные свойства большого числа уникальных наблюдений, что облегчает экологу анализ рассматриваемого процесса или проблемы.

2. Модели выступают в качестве “общего языка”, с помощью которого может быть описано каждое уникальное явление; относительные свойства таких явлений становятся более понятными.

3. Модель может служить образцом “идеального объекта” или идеализированного поведения, при сравнении с которым можно оценивать и измерять реальные объекты и процессы.

При построении математических моделей в экологии используется опыт математического моделирования механических и физических систем, но с учетом специфических особенностей биологических систем:

· сложности внутреннего строения каждой особи;

· зависимости условий жизнедеятельности организмов от многих факторов внешней среды;

· незамкнутости экологических систем;

· огромного диапазона внешних характеристик, при которых сохраняется жизнеспособность систем.

Социальная экология

Моделирование, связанное с состоянием окружающей среды, в свою очередь, распадается на ряд направлений. Назовем некоторые из них:

· моделирование водных экосистем (трансформации компонент экосистемы, образования и превращения веществ, потребления, роста и гибели организмов);

· моделирование продукционного процесса растений (для выбора оптимальной стратегии проведения сельскохозяйственных мероприятий: орошения, полива, внесения удобрений, выбора сроков посева или посадки растений с целью получения максимального урожая);

· моделирование лесных сообществ (используются как для описания лесных массивов на больших пространственных и временных масштабах, так и для моделирования популяций, в которых основным объектом является отдельное дерево);

· моделирование загрязнения атмосферы и поверхности земли промышленными выбросами (перенос загрязняющих веществ, ущерб, наносимый здоровью населения, сельскохозяйственным угодьям, лесным массивам, почве, затраты на восстановление окружающей среды и т.д.);

· глобальные модели, в которых Земля рассматривается как единая экосистема. Наиболее известные модели такого рода — “ядерная зима” (катастрофические последствия ядерной войны), глобальное потепление (парниковый эффект вследствие промышленной деятельности человечества) и т.д.

Привлечение компьютеров существенно раздвинуло границы моделирования экологических процессов. С одной стороны, появилась возможность всесторонней реализации сложных математических моделей, не допускающих аналитического исследования, с другой — возникли принципиально новые направления (например, имитационное моделирование).

Методические рекомендации

Укажем на некоторые модели взаимодействия популяций, которые могут быть положены в основу изучения классических моделей экологии в рамках школьного курса информатики.

1. Динамика развития популяции с дискретным размножением с учетом внутривидовой конкуренции.

2. Динамика развития популяции с непрерывным размножением с учетом внутривидовой конкуренции. Логистическая модель.

3. Логистическая модель межвидовой конкуренции.

4. Моделирование системы “хищник–жертва”.

5. Имитационное моделирование динамики популяций.

Первая беседа по этой теме может быть посвящена введению в проблематику классической экологии и использованию в ней математических моделей. Следует дать определения таким понятиям, как “популяция”, “сообщество”, “внутривидовая конкуренция”, “межвидовая конкуренция”, сформулировать основные цели создания математических моделей в классической экологии.

После вводной лекции можно приступать к построению и исследованию конкретных моделей. Методически уместно начать с рассмотрения развития популяций с дискретным размножением, после чего следует плавный переход на популяции с непрерывным размножением. Естественная последовательность рассмотрения такова:

· динамическое моделирование численности изолированной популяции с дискретным размножением:

а) при отсутствии внутривидовой конкуренции;

б) при наличии внутривидовой конкуренции;

· динамическое моделирование численности изолированной популяции с непрерывным размножением:

а) при отсутствии внутривидовой конкуренции;

б) при наличии внутривидовой конкуренции;

· динамическое моделирование взаимодействия популяций:

а) состоящих в отношениях межвидовой конкуренции;

б) состоящих в отношениях “хищник–жертва”;

· имитационное моделирование развития популяции и взаимодействия популяций.

Обсудим методику построения и исследования моделей такого рода на нескольких примерах.

Пример 1. Моделирование развития изолированной популяции с дискретным размножением с учетом внутривидовой конкуренции.

Рассматриваются биологические виды, для которых потомки и предки не сосуществуют во времени (многочисленные растения, насекомые и др.). Тогда последовательные значения численности популяции можно представить N₀, N₁, ...

Если нет никаких причин ограничения численности популяции, тогда возникает простейшая очевидная модель: N_t+1 =  R · N_t, где R — коэффициент воспроизводства. Решение этой модели очевидно: N_t =  N₀ · R^t и при R > 1 численность популяции нарастает по геометрической прогрессии.

Даже эта простейшая модель заслуживает обсуждения. Она выражает то, что в литературе иногда называют “законом Мальтуса”.

Очевидно, что неограниченно долго возрастать популяция не может. Простейший способ учета внутривидовой конкуренции связан с гипотезой о том, что коэффициент воспроизводства не есть константа, а зависит от численности популяции, спадая по мере ее роста. На этом этапе следует разъяснить учащимся методику построения моделей в сфере знаний, где основным способом исследования являются наблюдения, в которой точные математические законы отсутствуют в силу сложности системы (в отличие от, например, физики). В такой ситуации делаются достаточно произвольные допущения, в значительной мере оправдываемые простотой, а полезность модели определяется путем сопоставления ее решений с закономерностями поведения реальных систем.

Проиллюстрируем это простым соображением. Итак, надо учесть, что величина R монотонно спадает с ростом величины N. Реального характера этого спада мы не знаем; его можно представить множеством способов с использованием общеизвестных элементарных функций, а если надо, то и выходом из этого класса.

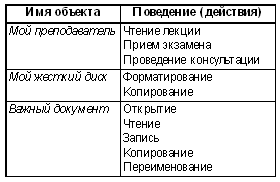
Модель, в основу которой положена простейшая из таких функций, выглядит следующим образом: Полезность модели следует из того, что описываемое ею поведение численности популяций многократно наблюдалось экологами в природе.

Далее ставим вопрос: достаточно ли этой модели для качественного описания развития любой популяции с дискретным размножением? Наблюдались ли качественно иные динамики развития таких популяций? Ответ должен быть положительным: в природе наблюдаются и существенно более сложные процессы, нежели монотонное возрастание численности популяции с выходом на стационар, предсказываемое описанной выше моделью. Поэтому продолжаем поиск более адекватных моделей.

В частности, целесообразно рассмотреть модель, предсказывающую четыре качественно разных типа динамики численности популяций (в зависимости от соотношения значений параметров): монотонное возрастание с выходом на стационар, колебательное установление численности, регулярное колебательное изменение (так называемые “предельные циклы”) и хаотическое поведение без каких-либо видимых закономерностей. Все эти типы динамик наблюдаются в природе.

Методика изучения сложных движений зависит от математической подготовки учащихся. Чаще всего предельные циклы и хаотическое поведение приводим описательно, иллюстративно, не стремясь дать определение этим сложным процессам. В классах же с высоким уровнем математической подготовки и выраженным интересом учащихся обсуждение этих вопросов может быть существенным элементом развития математических интересов.

При изучении моделей, выраженных дифференциальными уравнениями, методика исследования в основном остается та же. Она включает следующие этапы:

· постановку проблемы, введение терминологии, описание поведения соответствующих природных систем;

· построение математической модели;

· попытку качественного исследования модели, включая построение диаграмм на фазовой плоскости параметров модели;

· численное решение дифференциальных уравнений (как правило, простейшими из методов дискретизации, либо путем использования готовых программ).

Заметно иной является методика построения имитационных моделей экологических процессов.

Пример 2. Разработать имитационную модель системы “хищник–жертва” по следующей схеме.

“Остров” размером 20 ? 20 заселен дикими кроликами, волками и волчицами. Имеется по нескольку представителей каждого вида. Кролики в каждый момент времени с одинаковой вероятностью 1/9 передвигаются в один из восьми соседних квадратов (за исключением участков, ограниченных береговой линией) или просто сидят неподвижно. Каждый кролик с вероятностью 0,2 превращается в двух кроликов. Каждая волчица передвигается случайным образом, пока в одном из соседних восьми квадратов не окажется кролик, за которым она охотится. Если волчица и кролик оказываются в одном квадрате, волчица съедает кролика и получает одно очко. В противном случае она теряет 0,1 очка.

Волки и волчицы с нулевым количеством очков умирают.

В начальный момент времени все волки и волчицы имеют 1 очко.

Волк ведет себя подобно волчице до тех пор, пока в соседних квадратах не исчезнут все кролики; тогда, если волчица находится в одном из восьми близлежащих квадратов, волк гонится за ней.

Если волк и волчица окажутся в одном квадрате и там нет кролика, которого нужно съесть, они производят потомство случайного пола.

Задание: понаблюдать за изменением популяции в течение некоторого периода времени. Проследить, как сказываются на эволюции популяций изменения параметров модели.

Что же касается моделирования состояния окружающей среды, то оно почти всегда существенно сложнее, и в школьном курсе информатики представляется нецелесообразным заниматься реализацией таких моделей на уроках. Это не исключает возможности эксперимента с готовыми моделями подобного рода.

8. Объектно-информационные модели

Объектный подход к информационному моделированию берет свое начало в парадигме объектно-ориентированного программирования (ООП), возникшей в 1970-х годах (см. “Объектно-ориентированное программирование”). Главным понятием здесь является “объект”.

Объект — часть окружающей нас действительности.

Понятие объекта является очень широким и объединяет в себе как реальные, осязаемые предметы (например: кресло, автомобиль, мост), так и образы, созданные мышлением человека (например: стихотворение, музыкальное произведение, математическая теорема).

Информационная модель объекта должна отражать некоторый набор его свойств. Свойства объекта — это совокупность признаков, которые отличают его от других объектов. В следующей таблице даны примеры объектов и их свойств.

У каждого конкретного объекта свойства имеют определенные значения. В нашем примере добавим значения свойств объектов (см. таблицу на с. 5).

Эти значения могут быть количественными величинами (10 лет, 5 Гб), но могут быть и именами других объектов. Например, “Иван Иванович Иванов” и “Математика” сами могут рассматриваться как объекты.

Состояние объекта характеризуется перечнем всех возможных его свойств и текущими значениями каждого из этих свойств. Изменение состояния объекта отражается в его информационной модели изменением значений его свойств. Как правило, объекты не остаются неизменными. Например, растет стаж работы учителя И.И. Иванова; на жестком диске изменяется объем занятой памяти; документ может быть перенесен на другой диск, в другую папку и пр. Все эти процессы в информационной модели отражаются изменениями значений свойств.

В объектно-информационной модели отражаются не только свойства, но также и поведение объекта. Поведение объекта — действия, которые могут выполняться над объектом или которые может выполнять сам объект. Теперь опишем поведение объектов из нашего примера.

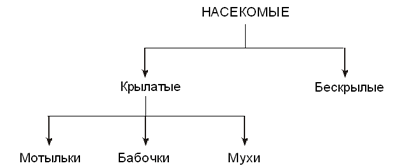
Объекты, обладающие одинаковыми свойствами и поведением, образуют класс объектов.

Каждый объект является экземпляром какого-либо класса. Все преподаватели обладают одним и тем же набором свойств (имя, стаж работы, читаемый курс) и поэтому образуют класс объектов. Присвоим этому классу имя “Преподаватель”. Каждый конкретный преподаватель — экземпляр этого класса (или объект). Следовательно, “Мой преподаватель” — экземпляр класса “Преподаватель”. Аналогично можно ввести класс “Жесткий диск”, объединив в нем все жесткие диски. Тогда “Мой жесткий диск” — экземпляр класса “Жесткий диск”. Если принять во внимание, что класс “Документ” описывает свойства и поведение всех документов, то “Важный документ” — экземпляр класса “Документ”.

Таким образом, экземпляр класса (объект) — это конкретный предмет или образ, а класс определяет множество объектов с одинаковыми свойствами и поведением. Класс может порождать произвольное число объектов, однако любой объект относится к строго фиксированному классу.

Иерархии классов. Объектно-информационные модели имеют иерархическую структуру (дерево). Иерархичность проявляется в том, что некоторый класс сам может быть подмножеством другого, более широкого класса. Вот пример иерархической классификации из биологии: вид “Насекомые” включает в себя два отряда: “Крылатые” и “Бескрылые”; в свою очередь, “Крылатые” насекомые делятся на подотряды: “Мотыльки”, “Бабочки”, “Мухи” и т.д.

В такой иерархической структуре между классами определяется отношение наследования.

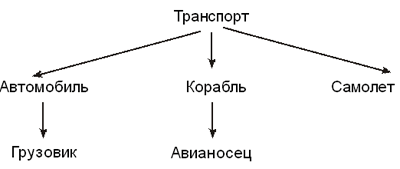
Фрагмент классификации насекомых

Наследование — это такое отношение между классами, когда один класс повторяет свойства и поведение другого класса.

Такой способ классификации, в частности, хорошо согласуется с механизмом биологического наследования в мире насекомых. Классы верхних уровней являются более общими по отношению к нижним. При спуске по дереву каждый следующий класс является более специфичным и в то же время наследует все свойства своих предшественников. Класс, свойства и поведение которого наследуются, называется суперклассом (или базовым классом). Производный от суперкласса класс называется подклассом. В нашем примере “Насекомые” — суперкласс для подклассов “Крылатые”, “Бескрылые”, “Мотыльки”, “Бабочки”, “Мухи”, а “Крылатые” — суперкласс для подклассов “Мотыльки”, “Бабочки”, “Мухи”. В подклассе дополняются свойства и уточняется поведение суперкласса. При определении класса “Мухи” нет необходимости вводить свойство “Наличие крыльев”, так как это свойство наследуется из суперкласса “Крылатые”.

Еще один пример. Рассмотрим систему классов, отражающих сведения о различных видах транспорта.

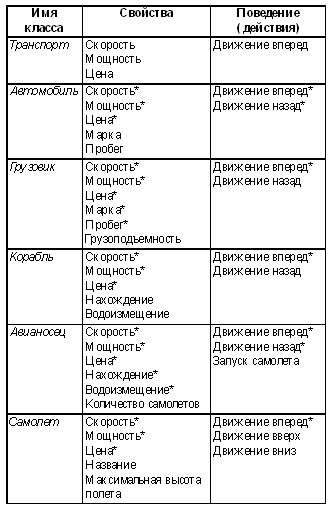
Свойства и поведение, присущие каждому классу, отражены в таблице ниже. Здесь звездочками отмечены наследуемые свойства и действия.

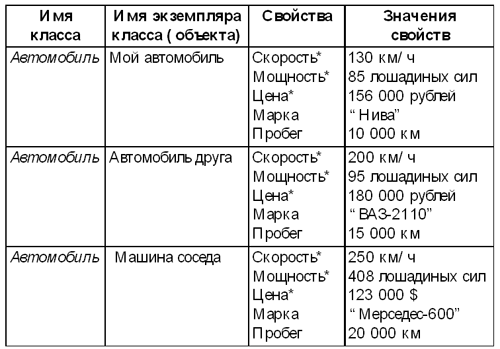
Все самые общие свойства располагаются в суперклассе “Транспорт”. Эти свойства наследуются классами “Автомобиль”, “Грузовик”, “Корабль”, “Авианосец” и “Самолет”. Кроме того, свойства “Марка” и “Пробег” наследуются классом “Грузовик” от базового класса “Автомобиль”, а свойства “Нахождение” и “Водоизмещение” наследуются классом “Авианосец” от базового класса “Корабль”. Столбец Поведение (действия) позволяет проследить наследование действий.

А теперь определим экземпляры классов (объекты) и значения их свойств.

Таким образом, определены три экземпляра класса “Автомобиль”. Для определения экземпляров (объектов) других классов необходимо аналогичным образом задать значения свойств.

Подводя итог, сделаем вывод о том, что такое объектно-информационная модель (ОИМ). ОИМ включает в себя описание иерархической системы классов, между которыми действуют отношения наследования. Для каждого класса определяется совокупность присущих ему свойств и действий (поведения), указывается, какие свойства и действия являются наследуемыми, а какие — специфическими. Для каждого объекта, входящего в ОИМ, указывается класс, элементом которого он является, а также конкретные значения свойств.

Методические рекомендации

Изучение объектного подхода к информационному моделированию имеет две дидактические задачи: во-первых, оно развивает системное мышление учащихся, во-вторых, имеет непосредственное отношение к современной методике программирования — объектно-ориентированному программированию.

Развитие системного мышления должно происходить путем анализа знакомых и понятных для учеников систем. Например: семья, школа, городской транспорт, учебные дисциплины и пр. Основной навык, который при этом формируется, заключается в умении выделить в этих системах отдельные объекты, перечислить некоторое множество их свойств и действий (поведения). Необходимо обратить внимание учеников на тот факт, что, как любая форма модели, объектно-информационная модель включает в себя лишь часть свойств объекта и его действий, существенных с позиции целей моделирования. Поэтому для построения объектно-информационной модели в первую очередь нужно договориться о целях моделирования.

Следующим важным моментом объектного моделирования является классификация объектов. Основное свойство определяемых классов — их иерархическая подчиненность. А связи между классами различных уровней иерархии реализуются через наследование свойств и поведения.

Освоение программирования на объектно-ориентированных языках (С++, Delphi и др.) в школе может происходить на уровне профильного обучения в старших классах. Его отличие от традиционного процедурного программирования заключается в способе мышления, сводящемся к умению выстраивать объектно-информационные модели (иерархии классов).

9. Системный анализ

Для того чтобы получить информационную модель любого реального объекта или процесса, необходимо рассмотреть его с системной точки зрения — выполнить системный анализ объекта. Задача системного анализа, который проводит исследователь, — упорядочить свои представления об изучаемом объекте для того, чтобы отразить их в информационной модели. Таким образом, просматривается следующий порядок этапов перехода от реального объекта к информационной модели:

Понятие системы

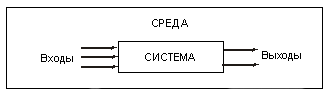
Под системой понимается любой объект, состоящий из множества взаимосвязанных частей и существующий как единое целое.

Наука о системах называется системологией. Любой объект окружающего мира можно рассматривать как систему. Системы бывают материальные, нематериальные и смешанные. Примеры материальных систем: дерево, здание, человек, планета Земля, Солнечная система. Примеры нематериальных систем: человеческий язык, математика. Пример смешанных систем — школа. Она включает в себя как материальные части (школьное здание, оборудование, тетради, учебники и пр.), так и нематериальные (учебные планы, программы, расписания уроков).

Все разнообразие существующих систем можно разделить на две категории: на естественные системы, т.е. существующие в природе, и искусственные системы — созданные человеком. Например, Солнечная система — естественная, а компьютер — искусственная система. Для всякой искусственной системы существует цель ее создания человеком: автомобиль — перевозить людей и грузы, компьютер — работать с информацией, завод — производить продукцию. В системологии искусственную систему определяют как “средство достижения цели”*. Именно целесообразностью системы определяется ее состав и структура.

Состав системы — это множество входящих в нее частей. В качестве примера системы рассмотрим объект, с которым ученикам приходится иметь дело на уроках информатики, — персональный компьютер.

Самое поверхностное описание ПК такое: это система, составными частями которой являются системный блок, клавиатура, монитор, принтер, мышь. Можно ли назвать их простыми элементами компьютера? Конечно, нет! Каждая из этих частей — это тоже система, состоящая из множества взаимосвязанных частей. В состав системного блока входят: центральный процессор, оперативная память, накопители на жестких и гибких магнитных дисках, CD-ROM, контроллеры внешних устройств и пр. В свою очередь, каждое из этих устройств — также сложная система. Например, центральный процессор состоит из арифметико-логического устройства, устройства управления, регистров. Так можно продолжать и дальше, все более углубляясь в подробности устройства компьютера.

Систему, входящую в состав какой-то другой, более крупной системы, называют подсистемой.

Из данного определения следует, что системный блок является подсистемой персонального компьютера, а процессор — подсистемой системного блока.

А можно ли сказать, что какая-то простейшая деталь компьютера, например гайка, системой не является? Все зависит от точки зрения. В устройстве компьютера гайка — простая деталь, поскольку на более мелкие части она не разбирается. Но с точки зрения строения вещества, из которого сделана гайка, это не так. Металл состоит из молекул, образующих кристаллическую структуру, молекулы — из атомов, атомы — из ядра и электронов. Чем глубже наука проникает в вещество, тем больше убеждается, что нет абсолютно простых объектов. Даже частицы атома, которые называли “элементарными” (например, электроны), тоже оказались не простыми.

Любой реальный объект бесконечно сложен. Описание его состава и структуры всегда носит модельный характер, т.е. является приближенным. Степень подробности такого описания зависит от его назначения. Одна и та же часть системы в одних случаях может рассматриваться как ее простой элемент, в других случаях — как подсистема, имеющая свой состав и структуру.

Структура системы

Всякая система определяется не только составом своих частей, но также порядком и способом объединения этих частей в единое целое. Все части (элементы) системы находятся в определенных отношениях или связях друг с другом. Здесь мы выходим на следующее важнейшее понятие системологии — понятие структуры.

Структура — это совокупность связей между элементами системы.

Можно еще сказать так: структура — это внутренняя организация системы. Многие открытия в науке связаны именно с выяснением структуры природных систем. Например, экспериментально было доказано, что атом состоит из положительно и отрицательно заряженных частиц. Однако лишь открытие орбитальной структуры атома, сделанное Нильсом Бором, в полной мере объяснило природу атома. Стали понятны многие физические явления (например, механизм электромагнитного излучения).

Всякая система обладает определенным составом и структурой. Свойства системы зависят от того и от другого. Даже при одинаковом составе системы с разной структурой обладают разными свойствами, могут иметь разное назначение.

С примерами зависимости свойств различных систем от их структуры ученики встречаются в разных школьных дисциплинах. Например, известно, что графит и алмаз состоят из молекул одного и того же химического вещества — углерода. Но в алмазе молекулы углерода образуют кристаллическую структуру, а у графита структура совсем другая — слоистая. В результате алмаз — самое твердое в природе вещество, а графит — мягкий, из него делают грифели для карандашей. В химии известно явление, которое называется изомерией. Вещества, состоящие из молекул одинакового атомарного состава, но различающиеся структурой молекул, обладают разными свойствами.

Типы связей в системах

Связи в системах бывают материальными и информационными. В естественных системах неживой природы (космические системы, атомы и молекулы, природные системы на Земле и пр.) связи носят только материальный характер, а в системах живой природы существуют связи материальные и информационные.

Информационные связи — это обмен информацией между частями системы, поддерживающий ее целостность и функциональность.

Очевидно существование информационных связей в животном мире, в человеческом обществе. В технических системах, используемых в информационной сфере (радио, телевидение, компьютерные сети), также действуют связи информационного типа. В них информация — это семантическое содержание физических сигналов, передаваемых между частями системы.

Общественные (социальные) системы — это различные объединения людей. Конечно, между ними тоже есть определенные материальные связи (например, общее помещение, экономическая зависимость, родственно-генетические связи), но очень важны информационные связи. Ни один коллектив, от семьи до государства, не может существовать без информационного обмена.

Системный эффект

Следующее важное положение системологии формулируется так: всякая система приобретает новые качества, не присущие ее составным частям.

Например, отдельные детали велосипеда: рама, руль, колеса, педали, сиденье — не обладают способностью к езде. Но вот эти детали соединили определенным образом, создав систему под названием “велосипед”, которая приобрела новое качество — способность к езде, т.е. возможность служить транспортным средством. Этим свойством не обладала ни одна из деталей в отдельности. То же самое можно показать на примере самолета: ни одна часть самолета в отдельности не обладает способностью летать; но собранный из них самолет (система) — летающее устройство. Еще пример: социальная система — строительная бригада. Один рабочий, владеющий одной специальностью (каменщик, сварщик, плотник, крановщик и пр.), не может построить многоэтажный дом, но вся бригада вместе справляется с этой работой.

Появление нового качества у системы называется системным эффектом. Это же свойство выражается фразой: “Целое больше суммы своих частей”.

Модели систем

Наши представления о реальных системах носят приближенный, модельный характер. Описывая в какой-либо форме реальную систему, мы создаем ее информационную модель. Рассмотрим три разновидности информационных моделей систем:

— модель “черного ящика”;

— модель состава;

— структурная модель.

Модель “черного ящика”. Всякая система — это нечто цельное и выделенное из окружающей среды. Система и среда взаимодействуют между собой. В системологии используются представления о входах и выходах системы. Вход системы — это воздействие на систему со стороны внешней среды, а выход — это воздействие, оказываемое системой на окружающую среду. Такое представление о системе называется моделью “черного ящика” (см. рисунок).

Модель “черного ящика”

Модель “черного ящика” используется в тех случаях, когда внутреннее устройство системы недоступно или не представляет интереса, но важно описать ее внешние взаимодействия. Например, в любой инструкции по использованию бытовой техники (телевизор, магнитофон, стиральная машина и пр.) дается описание работы с ней на уровне входов и выходов: как включить, как регулировать работу, что получим на выходе. Такого представления может быть вполне достаточно для пользователя данной техникой, но не достаточно для специалиста по ее ремонту.

Модель “черного ящика” отражает лишь взаимодействие системы с окружающей средой. Такой подход к сложным системам был введен в кибернетике. Казалось бы, это простейшая модель, которая не углубляется во внутреннее устройство системы. Однако и внешние взаимодействия реальной системы оказываются бесконечно сложными. Поэтому модель “черного ящика”, как и любая другая, строится в соответствии с целью моделирования, учитывая лишь те входы и выходы системы, которые существенны с точки зрения цели моделирования, назначения создаваемой модели.

Если описать компьютер как “черный ящик”, учитывая только его информационное взаимодействие с внешней средой, то модель получится следующей:

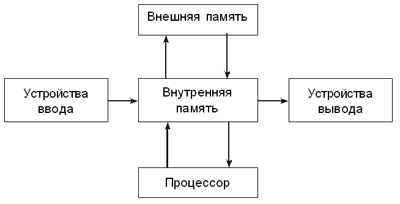
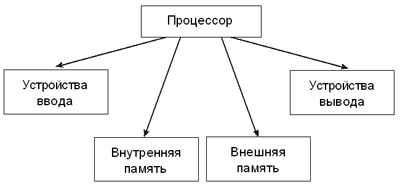
Модель “черного ящика” компьютера

Если, кроме информационного, учитывать еще и физическое взаимодействие компьютера с внешней средой, то на входе надо добавить: “электропитание”, “температурное воздействие”, “вибрационное воздействие”. На выходе: “излучение экрана”, “шум вентилятора”, “нагрев от монитора”. В таком расширенном списке входов и выходов следует выделить основные параметры и побочные. Основные — это те, которые связаны с главной функцией системы: работа с информацией. Среди побочных можно выделить необходимые (электропитание) и нежелательные (излучение экрана, шум вентилятора).

Модель можно расширить, добавив в нее экономические параметры, связанные с финансовыми расходами на входе (исходная цена, оплата электроэнергии, оплата за пользование Интернетом) и возможными доходами на выходе, если компьютер является рабочим инструментом, в результате использования которого человек зарабатывает деньги.

Модель состава системы дает описание входящих в нее элементов и подсистем, но не рассматривает связей между ними. Очевидно, что и модель состава компьютера может иметь разные варианты в зависимости от отражаемой в ней точки зрения на систему. Например:

Вариант 1: системный блок, клавиатура, монитор, принтер, мышь.

Вариант 2: оперативная память, внешняя память, центральный процессор, устройства ввода, устройства вывода.

Вариант 3: центральный процессор, ОЗУ, ПЗУ, жесткий диск, флоппи-диск, лазерный диск, информационная магистраль, клавиатура, монитор, контроллеры внешних устройств и пр.

Структурную модель системы еще называют структурной схемой. На структурной схеме отражается состав системы и ее внутренние связи. Наряду с термином “связь” нередко употребляют термин “отношение”.

Наглядным способом описания структурной модели системы являются графы (см. “Графические модели”). На рисунке в виде ориентированного графа приведена структурная модель компьютера.

Структурная модель кмпьютера с информационными связями

Здесь стрелки обозначают информационные связи между элементами системы. Направление стрелок указывает на направление передачи информации.

Однако если нас интересуют связи по управлению, то получится следующая граф-модель компьютера:

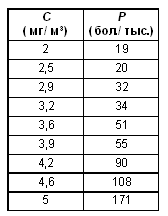
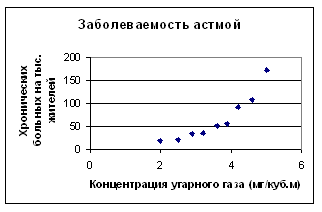
Структурная модель кмпьютера со связями по управлению

Здесь стрелка обозначает направление управляющего воздействия. Смысл схемы заключается в том, что процессор управляет работой всех остальных устройств компьютера.

Следовательно, структурная модель одной и той же системы может быть разной. Все определяется целями моделирования.

Методические рекомендации

Одной из наиболее заметных тенденций в современном развитии школьной информатики стало проникновение в ее содержание элементов системного анализа. Знакомство учащихся с системным анализом может происходить по двум целевым направлениям:

— развитие системного мышления учащихся;

— знакомство с системным анализом как этапом информационного моделирования.

Начиная обсуждение понятия “система”, следует обратить внимание учащихся на то, что с этим понятием они многократно встречались как в учебных дисциплинах, так и в повседневной жизни. Примеров можно привести достаточно много: Солнечная система, периодическая система химических элементов, системы растений и животных, система образования, система транспорта, система здравоохранения и многое другое. Безусловно, ученики имеют некоторое интуитивное понимание того, что такое система. Однако для информатики это понятие является одним из фундаментальных и поэтому здесь нельзя ограничиться интуитивным представлением.

Сформулировав определение системы, его необходимо подробно обсудить. В ходе такого обсуждения следует использовать знакомые и понятные ученикам примеры систем. Наряду с теми, что были перечислены выше, нужно напомнить примеры систем, с которыми ученики встречались в курсе информатики. Например, совокупность взаимосвязанных данных, предназначенных для обработки на компьютере, называется системой данных. Совокупность взаимосвязанных программ определенного назначения образует программные системы: операционные системы, системы программирования. Файловая система — организованная совокупность файлов и папок на дисках компьютера.

Двигаясь от интуитивного представления учащихся о системах к более строгому, научному пониманию, необходимо последовательно раскрыть следующие свойства систем:

— функция (цель, назначение) системы;

— взаимодействие системы с окружающей средой;

— состав системы;

— структура системы;

— системный эффект.

На конкретных примерах необходимо показать неразрывность системного анализа с информационным моделированием. Информационная модель базируется на данных, т.е. на информации об объекте моделирования. Любой реальный объект — это сложная система, которая обладает бесконечным множеством различных свойств и характеристик. Важнейшим этапом моделирования является разделение параметров, характеризующих моделируемый объект или процесс, по степени важности влияния их изменений на поведение объекта или процесса, — то поведение, которое представляется важным с точки зрения достижения целей моделирования. Такой процесс называется ранжированием. Чаще всего невозможно (да и не нужно) учитывать все факторы, которые могут повлиять на поведение объекта или процесса, — нужно выделить важнейшие из них. От того, насколько удачно на этапе системного анализа будут выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективность достижения цели.

Выделить более важные (или, как говорят, значимые) факторы и отсеять менее важные может лишь специалист в той предметной области, к которой относится модель. Например, если учитель хочет создать модель учебного процесса в классе, то ему потребуются данные об изучаемых предметах, расписании занятий, сведения об оценках учеников, о преподавателях. Если же он задался целью смоделировать процесс летнего отдыха (например, коллективную поездку на юг), то ему потребуются совсем другие данные: сроки поездки, маршрут поезда, стоимость билетов, стоимость расходов на питание и пр. Возможно, что единственными общими данными для этих двух моделей будет список учеников класса.

Статистика — наука о сборе, измерении и анализе массовых количественных данных. Существуют медицинская статистика, экономическая статистика, социальная статистика и другие.

Рассмотрим пример из области медицинской статистики. Врачам известно, что наиболее сильное влияние на бронхиально-легочные заболевания людей оказывает угарный газ — оксид углерода. Поставив цель определить эту зависимость, специалисты по медицинской статистике проводят сбор данных. Они собирают сведения из разных городов о средней концентрации угарного газа в атмосфере и о заболеваемости астмой (число хронических больных на 1000 жителей). Полученные данные можно свести в таблицу, а также представить в виде точечной диаграммы.

Статистические данные в табличном
и дискретно-графическом виде

Проанализировав результаты, можно сделать вывод, что при концентрации угарного газа до 3 мг/м3 его влияние на заболеваемость астмой несильное.
С дальнейшим ростом концентрации наступает резкий рост заболеваемости.

Статистические данные всегда являются приближенными, усредненными; они носят оценочный характер, но верно отражают характер зависимости величин. И еще одно важное замечание: для достоверности выводов, полученных путем статистического анализа, данных должно быть много.

Регрессионные статистические модели

Математической моделью рассмотренного явления может быть функция, отражающая зависимость числа хронических больных Р от концентрации угарного газа С. Вид этой функции неизвестен, ее следует искать методом подбора по экспериментальным данным.

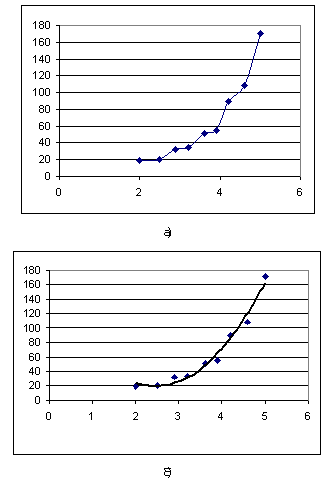
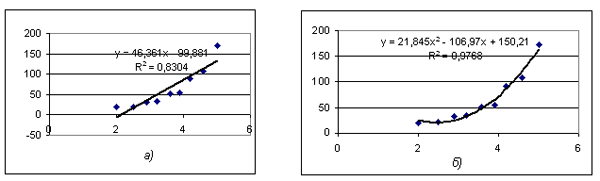
Графики зависимостей

График искомой функции должен проходить близко к точкам диаграммы экспериментальных данных. Строить функцию так, чтобы ее график точно проходил через все данные точки (рисунок а), не имеет смысла, поскольку экспериментальные значения являются приближенными. Отсюда следуют основные требования к искомой функции:

— график этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны (рисунок б);

— среди возможных в этом плане функций желательно отыскать достаточно простую (для использования ее в дальнейших вычислениях).

Такую функцию принято называть в статистике регрессионной моделью.

Построение регрессионной модели происходит в два этапа:

1) подбор вида функции;

2) вычисление параметров функции.

Первая задача не имеет строгого решения. Здесь могут помочь опыт и интуиция исследователя, а возможен и “слепой” перебор из конечного числа функций и выбор лучшей из них. Например, это может быть линейная функция y = ax + b, квадратичная y = ax² + bx + c или более сложная.

Если пробная функция выбрана, то следующим шагом нужно подобрать параметры (a, b, c и пр.) так, чтобы функция располагалась как можно ближе к экспериментальным точкам. Классический способ подбора параметров называется методом наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квадратов отклонений у-координат всех экспериментальных точек от у-координат графика функции была бы минимальной.

На рисунке изображены две функции, построенные методом наименьших квадратов (с помощью MS Excel) по данным, представленным в приведенной выше таблице. Значение R² позволяет оценить качество приближения: чем оно меньше, тем приближение лучше. Таким образом, можно сделать вывод: квадратичная функция дает лучшее регрессионное приближение, чем линейная. Разумеется, отсюда не следует, что не существует лучшей зависимости. Возможен дальнейший поиск с опорой на качественные соображения и опыт исследователя.

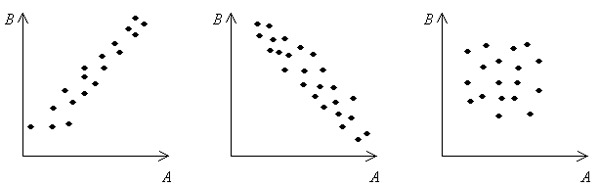
Линейная и квадратичная зависимости. построенные с помощью МНК (линии тренда)

Регрессионные модели, как правило, используются с целью прогноза поведения системы. Определение зависимой величины Y для промежуточных значений аргумента Х называется интерполяцией. Продолжение линии тренда за границы области данных, приведенных в исходной таблице, называется экстраполяцией. Однако не следует слишком далеко удаляться от области экспериментальных данных, поскольку нет гарантии, что там характер зависимости не изменится.

Моделирование корреляционных связей

Функциональная зависимость между двумя величинами является в некотором смысле самой простой из возможных зависимостей. Если величина y является функцией от величины x, то значение x полностью и однозначно определяет значение y.

Однако бывают (и в реальной жизни гораздо чаще) случаи, когда зависимость, несомненно, есть, но она не имеет однозначного выражения. Простой вопрос: определяет ли рост человека его вес, т.е. можно ли сказать, что при росте 170 см вес обязательно равен некоторому определенному значению? Конечно, нет. На вес человека накладывают отпечаток многие факторы. Но правильно ли на основании этого утверждать, что вес от роста не зависит? Тоже нет. На бытовом уровне ответ таков: вообще говоря, чем больше рост, тем больше вес. “Вообще говоря” здесь означает, что точной (функциональной) зависимости нет, но есть некоторая иная, а именно корреляционная, зависимость.

Корреляция — систематическая и обусловленная связь между двумя рядами данных. Например, ростом и весом; датой и дневной температурой, числом компьютеров в классе и средней оценкой в этом классе на ЕГЭ по информатике и т.п. Можно сказать иначе: корреляция — это связь переменных, при которой одному значению одного признака соответствует несколько значений другого признака, отклоняющегося в ту или иную сторону от своего среднего значения.

Подобные ситуации проиллюстрированы на рисунке, представляющем экспериментально измеренные данные парных значений двух величин, А и В. “Облако точек” на каждом из них соответствует трем разным ситуациям: первые два “облака” похожи на линейную зависимость (в одном случае возрастание значения А сопровождается возрастанием В, во втором — убыванием значения В); в третьем случае никакой зависимости не просматривается. О первой ситуации говорят, что имеет место сильная положительная линейная корреляция, второй — сильная отрицательная корреляция; в третьем случае корреляция отсутствует.

Множественные зависимости величин А и В

Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными зависимостями. Раздел математической статистики, который исследует такие зависимости, называется корреляционным анализом. Корреляционный анализ изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости.

Формальная постановка задачи корреляционного анализа выглядит так: пусть важной характеристикой некоторой сложной системы является фактор А. На него могут оказывать влияние одновременно многие другие факторы: B, C, D и т.д. Для исследователя могут представлять интерес два типа задач:

1) Оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А?

2) Какие из факторов — B, C, D и т.д. — оказывают наибольшее влияние на фактор А?

Оценку корреляции величин начинают с высказывания гипотезы о возможном характере зависимости между их значениями. Простейшее допущение — наличие линейной зависимости. В таком случае мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции.

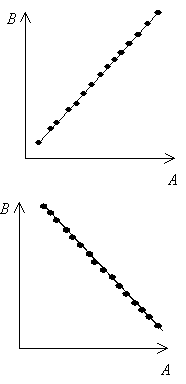
Коэффициент корреляции (обычно обозначаемый греческой буквой ) есть число, заключенное в диапазоне от –1 до +1;

· если это число по модулю близко к 1, то имеет место сильная корреляция, если к 0, то слабая;

· близость к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, к –1 означает обратное.

В случае полной положительной корреляции этот коэффициент равен (+1), а при полной отрицательной — (–1). На графике “облако точек” в этих случаях уже не “облако”: точки точно ложатся на прямые, как это отображено на рисунке.

Сильные корреляции

Если же точки не выстраиваются по прямой линии, а образуют “облако”, коэффициент корреляции по абсолютной величине становится меньше единицы и, по мере округления этого облака, приближается к нулю, то между переменными точно нет линейной корреляционной зависимости.

На практике пользуются понятиями “сильная корреляция” и “слабая корреляция”. Это достаточно условные понятия. В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Следует, однако, иметь в виду, что все это годится лишь при большом количестве точек, по которым вычисляется коэффициент корреляции. Говоря более формально, важен не только сам коэффициент, но и степень его достоверности, для вычисления которой существуют специальные правила.

Для вычисления коэффициента корреляции используется формула:

,

— где — сумма произведений данных из каждой пары;

n — число пар;

— средняя для данных переменной А;

— средняя для данных переменной В;

s_А — стандартное отклонение для распределения А;

s_В — стандартное отклонение для распределения В.

Коэффициент корреляции определяет степень, с которой значения двух переменных “пропорциональны” друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость.

Методические рекомендации

Построение и исследование несложных статистических моделей уместно в рамках изучения темы “Информационное моделирование” в 11-м классе. Оно может послужить как математическому образованию учащихся, так и освоению компьютерных технологий, применяемых для статистического моделирования.

Поскольку элементы математической статистики далеко не всегда изучаются в школьном курсе математики, учителю следует сделать введение в математическую постановку проблемы. При изучении построения регрессионных моделей возможны два подхода:

1) изложить детально метод наименьших квадратов;

2) обойти этот этап, перейдя сразу к технологии построения регрессионных зависимостей на базе одного из пакетов прикладных математических программ; простейший вариант — программа Excel.

В качестве примера опишем способ получения с помощью MS Excel регрессионной модели по методу наименьших квадратов для приведенной выше задачи медицинской статистики. Начать надо с ввода табличных данных и построения точечной диаграммы. Далее следует:

щелкнуть мышью по полю диаграммы;

выполнить команду Диаграмма Добавить линию тренда;

в открывшемся окне на закладке “Тип” выбрать “Линейный тренд”;

перейти к закладке “Параметры”; установить галочки на флажках “показывать уравнения на диаграмме” и “поместить на диаграмму величину достоверности аппроксимации R^2”, щелкнуть по кнопке OK.

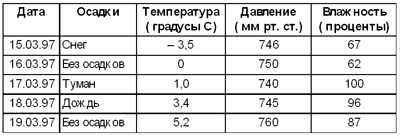
Диаграмма готова! Аналогично можно получить и другие типы трендов. Квадратичный тренд получается путем выбора полиномиального типа функции с указанием степени 2.

Заметим, что MS Excel дает возможность пользователю самому задавать тип регрессионной модели, а не ограничиваться предлагаемым меню из шести функций. Однако для большого числа практических ситуаций этих функций бывает вполне достаточно.

11. Табличные модели

Представление информации в табличной форме широко распространено. Уже в школьной жизни приходится встречаться с массой таблиц: расписание занятий, журнал успеваемости, график дежурств, таблица Менделеева, таблицы физических свойств веществ, таблицы исторических дат и многое другое. Информация в таблицах обязательно упорядочена по какому-то принципу. Например, в классном журнале — в алфавитном порядке фамилий учеников; в расписании занятий — по дням недели и номерам уроков и т.д. Такая упорядоченность позволяет быстро находить в таблице нужные сведения.

Чаще всего используются прямоугольные таблицы, состоящие из строк и столбцов (граф). В верхней строке таблицы обычно располагаются заголовки граф. Вот пример прямоугольной таблицы, содержащей сведения о погоде в течение нескольких дней.

Погода

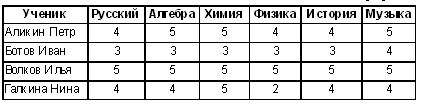
Данная таблица является примером таблицы типа “объект-свойство”. Каждая строка такой таблицы относится к конкретному объекту. В нашем примере это определенный день, заданный датой. Первая графа обычно идентифицирует этот объект, последующие графы отражают свойства (характеристики) объекта.

Другой тип таблиц называется “объект-объект”. Такие таблицы отражают взаимосвязь между различными объектами. Примером является таблица успеваемости учеников по разным предметам.

Успеваемость

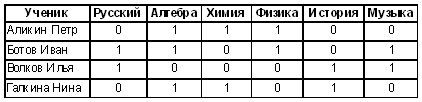
Эта таблица отражает связь между двумя типами объектов: учениками и изучаемыми дисциплинами. Оценка является характеристикой такой связи. В такой таблице строки и графы могут поменяться местами: в строках — предметы, в столбцах — ученики.

Важной разновидностью таблиц типа “объект-объект” являются двоичные матрицы. Двоичные матрицы отображают качественную связь между объектами — есть связь или нет связи. Например, если бы ученики могли выбирать изучаемые предметы по своему усмотрению, то сведения о том, кто что изучает, можно было бы представить в виде следующей таблицы (в ней единица указывает на изучаемый предмет, а ноль — на не изучаемый).

Изучаемые предметы

Табличный способ представления данных является универсальным. Любую структуру данных, в том числе и представленную в форме графа, можно свести к табличной форме. Приведение информации к табличной форме называется нормализацией данных. В следующей таблице представлен результат нормализации иерархической структуры, приведенной в статье “Графические модели” 2.

Заполнение этой таблицы происходило путем движения по дереву снизу вверх (от листьев к корню). Получилась таблица типа “объект-свойство”.

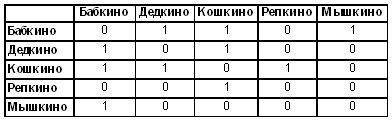
Объекты — города, а свойствами является их принадлежность к соответствующим административно-географическим зонам. Строки упорядочены в алфавитной последовательности названий городов. Число граф в таблице равно числу уровней в дереве. Нет смысла заводить графу под названием “Государство”, поскольку во всех строчках в ней будет присутствовать одно значение — “Российская Федерация”. Лучше это слово вынести в заголовок таблицы.

Для табличного представления сетей, содержащих однотипные вершины, используют двоичные матрицы. В следующей таблице содержится двоичная матрица, представляющая структуру дорожной сети, приведенной в статье “Графические модели”2.

Дорожная сеть

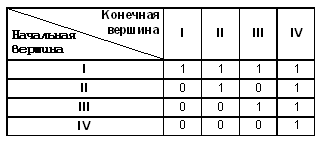
Двоичная матрица в этой таблице называется матрицей смежности: единицы стоят на пересечении строки и столбца с названиями смежных (т.е. соединенных дорогой) поселков. Если сеть является неориентированным графом, то матрица смежности симметрична относительно главной диагонали, идущей от верхнего левого угла в правый нижний угол матрицы. Вследствие этого, если строки и столбцы поменять местами, то матрица не изменится.

У матрицы, отражающей ориентированный граф, такой симметричности не будет. В этом случае надо договориться о смысле строк и столбцов. Например, для каждой пары смежных вершин строка обозначает начальную, а столбец — конечную вершину. Тогда структура ориентированного графа совместимостей групп крови из статьи “Графические модели” 2 представится следующей двоичной матрицей смежности:

Основанием для перевода графов в табличную форму служит то обстоятельство, что табличная форма удобна для компьютерной обработки. Многие компьютерные технологии работают с таблицами (базы данных, электронные таблицы); обработку таблиц удобно описывать на языках программирования. Поэтому представление систем в форме графа обычно используется в теоретических моделях; в компьютерном моделировании таких систем обычно используется табличная форма.

Методические рекомендации

Умение представлять данные в табличной форме — очень полезный общеметодический навык. Практически все школьные предметы используют таблицы, но никакой из них не учит школьников методике построения таблиц. Эту задачу должна взять на себя информатика. Приведение данных к табличной форме является одним из приемов систематизации информации — типовой задачи информатики.

Среди разделов базового курса, относящихся к линии информационных технологий, непосредственное отношение к таблицам имеют базы данных и электронные таблицы. Предварительный разговор о таблицах, их классификации, приемах оформления является полезной пропедевтикой к изучению этих технологий.

Возможная в школьном курсе информатики классификация таблиц описана выше: таблицы типа “объект-свойство” и “объект-объект”. Это наиболее простые и наиболее часто встречающиеся типы таблиц. Кроме них, полезно дать представление о двоичных матрицах. Двоичные матрицы используются в тех случаях, когда нужно отразить наличие или отсутствие связей между отдельными элементами некоторой системы. С помощью двоичных матриц удобно представлять сетевые структуры.

Пример. Дана двоичная матрица, отражающая связи между различными серверами компьютерной сети.

Глядя на таблицу, ученики должны определить, какой из пяти серверов является узловым.

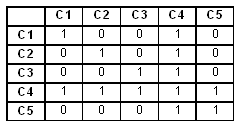
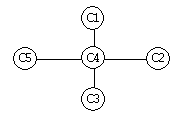
Решение следующее: поскольку по данному определению узловым называется тот сервер, с которым непосредственно связаны все другие серверы, то в матрице нужно искать строку, состоящую только из единиц. Это строка С4. Значит, сервер С4 является узловым.

Второе задание, связанное с этой же таблицей, может быть следующим: нарисовать схему компьютерной сети, изобразив серверы кружками, а связи между ними линиями. Вот решение этой задачи:

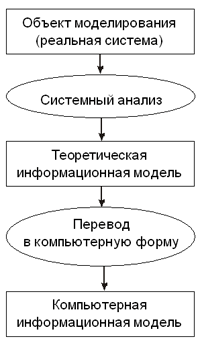
Этот пример еще раз демонстрирует, что для зрительного восприятия структуры системы удобнее графическая форма, а для компьютерной обработки — табличная.

Модель — это искусственно создаваемый объект, заменяющий некоторый объект реального мира (объект моделирования) и воспроизводящий ограниченное число его свойств. Понятие модели относится к фундаментальным общенаучным понятиям, а моделирование — это метод познания действительности, используемый различными науками.

Объект моделирования — широкое понятие, включающее объекты живой или неживой природы, процессы и явления действительности. Сама модель может представлять собой либо физический, либо идеальный объект. Первые называются натурными моделями, вторые — информационными моделями. Например, макет здания — это натурная модель здания, а чертеж того же здания — это его информационная модель, представленная в графической форме (графическая модель).

В экспериментальных научных исследованиях используются натурные модели, которые позволяют изучать закономерности исследуемого явления или процесса. Например, в аэродинамической трубе моделируется процесс полета самолета путем обдувания макета самолета воздушным потоком. При этом определяются, например, нагрузки на корпус самолета, которые будут иметь место в реальном полете.

Информационные модели используются при теоретических исследованиях объектов моделирования. В наше время основным инструментом информационного моделирования является компьютерная техника и информационные технологии.

Компьютерное моделирование включает в себя процесс реализации информационной модели на компьютере и исследование с помощью этой модели объекта моделирования — проведение вычислительного эксперимента.

Формализация

К предметной области информатики относятся средства и методы компьютерного моделирования. Компьютерная модель может быть создана только на основе хорошо формализованной информационной модели. Что же такое формализация?

Формализация информации о некотором объекте — это ее отражение в определенной форме. Можно еще сказать так: формализация — это сведеRние содержания к форме. Формулы, описывающие физические процессы, — это формализация этих процессов. Радиосхема электронного устройства — это формализация функционирования этого устройства. Ноты, записанные на нотном листе, — это формализация музыки и т.п.

Формализованная информационная модель — это определенные совокупности знаков (символов), которые существуют отдельно от объекта моделирования, могут подвергаться передаче и обработке. Реализация информационной модели на компьютере сводится к ее формализации в форматы данных, с которыми “умеет” работать компьютер.

Но можно говорить и о другой стороне формализации применительно к компьютеру. Программа на определенном языке программирования есть формализованное представление процесса обработки данных. Это не противоречит приведенному выше определению формализованной информационной модели как совокупности знаков, поскольку машинная программа имеет знаковое представление. Компьютерная программа — это модель деятельности человека по обработке информации, сведенная к последовательности элементарных операций, которые умеет выполнять процессор ЭВМ. Поэтому программирование на ЭВМ есть формализация процесса обработки информации. А компьютер выступает в качестве формального исполнителя программы.

Этапы информационного моделирования

Построение информационной модели начинается с системного анализа объекта моделирования (см. “Системный анализ”). Представим себе быстро растущую фирму, руководство которой столкнулось с проблемой снижения эффективности работы фирмы по мере ее роста (что является обычной ситуацией) и решило упорядочить управленческую деятельность. Первое, что необходимо сделать на этом пути, — провести системный анализ деятельности фирмы. Системный аналитик, приглашенный в фирму, должен изучить ее деятельность, выделить участников процесса управления и их деловые взаимоотношения, т.е. объект моделирования анализируется как система. Результаты такого анализа формализуются: представляются в виде таблиц, графов, формул, уравнений, неравенств и пр. Совокупность таких описаний есть теоретическая модель системы.

Следующий этап формализации — теоретическая модель переводится в формат компьютерных данных и программ. Для этого используется либо готовое программное обеспечение, либо привлекаются программисты для его разработки. В конечном итоге получается компьютерная информационная модель, которая будет использоваться по своему назначению.

Для примера с фирмой с помощью компьютерной модели может быть найден оптимальный вариант управления, при котором будет достигнута наивысшая эффективность работы фирмы согласно заложенному в модель критерию (например, получение максимума прибыли на единицу вложенных средств).

Классификация информационных моделей может основываться на разных принципах. Если классифицировать их по доминирующей в процессе моделирования технологии, то можно выделить математические модели, графические модели, имитационные модели, табличные модели, статистические модели
и пр. Если же положить в основу классификации предметную область, то можно выделить модели физических систем и процессов, модели экологических (биологических) систем и процессов, модели процессов оптимального экономического планирования, модели учебной деятельности, модели знаний и др. Вопросы классификации важны для науки, т.к. они позволяют сформировать системный взгляд на проблему, но преувеличивать их значение не следует. Разные подходы к классификации моделей могут быть в равной мере полезны. Кроме того, конкретную модель отнюдь не всегда можно отнести к одному классу, даже если ограничиться приведенным выше списком.

Методические рекомендации

Государственный образовательный стандарт предусматривает изучение вопросов, относящихся к информационному моделированию, как в базовом курсе основной школы, так и в старших классах. Примерная программа курса информатики рекомендует изучение темы “Формализация и моделирование” в
8-м классе на уровне примеров моделирования объектов и процессов. Прежде всего предполагается использование графических и табличных моделей.
В старших классах предусмотрено общее (теоретическое) введение в тему и изучение различных видов компьютерного моделирования на уровне математических (“расчетных”), графических, имитационных моделей, связанных с социальными, биологическими и техническими системами и процессами. Эффективной формой углубленного изучения компьютерного моделирования являются элективные курсы для старшеклассников.

Образовательные задачи, решаемые в ходе изучения информационного моделирования

Решение указанных ниже задач позволяет оказать существенное влияние на общее развитие и формирование мировоззрения учащихся, интегрировать знания по различным дисциплинам, осуществлять работу с компьютерными программами на более профессиональном уровне.

Общее развитие и становление мировоззрения учащихся

Курсы, ориентированные на моделирование, должны выполнять развивающую функцию, поскольку при их изучении учащиеся продолжают знакомство еще с одним методом познания окружающей действительности — методом компьютерного моделирования. В ходе работы с компьютерными моделями приобретаются новые знания, умения, навыки. Некоторые ранее полученные сведения конкретизируются и систематизируются, рассматриваются под другим углом зрения.

Овладение моделированием как методом познания

Основной упор в каждом из таких курсов необходимо сделать на выработку общего методологического подхода к построению компьютерных моделей и работе с ними. Необходимо

· продемонстрировать, что моделирование в любой области знаний имеет схожие черты; зачастую для различных процессов удается получить очень близкие модели;

· выделить преимущества и недостатки компьютерного эксперимента по сравнению с экспериментом натурным;

· показать, что и абстрактная модель, и компьютер представляют возможность познавать окружающий мир, а иногда и управлять им в интересах человека.

Выработка практических навыков компьютерного моделирования

На примере ряда моделей из различных областей науки и практической деятельности необходимо проследить все этапы компьютерного моделирования с исследования моделируемой предметной области и постановки задачи до интерпретации результатов, полученных в ходе компьютерного эксперимента, показать важность и необходимость каждого звена. При решении конкретных задач следует выделять и подчеркивать соответствующие этапы работы с моделью. Решение данной задачи предполагает поэтапное формирование практических навыков моделирования, для чего служат учебные задания с постепенно возрастающим уровнем сложности и компьютерные лабораторные работы.

Содействие профессиональной ориентации учащихся

Учащиеся старшей ступени школы стоят перед проблемой выбора будущей профессии. Проведение курса компьютерного моделирования способно выявить тех из них, кто имеет способности и склонность к исследовательской деятельности. Способности учащихся к проведению исследований следует развивать различными способами, на протяжении всего курса поддерживать интерес к выполнению компьютерных экспериментов с различными моделями, предлагать для выполнения задания повышенной сложности. Таким образом, развитие творческого потенциала учащихся и профориентация — одна из задач курса.

Преодоление предметной разобщенности, интеграции знаний

В рамках учебного курса целесообразно рассматривать модели из различных областей науки, что делает курс частично интегрированным. Для того чтобы понять суть изучаемого явления, правильно интерпретировать полученные результаты, необходимо не только владеть приемами моделирования, но и ориентироваться в той области знаний, где проводится модельное исследование. Реализация межпредметных связей в таком курсе не только декларируется, как это иногда бывает в других дисциплинах, но является зачастую основой для освоения учебного материала.

Развитие и профессионализация навыков работы с компьютером

Перед учащимися ставится задача не только реализовать на компьютере предложенную модель, но и наиболее наглядно, в доступной форме отобразить полученные результаты. Здесь может помочь построение графиков, диаграмм, динамических объектов, пригодятся и элементы мультипликации. Программа должна обладать адекватным интерфейсом, вести диалог с пользователем. Все это предполагает дополнительные требования к знаниям и умениям в области алгоритмизации и программирования, приобщает к более полному изучению возможностей современных парадигм и систем программирования.

Продолжение

* Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. М.: Высшая школа, 1989
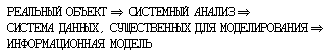
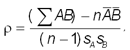