Курсы повышения квалификации
Математические основы информатики
А.Г. Гейн
Учебный план
| №_ГАЗЕТЫ |
Лекция |
17/2007 |
Лекция 1. Что такое
“математические основы информатики”. Почему
информатику нередко считают близкой род-
ственницей математики? Верно ли это? Возможна ли
информатика без математики? Какая математика
нужна для освоения
информатики? Может ли школьная математика дать
основу для информатики?
Информация и ее кодирование.
Математика кодов. Коды, исправляющие ошибки.
Экономное кодирование. |
18/2007 |
Лекция 2. Математические модели
формальных исполнителей. Что такое формальная
обработка информации? Конеч-
ные автоматы. Что первично: язык или исполнитель?
Грамматика языка. Распознаваемые языки.
Универсальные исполни-
тели (машина Тьюринга, машина Поста). |
19/2007 |
Лекция 3. Алгоритм и его
свойства. Алгоритмическая неразрешимость.
Вычислимость. Сложность. |
| Контрольная работа № 1. |
20/2007 |
Лекция 4. Графы. Графы и орграфы. В каких
задачах они возникают? Различные свойства графов
(эйлеровость, гамильто-
новость, планарность, двудольность). Сети. Потоки
в сетях. Представление графов. Основные
алгоритмы на графах. |
21/2007 |
Лекция 5. Логические модели в информатике.
Алгебра высказываний. Булевы функции.
Нормальные формы. Полные
классы булевых функций. Релейно-контактные
схемы. Вентили. Математические модели процессора
и памяти компьютера. Предикаты и отношения.
Реляционная алгебра. Теоретические основы
реляционных СУБД. Языки логического
программирования и их математическое основание. |
| Контрольная работа № 2. |
22/2007 |
Лекция 6. Компьютерная теория чисел и
вычислительная геометрия. Зачем нужна теория
чисел в компьютерных
науках? Гонка за простыми числами. Как разложить
число на множители? Чем отличается теоретическая
геометрия от
вычислительной? Почему гладко на бумаге, но
коряво на компьютере? Основные правила и
алгоритмы вычислительной
геометрии. |
| 23/2007 |
Лекция 7. Защита информации. Защита
символьной информации. Что нужно защищать?
Электронная подпись. Системы
верификации. Криптосистемы с открытым ключом.
Защита графической информации. Математика
электронных водяных знаков. |
| 24/2007 |
Лекция 8. Основы методики преподавания
математических основ информатики. |
| Итоговая работа |
Лекция 3. Алгоритм и его свойства.
Алгоритмическая неразрешимость
Формальная обработка информации —
это, как было сказано в лекции 2, четкое и
бездумное следование инструкции, предписывающей
исполнителю выполнение определенной
последовательности действий. Конечно, такие
инструкции могут быть устроены по-разному. К
примеру, для машины Тьюринга инструкция,
определяющая обработку информации, представлена
функциональной схемой. Но каждый, кто попытался
“влезть в шкуру” машины Тьюринга (например,
выполняя задания к § 4 лекции 2), ощутил, насколько
далека от человеческой логика такой инструкции.
Для нас намного естественнее инструкции, в
которых в явном виде предъявлена
последовательность осуществления заданных
действий. Такого типа инструкцию называют
алгоритмом.
Разумеется, алгоритмы — вовсе не
изобретение ХХ века, когда появились первые
электронно-вычислительные машины. Они даже
намного древнее своего названия, произошедшего
от искажения слов “аль-Хорезми”. Некоторые из
них навсегда ушли из человеческой практики.
Никто, например, сейчас не производит действия с
дробями по тем алгоритмам, которые применялись
древними египтянами. Другие алгоритмы, столь же
давно изобретенные, и сегодня играют важную роль.
Примером тому служит всем известный алгоритм
Евклида вычисления наибольшего общего делителя
натуральных чисел. (Евклид, конечно, и не
догадывался, что придуманный им способ
называется алгоритмом.) А вот сказать, что такое
алгоритм, оказалось непросто. А надо. И дело не
только в том, что требуется как-то отличать
алгоритмы от всяческих инструкций другого рода.
Важнее уметь для имеющейся задачи определять,
существует ли алгоритм, ее решающий. Обычно, если
алгоритм есть и нам его предъявляют, то ни у кого
нет сомнения в том, что все в порядке1. А вот
как доказать отсутствие алгоритма, если не
знаешь, что это такое?
Математика и здесь оказалась наиболее
востребованной. Основных причин для этого,
по-видимому, две. Во-первых, само это понятие
формировалось именно в сфере действий над
математическими объектами: числами (как целыми,
так и дробными), алгебраическими выражениями,
геометрическими фигурами и величинами.
Во-вторых, именно в математике развивались
методы строгих доказательств, приведшие в
конечном счете к появлению особой дисциплины —
математической логики. Мы поэтому тоже при
изучении алгоритмов ограничимся сферой
математических рассмотрений.
§ 5. Понятие алгоритма. Свойства
алгоритмов
Довольно стандартное определение
алгоритма, которое бытует в школьных учебниках
информатики, таково: “Алгоритм — это
последовательность допустимых для некоторого
исполнителя действий, направленная на
достижение определенной цели”. Вполне
пристойное определение, ничуть не хуже, чем
определения, даваемые в большинстве
естественно-научных дисциплин2. Проблема,
однако, в том, что при таком определении
существование или несуществование алгоритма
зависит от выбора исполнителя. Вот иллюстрация
этой ситуации на геометрическом материале.
Всем известен алгоритм построения с
помощью циркуля и линейки перпендикуляра к
прямой, проходящего через данную точку. Слова “с
помощью циркуля и линейки” — это и есть краткое
задание допустимых действий исполнителя. А вот
если исполнитель вооружен только одной линейкой,
то нетрудно доказать, что с помощью и при
посредстве только этого инструмента построить
перпендикуляр уже невозможно. В свою очередь, с
помощью циркуля и линейки нельзя решить задачу
удвоения куба, т.е. построить куб, объем которого
в точности в два раза больше объема данного куба.
Но если к циркулю и линейке добавить еще
какие-либо инструменты (т.е. расширить список
допустимых действий), то эта задача станет
разрешимой. К примеру, данная задача будет
решаться, если добавить всего лишь возможность
использовать два угольника. Между прочим, после
этого станет возможным решить и другую
знаменитую задачу — выполнить трисекцию угла.
Создается ощущение, что вопрос о существовании
алгоритма, решающего ту или иную задачу, — это
вопрос о наборе допустимых действий
используемого исполнителя.
Ощущение, однако, оказывается
обманчивым. Подробно мы обсудим это в § 9. А сейчас
попробуем найти путь, который позволил бы
обсуждать алгоритмы, не обращаясь явно к понятию
исполнителя. Иными словами, изучить общие
свойства алгоритмов.
Методологической подоплекой
появления понятия “свойства алгоритмов”
является идея объявить, что сам алгоритм —
понятие неопределяемое. В “Математической
энциклопедии” в статье “Алгоритм” про него
именно так и сказано3. Аналогия с другими
математическими теориями (например, геометрией),
где существование неопределяемых понятий
заложено в основу соответствующей теории, а
понятия описываются своими свойствами и
связывающими их соотношениями — аксиомами4,
подсказывает идею описать понятие алгоритма
через его свойства. Именно она легла в основу
большинства школьных учебников информатики (и
нашла свое отражение в Стандарте). Список свойств
невелик: дискретность, массовость, конечность,
результативность, детерминированность. Однако
далеко не всегда бывает легко убедиться в том,
что предложенный алгоритм обладает требуемым
свойством и дает нужный результат. Но сначала
расшифруем, что означает каждое из свойств.
Дискретность. Под дискретностью
понимается то, что алгоритм состоит из описания
последовательности тактов обработки,
организованной таким образом, что в начальный
момент задается исходная ситуация, а в каждый
следующий момент ситуация преобразуется на
основе данных, полученных в предшествующие такты
обработки. Дискретность алгоритма означает, что
он исполняется по шагам: каждое действие,
предусмотренное алгоритмом, исполняется только
после того, как закончилось исполнение
предыдущего.
Детерминированность. Это свойство
означает, что на каждом шаге исполнения
алгоритма (см. свойство дискретности) однозначно
определено преобразование объектов среды
исполнителя, полученных на предшествующих шагах
алгоритма. По-другому это свойство алгоритма
называют точностью.
Результативность. Это свойство
подразумевает, что каждое действие в алгоритме
после своего завершения создает ситуацию, в
которой все имеющиеся объекты однозначно
определены. Если это по каким-либо причинам
невозможно, то алгоритм должен сообщить, что
решение задачи не существует. Это свойство
является обязательным для любого алгоритма.
Обычно говорят о результативности
алгоритма в целом, подразумевая, что алгоритм
предназначен для решения той или иной задачи. Как
правило, одновременно с результативностью в
целом подразумевается и конечность
алгоритма, т.е. завершение его работы за конечное
число шагов (при этом количество шагов может быть
заранее неизвестным и различным для разных
начальных ситуаций).
То свойство алгоритма, что в нем могут
использоваться только допустимые действия
исполнителя, нередко называют понятностью
алгоритма (иногда эффективностью или элементарностью
действий). Понятность является обязательным
свойством любого алгоритма.
Массовость. С точки зрения
практической ценности алгоритма важно, чтобы
множество допустимых начальных ситуаций было
для него достаточно большим (иногда говорят,
потенциально бесконечным). Например, известный
из начальной школы алгоритм сложения столбиком
двух натуральных чисел является массовым,
поскольку применим к любой паре натуральных
чисел.
Несмотря на вышесказанное, мы хотим
предостеречь учителя от чрезмерного внимания к
изучению свойств алгоритмов. Развитие
компьютерной техники, теории алгоритмов и
практики программирования вносит свои
коррективы. Теперь, к примеру, рассматривается не
только последовательное, но и параллельное
исполнение шагов алгоритма (сравним с трактовкой
свойства дискретности). Алгоритм не обязан быть
детерминированным — на очередном шаге может
осуществляться случайный выбор из некоторого
множества возможных результатов. Теория
недетерминированных алгоритмов — современная
бурно развивающаяся ветвь общей теории
алгоритмов. Тем не менее многие
недетерминированные алгоритмы приводят к
однозначно определенному результату. Такие
алгоритмы называют однозначными.
Конечность алгоритма — это тоже
свойство, присущее далеко не всем алгоритмам,
используемым на практике. Почти все алгоритмы,
применяемые для управления объектами в режиме
реального времени, не являются конечными: трудно
представить себе конечный алгоритм (т.е.
прекращающий работу через конечное число шагов)
компьютерного управления полетом космической
станции или работой ядерного реактора. Конечно,
такие алгоритмы, как правило, включают в себя
режим ожидания вмешательства человека (нажатия
той или иной клавиши, щелчка мыши и т.п.), но по
своему устройству такой алгоритм не является
конечным5. Впрочем, бесконечно исполняемые
алгоритмы играют важную роль в общей теории
алгоритмов. Вот пример такого алгоритма,
приведенный в Математической энциклопедии6.
Исполнитель обрабатывает слова, записываемые в
алфавите из двух букв — a и b. Допустимые
действия исполнителя — это переход от слова X
к слову Y в одном из двух случаев:
а) если X имеет вид аР, где Р
— любое слово над данным алфавитом, то Y = Pb;
б) если X имеет вид bаР, где Р
— любое слово над данным алфавитом, то Y = Paba.
Сам алгоритм выглядит так:
алг Слова (арг сим
Х, рез сим Y)
нач
ввод X;
Y := X;
нц пока не получится
слово Y,
начинающееся буквосочетанием bb,
применить к слову Y то действие,
которое можно применить,
и результат обозначить снова Y;
кц
вывод Y
кон
Применим этот алгоритм к слову babaa.
Цикл должен исполняться, поскольку выполнено
условие продолжения цикла. К самому этому слову
применимо только второе допустимое действие.
Поэтому после первого исполнения тела цикла
получаем baaaba. Условие продолжения цикла
снова выполнено, так что при очередном его
исполнении получим aabaaba и т.д. Результатом в
данном алгоритме будет слово bbabababa. Однако
если применить этот алгоритм к слову baaba, то
алгоритм будет исполняться бесконечно.
Фактически свойства алгоритмов играют
такую же роль, как, например, свойства функций:
функция может быть монотонной, а может и не быть;
может быть непрерывной, а может и не быть. Если
функция монотонна — это хорошо, если непрерывна
— еще лучше, но если и не такая, то в этом тоже нет
никакой трагедии. Так и алгоритмы: если они
обладают указанными свойствами — хорошо, а не
обладают (разумеется, на законных основаниях) —
печалиться не следует. В какой мере обсуждать
данные вопросы с учениками — решать учителю;
одно только можно утверждать уверенно: все
алгоритмы, составляемые учащимися в ходе
изучения курса информатики, должны обладать
всеми перечисленными свойствами.
Вопросы и задания
1. Перечислите свойства, которые обычно
рассматриваются для алгоритма. Какие из этих
свойств обязательно должны присутствовать?
2. Исполнитель имеет следующие
допустимые действия:
— стереть с доски два числа и вместо
них написать одно, равное их сумме, увеличенной
на 1;
— сосчитать количество чисел на доске;
— сравнить два натуральных числа.
Рассмотрите следующий алгоритм.
алг Суммирование+
нач
нц пока (на доске более
одного числа)
Стереть какие-нибудь два числа
и вместо них записать их сумму,
увеличенную на 1
кц
кон
а) Объясните, почему этот алгоритм не
является детерминированным.
б) Будет ли этот алгоритм однозначным?
3. Для алгоритмов, приведенных ниже в
пунктах а) – г), постарайтесь описать множество
тех начальных ситуаций, для которых данный
алгоритм результативен.
а)
алг Суммирование_1 (арг цел
N, рез вещ S)
нач цел K
ввод N
S := 0
нц для K от 1 до
N
S := S + K
кц
вывод S
кон
б)
алг Преобразование_в_вопрос (арг
сим С, рез сим А, В)
нач
ввод С
А := С + " " + "goes to school."
B := "Does" + " " + С + " " + Часть
(А, 1, 2) + Часть (А, 5, 10) + "?"
вывод А, В
кон
в)
алг Суммирование_2 (арг цел
N,
арг вещ a, b,
рез вещ S)
нач цел: K, вещ d
ввод a
ввод b
ввод N
d := (b — a)/N
S := 0
нц для K от 1 до
N
S := S + 1/(a + d * K)
кц
вывод S
кон
г)
алг Значение функции (арг вещ
а, х)
нач
ввод х
ввод а
если а > 0
то вывод 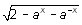
все
кон
4. Ниже в пунктах а) – г) приведены
алгоритмы. Укажите, какие из них обладают
свойством массовости, а какие нет.
а)
алг Суммирование_1 (арг цел
N, рез вещ S)
нач цел K
ввод N
S := 0
нц для K от 1 до
N
S := S + 1/K
кц
вывод S
кон
б)
алг Преобразование_в_вопрос_1 (рез
сим В)
нач сим А
А := "Ann goes to school."
B := "Does" + " " + Часть (А, 1, 6) +
Часть (А, 9, 10) + "?"
вывод В
кон
в)
алг Вычисление_корня (рез вещ
х)
нач
х := 0
нц пока (х3 + 3 * х —
1 < 0)
х := х + 0,01;
кц
вывод Корень равен, х
кон
г)
алг Значение функции (арг вещ
х, рез вещ у)
нач
ввод х
если cos x — 1 і 0
то у := 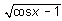
вывод у
все
кон
§ 6. Как доказывают результативность
алгоритма
Рассмотрим следующую задачу.
Задача 1. Последовательность Xn
строится так:
X1 = 1; X2 = 3; ... ; Xn
= Xn-2 — 2Xn-1
для каждого n > 2. Составьте
алгоритм нахождения первого числа в этой
последовательности, большего 100 000.
Каждый из вас легко составит такой
алгоритм. Ясно, что переменные здесь можно
считать имеющими целочисленный тип. Нужный
алгоритм записывается так:
алг Задача_1 (рез вещ
Z)
нач цел X, Y
X := 1
Y := 3
Z := Y
нц пока (Z < 100000)
Z := X - 2 * Y
X := Y
Y := Z
кц
вывод Z
кон
Изменим условие этой задачи.
Задача 2. Последовательность Xn
строится так:
X1 = 1; X2 = 3; ... ; Xn
= Xn-2 – 2Xn-1
для каждого n > 2. Найти первое в
этой последовательности число, большее 100 000.
На первый взгляд кажется, что это та же
задача. Но давайте задумаемся, что является
ответом в каждой их них. В первой это алгоритм, и
он уже приведен выше; во второй ответом служит
число. Значит, это все-таки не одна и та же задача,
хотя ясно, что для решения задачи 2 надо просто
запустить алгоритм, служащий ответом в задаче 1.
И тут возникает вопрос: получим ли мы
ответ, запустив созданный нами алгоритм? Легко
понять, что помешать этому может только одно
отсутствие в данной последовательности хотя бы
одного числа, большего 100 000. Алгоритм же в этом
случае будет исполняться бесконечно,
вырабатывая все новые и новые члены
последовательности.
Что же мы видим? Вопрос о конечности
данного алгоритма оказался равносилен вопросу о
существовании объекта, который этим алгоритмом
строится.
Итак, надо убедиться, что в данной
последовательности встретится хотя бы один раз
число, большее 100 000. Чтобы найти подход к тому, как
в этом можно убедиться, полезно взглянуть на
десяток первых членов последовательности. Вот
эти 10 членов:
1; 3; –5; 13; –31; 78; –181; 437; –1055; 2547.
Глядя на них, можно высказать гипотезу,
что члены с четными номерами положительны и
неограниченно возрастают. Докажем эту гипотезу.
Для этого выразим X2k через
предшествующие члены последовательности с
четными номерами.
X2k = X2k-2 – 2 X2k-1
= X2k-2 – 2 (X2k-3 – 2 X2k-2) =
5 X2k-2 – 2 X2k-3 = 5 X2k-2 – 2
(X2k-5 – 2 X2k-4) = 5 X2k-2 + 4 X2k-4
– 2 X2k-5 = 5 X2k-2 + 4 X2k-4 –
2 (X2k-7 – 2 X2k-6) = 5 X2k-2 + 4 X2k-4
+ 4 X2k-6 – 2 X2k-7 = ... = 5 X2k-2
+ 4 X2k-4 + 4 X2k-6 + ... + 4 X2 –
2 X1.
Поскольку 4X2 – 2X1 =
10, индуктивное рассуждение показывает, что все
члены последовательности с четными номерами
положительны. Более того, теперь ясно, что X2k
> 5 X2k-2. Применяя это неравенство k
раз, получаем: X2k > 5k–1 X2.
Поэтому в данной последовательности имеются
члены, большие не только 100 000, но и вообще любого
положительного числа. Можно сказать, что мы
доказали следующую теорему:
Теорема. Пусть
последовательность Xn определена следующим
рекуррентным соотношением:
X1 = 1; X2 = 3; ... ; Xn
= Xn-2 – 2Xn-1
для каждого n > 2. Тогда для любого
положительного числа M в этой последовательности
существует член, больший чем M.
Заметьте: ни в формулировке теоремы, ни
в ее доказательстве не указывается, каким по
номеру будет искомый член последовательности.
Более того, не намечается даже способ нахождения
нужного члена последовательности. Теоремы, в
которых доказывается существование какого-либо
объекта, обладающего требуемыми свойствами, без
указания способа построения этого объекта
называют теоремами чистого существования. А
теоремы, в которых существование нужного объекта
доказывается указанием способа его построения,
называются конструктивными теоремами
существования.
Вопросы и задания
1. В чем различие между конструктивными
теоремами и теоремами чистого существования?
2. Для решения задачи “В какую
наименьшую натуральную степень надо возвести
число 3, чтобы получилось число, оканчивающееся
на 00001?” был составлен следующий алгоритм:
алг Показатель степени (рез
цел N)
нач цел: X, Y
X := 1
Y := 2
N := 0
нц пока (Y > 1)
X := 3 * X
Y := mod(X, 100000)
N := N + 1
кц
вывод N
кон
а) Объясните, почему данный алгоритм
решает поставленную задачу.
б) Докажите, что данный алгоритм
конечен.
3. Дан алгоритм:
алг Задача_2 (арг вещ
А, Е, рез вещ Х)
нач
ввод А
ввод Е
X := 1
нц пока ABS(X * X - A) 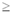 E E
X := (X + A/X)/2
кц
вывод Х
кон
а) Доказать, что при любых
положительных A и E алгоритм завершит свою
работу за конечное число шагов.
б) Попытайтесь оценить количество
шагов в зависимости от А и Е, которое
будет совершено при исполнении этого алгоритма.
4. Рассмотрите следующий алгоритм:
алг Суммирование (рез цел
N)
нач вещ S
S := 1
N := 1
нц пока (S < 20)
N := N + 1
S := S + 1/N2
кц
вывод N
кон
а) Для решения какой задачи
предназначен этот алгоритм?
б) Удастся ли с помощью данного
алгоритма решить эту задачу? (Совет: попытайтесь
установить, закончится ли исполнение этого
алгоритма за конечное число шагов.)
7. Лимитирующая функция
Рассмотрите еще раз те алгоритмы из § 6,
для которых потребовалось доказывать
конечность. Отличительной их чертой является
наличие в них конструкции цикла в форме пока.
Это и понятно — ведь если алгоритм содержит
только линейные фрагменты, конструкции
ветвления и цикла со счетчиком, то исполнение
алгоритма заведомо заканчивается за конечное
число шагов. Конечность алгоритма нужно
обосновывать лишь в том случае, если в нем
используется цикл, для которого заранее
неизвестно количество исполнений тела цикла (т.е.
цикл с предусловием или цикл с постусловием), или
рекурсия. Основным инструментом обоснования
конечности алгоритма в этом случае служит лимитирующая
функция. Так называют переменную величину,
которая каждый раз меняет свое значение при
очередном исполнении тела цикла или рекурсивном
обращении к вспомогательному алгоритму и
обладает следующими двумя свойствами:
— она принимает лишь конечное число
значений (быть может, зависящее от исходных
данных);
— в ходе исполнения алгоритма она
принимает каждое свое допустимое значение не
более одного раза.
Часто лимитирующую функцию выбирают
так, чтобы ее значениями были только натуральные
числа и при каждом исполнении тела цикла ее
значение уменьшалось.
Рассмотрим пример. В учебнике для 10-го
класса мы упоминали знаменитый алгоритм Евклида,
предназначенный для нахождения наибольшего
общего делителя двух натуральных чисел. Вот этот
алгоритм.
алг НОД (арг цел m, n, рез
цел m)
нач
ввод m
ввод n
нц пока не (m = n)
если m > n
то m := m – n
иначе n := n – m
все
кц
вывод m
кон
Как доказать, что этот алгоритм
действительно вычисляет НОД двух чисел, мы
обсудим в следующем параграфе. А вот почему он
конечен?
Рассмотрим величину k = max {m; n}.
До начала исполнения цикла она имеет некоторое
значение k0. Очевидно, что переменная k
принимает только натуральные значения. Заметим
также, что при каждом исполнении тела цикла
значение величины k обязательно уменьшается.
Но натуральных чисел, меньших числа k0,
лишь конечное число. Значит, исполнение тела
цикла не может осуществляться более чем k0
раз. Следовательно, и весь алгоритм заканчивает
свою работу за конечное число шагов, какими бы ни
были начальные натуральные значения m и n.
Впрочем, известны весьма простые
алгоритмы, для которых решение вопроса о
конечности весьма проблематично. Вот алгоритм,
для которого на сегодняшний день не удалось ни
доказать, ни опровергнуть гипотезу о его
конечности:
алг Проблемный (рез цел
K)
нач цел n
K := 1;
ввод n;
нц пока n > 1
если n mod 2 = 1
то n := 3 * n + 1
иначе n := n/2
все
K := K + 1
кц
вывод K
кон
Совершенно ясно, что делает этот
алгоритм: если на каком-то шаге получилось четное
число, то оно делится пополам, если нечетное, то
умножается на 3 с последующим прибавлением 1 (т.е.
число становится четным). Тем самым, после такого
увеличения обязательно идет деление пополам и,
быть может, не один раз.
Вопросы и задания
1. Какие алгоритмические конструкции
могут быть причиной для отсутствия у алгоритма
свойства конечности?
2. Какую функцию называют лимитирующей?
3. Как доказывают конечность алгоритма
с помощью лимитирующей функции?
4. а) Рассмотрите алгоритм,
перерабатывающий натуральное число n.
алг Превращение_1 (арг цел
n, рез цел I)
нач
ввод n
I := 1
нц пока n > 1
если n mod 2 = 1
то n := n – 1
иначе n := n / 2
все
I := I + 1
кц
вывод I
кон
Закончится ли исполнение данного
алгоритма за конечное число шагов? Ответ
обоснуйте.
б) Рассмотрите еще один алгоритм,
перерабатывающий натуральное число n.
алг Превращение_2 (арг цел
n, рез цел I)
нач
ввод n
I := 1
нц пока n > 1
если n mod 2 = 1
то n := n + 5
иначе n := n / 2
все
I := I + 1
кц
вывод I
кон
Закончится ли исполнение этого
алгоритма за конечное число шагов? Ответ
обоснуйте.
5. Предположим, что исполнитель
обладает способностью за одно действие написать
весь натуральный ряд, а также вычеркнуть из него
все числа, удовлетворяющие какому-либо условию,
даже если этих чисел бесконечно много.
Рассмотрите следующий алгоритм для этого
исполнителя:
алг Решето
нач
Написать весь натуральный ряд;
Вычеркнуть из него число 1;
нц пока (есть
необведенные числа среди невычеркнутых)
Среди невычеркнутых чисел обвести
самоемаленькое из необведенных;
Из необведенных чисел вычеркнуть те,
которые кратны последнему обведенному числу;
кц
вывод обведенные числа;
кон
а) Конечен ли этот алгоритм? Ответ
обоснуйте.
б) Попытайтесь определить, для чего
предназначен этот алгоритм, придуманный
древнегреческим математиком Эратосфеном.
Докажите вашу гипотезу (если, конечно, она
окажется верной).
Обоснование результативности
алгоритма нередко подразумевает выявление (и
доказательство) того, что именно является
результатом исполнения алгоритма.
Рассмотрим, к примеру, следующий
алгоритм.
алг проба (арг цел k,
арг вещ а, рез вещ b)
нач цел n, вещ c
ввод k;
ввод a;
b := 1;
n := k;
c := a;
нц пока n > 0
если (n mod 2 = 0)
то c := c * c
n := n/2
иначе b := b * c
n := n – 1
все
кц
вывод b
кон
Как вы думаете, для чего предназначен
этот алгоритм? Гипотез может быть много. И в любую
из них можно поверить. Можно, конечно, взять
конкретные два числа и исполнить для них
алгоритм. Вера в высказанную гипотезу от этого
испытания может либо возрасти, либо мы убедимся,
что гипотеза неверна.
Можно взять много разных пар чисел и на
них проверить высказанную гипотезу. Но все равно
это не будет доказательством, что алгоритм
предназначен именно для того, что было заявлено.
Как же изучать алгоритмы доказательно?
Исследовать алгоритмы, в которых нет
циклов и рекурсии, в общем-то легко: в них каждое
действие исполняется не более одного раза. Для
такого алгоритма можно просто составить
протокол исполнения, записывая результаты
последовательного исполнения всех действий.
С циклами и рекурсией все обстоит
сложнее — далеко не всегда можно указать
конкретное число исполнений тела цикла или
обращений к рекурсивной подпрограмме: оно само
может оказаться переменной величиной.
Поэтому поступают так. Отыскивают
какое-либо свойство объекта, обрабатываемого
алгоритмом, такое, которое не меняется при
исполнении тела цикла. Такое свойство называют инвариантом
цикла. Если таким объектом является некоторый
набор величин, то инвариант цикла нередко
разыскивают в виде соотношения между этими
величинами.
Рассмотрим для цикла, записанного в
нашем алгоритме, величину bcn. До начала
цикла она равна ak. А теперь составим
протокол исполнения тела цикла (см. табл. 1).
Таблица 1

Итак, мы проверили, что величина bcn
— инвариант цикла. Это значит, что все время bcn
= ak, в том числе и после выхода из цикла.
Что же мы будем иметь по окончании
работы цикла? Чтобы понять это, нужно посмотреть
условие окончания цикла (а вовсе не проделывать
все операции в цикле, как могут подумать
некоторые).
Это условие: n > 0. Значит, по
окончанию исполнения цикла n = 0. Но тогда
справедливо равенство bc0 = ak.
Следовательно, после исполнения цикла b = ak,
и именно это значение b сообщит алгоритм
накануне своего завершения.
Вот мы и выяснили (более того,
доказали), что является результатом алгоритма.
Конечно, чтобы убедиться в наличии у этого
алгоритма свойства результативности, надо еще
доказать его конечность. Мы надеемся, что вы
легко сделаете это самостоятельно, указав
подходящую лимитирующую функцию.
1. Что такое инвариант цикла?
2. Рассмотрите следующий алгоритм,
обрабатывающий натуральное число k.
алг Нечто (арг цел k,
рез цел m)
нач цел n
ввод k
m := 0
нц для n от 0 до
k
m := m + 2 * n + 1
кц
вывод m
кон
Для чего предназначен данный алгоритм?
Выдвинутую гипотезу докажите.
3. Рассмотрите следующий алгоритм,
обрабатывающий натуральные числа m и n.
алг Загадка (арг цел
m, n, рез цел x, y)
нач цел u, v
ввод m
ввод n
x := m
y := n
u := m
v := n
нц пока (x < y) или
(x > y)
если x < y,
то y := y – x
v := v + u
иначе x := x – y
u := u + v
все
кц
y := (u + v)/2
вывод x, y
кон
а) Конечен ли этот алгоритм? Ответ
обоснуйте.
б) Для чего предназначен данный
алгоритм? Выдвинутую гипотезу докажите.
9. Алгоритмически неразрешимые задачи
Умение эвристически решать многие
задачи, т.е. не зная никакого алгоритма, —
чрезвычайно важная способность человека.
Например, задачу определения, кто изображен на
фотографии — корова или лошадь, человек решает с
высоким процентом правильных ответов. Однако
никакого алгоритма, позволяющего решить такую
задачу, на сегодняшний день нет. Слишком слабы
наши возможности формализации этой задачи.
Может показаться, что проблема
создания алгоритма для решения задачи упирается
именно в неумение до поры до времени
формализовать стоящую перед нами задачу.
Оказывается, однако, что это не так. Речь, конечно,
идет о так называемой “массовой задаче”, т.е. о
целом множестве однотипных задач, для решения
которых применяется один и тот же алгоритм.
Напомним, что свойство алгоритма, состоящего в
возможности его применения к решению однотипных
задач, называется массовостью. Приведем пример
такой задачи.
Рассмотрим множество алгоритмов,
предназначенных для обработки символьной
переменной х (т.е. в качестве входного данного
для алгоритма выступает некоторый текст).
Представим все эти алгоритмы записанными на
каком-либо языке программирования. Задача
состоит в том, чтобы по тексту алгоритма и
значению х узнать, закончит ли этот алгоритм
работу над данным значением х за конечное
число шагов.
Эту задачу называют задачей об
останове. Оказывается, что для этой задачи не
существует алгоритма ее решения. Но прежде чем
доказывать отсутствие алгоритма, обсудим роль
этой задачи для теории алгоритмов в целом.
Отметим в первую очередь, что в этой
задаче речь идет о формальной обработке текстов.
Следовательно, исполнители, для которых
составляются такие алгоритмы, — это устройства,
преобразующие один текст в другой, например,
машина Тьюринга. Впрочем, и любой компьютер
занимается ровно тем же самым — ведь он
преобразует одну поступающую к нему
последовательность сигналов в другую. А всякая
последовательность сигналов, кодируемых
символами некоторого алфавита, это и есть текст.
Нетрудно понять, что вообще любая формальная
обработка символьной информации — это
преобразование текста по заданным формальным
правилам. Поэтому, говоря об алгоритмах,
обрабатывающих текст, мы фактически ведем речь о
формальной обработке любой информации. Отметим,
что при этом нам совершенно неважно, насколько
“богат” набор допустимых действий исполнителя,
используемого для обработки текста.
Теорема. Не существует алгоритма
решения задачи об останове.
Докажем эту теорему, рассуждая и на
этот раз от противного.
Пусть существует алгоритм решения
этой задачи (это, конечно, подразумевает, что
существует и исполнитель, для которого создан
такой алгоритм; ясно, что данный исполнитель
способен обрабатывать любые тексты). Назовем его
алгоритмом А. Через В обозначим
произвольный алгоритм из указанного множества
алгоритмов. Входными данными для алгоритма А
служат текст алгоритма В и значение
символьной переменной х. Договоримся, что в
результате своей работы алгоритм А
присваивает некоторой переменной z значение
1, если алгоритм В заканчивает работу на
тексте х за конечное число шагов, и значение
0 в противном случае. Иными словами, алгоритм А
выглядит так7:
алг А (арг сим В, х; рез
цел z)
нач
ввод B
ввод х
если (алгоритм В заканчивает
работу на тексте х за конечное число шагов)
то z := 1
иначе z := 0
все
кон
Рассмотрим множество алгоритмов,
которые в качестве допустимого значения х
берут свое описание на указанном языке
программирования. Построим алгоритм С,
принадлежащий этому классу:
алг С (арг сим В)
нач цел: z
ввод B
z = 1
нц пока z = 1
вызвать А(В, B, z)
кц
кон
Запустим составленный нами алгоритм С
на исполнение. На запрос значения В введем
текст алгоритма С. На следующем шаге
переменной z будет присвоено значение 1,
поэтому затем начнется исполнение тела цикла.
Что же произойдет после обращения к
вспомогательному алгоритму А?
Допустим, что алгоритм С конечен.
Тогда после исполнения алгоритма А значение z = 1.
Поэтому начнет исполняться тело цикла. Однако в
результате исполнения в теле цикла того же
вспомогательного алгоритма значение переменной
z не изменится. Поэтому тело цикла будет
исполняться бесконечное число раз и,
следовательно, алгоритм С конечным не
является. Значит, такая ситуация невозможна.
Допустим теперь, что алгоритм С
конечным не является. Тогда после исполнения
алгоритма А значение z = 0. В этом
случае тело цикла больше не будет исполняться, и,
следовательно, алгоритм С прекратит работу
за конечное число шагов. Следовательно, и в этом
случае получилось противоречие. Значит,
предположение, что существует алгоритм А,
было ложным.
Грустным следствием этого утверждения
является тот факт, что невозможно создать
универсальный алгоритм отладки программы. Иными
словами, никто, кроме вас самих, программу не
отладит.
Задачи, для которых не существует
алгоритма решения, называются алгоритмически
неразрешимыми. Сегодня известно уже довольно
много алгоритмически неразрешимых задач. И, как
правило, доказательство их алгоритмической
неразрешимости отнюдь не такое простое, как для
рассмотренного нами примера. Одна из самых
знаменитых задач была сформулирована в 1900 году
Давидом Гильбертом на Всемирном математическом
конгрессе. Всего он сформулировал 23 проблемы,
решение которых, как он считал, определит лик
математики ХХ века. И действительно, решение,
даже частичное, любой из его проблем
рассматривается как высшее математическое
достижение. Проблема под номером 10 звучит так:
“Дано произвольное уравнение Р(х1, х2,
…, хn) = 0, где Р(х1, х2,
…, хn) — многочлен с целыми
коэффициентами от указанных переменных.
Существует ли алгоритм, позволяющий выяснить,
имеет ли это уравнение решение в целых числах?”
Лишь спустя 70 лет наш соотечественник
Ю.В. Матиясевич доказал, что такого алгоритма
не существует.
Хочется, однако, знать не только то,
разрешима алгоритмически та или иная задача, но и
вообще как-то описать класс тех задач, которые
алгоритмически разрешимы. Но ведь невозможно
обозреть всех формальных исполнителей, которые
способны обрабатывать информацию! Нужен такой
исполнитель, который один бы мог делать все то,
что делает любой другой формальный исполнитель.
Такого исполнителя мы в §4 назвали универсальным.
Там же мы объявили, что одним из таких
исполнителей является машина Тьюринга. Но это
утверждение доказано быть не может и принимается
в теории алгоритмов как один из важнейших
постулатов. Важным аргументом в его пользу
является то обстоятельство, что любая задача,
которую можно решить с помощью других известных
формальных исполнителей, оказывается разрешимой
с помощью машины Тьюринга. Это позволило в теории
алгоритмов принять следующее определение: “Алгоритмом
называется последовательность действий, которая
может быть записана в виде подходящей
функциональной схемы для машины Тьюринга”.
Есть из этого постулата еще одно
важное следствие. Каждому ясно, что для одной и
той же задачи могут существовать разные
алгоритмы ее решения. Как же сравнить такие
алгоритмы и, например, понять, какой из них
эффективнее? Как сравнить алгоритмы для разных
задач и тем самым установить, какая из них
сложнее с алгоритмической точки зрения? Для
ответа на эти вопросы надо иметь “измерительный
инструмент”, некий эталон, по которому будет
осуществляться сравнение. Благодаря постулату о
машине Тьюринга мы получаем такой эталон: для
каждой задачи среди всех алгоритмов, ее решающих,
выбираем такой, для которого функциональная
схема машины Тьюринга минимальна (в том или ином
смысле). Сравнивая между собой сложность
минимальных функциональных схем для разных
задач, мы получаем объективный критерий
сложности алгоритмического решения самой
задачи.
Конечно, сегодня, обсуждая сложность
алгоритма или его эффективность, никто не пишет
соответствующую функциональную схему. Для этих
целей создан специальный математический
аппарат. Но это уже совсем другая история.
1 Сомнения, конечно, возникают —
то ли делает данный алгоритм, что от него
требуется, при любых ли начальных данных он
работает и т.п. Но это сомнения иного рода: никто
не сомневается в том, что предъявленный нам
объект — это алгоритм.
2 Вот примеры: “Электромагнитная
волна — возмущение электромагнитного поля,
распространяющееся в пространстве” (Касьянов
В.А. Физика, 11-й класс. М.: Дрофа, 2002), “Мельчайшие
структуры, способные к самовоспроизведению,
называются клетками” (Рувинский А.О. и др.
Общая биология, 10–11-е классы. М.: Просвещение, 1993),
“Вирус — это неклеточная форма жизни” (там же).
3 См.: “Математическая
энциклопедия”, ред. И.М. Виноградов. Т. 1. М.:
Советская энциклопедия, 1977, ст. 205. При применении
понятия “алгоритм” в конкретной ситуации оно
соответствующим образом уточняется. С этой целью
в понятии алгоритма выделяется 7 параметров, и в
зависимости от того, как формализуются эти
параметры, получается то или иное уточненное
понятие алгоритма.
4 Одна из наиболее известных аксиом,
связывающая понятия точки и прямой, такова: через
любые две точки можно провести прямую и притом
только одну.
5 В научных кругах обсуждается
вопрос о том, чтобы подобные алгоритмы лишить
“звания” алгоритма и называть их операционной
обстановкой. Однако единой точки зрения на этот
счет пока нет, и решение не принято.
6 Математическая энциклопедия (см. сноску
3) издана в 1977 году. Уже тогда было общепризнано,
что алгоритмы не обязаны обладать свойством
конечности. Тем не менее в школьные учебники по
информатике (которая появилась в школе лишь в 1985
г.) это свойство вошло, и на экзаменах у
выпускников и абитуриентов о нем спрашивают как
об обязательном свойстве алгоритмов.
7 Разумеется, для исполнителя алгоритм
будет записан в виде программы на языке, понятном
этому исполнителю. Но форма представления
алгоритма абсолютно не важна с точки зрения
теории алгоритмов. |