Курсы повышения квалификации
Контрольная работа № 1 по курсу
А.Г. Гейна “Математические основы информатики”
Уважаемые слушатели курсов повышения
квалификации!
Для получения зачета по пройденной
части курса вам необходимо выполнить
контрольную работу № 1. Срок отправки работы
указан в каталоге курсов. Для отправки работы
рекомендуем использовать полученные вами
почтовые этикетки.
Вместе с выполненной работой
необходимо выслать данный бланк или его
ксерокопию.
Выполненную работу необходимо
оформить в виде файла в формате Microsoft Word. Название
файла — персональный идентификатор слушателя.
Программы для заданий 2.6–2.9 представляются в
отдельных файлах с расширением tur в формате
программы “Алго2000”, которую можно получить как
на сайте газеты “Информатика” https://inf.1sept.ru
в разделе “Download”, так и на сайте Педуниверситета
https://edu.1sept.ru на странице данного курса. В
качестве электронных носителей, пожалуйста,
используйте дискеты или CD-R/RW. Кроме электронных
носителей, в обязательном порядке необходимо
представить распечатку файла.
Оценивание работы будет производиться
по системе зачет/незачет. “Вес” каждого вопроса
(пункта) — 1 балл. Исключение составляют задания
2.6–2.9, полный “вес” которых 5 баллов.
Максимальное количество баллов за
контрольную — 50. Для получения зачета необходимо
набрать не менее 26 баллов.
Желаем вам успехов!
К теме “Надежность кодов.
Экономное кодирование”
1.1. Символы a, b, c, d
закодированы следующим образом: a®000000, b®010101,
c®101010, d®111111.
а) Каково минимальное расстояние между
кодовыми словами?
б) Получено сообщение 110101101011001111110000.
Попытайтесь его декодировать, исправив, если
необходимо, ошибки.
1.2. Для кодирования первых 15 букв
русского алфавита и пробела использовался
следующий код:
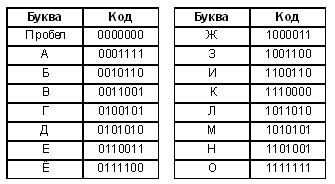
а) Каково минимальное расстояние между
кодовыми словами?
б) Получено сообщение
0101110011000110100101011111001000000111100000111101001
11101001011011101100110010100110111001001101100111101110
Попытайтесь его декодировать,
исправив, если необходимо, ошибки. Все ли символы
удалось расшифровать однозначно? Какая фраза, на
ваш взгляд, здесь закодирована?
1.3. Дан набор кодовых слов: 00, 10, 010, 101, 110,
1001, 1011, 1101, 1111. Постройте для этого кода
соответствующий ему орграф. Является ли этот код
префиксным?
1.4. а) Постройте код Хаффмана для фразы
“ОТ ТОПОТА КОПЫТ ПЫЛЬ ПО ПОЛЮ ЛЕТИТ”.
б) Определите коэффициент сжатия для
данной фразы, если каждый символ кодируется в ASCII.
К теме “Математические модели
формальных исполнителей”
2.1. Для автомата, изображенного на рис.
1, определите, в каком состоянии он будет
находиться после исполнения последовательности
команд
а) babab;
б) anbт+1, где n 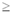 0; 0;
в) a(bab)n, где n 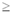 0. 0.
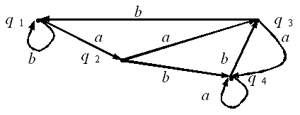
Рис. 1
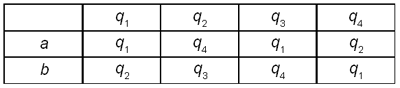
2.2. Изобразите в виде схемы автомат,
заданный таблицей.
2.3. Среди перечисленных ниже множеств L1,
L2, L3, L4, L5,
состоящих из слов над двухсимвольным алфавитом
{1; 2}, укажите распознаваемые языки. Для каждого из
распознаваемых языков постройте распознающий
его автомат; для каждого из остальных множеств
докажите нераспознаваемость.
а) L1 состоит из всех слов,
которые представляют собой нечетные натуральные
числа, начинающиеся с цифры 2;
б) L2 состоит из всех слов, у
которых первая и последняя цифры различны;
в) L3 состоит из всех слов,
которые одинаково читаются слева направо и
справа налево;
г) L4 состоит из всех слов,
количество единиц в которых четно, а количество
двоек нечетно;
д) L5 состоит из всех слов,
количество единиц в которых ровно в два раза
больше количества двоек.
2.4. Работа машины Тьюринга описана
следующей функциональной схемой:
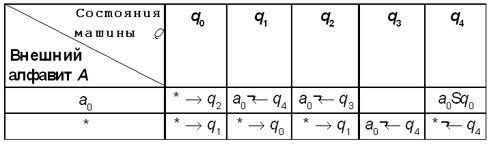
Определите, какое сообщение будет на
ленте после окончания работы машины, и укажите
(например, * над ячейкой), напротив какой ячейки в
этот момент будет находиться ее пишущий блок.
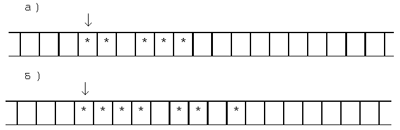

2.5. На ленте машины Тьюринга записана
строка, состоящая из символов “*” и символов “#”
(вперемежку без пробелов). Один из возможных
вариантов такой строки приведен на рис. 2.

Рис. 2
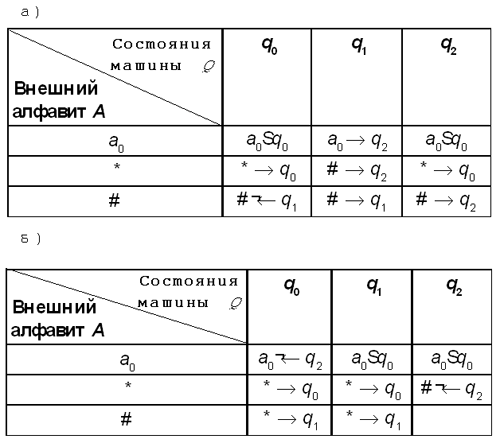
Для каждой из приведенных ниже
функциональных схем определите, для решения
какой задачи она предназначена. В качестве
ответа укажите закономерность, связывающую
исходную последовательность с результирующей.
Задания 2.6–2.9 будут проверяться
тестированием на имитаторе машины Тьюринга
“Алго2000” с помощью системы тестов. Каждый тест в
зависимости от сложности оценивается некоторым
числом баллов. Сумма баллов по всем тестам одного
задания равна 100. Оценка за выполнение задания
определяется делением на 20 набранной суммы
баллов за правильно прошедшие тесты. Считается,
что на ленте первоначальная информация записана
корректно (т.е. в точности соответствует условию).
Дополнять внешний алфавит символами, не
указанными в условии задачи, запрещено.
Количество внутренних состояний — на усмотрение
решающего задачу.
2.6. Пусть внешний алфавит состоит из
символа “a0”, цифр 0, 1, 2, ..., 9 и символа
“*”. На ленту записано натуральное число в
двоичной системе счисления. Составьте
функциональную схему для машины Тьюринга, с
помощью которой на ленте будет записано то же
число в десятичной системе. Ответ требуется
записать правее исходного числа, отделив от
числа символом “*”.
2.7. На ленте записана
последовательность из n символов “*” (n –
натуральное число). Составьте функциональную
схему для машины Тьюринга, с помощью которой на
ленте вместо исходной последовательности будет
записана последовательность из [(n + 1)/2]
звездочек. (Квадратные скобки обозначают целую
часть числа.)
2.8. Пусть внешний алфавит состоит из
символа “a0”, цифр 0, 1, 2, ..., 9, а также
символов “+” и “=”. На ленту записан пример на
сложение двух натуральных чисел в десятичной
системе счисления. Образец:
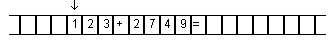
Составьте функциональную схему для
машины Тьюринга, с помощью которой на ленте будет
записана сумма этих чисел. Ответ требуется
записать после знака “=”.
2.9. Пусть внешний алфавит состоит из
символа “a0”, цифр 0, 1, 2, ..., 9, а также
символов “–” и “=”. На ленту записан пример на
вычитание двух натуральных чисел в десятичной
системе счисления. Образец:
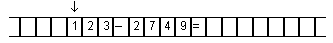
Составьте функциональную схему для
машины Тьюринга, с помощью которой на ленте будет
записана разность этих чисел (она может
оказаться отрицательным числом!). Ответ
требуется записать после знака “=”.
К теме “Алгоритм и свойства
алгоритма”
В приведенных ниже заданиях ваш ответ
о том, конечен или нет предложенный алгоритм,
требуется обосновать.
3.1. Дан алгоритм:
алг Последовательность (арг
цел М, рез цел Z)
нач цел: X, Y
ввод М;
X := 1
Y := 3
Z := Y
нц пока Z < М
Z := Y - 2 * X
X := Y
Y := Z
кц
вывод Z
кон
Верно ли, что при любом целом М этот
алгоритм конечен?
3.2. Рассмотрите следующий алгоритм:
алг Сумма (арг цел
М, рез цел N)
нач вещ: S
S := 1
N := 1
вывод "Введите натуральное
число М"
ввод М
нц пока S < М
N := N + 1
S := S + 1/N
кц
вывод N
кон
а) Для решения какой задачи
предназначен этот алгоритм?
б) Ясно, что при М = 1 тело цикла не
выполняется ни разу и, следовательно, алгоритм
конечен. При любом ли значении М данный алгоритм
конечен?
3.3. Рассмотрите следующий алгоритм,
преобразующий натуральные числа.
алг Преобразование (арг цел
а, b, n, рез цел m)
нач
ввод n
ввод а
ввод b
m := n
нц пока (m 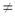 a) и (m a) и (m 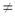 b) b)
m : = СКВ(m)
кц (*конец цикла*)
вывод m
кон
алг цел СКВ (арг цел
n)
нач
если n < 10
то знач := n * n
иначе знач := СКВ (n div 10) +
(n mod 10)*(n mod 10)
все
кон
При каких a и b этот алгоритм
конечен? Перечислите все возможные здесь
варианты.
3.4. Дан алгоритм:
алг Накопительный (арг цел
K, М)
нач
ввод K
ввод М
нц пока (K mod 2 = 0 или
M mod 2 = 0)
если K mod 2 = 0
то M := M + K/2
все
если M mod 2 = 0
то K := K + M/2
все
кц
вывод M + K
кон
Определите, для каких пар натуральных
чисел K и М этот алгоритм завершает работу за
конечное число шагов.
3.5. Рассмотрите следующий алгоритм.
алг Половинчатый (арг цел
K, М)
нач
ввод K
ввод М
нц пока (K mod 2 = 0 или
M mod 2 = 0)
если K mod 2 = 0
то K := K/2
M := M + K
все
если (M mod 2 = 0)
то М := M/2
M := M + K
все
кц
вывод M * K
кон
Определите, для каких пар натуральных
чисел K и М этот алгоритм завершает работу за
конечное число шагов.
3.6. Дан массив М[1:30], состоящий из
положительных чисел. Рассмотрите следующий
алгоритм. Через RND(1) здесь обозначен датчик
случайных чисел, при обращении к нему он
вырабатывает случайное число из [0; 1).
алг Случайность (арг вещ
таб М[1:30])
нач вещ: x, y, цел:
I, J
нц I от 1 до 30
ввод M(I)
кц
у := 1
нц пока у > 0
I := INT (30*RND (1)) + 1
J := INT (30*RND (1)) + 1
x := (M(I) + M(J))/2
y := ABS(M(I) – M(J))/2
M(I) := x
M(J) := y
кц
вывод "Случайность не
помеха"
кон
а) Определите, будет ли этот алгоритм
конечным, если массив М содержит только
натуральные числа.
б) Будет ли конечным этот алгоритм,
если массив М состоит из произвольных
положительных чисел?
3.7. Даны два массива К и М с
целочисленными элементами, расположенными в
каждом из них в порядке возрастания. Рассмотрите
следующий алгоритм:
алг Количество (арг цел
таб К[1:20], М[1:30], рез цел с)
нач цел: a, b
a := 1
b := 1
c := 1
нц пока (a 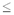 20 и b 20 и b 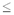 30) 30)
выбор
при K(a) < M(b)
a := a + 1
при K(a) > M(b)
b := b + 1
при K(a) = M(b)
a := a + 1
b := b + 1
c := c + 1
все
кц
вывод c
кон
а) Для решения какой задачи
предназначен этот алгоритм?
б) Найдите подходящий инвариант и докажите
гипотезу, выдвинутую вами при выполнении пункта
а). |