СТРАНИЦЫ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

Математические основы информатики: из неопубликованного

А.Г. Гейн,
г. Екатеринбург

В рамках Педагогического университета “Первое сентября” в газете “Информатика”, начиная с № 17 за 2007 год, публиковались лекции курса с тем же названием. По замыслу автора каждая лекция была введением в то или иное направление этой довольно большой и весьма многоликой области математико-информатического знания. Получается, что в конце каждой лекции подразумеваются слова “Продолжение следует”, а его нет, потому что новая лекция открывает новое направление. Вот теперь, уже вне рамок Педагогического университета, мы предлагаем вниманию читателей эти продолжения*.

Математические основы кодирования информации

В лекции 1 было рассмотрено кодирование символьной информации, при этом основное внимание уделено двум вопросам — обнаружению и исправлению ошибок, возникающих при передаче сообщений, и экономичности кодирования, в частности, алгоритмам сжатия символьной информации. Но сегодняшний мир компьютерных технологий немыслим без информации, передаваемой видео- и аудиосредствами. Какова математическая подоплека этих способов представления информации — вот о чем пойдет речь ниже.

§ 1. Кодирование цветной информации

Прежде всего кратко повторим то, что вам скорее всего и так известно о кодировании графической информации. Во-первых, для кодирования любое изображение подвергается дискретизации, т.е. разбиению на маленькие части. Во-вторых, цвет каждой такой части описывается тем, “сколько” нужно взять каждого из основных цветов — красного, зеленого и синего, — чтобы, смешав их, получить нужный цвет.

Когда художник рисует картину, оттенки цветов он выбирает по своему вкусу. Но в любом технологическом процессе цвет необходимо стандартизировать, чтобы воспроизводить его совершенно точно и однозначно. Поэтому надо определить, что такое красный, зеленый и синий цвета. Как известно, цвет определяется длиной волны. И вот в 1931 г. 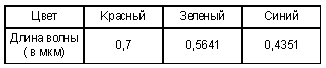в качестве международного стандарта была принята система CIE (Commission Internationale d'Eclairage).
В этой системе три основных цвета стандартизированы так, как показано в табл. 1.

Таблица 1

Стандарты цвета CIE

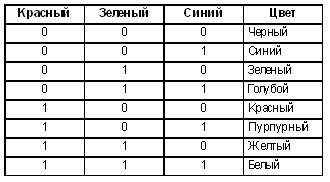
Напомним, какие цвета получаются при смешивании этих цветов в одинаковых пропорциях (см. табл. 2).

Таблица 2

Кодирование основных цветов

Впрочем, для получения того или иного цветового оттенка можно комбинировать и другие цвета, отличные от указанных выше. Этот факт был обнаружен М.В. Ломоносовым в его экспериментах по производству цветных стекол для мозаики и теоретически обобщен Германом Грассманом в виде законов аддитивного синтеза цвета. Слово “аддитивный” означает, что речь идет о смешивании, так сказать сложении, цветов. Мы сформулируем два из них, наиболее важных для понимания сути цветовоспроизведения и цветового кодирования.

Цвета некоторого набора цветов называются независимыми, если никакой из них нельзя получить, смешивая остальные цвета этого набора.

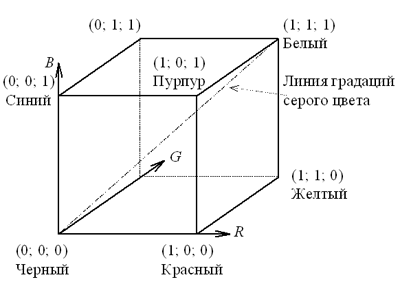
Подчеркнем, что эти законы отражают восприятие цвета человеком. С физической точки зрения цвет характеризуется длиной волны. Еще И.Ньютон разложил белый свет на спектральные составляющие и выделил из них семь наиболее заметных: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. Так что свет желтого цвета — это не смесь красного и зеленого!

Почему же в качестве основных цветов для синтеза цвета на экране компьютера, телевизора и других устройств отображения графической информации выбраны именно эти три цвета? Ответ снова кроется в физиологии человеческого зрения. Как известно, рецепторы человеческого глаза делятся на две группы: палочки и колбочки. Палочки более чувствительны к интенсивности поступающего света, а колбочки — к длине волны. Поэтому восприятием цвета человек обязан именно колбочкам. Если посмотреть, как распределяется количество колбочек по тому, на какую длину волны они “настроены”, то окажется, что наибольшие доли имеют как раз колбочки, воспринимающие синий, зеленый и красный цвета. Естественно эти цвета взять основными и, смешивая их, получать остальные цвета. Согласно закону трехмерности, этих цветов достаточно, а любой цвет задается тройкой чисел (a, b, c), показывающих, в каком соотношении нужно взять эти цвета. Можно при этом считать, что каждое из чисел меняется в диапазоне от 0 до 1, где числу 1 соответствует максимально возможная яркость источника света, передающего данный цвет, а числу 0 соответствует отсутствие света, несущего данный цвет. Обычно при технической реализации данной модели цветопередачи стремятся к тому, чтобы исходная яркость каждого из основных цветов была одинаковой, иначе возникнут искажения (многие, наверно, наблюдали подобные искажения на экранах своих “стареньких” телевизоров, у которых от времени уже произошло рассогласование яркости трех основных цветов).

Указанные три числа можно рассматривать как код любого цвета — ведь они его однозначно определяют. Такой способ кодирования называют RGB-кодированием по первым буквам английских названий трех основных цветов: Red — красный, Green — зеленый и Blue — синий. Еще раз подчеркнем, что данный способ организации цвета связан именно с особенностями человеческого зрения. У собак оно, например, смещено в сине-фиолетовую область (захватывая немножко невидимый для человека ультрафиолетовый спектр). Поэтому человек долгое время считал, что у собак вообще нет цветного зрения. У других животных восприятие цвета смещено, наоборот, в красную и инфракрасную область — они способны видеть даже тепловые лучи. Если бы видеотехнологию разрабатывали такие животные, то у них было бы иное цветовое кодирование.

Описание цвета тройкой чисел наводит на мысль считать эти числа координатами точки в пространстве. Тогда получается, что коды всех цветов заполняют куб с ребром 1. Такой куб изображен на рис. 1. В кодирование цвета вмешалась геометрия.

Рис. 1. Цветовой куб для RGB-кодирования

Яркость цвета определяется тем, насколько близка к 1 хотя бы одна из координат точки, соответствующей данному цвету. А чем ближе точка к диагонали, соединяющей черный и белый цвета, тем меньше насыщенность цвета, обозначенного этой точкой.

Вы уже знаете, что конечность разрядной сетки не позволяет использовать для кодирования информации в компьютере любые числа. По счастью, закон непрерывности позволяет для каждого цвета построить весьма близкое приближение.

В современных компьютерах обычно используется 16-битное (режим Hi-Color) и 24-битное кодирование (режим True-Color). В первом случае оказывается возможным закодировать 2¹⁶ = 65 536 цветов, во втором — 2²⁴ = 16 777 216 цветов. В режиме True-Color на кодирование градаций яркости каждого из основных цветов отводится 1 байт: код 00000000 показывает, что данного цвета нет вообще, а код 11111111 соответствует наибольшей интенсивности (яркости) кодируемого цвета. В случае 16-битного кодирования ситуация иная: на кодирование яркости красного и синего цветов отводится по 5 битов, а на кодирование зеленого цвета — оставшиеся 6 бит. Поэтому в данном режиме шкала яркости для зеленого цвета содержит в 2 раза больше градаций, чем для красного и синего.

Кодирование цвета в режиме True-Color абсолютно обеспечивает качество цветовоспроизведения. Изменение в коде значения одного бита дает настолько незначительное изменение цвета фигуры, что человеческий глаз его не улавливает.

Поскольку именно модель RGB-кодирования соответствует механизму формирования цветного изображения на экране монитора, практически все форматы графических файлов хранят изображение в этой кодировке. Если же используется другая цветовая модель (такое имеет место, например, в формате JPEG), то компьютеру при выводе изображения на экран приходится спешно преобразовывать графические данные в RGB-код.

Выше мы уже сказали, что цвет определяется тем, какой уровень яркости имеет каждый из трех основных цветов. Пусть, для примера, выбрано 64 градации яркости. Занумеруем их от 0 до 63. Легко понять, что наборы градаций (5, 15, 30) и (10, 30, 60) основных цветов дают один и тот же цвет, только разной насыщенности. Каждую из этих троек можно воспринимать как вектор в трехмерном пространстве. Взглянув на “цветовой” куб (рис. 8 из учебника), мы увидим, что эти два вектора сонаправлены, просто один вектор составляет половину второго. Это означает, что цвет (без учета насыщенности) определяется не самими уровнями яркости, а отношением этих уровней (в нашем примере 5 : 15 : 30). Тогда без ограничения общности можно считать, что сумма трех членов отношения равна, скажем, 1. Наш пример тогда запишется как 0,1 : 0,3 : 0,6.

Теперь в изучении представления цвета нам снова поможет геометрия. Путь на координатной плоскости даны три точки — A, B и C. Обозначим координаты точки A через x₁, y₁, координаты точки B через x₂, y₂, координаты точки C через x₃, y₃. Оказывается, что тогда любая точка D, лежащая в треугольнике ABC, имеет координаты u и v, выражающиеся через координаты вершин треугольника с помощью следующих формул:

— где коэффициенты , и неотрицательны и связаны соотношением . И наоборот, каждая точка, координаты которой вычисляются по указанным формулам с неотрицательными коэффициентами, сумма которых равна 1, принадлежит треугольнику ABC. Это наводит на мысль, что, обозначив точками на плоскости три основных цвета, мы можем каждой точке треугольника с вершинами в этих точках сопоставить цвет, получаемый из основных в соответствии с аддитивной моделью цветового кодирования. Такое изображение называют цветовой диаграммой.

В этой системе три основных цвета, стандартизированные по длине волны (см. табл. 1), имеют фиксированные координаты в плоскости XOY (см. табл. 3).

Таблица 3

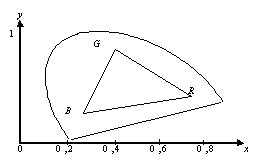
Все цвета, видимые человеком, образуют в плоскости XOY область, изображенную на рис. 2. Основные цвета системы RGB дают вершины внутреннего треугольника. И только цвета этого треугольника можем увидеть мы на экране компьютера, сколько бы градаций каждого из основных цветов ни позволяла видеокарта.

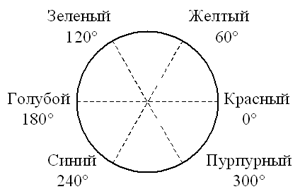
Рис. 2

Если к трем цветам добавить четвертый, не лежащий внутри треугольника, то на цветовой диаграмме все получаемые цвета заполнят уже четырехугольник с вершинами в точках, изображающих эти цвета. Поэтому, добавив в число основных цветов еще несколько, можно расширить палитру цветов, воспроизводимых на экране компьютера. Однако обойдется это весьма недешево. Кроме того, сколько бы цветов в видимой части спектра мы ни брали, нам никогда не удастся покрыть всю область видимых человеком цветов — она ведь не является многоугольником. А чтобы получить все цвета видимой области в качестве основного, пришлось бы выбрать хотя бы один невидимый цвет. Но как же тогда управлять этим невидимым цветом? Возможности человека ограниченны, и это, как обычно, создает ограничения на разработку технологий. Мы же с вами видим, как математика и здесь позволяет объяснить особенности использования информационных технологий.

Вопросы и задания

1. Назовите цвета, которые лежат в основе RGB-кодирования.

2. Рассмотрите еще раз рис. 1.

а) Какой цвет на цветовом кубе соответствует вершине (1; 1; 0)?

б) На этом рисунке координаты одной из вершин цветового куба не указаны. Каковы координаты этой вершины и какому цвету она соответствует?

3. а) Точке с координатами (1/2; 1/2; 0) на цветовом кубе соответствует коричневый цвет. Какой цвет, по вашему мнению, соответствует точке (1/4; 1/4; 0)? А точке (3/4; 3/4; 0)?

б) Какие координаты на цветовом кубе имеет оранжевый цвет?

4. Пусть используется режим True-Color. Укажите цвет, который задается кодом

а) 000000001111111111111111;

б) 011111110111111101111111;

в)* 011111110000000001111111.

5. Пусть используется режим Hi-Color. Укажите цвет, который задается кодом

а) 1111100000011111;

б) 0111101111101111;

в)* 1111101111100000.

6. Сформулируйте законы восприятия цвета, благодаря которым возможна дискретизация цвета при его кодировании. Почему трехбайтового кодирования оказывается достаточно для полноценного цветовоспроизведения?

7. а) Вы хотите работать с разрешением 800 х 600, используя одновременно 65 536 цветов (16-битное кодирование). В магазине продаются видеокарты с памятью 256 Кб, 512 Кб, 1 Мб, 2 Мб, 4 Мб. Какие карты годятся для вашей работы?

б) А если вам необходимо разрешение 1600 х 1200 пикселей и работа с 16 777 216 цветами (24-битное кодирование), какие тогда видеокарты годятся для вашей работы?

в) Подсчитайте объем памяти, необходимой для непосредственной записи 1 секунды видеофильма (25 кадров с разрешением 1024 х 768) при использовании режима True-Color.

8. Объясните, почему добавление видимых цветов в цветовую модель не может обеспечить воспроизведение всех цветов, воспринимаемых человеком.

§ 2. Цветовая модель HSB

Попросите любого художника назвать оттенки красного цвета и услышите, вероятнее всего, следующее: красный, темно-красный, алый, розовый, бледно-розовый и т.п. А еще, говоря о цвете, обычно отмечают его яркость, насыщенность. Эти характеристики цвета в отличие от RGB-модели передают именно субъективное восприятие цвета человеком. Но чтобы с этими характеристиками можно было работать на компьютере, их надо формализовать и описать числовыми параметрами.

С физической точки зрения яркость — это количественная мера световой энергии, излучаемой или отражаемой в сторону наблюдателя. Так, при солнечном свете и в сумерках один и тот же цвет выглядит по-разному, хотя цветовой оттенок один и тот же. Можно сказать, что яркость определяется тем, сколько серого цвета добавлено к основному цвету.

Насыщенность цвета характеризует степень его разбавления белым цветом. Чем больше белого цвета вы добавите, тем меньше насыщенность.

Что касается цветового оттенка, то он определяется расположением цвета в световом спектре. Как вы знаете из физики, видимые человеком цвета располагаются в спектре следующим образом: красный — оранжевый — желтый — зеленый — голубой — синий — фиолетовый. Нередко их располагают по кругу (см. рис. 3), который называют кругом Манселла.

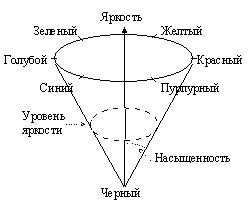
Рис. 3. Круговое расположение цветов

Тогда цветовой оттенок кодируется либо числом, либо длиной дуги, считая, что длина всей окружности равна 1. При этом 0° или дуга нулевой длины соответствуют красному цвету.

Чтобы описать две другие характеристики, используют пространственное изображение этой модели в виде конуса (рис. 4). Угол между осью конуса и образующей характеризует насыщенность цвета, а удаленность от вершины — яркость.

Таким образом, и в этой модели цветопередача характеризуется тремя числами. Сама модель получила название HSB — по первым буквам слов Hue (цветовой оттенок), Saturation (насыщенность) и Brightness (яркость).

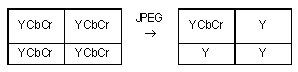
Рис. 4. Цветовая модель HSB

Вопросы и задания

1. Какие факторы принимаются как существенные при построении RGB-модели цветопередачи и какие при построении HSB-модели?

2. Какими характеристиками цвета оперирует HSB-модель цветопередачи?

3. Как кодируется цветовой оттенок в HSB-модели?

4. Укажите, где на цветовом круге располагаются коричневый, оранжевый и фиолетовый цвета. Какими числами, на ваш взгляд, эти цвета кодируются?

§ 3. Необратимые алгоритмы сжатия информации

Алгоритмы сжатия данных, рассмотренные в лекции 1 (“Информатика” № 17/2007), обладали важным свойством — они сжимали данные так, что после декодирования исходное сообщение восстанавливалось в первоначальном виде. Такие алгоритмы называют обратимыми, или алгоритмами сжатия без потери информации. Однако такое буквальное воспроизведение исходной информации важно, как правило, лишь для текстовых сообщений. Если же речь идет о звуковой или видеоинформации, то при разработке алгоритмов сжатия можно учесть особенности человеческого восприятия звука и изображения.

Рассмотрим сначала методы сжатия графических данных. Одним из наиболее применяемых методов и фактически признанным сегодня стандартом сжатия является алгоритм, созданный Группой экспертов по фотоизображениям. Он получил название JPEG по первым буквам английского названия этой организации: Joint Photographic Experts Group.

Алгоритм JPEG основан на учете целого ряда особенностей зрительного аппарата человека. Во-первых, как мы уже рассказывали в учебнике 10-го класса, человеческое зрение обладает некоторой инерцией, т.е. изображение исчезает не мгновенно, а на некоторое время сохраняется. Именно этот эффект привел в свое время к созданию кинематографа. Именно этот эффект позволяет осуществлять дискретизацию изображения с последующей его оцифровкой. Во-вторых, чувствительность человеческого глаза к зеленому цвету почти в 4 раза выше, чем к красному, и почти в 10 раз выше, чем к синему. Значит, и для передачи информации о красной и синей составляющих можно использовать меньший объем памяти.

Само сжатие осуществляется алгоритмом JPEG в несколько этапов. Прежде всего производится перекодировка из RGB-модели в так называемую “YCbCr-модель”. В этой модели цвет представлен характеристиками: Y — яркость зеленого цвета, Cb — “цветоразность” зеленый–синий, Cr — “цветоразность” зеленый–красный (мы не даем точного определения понятию “цветоразность”, поскольку не планируем абсолютно точно описывать алгоритм JPEG, а интуитивное понимание этого слова есть, как мы надеемся, у каждого читателя). Затем в каждом втором столбце и в каждой второй строке таблицы пикселей, заполняющих экран, информация о Cb и Cr стирается. Иными словами, для каждого квадратика из четырех пикселей только в одном остается информация о цветоразностях (см. рис. 5).

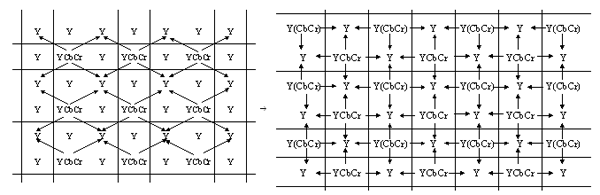
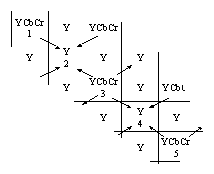
Рис. 5. Сжатие по алгоритму JPEG

Это преобразование уменьшает объем данных в два раза: на каждые 4 пикселя вместо 12 значений передается только 6. После этого получившиеся числовые данные сжимаются еще и алгоритмом Хаффмана.

При декодировании непередаваемые характеристики цвета восстанавливаются так, чтобы у зрителя создавалось ощущение непрерывного изменения цвета. На рис. 6 схематично показано, информация о каких пикселях определяет значение непередаваемых характеристик при декодировании. Сначала приближенно восстанавливаются значения для пикселей, расположенных по диагонали от пикселей с полной цветовой информацией, а затем значения для остальных пикселей.

Рис.6. Схема восстановления характристик при декодировании

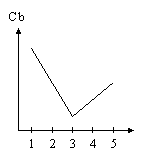
Рис. 7. График значений характеристики Cb вдоль ряда 1-2-3-4-5

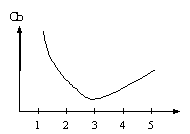
Рис. 8. Сглаживание функции

Самый простой способ определения непередаваемых характеристик — вычисление среднего арифметического четырех известных значений. Однако если изобразить график изменения какой-либо восстанавливаемой характеристики (например, Cb) вдоль ряда пикселей с номерами 1, 2, 3, 4, 5, то вполне вероятно, что он в этом случае будет выглядеть так, как показано на рис. 7. Резкая смена направления в точке 3 изменения значений характеристики Cb вряд ли имела место в оригинале изображения. Математиками разработаны специальные методы, позволяющие, как говорят, сглаживать такие переходы (см. рис. 8). На математическом языке это означает, что функция, описывающая значения характеристики, не только непрерывна, но и дифференцируема, т.е. в каждой точке имеет производную. Для построения такой функции учитываются значения не только в четырех ближайших точках, но на гораздо более обширной области, а иногда и на всем множестве точек с известными значениями функции.

Впрочем, попытка учесть как можно больше точек вовсе не всегда эффективна. Такие функции получаются слишком громоздкими и сложными для вычислений. Математиками разработана теория так называемых “сплайнов”, которые позволяют гладко “склеивать” функции, определенные на небольшом множестве точек и легко вычисляемых.

Стандартизацией алгоритмов сжатия видеоданных занимается Группа экспертов по видеоизображениям — Motion Picture Experts Group. Поэтому алгоритмы, удовлетворяющие стандартам, принятым этой группой, принято называть общим именем MPEG. Среди них и алгоритм MPEG-1 Layer 3, более известный по своему сокращенному названию МР3. На самом деле этот алгоритм предназначен для сжатия аудиоинформации. Одним из параметров, регулирующих степень сжатия, является так называемый битрейт (от англ. bitrate) — количество бит, используемых для кодирования одной секунды звука.

Звук, как известно, — это колебательный процесс. Математики научились любое сложное колебание представлять в виде суммы простых колебаний, каждое из которых описывается амплитудой, частотой и фазой. Оказывается, что некоторыми составляющими можно просто пренебречь — даже самый музыкальный слух не уловит их отсутствие. Ответственность за то, какие составляющие и в каком количестве оставить, как раз и несет битрейт. Но даже при самом большом допустимом битрейте стандарта МР3 — 320 Кбит/с — данный алгоритм обеспечивает четырехкратное сжатие информации по сравнению с форматом Audio CD при том же субъективном восприятии качества звука. На заключительном этапе к полученным данным снова применяется алгоритм Хаффмана.

Алгоритмы сжатия собственно видеоинформации используют самые разнообразные подходы. Одним из базовых является метод опорного кадра. Дело в том, что при переходе от одного кадра к следующему нередко большая часть изображения остается неизменной. Если, к примеру, происходит встреча героев фильма в некоторой комнате, то ее обстановка, занимающая основную часть кадра, останется той же самой. Поэтому можно сохранять не целиком следующий кадр, а только изменения по сравнению с предыдущим кадром.

С другой стороны, если в кадре есть быстро сменяемые участки, то их можно кодировать с более низким качеством — человек привык к тому, что он не может рассмотреть детали быстро изменяющихся объектов. При этом статичное изображение и динамично меняющееся изображение можно отделить друг от друга и применять к ним разные алгоритмы сжатия. И только после декодирования их снова соединить в одно изображение.

Назовем имена нескольких алгоритмов из семейства MPEG.

MPEG-1 использовался в первых Video CD (VCD-I).

MPEG-2 используется в DVD и Super Video CD (SVCD, VCD-II).

MJPEG — формат сжатия видеоизображений, в котором каждый кадр сжимается по алгоритму JPEG.

MPEG-4 — один из самых эффективных форматов сжатия видео.

DivX, XviD — улучшенные модификации формата MPEG-4.

Вопросы и задания

1. Какой алгоритм сжатия данных называется обратимым?

2. В чем состоит отличие обратимых алгоритмов сжатия от необратимых?

3. Какие особенности человеческого зрения позволяют применять необратимые алгоритмы сжатия графических изображений без потери качества?

4. Пусть V₀ — исходный объем данных, V — объем данных после обработки их сжимающим алгоритмом. Как, на ваш взгляд, обычно меняется отношение V₀ / V при увеличении V₀: возрастает, убывает или остается примерно одним и тем же?

* Возможно, читателю будет небезынтересно узнать, что весь материал, изложенный как в лекциях Педагогического университета, так и в данных публикациях, представляет собой двухгодичный факультативный курс “Математические основы информатики”, читаемый автором данных публикаций и его коллегами в 10–11-х классах информационно-математического профиля, открытых в Лицее при Уральском государственном университете им. А.М. Горького. Поэтому мы приводим в конце каждого параграфа комплект заданий, которые предлагаются учащимся этих классов, — если кто-то из читателей захочет, следуя предложенным материалам, создать, например, элективный курс, они, мы надеемся, ему в этом помогут.