"Математические построения и программирование"

Недавно надо было нам найти телефон достаточно известной компьютерной фирмы. И как назло "Интернет сломался". Минут 30 мучили мы новый толстый и глянцевый справочник "Желтые страницы", нашли наконец... Какую-то бабушку потревожили, телефон неверным оказался. В нашем книжном шкафу немало книг, страницы которых давно пожелтели от времени. Но это совсем другие желтые страницы...

Имя Сергея Александровича Абрамова учителям информатики со стажем хорошо известно прежде всего благодаря знаменитому "зеленому задачнику"¹ (на протяжении нескольких лет мы печатали решения задач из него). Значительным событием было также появление книги "Основы информатики"², которая широко использовалась в качестве учебника в классах с углубленным изучением математики и информатики. В библиотечках московских учителей имеются и другие методические пособия, написанные под руководством Сергея Александровича (они издавались тиражами меньшими, чем две ранее упомянутые книги, и печатались в типографии ВЦ РАН). Книга "Математические построения и программирование" менее известна, поскольку вышла достаточно давно —в 1978 году. Однако именно на нее мы хотим обратить внимание наших читателей. Эта ничуть не потерявшая актуальности книга по праву занимает свое место в ряду бесценных работ А.Л. Брудно, Д.Кнута, А.Г. Кушниренко, А.Х. Шеня и других известных авторов.

В одном из последних номеров в рубрике "Книжный шкаф учителя информатики" мы рассказали о замечательной книге Джорджа Пойа "Математическое открытие". Изданные примерно в одно время книги Пойа и Абрамова объединяют глубина и тщательная методическая проработка всех вопросов, основанные на многолетнем преподавательском опыте авторов. При этом, разумеется, информатикам книга Абрамова более близка и понятна, поскольку речь в ней идет исключительно о вопросах алгоритмизации и программирования. По уже сложившейся традиции в материалах этой рубрики мы стараемся предоставить слово авторам рассматриваемых книг. Ниже приводится фрагмент из авторского предисловия к "Математическим построениям...".

"Эта книга — не учебник программирования. Здесь совершенно отсутствуют как сведения о современных вычислительных машинах, так и инструкции по составлению программ для этих машин. Предмет книги — разнообразные темы, обсуждение которых будет способствовать развитию алгоритмической интуиции читателей и даст представление о характерных приемах решения алгоритмических задач".

В книге затрагиваются различные вопросы алгоритмизации и рассматриваются некоторые классические алгоритмы. Оглавление книги дает достаточно полное представление о ее содержании.

Глава I. Построения и алгоритмы

§ 1. Примеры задач на построение. Данные, операции
§ 2. Логический анализ ситуации
§ 3. Запись алгоритмов, которые содержат проверки
§ 4. Различные наборы операций
§ 5. Избыточность набора операций

Глава II. Цикл

§ 1. Ограниченность поля зрения
§ 2. Логические выражения
§ 3. Повторение действий
§ 4. Массивы
§ 5. Алгоритм Евклида

Глава III. Рекурсия

§ 1. Упрощение исходных данных
§ 2. Рекуррентные соотношения
§ 3. Анализ рекурсивных алгоритмов
§ 4. Как выполнять рекурсивные алгоритмы
§ 5. Пример избавления от рекурсии

Глава IV. Поиск

§ 1. Справочник и поиск сведений в нем
§ 2. Подмножества конечных множеств
§ 3. Бектрекинг
§4. Восемь ферзей и лабиринт
§ 5. Графы и деревья

Глава V. Дальнейшие рассмотрения

§ 1. Подстановки
§ 2. Вычисление а^п
§ 3. Алгоритмы с логарифмической трудоемкостью

Дополнение I. Переходы

Дополнение II. Об одном полезном качестве рекурсии

Следует отметить, что, помимо задач, на которых рассматриваются основные вопросы, практически все параграфы книги содержат множество дополнительных упражнений, задач и задачек, вопросов для размышления и этюдов для исследований. Вот пример такой задачки из четвертого параграфа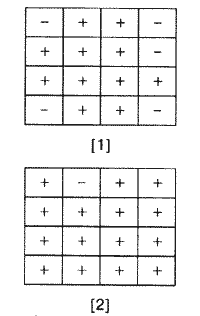 первой главы.

"Рассмотрим следующий пример. Даны две таблицы 4x4, заполненные знаками "+" и "-" (см. рисунок). Разрешается производить следующие операции:

1) заменить в некоторой строке каждый "+" на "-" и наоборот;

2) заменить в некотором столбце каждый "+" на "-" и наоборот.

Существует ли последовательность данных операций, переводящая таблицу [1] в таблицу [2]?"

Попробуйте решить эту задачку. Более двадцати лет назад старшеклассникам она не казалась сложной.

¹Абрамов СЛ. и др. Задачи по программированию. М., Наука, 1988.

²Абрамов СА., Зима Е.В. Основы информатики. М., Наука, 1989.