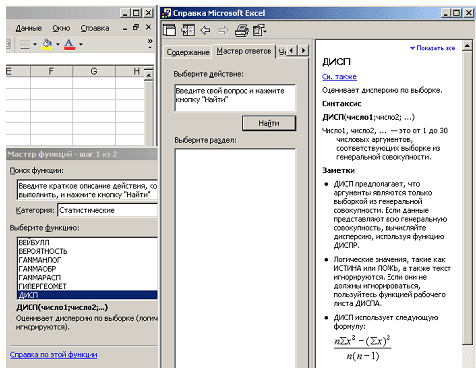
Профильная школа. ЭкзаменыПримерные ответы на профильные билетыТ.Н. Катанова,г. Пермь Продолжение. Начало см. в № 19–24/2006, 1, 4–9/2007 Билет № 231. Математическая обработка статистических данных, результатов эксперимента. Использование динамических (электронных) таблиц для выполнения учебных заданий из различных предметных областей: обработка результатов естественно-научного и математического эксперимента, экономических и экологических наблюдений, социальных опросов, задач по учету и планированию, учета индивидуальных показателей учебной деятельности.В настоящее время все математические пакеты позволяют автоматизировать процесс обработки статистических данных, результатов эксперимента. Наиболее простым средством такого рода обработки является табличный процессор (электронная таблица). В MS Excel в наборе доступных функций (математических, логических и т.д.) в категории “Статистические” содержится несколько десятков функций, позволяющих проводить разного рода статистическую обработку. На рисунке справа представлена справка (а ее можно получить по любой функции), коротко описывающая, что такое дисперсия и каким образом ее можно оценить средствами Excel.
Приведем несколько примеров статистической обработки данных. Пример 1. Предположим, что из инструментов, отштампованных одной и той же машиной, выбираются наугад 10 штук и испытываются на излом. Вычислим дисперсию для некоторой выборки (задана прилагаемая к инструментам сила).
Функция ДИСП использует следующую
формулу: . Для нашей выборки получаем результат 434,6778. Пример 2. Для выборки из примера 1 подсчитаем сумму квадратов отклонений от среднего значения. Воспользовавшись функцией КВАДРОТКЛ, получаем результат 3912,1. Пример 3. Установим, есть ли какая-либо взаимосвязь между двумя последовательностями данных.
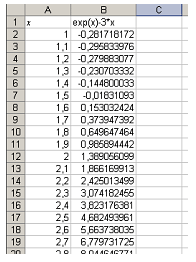
Для ответа на сформулированный вопрос необходимо вычислить коэффициент корреляции. Коэффициент корреляции используется для определения наличия взаимосвязи между двумя свойствами. Например, можно установить зависимость между средней температурой в помещении и использованием кондиционера. Для этих целей воспользуемся функцией КОРРЕЛ. Получаем для наших данных 0,598841746. 2. Написать и отладить программу обработки вещественных данных.Пример. Написать и отладить программу приближенного нахождения корня уравнения ex - 3x =0 на отрезке [1; 5] методом половинного деления с точностью 0,01. Решение. Решение задачи состоит из двух частей — отделение корня и уточнение корня. Отделение корня можно реализовать программно или с помощью вспомогательных программных средств (например, с помощью MS Excel). Рассмотрим второй вариант отделения корня (напомним, что на некотором отрезке существует корень, если функция на этом отрезке меняет знак; если она к тому же монотонна, то корень единственный). Протабулируем левую часть уравнения на заданном отрезке с шагом 0,1.
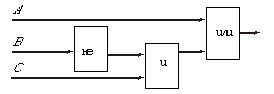
Замечаем, что рассматриваемая функция на заданном отрезке [1; 5] меняет знак лишь единожды на отрезке [1,5; 1,6]. На этом отрезке и будем уточнять корень. QBasicDECLARE FUNCTION F! (x!) PRINT "Введите a, b, eps:" INPUT a, b, eps DO c = (a + b) / 2 IF F(a) * F(c) < 0 THEN b = c ELSE a = c LOOP UNTIL b — a < eps x = (a + b) / 2 PRINT USING "###.######"; x FUNCTION F (x) F = EXP(x) — 3 * x END FUNCTION Pascalprogram divide_half; var a,b,c,eps,x:real; function f(x:real):real; begin f := exp(x) - 3*x end; begin write('Введите a, b, eps: '); readln(a, b, eps); repeat c := (a + b)/2; if f(a) * f(c) < 0 then b := c else a := c until b – a < eps; x := (a + b)/2; writeln('x=', x:10:7) end. C++#include <iostream.h> #include <math.h> double f(double x); void main() { double a,b,c,eps,x; cout << "Введите a, b, eps:"; cin >> a >> b >> eps; do { c = (a + b)/2; if (f(a) * f(c) < 0) b = c; else a = c; } while (b – a >= eps); x = (a + b)/2; cout << x; } double f(double x) { return exp(x) – 3 * x; } ЗаданияНа отрезке [–10; 10] (или на той его части, что входит в область определения уравнения) отделите корни. Уточните один из корней по методу половинного деления с точностью e с помощью программы для компьютера. Уравнения: 1) x – 10sinx = 0 Контроль 1-й корень [-8.43;-8.42] x = -8.42320393239788 2-й корень [-7.07;-7.06] x = -7.06817435807170 3-й корень [-2.86;-2.85] x = -2.85234189447510 4-й корень [-0.01; 0.00] x = 0.00000000002053 5-й корень [ 2.85; 2.86] x = 2.85234189443872 6-й корень [ 7.06; 7.07] x = 7.06817435810808 7-й корень [ 8.42; 8.43] x = 8.42320393235423 2) xsinx – 1 = 0 Контроль (для отрезка [–10; 10]) 1-й корень [-9.32;-9.31] x = -9.31724294142623 2-й корень [-6.44;-6.43] x = -6.43911723842757 3-й корень [-2.78;-2.77] x = -2.77260470826150 4-й корень [-1.12;-1.11] x = -1.11415714090799 5-й корень [ 1.11; 1.12] x = 1.11415714084615 6-й корень [ 2.77; 2.78] x = 2.77260470827241 7-й корень [ 6.43; 6.44] x = 6.43911723843485 8-й корень [ 9.31; 9.32] x = 9.31724294144078 3) 2x2 – 5 = 2x Контроль 1-й корень [-1.64;-1.63] x = -1.63137672535049 2-й корень [ 2.18; 2.19] x = 2.18478845171194 3-й корень [ 6.13; 6.14] x = 6.13493835514964 4) 4x4 – 6,2 = cos0,6x Контроль 1-й корень [-1.15;-1.14] x = -1.14899614950809 2-й корень [ 1.14; 1.15] x = 1.14899614952083 5) ln(x + 6,10 = 2sin(x – 1,4) Контроль 1-й корень [-5.93;-5.92] x = -5.92148540437483 2-й корень [-4.73;-4.72] x = -4.72227504245529 3-й корень [-2.45;-2.44] x = -2.44636594824988 6) 2-x = 1 – 0,5x2 Контроль 1-й корень [-2.69;-2.68] x = -2.68003383521864 2-й корень [ 4.46; 4.47] x = 4.46197840075183 7) 5sin2x = sgrt(1-x) Контроль 1-й корень [-18.32;-18.31] x = -18.31275351383374 2-й корень [-17.81;-17.80] x = -17.80359794106334 3-й корень [-15.24;-15.23] x = -15.23931500948675 4-й корень [-14.60;-14.59] x = -14.59236215599230 5-й корень [-12.17;-12.16] x = -12.16045625391416 6-й корень [-11.39;-11.38] x = -11.38599320170761 7-й корень [-9.09;-9.08] x = -9.08077073001186 8-й корень [-8.18;-8.17] x = -8.17946302043856 9-й корень [-6.01;-6.00] x = -6.00429034909757 10-й корень [-4.97;-4.96] x = -4.96761637068994 11-й корень [-2.94;-2.93] x = -2.93754330773299 12-й корень [-1.74;-1.73] x = -1.73949286292191 13-й корень [ 0.09; 0.10] x = 0.09567866423583 3. Построить таблицу истинности для заданной логической схемы (логическая схема должна содержать не менее трех входов).Пример Построить таблицу истинности для данной логической схемы:
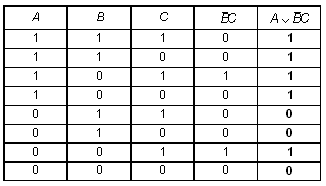
Решение
Таблица истинности построена так. По заданной схеме записано соответствующее ей логическое выражение. Получаем Строим соответствующую ему таблицу истинности. Примечание. В действительности логические элементы обозначаются не так, как в приведенном примере; их обозначения приведены в билете № 9. В заданиях ниже используются именно такие обозначения. Задания Построить таблицу истинности для данных логических схем.
Литература 1. Введение в информатику. Лабораторные работы. / Авт.-сост. А.П. Шестаков; Пермский университет. Пермь, 1999, ч. I, 56 с. |