ЭНЦИКЛОПЕДИЯ УЧИТЕЛЯ ИНФОРМАТИКИ. Выпуск 5

Окончание. Начало см. в № 14/2007

Оператор — это элемент языка, задающий полное описание действия, которое необходимо выполнить. Каждый оператор представляет собой законченную фразу языка программирования и определяет некоторый вполне законченный этап обработки данных. В состав операторов могут входить служебные слова, данные, выражения и другие операторы. В английском языке данное понятие обозначается словом “statement”, означающим также “предложение”.

Каждый оператор в любом языке программирования имеет определенный синтаксис и семантику. Под синтаксисом оператора понимается система правил (грамматика), определяющая его запись с помощью элементов алфавита данного языка, в который наряду с различными символами входят, например, и служебные слова. Под семантикой оператора понимают его смысл, т.е. те действия, которым соответствует запись того или иного оператора. Например, запись i := i + 1 является примером синтаксически корректной записи оператора присваивания в языке Pascal, семантика которого в данном случае такова: извлечь значение ячейки памяти, соответствующей переменной i, сложить его с единицей, результат записать в ту же ячейку памяти.

В большинстве процедурных языков программирования набор операторов практически одинаков и состоит из оператора присваивания, операторов выбора, операторов цикла, оператора вызова процедуры, операторов перехода. Иногда выделяют также пустой (отсутствие действия) и составной операторы. Многие операторы являются способом представления определенных алгоритмических конструкций (см. “Алгоритмические конструкции” ) в языке программирования. Рассмотрим группы операторов подробнее, используя синтаксис языка Pascal.

Оператор присваивания

Присваивание — это действие компьютера, в результате которого переменная получает значение вычисленного выражения (оно помещается в соответствующую переменной ячейку памяти). Для описания такого действия в языках программирования существует оператор присваивания.

В общем виде оператор присваивания записывается так:

<переменная> <знак присваивания> <выражение>

Например, в языке Pascal в качестве знака присваивания используется комбинация символов :=. В ряде других языков — знак равенства.

Результатом выполнения оператора присваивания является изменение состояния данных: все переменные, отличные от переменной, стоящей в левой части оператора присваивания, не меняют своего значения, а указанная переменная получает значение выражения, стоящего в правой части оператора присваивания. В большинстве случаев требуется, чтобы тип выражения совпадал с типом переменной. Если это не так, то оператор либо считается синтаксически некорректным, либо производится преобразование типа выражения к типу переменной (см. 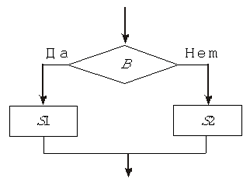“Типы данных” ).

Операторы выбора

По-другому эти операторы называют условными операторами. Условные операторы используются для программирования алгоритмов, содержащих алгоритмическую конструкцию ветвление.

В языках программирования имеется несколько видов условных операторов. Полный условный оператор соответствует алгоритмической структуре полного ветвления:

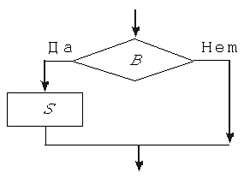
В языке программирования соответствующий условный оператор имеет вид:

if B then S1 else S2

Если выражение B, которое вычисляется в начале выполнения условного оператора, имеет значение “истина”, то будет выполняться оператор S1, в противном случае — оператор S2. Операторы S1 и S2 могут быть составными.

Алгоритмическая структура неполного ветвления реализуется с помощью неполного условного оператора, который имеет вид:

if B then S

Здесь B — логическое выражение, а S — произвольный оператор. Оператор S будет выполняться, если выражение B окажется истинным.

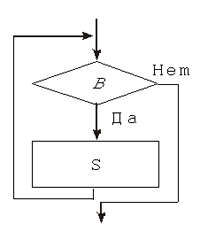
Если условный оператор реализует всего две ветви выбора (“да” и “нет”), то с помощью оператора варианта (case-оператора) можно запрограммировать многоветвящуюся структуру. Оператор варианта имеет вид:

case E of

V1: S1;

…

Vn: Sn;

end

Выполняется данный оператор так: значение выражения E ищется среди перечисленных в записи оператора значений V1, V2, …, Vn, и если такое значение находится, то выполняется соответствующий оператор S1, S2, …, Sn.

В разных языках программирования синтаксис и даже семантика перечисленных операторов могут отличаться, но возможности, предоставляемые программисту подобными конструкциями, примерно одинаковы.

Пример 1. В статье “Алгоритмические конструкции” 2 был приведен пример записи алгоритма решения обобщенного квадратного уравнения с помощью конструкций ветвления. Приведем фрагмент программы на языке Pascal, реализующий этот же алгоритм:

readln(a,b,c);

if a = 0 then

   if b = 0 then

      if c = 0 then writeln('x — любое')

      else writeln('нет корней')

   else writeln(—c/b)

D := b*b — 4*a*c;

   if D < 0 then writeln('нет корней')

   else begin

      x1 := -b + sqrt(D);

      x2 := -b - sqrt(D);

      writeln(x1:0:2,''', x2:0:2)

   end

end;

Операторы цикла реализуют циклические алгоритмические конструкции, они используются для действий, повторяющихся многократно. Во многих языках программирования существуют три вида операторов цикла: “c предусловием”, “c постусловием”, “с параметром”.

Необходимой и достаточной алгоритмической структурой для программирования циклов является цикл “с предусловием”, поэтому его можно назвать основным типом цикла. Оператор цикла с предусловием имеет вид:

while B do S

Оператор S, для многократного выполнения которого создается цикл, называется телом цикла. Выполнение оператора цикла сводится к повторному выполнению тела цикла, пока значение логического выражения B истинно (до тех пор, пока оно не станет ложным). Фактически подобные операторы цикла реализуют повторное выполнение условных операторов if B then S, пока истинно условие B.

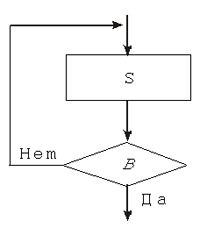
Пример 2. Рассмотрим применение такого оператора цикла для подсчета суммы цифр натурального числа N:

S := 0;

while N > 0 do begin

S := S + N mod 10;

N := N div 10

end;

writeln(S);

В цикле с постусловием тело цикла предшествует условию В. В отличие от цикла с предусловием здесь В — это условие окончания цикла. Оператор цикла с постусловием в Паскале имеет вид:

repeat S until B

При такой организации цикла тело цикла S хотя бы один раз обязательно выполнится.

Практически во всех процедурных языках существует оператор цикла c параметром. Схематично его можно представить так:

for <переменная> E1 to E2 step E3 do S

Здесь значение переменной (параметра цикла) меняется от значения выражения E1 до E2 с шагом E3. Для каждого такого значения параметра цикла выполняется оператор S. В языке Pascal понятие шага в описании этого оператора отсутствует, а сам шаг для целочисленного параметра цикла может быть равен либо 1, либо –1. Оператор “цикл с параметром” используется для программирования циклов с заданным числом повторений. Для программирования итерационных циклов (число повторений которых заранее неизвестно) он не годится.

Оператор вызова процедуры

В статье “Подпрограммы” 2 подробно рассказывается о таком виде подпрограмм, как процедуры. Стандартные подпрограммы языка программирования, которые входят в одну из библиотек подпрограмм, а также пользовательские подпрограммы, описанные внутри данного блока, вызываются с помощью оператора вызова процедуры:

<имя процедуры>(E1,E2,…,En)

Здесь E1,E2,…,En — переменные или выражения, представляющие собой фактические параметры обращения к процедуре. Наиболее часто используемыми стандартными процедурами являются процедуры ввода и вывода данных (read и write в Pascal).

Вызов процедуры семантически эквивалентен выполнению блока, описанного в качестве тела процедуры, после передачи в него начальных значений некоторых переменных (параметров-значений) или замены имен некоторых переменных (параметров-переменных) на имена фактических переменных, указанных при вызове процедуры.

Пример 3. Пусть у нас описана процедура abc:

procedure abc(a,b:integer;var c: integer);

c := a + b

end;

Вызов этой процедуры abc(2,3,x) эквивалентен блоку действий:

a := 2;

b := 3;

x := a + b;

Операторы перехода

Наиболее известным в данной группе операторов является оператор безусловного перехода goto. Если ко всем или некоторым уже имеющимся операторам программы добавить метки, то в программе становится возможным использовать оператор перехода вида:

goto <метка>

Метка в данном случае соответствует началу того оператора, с которого должно продолжиться выполнение программы. Такой оператор позволяет записывать в языке программирования алгоритмы, имеющие сколь угодно сложную структуру. Но зачастую использование безусловного перехода неоправданно, т.к. ведет к запутанной, плохо читаемой программе. Практически единственным осмысленным применением оператора goto является выход сразу из нескольких вложенных циклов, например, при обработке двухмерных массивов.

Пример 4. Пусть нам требуется определить, есть ли в двухмерном массиве a элемент, равный 0:

b := false;

for i := 1 to N do

for j := 1 to N do

if a[i,j] = 0 then begin

b := true;

goto 1

end;

1: if b then write('есть') else write('нет');

Программа, разработанная по правилам структурного программирования, не должна содержать операторов безусловного перехода. Приведенную выше программу без использования оператора goto можно переписать следующим образом:

b := false;

i := 0;

while not b and (i < N) do begin

i := i + 1

j := 0;

while not b and (j < N) do begin

j := j + 1

if a[i,j] = 0 then b := true;

end;

end;

if b then write('есть') else write('нет');

В данном случае структурная программа менее наглядна, чем программа с goto.

В языках программирования могут быть определены и другие операторы перехода. Например, в языке Pascal: break (досрочное прерывание цикла, переход на оператор, который должен выполняться после завершения цикла), continue (досрочное завершение текущей итерации цикла и переход к следующей), exit (досрочное прерывание подпрограммы, выход из нее), halt (досрочное прерывание программы, переход на ее конец). Аналогичные операторы существуют и в языках С, С++, Java.

Составной оператор — это группа операторов, заключенных в операторные скобки (в Pascal — begin … end; в C, C++ — {…}).

Составной оператор введен в языки программирования для облегчения описания конструкций языка. Так, например, в Pascal исполняемая часть каждого блока (программа, процедура, функция) представляет собой один составной оператор. Ровно так же тело любого оператора цикла состоит только из одного оператора, быть может, составного. Альтернативой составному оператору может быть служебное слово, обозначающее окончание того или иного оператора, например, END IF в языке Basic.

Методические рекомендации

Тема “Операторы языка программирования” обычно изучается только в контексте рассмотрения определенного языка программирования. При ее рассмотрении важно показать связь базовых алгоритмических конструкций и операторов: алгоритмические конструкции записываются в языке программирования с помощью соответствующих операторов. Исключение в некотором смысле составляет последовательная конструкция, она определяет линейный порядок выполнения действий. Действия в строго линейной программе реализуются только операторами присваивания и операторами вызова процедуры.

На начальном этапе обучения программированию у школьников возникает много проблем. Первый психологический барьер им приходится преодолевать при изучении оператора присваивания. Одна из основных задач, которую необходимо решить вместе с учениками, это обмен местами значений двух переменных. Можно предложить школьникам мысленно решить задачу, как поменять местами содержимое двух ящиков, например, письменного стола. Обычно на данном этапе обсуждения ученики догадываются, что для решения задачи необходим третий ящик (переменная). Тем не менее при записи данного алгоритма они часто путают, в какой части оператора присваивания (левой или правой) должна стоять та или иная переменная.

Ошибки в записи арифметических и логических выражений возникают из-за незнания старшинства операций, которые используются в выражении. При этом под операциями понимаются не только арифметические, но и операции сравнения и логические связки, а в языке С и операция присваивания, что весьма непривычно для школьников. Ситуация осложняется тем, что в разных языках программирования одни и те же операции имеют разные относительные приоритеты. Обращать внимание следует и на соответствие типов переменной и выражения в левой и правой частях оператора присваивания (см. “Типы данных”).

При освоении операторов выбора полезно предложить школьникам запрограммировать алгоритм, содержащий многоветвящуюся структуру, как с помощью комбинации условных операторов, так и с помощью оператора выбора.

Пример. В целочисленную переменную N вводится возраст человека в годах. Напечатать фразу “Мне K лет”, заменяя слово лет на год или года в зависимости от числа K. Приведем два решения этой задачи:

var k: integer;

begin

readln(k);

if (k mod 100) in [11..20]

then writeln('Мне ',k,' лет')

else

case k mod 10 of

0,5..9:writeln('Мне ',k,' лет');

1:writeln('Мне ',k,' год');

2..4:writeln('Мне ',k,' года');

end

var k, n: integer;

begin

readln(k); n := k mod 10;

if (k mod 100) in [11..20]

then writeln('Мне ',k,' лет') else

if n = 1 then writeln('Мне ',k,' год')

else

if (n >=) and (n <= 4)

then writeln('Мне ',k,' года')

else writeln('Мне ',k,' лет')

end.

При рассмотрении операторов цикла полезно предложить одну и ту же задачу запрограммировать тремя разными способами с использованием трех операторов цикла, и наоборот, по условию задачи научиться определять, какой именно оператор цикла является наиболее подходящим в том или ином случае.

Оператор вызова процедуры только на первый взгляд является простым. Здесь важно объяснить правила передачи параметров в процедуры и функции, различие между параметрами-переменными и параметрами-значениями (в последнем случае мы можем передавать не только имя переменной, но и константу или даже выражение соответствующего типа). Формальные и фактические параметры должны соответствовать по типам, но не по именам, что является далеко не очевидным для учеников.

Изучение условного и особенно составного оператора — хороший повод поговорить с учениками о стиле написания программ. Для языка Pascal существует несколько распространенных способов записи структурированных программ, но все они содержат отступы для размещения вложенных структур. Важны для записи программ и комментарии.

Массив — это последовательность однотипных элементов, число которых фиксированно и которым присвоено одно имя. В языках программирования массивы используются для реализации таких структур данных, как последовательности и таблицы (см. статьи “Структуры данных”, “Типы данных”). Положение элемента в массиве однозначно определяется его индексом — номером элемента в последовательности (например, a₁, a₂, a₃, ..., a_n), номером строки и столбца в таблице (a_{1 1}, a_{2 5}, ..., a_{n n}) и т.д.

Заполнение массива элементами псевдослучайной последовательности

Заполнять массив можно либо считывая значение каждого элемента, либо присваивая элементам некоторые значения. Вводить значения элементов с клавиатуры не всегда удобно. Более того, часто при отладке программы нам надо сделать так, чтобы она работала на произвольных массивах. В этом случае очень удобно задавать значения элементов массива случайным образом, с использованием встроенного в язык программирования так называемого датчика псевдослучайных чисел. Числа называются псевдослучайными, так как для их нахождения используется некая итерационная последовательность r_i = f(r_i-1), например, r_i = (ar_i-1 + b) mod c, здесь mod — операция взятия остатка от деления на c; a, b, c — некоторые константы. Любая подобная последовательность имеет периодические свойства (т.е., начиная с какого-то момента, числа начнут повторяться в том же самом порядке).

В языке программирования Pascal псевдослучайная последовательность реализована функцией random. Если использовать ее без параметров, то при очередном обращении она будет выдавать в качестве результата некоторое псевдослучайное вещественное число из диапазона [0; 1), для этого ri делится на c. Процедура randomize предназначена для задания первого значения в последовательности ri. Для этого она использует текущее значение компьютерного таймера; в результате при разных запусках программы последовательности получаются различными. Обращаться к процедуре randomize имеет смысл только один раз — в начале работы программы. Для получения целых случайных чисел из диапазона [0; n–1] используется вызов функции random с параметром n: random(n).

Пример 1. Приведем пример заполнения случайным образом целочисленного массива a, состоящего из n элементов, десятичными цифрами (от 0 до 9 включительно):

randomize;

for i := 1 to N do a[i] := random(10);

Суммирование элементов массива

Одной из распространенных операций с массивами является операция нахождения суммы значений элементов массива. Например, это нужно для нахождения среднего арифметического значения элементов. Приведем основной фрагмент решения этой задачи:

S := 0; {переменная для накопления результата}

for i := 1 to N do

S := S + a[i];

Циклический сдвиг элементов массива

Под циклическим сдвигом элементов массива подразумевается, что все элементы массива сдвигаются на один элемент влево или вправо, а первый (последний) элемент становится последним (первым). Несмотря на кажущуюся простоту, данная задача вызывает затруднения при сдвиге вправо. А такая операция нужна, например, при реализации вставки элемента в массив (часть массива для этого сдвигается вправо). В данном случае операцию сдвига нужно производить с конца массива:

с := a[N]; {запоминаем последний элемент

во вспомогательной переменной}

for i := N downto 2 do

a[i] := a[i - 1];

a[1] := c;

Поиск в массиве

Поиск максимума и минимума

Алгоритм поиска максимального и минимального элементов массива по реализации несколько отличается от аналогичного алгоритма для последовательностей. В массиве правильнее искать не значение максимального или минимального элемента, а индексы соответствующих элементов, тогда автоматически мы будем знать и сами значения. Таким образом, делать двойную работу не нужно (в одной переменной хранить значение максимального элемента, а в другой — ее индекс). Приведем основную часть наиболее экономичного решения задачи обмена местами минимального и максимального элементов массива.

imax := 1; {индекс максимального элемента}

imin := 1; {индекс минимального элемента}

for i := 2 to N do

if a[i] > a[imax] then imax := i else

if a[i] < a[imin] then imin := i;

c := a[imin];

a[imin] := a[imax];

a[imax] := c;

Заметим, что если в массиве несколько элементов, равных максимальному и/или минимальному значению, то данная программа найдет первые вхождения максимума и минимума.

Поиск числа К в массиве

Алгоритм поиска в неупорядоченном массиве, индексы которого меняются от 1 до N, значения, равного K, может выглядеть так:

i := 0;

repeat

i := i + 1

until (i = N) or (a[i] = K);

if a[i] = K then write(i) else write(0)

При отсутствии в массиве элемента с искомым значением K печатается нулевое значение. Оказывается, что и такую программу можно упростить при использовании так называемого “барьерного” метода, который часто применяется в программировании. В данном случае он заключается в том, что мы заносим в дополнительный элемент массива (например, нулевой) искомое значение K и в условии окончания цикла отказываемся от проверки на выход за границу массива:

a[0] := K;

i := N;

while (a[i] <> K) do

i := i — 1;

write(i)

Эта программа не просто проще и эффективней. В ней практически невозможно сделать ошибку. Если значений K среди элементов массива несколько, то найдено будет первое справа.

Поиск числа К в упорядоченном массиве

Рассмотрим массив, элементы которого упорядочены по неубыванию. То есть a₁ a₂ … a_n. Поиск элемента, равного K, в таком массиве осуществляется с помощью алгоритма “деления пополам”. По-другому его еще называют бинарным поиском, или дихотомией. Алгоритм заключается в том, что мы сравниваем средний элемент массива с числом K и, в зависимости от результата сравнения, переходим к поиску K либо в левой, либо в правой частях массива. Далее наши действия повторяются, пока рассматриваемая часть массива не будет состоять из одного элемента. Если он не равен K, то такого значения в массиве нет. Приведем пример эффективной реализации данного алгоритма, в результате которой будет найден один из элементов, равный K, или будет обнаружено, что такой элемент в массиве отсутствует:

L := 1; R := N;

while L < R do

begin

m := (L + R) div 2;

if a[m] < K then L := m + 1

else R := m

end;

if a[R] = K then write(R) else write(0)

На каждом шаге данного алгоритма длина части массива, в которой мы осуществляем поиск элемента, уменьшается в два раза. То есть, если N = 2ⁱ, то алгоритм будет выполнять i + 1 = log₂N + 1 сравнений. Эта величина существенно меньше, чем N. Так, для N = 10³ число сравнений будет равно 11, а для N = 10⁶ — всего 21.

Алгоритмы сортировки массивов

Задача сортировки массива, то есть перестановки элементов массива так, чтобы они были упорядочены по возрастанию, убыванию или другой аналогичной характеристике, является одной из основных технических задач программирования. С этой задачей мы сталкиваемся и при записи фамилий учеников в классном журнале, и при подведении итогов соревнований, и даже при упорядочении игральных карт, например, при игре в преферанс. Очень часто сортировка используется как первый шаг в алгоритме решения более сложной задачи. Рассмотрим наиболее простые алгоритмы сортировки массивов и подсчитаем их вычислительную сложность (см. “Теория алгоритмов”).

“Пузырьковая” сортировка

Традиционно наиболее простой в реализации считается так называемая “пузырьковая” сортировка. Суть ее в случае упорядочения по неубыванию заключается в следующем. Будем просматривать слева направо все пары соседних элементов: a₁ и a₂, a₂ и a₃, …, a_n-1 и a_n. Если при этом a_i > a_i+1, то элементы меняем местами. В результате такого просмотра массива максимальный элемент окажется на крайнем справа (своем) месте. Об остальных элементах ничего определенного сказать невозможно. Будем просматривать массив снова, исключив из рассмотрения правый элемент. На своем месте теперь окажется уже второй по величине элемент. И так далее. В последнем просмотре будут участвовать только первый и второй элементы. Общее число просмотров при этом равно N–1. Приведем фрагмент программы, реализующий описанный алгоритм:

for j := 1 to n — 1 do

{цикл по просмотрам}

for i := 1 to n — j do

{просмотр массива}

if a[i] > a[i + 1] then

begin

x := a[i];

a[i] := a[i + 1];

a[i + 1] := x

end;

При оценке вычислительной сложности алгоритмов сортировки обычно отдельно подсчитывают количество операций сравнения и количество операций присваивания, т.к. заранее неизвестно, какая из них окажется более трудоемкой, ведь сравниваться между собой могут не только числа, но и строки, и другие достаточно сложные объекты. Иногда обе операции сопоставимы по трудоемкости.

Количество сравнений в данном алгоритме равно

N – 1 + N – 2 + N – 3 + ... + 1 = N(N – 1)/2.

Количество присваиваний в три раза больше, чем число выполненных обменов. В худшем случае обмен будет производиться после каждого сравнения и общее число присваиваний будет равно

3(N – 1 + N – 2 + N – 3 + ... + 1) = 3N(N – 1)/2.

Говорят, что данный алгоритм имеет квадратичную сложность как по числу сравнений, так и по числу присваиваний. “Пузырьковым” он называется потому, что в результате каждого просмотра максимальный из оставшихся элементов оказывается на своем месте — “всплывает”. По-другому такая сортировка называется обменной.

Сортировка “прямым выбором”

Рассмотрим алгоритм сортировки, основанный на принципиально иной идее. Найдем минимальный элемент в массиве и поменяем его с первым элементом массива. В результате он окажется на своем месте. Затем найдем минимальный элемент среди оставшихся и поменяем его со вторым элементом. На N–1-м шаге мы закончим упорядочивание нашего массива. Такой алгоритм называется сортировкой прямым выбором. Приведем фрагмент программы, реализующий описанный алгоритм:

for i := 1 to n — 1 do

begin

mini := i;

for j := i + 1 to n do

{ищем минимальный элемент}

if a[j] < a[mini] then mini := j

{меняем минимальный элемент с i-м}

x := a[i];

a[i] := a[mini];

a[mini] := x

end;

Количество выполняемых операций в данном алгоритме всегда одинаково. Для сравнений оно равно

N – 1 + N – 2 + N – 3 + ... + 1 = N(N – 1)/2,

а для присваиваний — всего 3(N – 1).

Сортировка “подсчетом”

То есть данный алгоритм квадратичный по числу сравнений и линейный (эффективный) по числу присваиваний.

Пусть нам надо отсортировать массив, состоящий из десятичных цифр. Оказывается, что в этом случае существует гораздо более эффективный алгоритм сортировки по сравнению с рассмотренными выше. А именно, подсчитаем во вспомогательном массиве d количество каждой из цифр. Сделать это можно за один проход массива a. Затем заполним массив a заново согласно значениям массива d:

const maxn = 10000;

var d : array[0..9] of integer;

{массив для подсчета}

a : array[1..maxn] of 0..9;{массив цифр}

n, i, j, k : integer;

begin

readln(n); {n — количество цифр}

for i := 1 to n do a[i] := random(10);

for j := 0 to 9 do d[j] := 0;

for i := 1 to n do {подсчет каждой цифры}

d[a[i]] := d[a[i]] + 1;

k := 0;

for j := 0 to 9 do {заполняем a заново}

for i := 1 to d[j] do

k := k + 1;

a[k] := j

end

end.

Заметим, что эта программа работает верно и в случае, когда какой-либо из цифр во вводимой последовательности нет совсем. Подобный алгоритм называют сортировкой подсчетом. Его вычислительная сложность в общем случае составляет 2N + 2m операций, где m — количество различных значений среди элементов в массиве (в нашем примере их было всего 10). Очевидно, что если m Ј N и мы можем отвести память для подсчета количества каждого из m возможных значений для элементов массива, то алгоритм будет иметь линейную сложность относительно N.

Методические рекомендации

Данная тема изучается в курсе программирования на языках высокого уровня. В статье приведены основные задачи, включаемые в контрольно-измерительные материалы по информатике, в том числе в задания ЕГЭ по информатике. Освоение данных алгоритмов на уроках информатики оказывается достаточным для самостоятельного решения в дальнейшем и более сложных задач.

В профильном курсе информатики особое внимание надо уделить анализу вычислительной сложности каждого из рассматриваемых алгоритмов. Подобные задания также могут встретиться на экзаменах.

При изучении “пузырьковой” сортировки стоит обратить внимание на тот факт, что часто массив оказывается отсортированным уже после нескольких первых итераций алгоритма и дальнейшие итерации не нужны. Поэтому, если на каком-то проходе массива ни один обмен произведен не был, то массив уже отсортирован, и работа алгоритма закончена. Соответствующая программа может выглядеть, например, так:

b := true;

j := 0;

while b do begin

{пока есть обмены}

b := false;

j := j + 1;

for i := 1 to n — j do

{просмотр массива}

if a[i] > a[i + 1] then

begin

x := a[i];

a[i] := a[i + 1];

a[i + 1] := x;

b := true;

end

end;

За рамками статьи остались алгоритмы обработки двухмерных массивов — таблиц. Подобная структура данных часто не рассматривается в базовом курсе информатики. При углубленном изучении программирования зачастую достаточно показать, как с помощью вложенных циклов просмотреть все элементы таблицы. Приведем фрагмент программы, печатающий двухмерный массив, состоящий из N строк
и M столбцов, в виде соответствующей таблицы:

for i := 1 to N do

begin

for j := 1 to M do

write(a[i,j]:6:1);

writeln

end;

12. Подпрограммы

Алгоритм, выполняющий некоторую относительно автономную, законченную часть основной задачи, называют вспомогательным алгоритмом, а соответствующую “вспомогательную программу” — подпрограммой (или процедурой). Во многих языках программирования процедура оформляется так же или почти так же, как головная программа.

Когда используют подпрограммы? Во-первых, если один и тот же алгоритм используется несколько раз по ходу решения задачи. Это вполне очевидно: зачем несколько раз писать одни и те же команды? Последовательность операторов, составляющих подпрограмму, определена и записана только в одном месте программы, однако их можно вызвать для выполнения из одной или нескольких точек программы. Одна и та же подпрограмма может обрабатывать различные данные, переданные ей в качестве аргументов. Это не просто выделенный кусок кода — для этого куска кода определены входные и выходные параметры, а от прочих данных он, в идеале, изолирован (хотя многие языки программирования позволяют использовать внутри кода подпрограммы и глобальные переменные).

Во-вторых, в разных программах часто используется большое количество однотипных, шаблонных действий — вывод данных на экран, сортировка чисел по возрастанию в числовых массивах или сортировка списков фамилий по алфавиту, различные алгоритмы поиска необходимых данных в массивах — этот перечень стереотипных работ можно продолжать долго. Совершенно очевидна целесообразность однократного составления таких часто употребляемых вспомогательных алгоритмов, хранение их и последующее использование в самых разнообразных задачах. Наборы таких часто употребимых подпрограмм обычно объединяют в библиотеки подпрограмм. Развитой системой библиотечных подпрограмм обладают такие языки программирования, как С++ и Java.

Но, оказывается, на практике подпрограммами гораздо чаще пользуются, чтобы упростить процесс разработки программы. По мере прогресса в искусстве программирования, как пишет автор языка Pascal Н.Вирт, программы стали создаваться методом последовательных уточнений. На каждом этапе программист разбивает задачу на некоторое число подзадач. Таким образом, подпрограммы — это реализация в языке программирования основного и вспомогательных алгоритмов, на которые, как правило, распадается решение общей задачи в процедурном программировании. Концепция процедур (т.е. подпрограмм) позволяет выделить подзадачу как отдельную подпрограмму, даже если вызываться она будет всего один раз. Допустим, нужно составить какую-нибудь достаточно сложную программу: она должна получать от человека исходные данные, проверяя при этом правильность ввода (чтоб не было ошибок, вроде “32 февраля”), затем выполнять несколько разных вычислений, наконец, — красиво выводить результаты на экран. Можно попытаться написать сразу всю программу целиком. Однако она скорее всего получится очень большой и настолько запутанной, что поиск любой самой простой ошибки займет много времени (а написать даже не очень большую программу сразу без ошибок практически невозможно). Но можно поступить по-другому. Сначала разобьем решение задачи на несколько этапов. Получится программа примерно такого вида:

начало программы

ввод_данных

проверка данных

обработка данных

вывод_результатов

конец

Мы еще не знаем, как будут реализовываться эти этапы, но то, что они необходимы, нам известно; не возникает вопросов и с их последовательностью. Далее, каждый из этапов разбиваем на более мелкие, затем, при необходимости — еще. Так продолжаем, пока подзадачи не окажутся настолько мелкими, что каждую из них можно будет записать с помощью небольшой простой и понятной процедуры. Можно сказать, что подпрограммы являются основными строительными блоками программы. Такой способ разработки программ называют проектированием методом сверху вниз.

Каковы достоинства этого метода? Во-первых, сокращение времени разработки больших программ: на решение 10 простых задач обычно нужно гораздо меньше времени, чем на одну, в 10 раз более сложную. Во-вторых, локализация мест ошибок при отладке программ: разобраться в работе процедуры и найти возможную ошибку намного проще, если эта процедура — короткая. В-третьих, относительная автономность модификации программы: когда нужно будет что-либо изменить в программе, переделывать придется не всю ее, а только некоторые процедуры. Наконец, такой метод позволяет легко распределить работу между несколькими программистами: при разработке процедуры абсолютно не важно, что содержится внутри других.

Процедуры и функции

Во многих языках программирования явно (как в Pascal) или неявно (как в С и С++) различают два вида подпрограмм — процедуры и функции. Основное отличие функций от процедур заключается в том, что функция возвращает результат некоторого типа.

После описания функции ее, как лексическую единицу, можно использовать в выражениях наряду со стандартными функциями. Функция активируется только при вызове ее из тела основной программы или из другой уже вызванной подпрограммы (процедуры или функции). При вызове функции указывается имя функции и конкретные параметры (их называют фактические параметры), необходимые для вычисления функции.

В описании процедуры или функции задается список формальных параметров. Каждый параметр, описанный в этом списке, является локальным по отношению к описываемой процедуре или функции, т.е. на него можно ссылаться по его имени из данной подпрограммы, но не из основной программы.

Приведем пример программы на языке Pascal нахождения максимума из трех чисел, использующей описание функции max нахождения максимума из двух чисел:

var x, y, z: integer;

function max(a, b: integer): integer;

begin

if a > b then max := a

else max := b

end;

begin

readln(x, y, z)

writeln(max(max(x,y),z))

end.

Процедура либо вообще не возвращает результат, либо делает это через параметры. Процедура активируется (вызывается) с помощью оператора процедуры. Он представляет собой то же имя, что и название процедуры, с перечислением в скобках фактических параметров (процедура параметров может и не содержать, например, процедура очистки экрана).

Приведем пример описания процедуры на языке Pascal, которая печатает первые N элементов массива. Используем эту процедуру для печати различных частей массива:

type aa = array[1..100] of integer;

var a: aa;

i: integer;

procedure print(n: integer; var m: aa);

var i: integer;

begin

for i := 1 to n do

write(m[i], ' ');

writeln

end;

for i := 1 to 100 do a[i] := random(100);

for i := 1 to 100 do print(a,i)

end.

Процедура или функция является рекурсивной, если она прямо или косвенно вызывает сама себя. То есть либо при описании функции или процедуры используется обращение к ней же самой, но с другим набором параметров, либо подпрограмма вызывает какую-либо другую подпрограмму, в описании которой содержится вызов исходной (например, процедура A вызывает процедуру В, а процедура В вызывает процедуру А).

Рекурсивный вариант реализации алгоритма обычно выглядит изящнее и дает более компактный текст программы, но исполняется медленнее. Приведем пример уместного использования рекурсивного алгоритма. Рассмотрим алгоритм эффективного возведения вещественного числа x в целую неотрицательную степень n, основанный на следующих очевидных соотношениях:

x⁰ = 1; если n — нечетное, то xⁿ = xⁿ–1 · n, в противном случае xⁿ = (x²)^n/2.

Зададим по данному описанию рекурсивную функцию на языке Pascal:

function power(x:real; n:integer):integer;

begin

if n = 0 then power := 1

else if n mod 2 = 0 then

power := power(x*x,n div)

else power := power(x,n-1)*x

end;

Данная функция для вычисления xⁿ будет использовать не более 2log₂n умножений, а ее нерекурсивный аналог написать и отладить существенно сложнее.

Процедурное программирование

Процедурное программирование — это одна из парадигм программирования.

Парадигма программирования представляет (и определяет) то, как программист подходит к реализации алгоритма и проектированию программы. Так, процедурное программирование основано на представлении программы, как определенной последовательности вызова процедур.

Процедурное программирование — оформившаяся в начале 70-х годов XX века идея разработки программ. Это фундаментальная концепция, являющаяся основой всех современных подходов к проектированию и реализации. В то же время суть ее проста и отражает широко известные методы, заключающиеся в поиске и реализации некоторого базового набора элементов, комбинация которых дает решение задачи.

Если концепция структурного программирования предлагает некоторый универсальный алгоритмический базис, то процедурное программирование состоит в разработке под конкретную задачу или круг задач (предметную область) собственного базиса в виде набора подпрограмм, позволяющего наиболее эффективно по целому ряду критериев построить программный комплекс. С применением процедурного программирования появились возможности коллективной разработки программ как набора “независимых” частей, последовательного уменьшения сложности методом разбиения сложной задачи на более простые подзадачи, наконец, возможности повторного использования созданного ранее кода.

Решение общей задачи даже в простейших случаях представляет собой многоступенчатый процесс расчленения на все более простые действия. Конечно, можно составить весь алгоритм без явного выделения вспомогательных действий, но такую программу будет не только неудобно составлять и отлаживать, ее будет чрезвычайно сложно читать и практически невозможно совершенствовать.

Обычно процедурная программа состоит из главной подпрограммы (она нужна для определения начала и конца общего алгоритма), которая что-то делает сама, а что-то поручает вызываемым на выполнение вспомогательным подпрограммам, которые, в свою очередь, делают что-то сами и, возможно, вызывают на выполнение другие вспомогательные подпрограммы и т.д. После завершения подпрограмма должна возвратить управление в точку вызова — точнее, на оператор, следующий за вызовом подпрограммы.

Процедуры и функции позволяют создавать большие структурированные программы, которые можно делить на части. Это дает преимущества в следующих ситуациях:

1. Если программа большая, разделение ее на части облегчает создание, тестирование и ее сборку.

2. Если программа большая и повторная компиляция всего исходного текста занимает много времени, разделение ее на части экономит время компиляции.

3. Если процедуру надо использовать в разных случаях разным образом, можно записать ее в отдельный файл и скомпилировать отдельно.

Более современная парадигма программирования — объектно-ориентированное программирование (см. статью “Объектно-ориентированное программирование”) — фактически включает в себя и процедурную парадигму.

Методические рекомендации

Данная тема возникает при изучении программирования на языках высокого уровня или на языке исполнителя, например, LOGO. Слово подпрограмма (routine) использовалось уже в 1949 г. при программировании на машине EDSAC, которую принято считать первой построенной машиной с хранением программ в памяти. Подпрограмма является основным строительным блоком в императивном программировании (такое программирование описывает процесс выполнения программы в виде инструкций, изменяющих состояние исполнителя, альтернативой императивному программированию служит декларативное — логическое или функциональное — программирование).

Подпрограммы используются главным образом для целей абстракции. Под абстракцией понимается действие, состоящее в выборе для дальнейшего изучения или использования небольшого числа свойств объекта и изъятии из рассмотрения остальных свойств, которые нам в данный момент не нужны. Основное свойство, которое выделяется при написании подпрограммы, — это то, что она делает. Главное свойство, которое опускается из рассмотрения, — как она это делает. В некотором смысле использование подпрограммы — в точности то же самое, что и использование любой другой операции, применимой в том или ином языке программирования, например, +. А написание подпрограммы — это расширение языка путем включения в него новой операции.

Существуют подходы к изучению языка программирования, в которых подпрограммы предлагается использовать на самых ранних этапах изучения языка, а в таких языках, как С, этого вообще практически не избежать. При этом допускается сначала не полное понимание того, что же представляют собой подпрограммы, какую память они используют и как происходит передача параметров при их вызове. Возможно, такой подход позволяет сразу вырабатывать правильный стиль написания структурированных программ. Однако учебные программы, которые ученикам приходится писать на первых этапах обучения, зачастую не требуют детализации с помощью процедур и функций, поэтому изучение последних можно отложить и на более поздний срок (или опустить совсем, если курс программирования является чисто ознакомительным).

В некоторых языках программирования, например в языке Pascal, достаточно сложным является механизм передачи параметров и следующие из него правила разделения параметров на параметры-значения и параметры-ссылки. Попробуйте объяснить учащимся этот механизм, только в этом случае они смогут грамотно и без ошибок выбирать тип параметров при описании процедур и функций.

Подробное изучение данной темы в 10–11-х профильных классах заканчивается рассмотрением рекурсии, ее применением и механизмом реализации в тех языках программирования, в которых она разрешена.

13. Разработка программ

Программирование — одна из первых автоматизированных информационных технологий — начиная с 70-х годов прошлого столетия начала новый виток бурного развития. Связано это в первую очередь с информатизацией общества в целом: сегодня практически все виды человеческой деятельности в той или иной степени автоматизированы, для чего разрабатывается специальное программное обеспечение. В сфере разработки программного обеспечения работают миллионы людей. Программирование как область человеческой деятельности характеризуется определенными этапами и способами создания законченного программного продукта, формами организации взаимодействия разработчиков-программистов. И в первую очередь среди этих характеристик важно выделить парадигмы и технологии программирования.

Парадигма программирования

Слово парадигма (от гр. paraRdeigma) означает пример, образец. Известный американский философ Кун Томас Самюэл дал следующее определение этого понятия. Парадигма — совокупность знаний, методов и ценностей, безоговорочно разделяемых членами научного сообщества. Под парадигмой программирования сегодня понимают некоторый взаимосвязанный набор идей и рекомендаций, определяющих стиль написания программ. Парадигма программирования представляет (и определяет) то, как программист видит выполнение программы. В современном программировании сложилось несколько видов парадигм программирования: императивное, процедурное (см. “Подпрограммы”), объектно-ориентированное, декларативное программирование, к которому относят логическое и функциональное программирование.

Так, в объектно-ориентированном программировании (см. “Объектно-ориентированное программирование”) программист рассматривает программу как набор взаимодействующих объектов, тогда как в функциональном программировании программа представляется в виде цепочки вычисления функций. В императивном программировании исполнителю программы четко предписывается последовательность выполняемых действий, в то время как в функциональном программировании способ решения задачи описывается при помощи зависимости функций друг от друга (в том числе возможны рекурсивные зависимости), но без указания последовательности шагов. В логическом программировании программа представляет собой множество пар (логическое условие, новые факты), при этом так же, как и в функциональном программировании, программист остается в неведении о методах, применяемых при вычислении, и последовательности исполнения элементарных действий. БoRльшая часть ответственности за эффективность вычислений в логическом и функциональном программировании перекладывается на транслятор используемого языка программирования. Успешность реализации выбранной парадигмы программирования во многом определяется выбором соответствующего языка программирования (см. “Языки программирования”).

Вне зависимости от выбранной парадигмы разработка программы включает в себя следующие этапы: проектирование (уточнение способов организации данных — структур и типов данных (см. “Структуры данных”, “Типы данных”), разработка алгоритма и запись его на выбранном языке программирования), тестирование, отладка и документирование программы. Промышленная разработка программ сталкивается с проблемами стоимости и надежности. Некоторые программы содержат миллионы строк исходного кода, которые, как ожидается, должны правильно исполняться в реальных условиях. Для эффективной разработки больших или сложных программ используются различные технологии программирования.

Как правило, программы разрабатываются в расчете на то, чтобы ими могли пользоваться люди, не участвующие в их разработке (их называют пользователями). Программа или логически связанная совокупность программ на носителях данных, снабженная программной документацией, называется программным средством (ПС). Программа позволяет осуществлять некоторую автоматическую обработку данных на компьютере. Программная документация позволяет понять, какие функции выполняет та или иная программа ПС, как подготовить исходные данные и запустить требуемую программу для выполнения, а также, что означают получаемые результаты (или каков эффект выполнения этой программы). Кроме того, программная документация помогает разобраться в самой программе, что необходимо, например, при ее модификации.

В соответствии с обычным значением слова “технология” (см. “Информационные технологии”) под технологией программирования понимается совокупность производственных процессов, приводящая к созданию требуемого ПС, а также описание этой совокупности процессов. Другими словами, под технологией программирования понимается как технология разработки программных средств, включая в нее все процессы, начиная с момента зарождения идеи этого средства, так и процессы, связанные с созданием необходимой программной документации.

По мере повышения мощности компьютеров и развития средств и методологии программирования растет и сложность решаемых на компьютерах задач, что привело к повышенному вниманию к технологии программирования. Резкое удешевление стоимости компьютеров и в особенности стоимости хранения информации на компьютерных носителях привело к широкому внедрению компьютеров практически во все сферы человеческой деятельности, что существенно изменило направленность технологии программирования. Сформировалось понятие качества ПС, в котором акценты ставятся не только на его эффективности, но и на удобстве работы с ним для пользователей (не говоря уже о его надежности). Широкое использование компьютерных сетей привело к интенсивному развитию распределенных вычислений, дистанционного доступа к информации и электронного способа обмена сообщениями между людьми. Компьютерная техника из средства решения отдельных задач все более превращается в средство информационного моделирования реального и мыслимого мира. Все это ставит перед технологией программирования новые и достаточно трудные проблемы.

В 50-е годы мощность компьютеров была невелика (компьютеры первого поколения), а программирование для них велось в основном в машинном коде. Решались главным образом научно-технические задачи (расчет по формулам), задание на программирование уже содержало, как правило, достаточно точную постановку задачи. Использовалась интуитивная технология программирования: почти сразу приступали к составлению программы по заданию, при этом часто задание несколько раз изменялось, минимальная документация оформлялась уже после того, как программа начинала работать. Тем не менее именно в этот период родилась фундаментальная для технологии программирования концепция модульного программирования (для преодоления трудностей программирования в машинном коде). Появились первые языки программирования высокого уровня.

В 60-е годы можно было наблюдать бурное развитие и широкое использование языков программирования высокого уровня (АЛГОЛ-60, ФОРТРАН, КОБОЛ и др.), роль которых в технологии программирования явно преувеличивалась. Надежда на то, что эти языки решат все проблемы разработки больших программ, не оправдалась. В результате повышения мощности компьютеров и накопления опыта программирования на языках высокого уровня быстро росла сложность решаемых на компьютерах задач: стало понятно, что важно не только то, какой язык программирования используется, но и то, как создается программа. Появление прерываний в компьютерах 2-го поколения привело к развитию мультипрограммирования и созданию больших программных систем. Последнее стало возможным с использованием коллективной разработки, которая поставила ряд серьезных технологических проблем.

В 70-е годы широкое распространение и обоснование получили технологии нисходящей разработки и структурного программирования, модульного программирования, создание методики управления коллективной разработкой ПС, появление инструментальных программных средств (программных инструментов) поддержки технологии программирования. Развитие технологии структурного программирования связано с публикацией письма Эдсгера Дийкстры в Ассоциацию вычислительной техники (1968 г.) (ACM — Association for Computing Machinery), озаглавленного так: “О вреде использования операторов GOTO”. В те времена программы писались с активным использованием операторов безусловного перехода. Обращая внимание на недостатки таких программ, Дийкстра предложил концепцию структурного программирования, позволяющую избежать использования этих операторов. Концепция Дийкстры основывалась на доказательстве Бома и Джакопини, что для записи любой программы в принципе достаточно только трех конструкций управления — последовательного выполнения, ветвления и цикла, то есть что теоретически необходимость в использовании операторов перехода отсутствует (см. также статью “Алгоритмические конструкции”).

Следующий шаг в развитии структурного программирования связан с введением аппарата подпрограмм, позволяющих разбивать структурную программу на обозримые по своим размерам части. При таком подходе программа пишется в терминах вызова подпрограмм верхнего уровня, которые реализуются при помощи подпрограмм более низкого уровня, и т.д. На основе нисходящего структурного программирования (программирование по технологии “сверху вниз”, см. статью “Подпрограммы”) была разработана технология коллективной разработки больших программных комплексов.

80-е и 90-е годы знаменательны широким охватом человеческого общества международной компьютерной сетью, персональные компьютеры стали подключаться к ней как терминалы. Это поставило ряд проблем регулирования доступа к компьютерно-сетевой информации (как технологического, так и юридического и этического характера). Остро встала проблема защиты компьютерной информации и передаваемых по сети сообщений. Стали бурно развиваться CASE-технологии (Computer-Aided Software Engineering) разработки ПС и связанные с ними формальные методы спецификации программ.

В связи с широким внедрением персональных компьютеров во все сферы человеческой деятельности важной составляющей разработки программ стало проектирование взаимодействия пользователя с программой (ее интерфейса). Широкое применение графического пользовательского интерфейса ведет к тому, что многие аспекты разработки приложений лежат за пределами математики и даже алгоритмики и требуют серьезного внимания к психологическим основам взаимодействия “человек — машина”. При разработке графического интерфейса большую роль играет технология визуального программирования, в которой программист оформляет свою будущую программу, используя некоторый конструктор элементов интерфейса, и видит результаты своей работы еще до запуска самой программы.

В последнее время получила распространение еще одна технология разработки программ — экстремальное программирование. По этой технологии с самого начала программа пишется в предположении, что заказчик заранее не может сформулировать все требования к программному продукту, поэтому программа все время будет меняться, в том числе в процессе работы над ней. Одним из элементов экстремального программирования является парное программирование. Оно означает, что любой кусок кода создается парами людей, программирующими одну задачу сидя за одним рабочим местом. Один программист работает над кодированием конкретных частей программы, другой сосредоточен на картине в целом и непрерывно просматривает код, производимый первым программистом с целью сделать его абсолютно прозрачным. Время от времени люди меняются ролями. Пары не фиксированы: рекомендуется “перемешивать” их насколько это возможно, так чтобы каждый знал, что делает каждый другой, и все были знакомы со всей системой в целом.

Отладка и тестирование программ

Отладка программы — это деятельность, направленная на обнаружение и исправление ошибок в программе. Обнаружить ошибки, связанные с нарушением правил записи программы на языке программирования (синтаксические и семантические ошибки), помогает используемая система программирования. Пользователь получает сообщение об ошибке, исправляет ее и снова повторяет попытку исполнить программу.

Тестирование программы — это процесс выполнения программы с целью обнаружения ошибки в программе на некотором наборе данных, для которого заранее известен результат применения или известны правила поведения этих программ. Указанный набор данных называется тестовым или просто тестом. Прохождение теста — необходимое условие правильности программы. На тестах проверяется правильность реализации программой запланированного алгоритма. Таким образом, отладку можно представить в виде многократного повторения трех процессов: тестирования, в результате которого может быть констатировано наличие в ПС ошибки, поиска места ошибки в программах и документации ПС и редактирования программ и документации с целью устранения обнаруженной ошибки.

Успех отладки в значительной степени предопределяет рациональная организация тестирования. При отладке отыскиваются и устраняются в основном те ошибки, наличие которых в программе устанавливается при тестировании. Тестирование не может доказать правильность программы, в лучшем случае оно может продемонстрировать наличие в нем ошибки. Другими словами, нельзя гарантировать, что тестированием программы на соответствующих наборах тестов можно установить наличие каждой имеющейся в программе ошибки. Поэтому возникают две задачи. Первая: подготовить такой набор тестов и применить к ним программу, чтобы обнаружить в нем по возможности большее число ошибок. Однако чем дольше продолжается процесс тестирования (и отладки в целом), тем большей становится стоимость программы. Отсюда вторая задача: определить момент окончания отладки программы (или отдельной ее компоненты). Признаком возможности окончания отладки является полнота охвата тестами, к которым применена программа, множества различных ситуаций, возникающих при выполнении программы, и относительно редкое проявление ошибок в программе на последнем отрезке процесса тестирования. Последнее определяется в соответствии с требуемой степенью надежности программы, указанной в спецификации ее качества.

Для оптимизации набора тестов, т.е. для подготовки такого набора тестов, который позволял бы при заданном их числе (или при заданном интервале времени, отведенном на тестирование) обнаруживать большее число ошибок, необходимо, во-первых, заранее планировать этот набор и, во-вторых, использовать рациональную стратегию планирования тестов.

Таким образом, тестирование и отладка включают в себя синтаксическую отладку; отладку семантики и логической структуры программы; тестовые расчеты и анализ результатов тестирования. Затем идет совершенствование программы.

Документирование программы

При разработке ПС создается большой объем разнообразной документации. Продуманная документация программных разработок облегчает совместную работу над проектом больших групп программистов, позволяет подключать новых людей, избегать дублирования многих действий. В итоге повышается производительность труда программистов и увеличивается надежность кода. Кроме того, документация необходима для управления разработкой ПС и для передачи пользователям информации, необходимой для применения и сопровождения ПС. На создание этой документации приходится большая доля стоимости ПС.

Всю документацию можно разбить на две группы:

· документы управления разработкой ПС;

· документы, входящие в состав ПС.

Документы управления разработкой ПС протоколируют процессы разработки и сопровождения ПС, обеспечивая связи внутри коллектива разработчиков и между коллективом разработчиков и менеджерами — лицами, управляющими разработкой.

Пользовательская документация ПС объясняет пользователям, как они должны действовать, чтобы применить данное ПС. Она необходима, если ПС предполагает какое-либо взаимодействие с пользователями. К такой документации относятся документы, которыми руководствуется пользователь при инсталляции ПС, при применении ПС для решения своих задач и при управлении ПС (например, когда данное ПС взаимодействует с другими системами). Эти документы частично затрагивают вопросы сопровождения ПС, но не касаются вопросов, связанных с модификацией программ.

Системы программирования

Написание даже учебных программ практически невозможно без соответствующей системы программирования (среды программирования или интегрированной среды разработки IDE — integrated development environment). Первая среда разработки была создана для языка Basic. Среда программирования включает прежде всего текстовый редактор, позволяющий конструировать программы на заданном языке программирования, а также инструменты, позволяющие компилировать или интерпретировать программы на этом языке, тестировать и отлаживать полученные программы. Кроме того, могут быть и другие инструменты, например, для анализа программ, контроля версий, автоматического создания кода элементов интерфейса и др.

Различают следующие классы сред программирования (см. схему):

· среды общего назначения;

· языково-ориентированные среды.

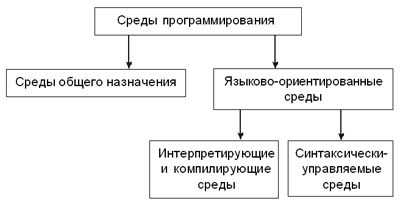
Классификация инструментальных сред программирования

Среды общего назначения содержат набор программных инструментов, поддерживающих разработку программ на разных языках программирования. Языково-ориентированная инструментальная среда программирования предназначена для поддержки разработки программы на каком-либо одном языке программирования, и знания об этом языке существенно использовались при построении такой среды. Вследствие этого в такой среде могут быть доступны достаточно мощные возможности, учитывающие специфику данного языка. Такие среды разделяются на два подкласса.

Классификация инструментальных сред программирования

Интерпретирующие и компилирующие среды, помимо текстового редактора, обеспечивают интерпретацию или компиляцию программ на данном языке программирования. Синтаксически-управляемая среда программирования уже на этапе написания текста программы использует знание синтаксиса языка программирования, на который она ориентирована.
В такой среде вместо текстового используется синтаксически-управляемый редактор, позволяющий пользователю использовать различные шаблоны синтаксических конструкций (в результате этого разрабатываемая программа по окончании написания всегда будет синтаксически правильной). Наряду с промышленными синтаксически-управляемыми средами, например для языка JAVA, подобными свойствами обладают и некоторые специально разработанные учебные среды, например, для языка Pascal.

Многие современные среды программирования поддерживают технологию визуального программирования. В среде визуальной разработки наиболее распространенные блоки программного кода представлены в виде графических объектов. Программист располагает на будущих окнах своей программы необходимые элементы, позиционирует, устанавливает нужные размеры, меняет их свойства. Остается написать только программный код, реализующий свойства элементов интерфейса, доступных только во время работы приложения: описание реакций на события — появление окна, нажатие на кнопку и др. Для задания каких-либо свойств элементу разрабатываемого приложения вовсе не обязательно писать строки программного кода, достаточно изменить это свойство в инспекторе объектов (так называемом “мониторе свойств выбранного элемента”). Это изменение автоматически дополнит или модифицирует программный код. Преимуществами этой технологии являются быстрота разработки, относительная легкость освоения, стандартизация внешнего вида программ. Недостатки заключаются в том, что часть кода не контролируется программистом, код может получиться менее эффективным, нежели при написании его “вручную”. Примерами визуальных сред программирования являются системы программирования Borland Delphi и Visual Basic.

Государственный образовательный стандарт предусматривает изучение в профильной школе принципов разработки программ и знакомство с системами программирования. Очевидно, что изучение данных тем невозможно в отрыве от изучения языка программирования и практических занятий по написанию программ. Знакомство со средами программирования обычно начинается еще в начальной школе или 5–7-х классах основной школы с работы в среде учебного исполнителя или в среде LOGO. Наиболее совершенные версии последней (например, LOGO-миры) фактически представляют собой современные среды, поддерживающие визуальную технологию разработки программ и объектно-ориентированную парадигму программирования.

Работа со средами программирования для универсальных языков программирования высокого уровня (см. “Языки программирования””) обычно начинается в 8–9-х классах с системы Borland Pascal или Quick Basic. На этом этапе учащиеся знакомятся с принципами отладки программ, получают навыки их тестирования. В профильном курсе информатики для старших классов средней школы возможна продуктивная работа с современными профессиональными средами программирования, такими, как Borland Delphi и Visual Basic. Курс по освоению последней среды подкреплен материалами учебника Н.Д. Угриновича “Информатика и информационные технологии. Учебник для 10–11-х классов”, 2005, изд-во “БИНОМ. Лаборатория Знаний”. Здесь на первый план выходит овладение визуальной технологией разработки программы, оптимизация ее интерфейса. Несмотря на то что в учебное время работа с подобными средами ведется практически в ознакомительном режиме, зачастую этого достаточно, чтобы наиболее заинтересованные школьники получили мощный толчок для самостоятельного углубленного освоения возможностей системы. В результате некоторые из них уже в школе создают прикладные программы практически профессионального уровня, которые с успехом демонстрируют на различных конференциях и конкурсах программ.

14. Способы записи алгоритмов

Для записи алгоритмов (см. статью “Алгоритм”) существуют различные формы записи: словесная, блок-схема, программа на каком-либо алгоритмическом языке, нормальный алгоритм Маркова, машина Тьюринга, машина Поста и др. Такое многообразие форм записи алгоритмов обусловлено разными целями работы с алгоритмами. Математики, доказывая правильность алгоритма, естественно, будут работать с формальным представлением алгоритма, например, в виде нормального алгоритма Маркова. Учитель, объясняя сложный алгоритм в школе, может для наглядности использовать запись в виде блок-схемы. Опытные программисты запишут алгоритм в виде программы. При изучении в школе темы “Алгоритмизация и программирование” основными являются следующие способы представления алгоритмов: запись алгоритмов в виде текстовых описаний, блок-схемы и запись в виде программы для того или иного исполнителя (см. “Исполнители алгоритмов”).

Здесь нельзя не упомянуть и учебный Алгоритмический язык, введенный в школьную информатику Ершовым, затем используемый в учебниках А.Г. Кушниренко, А.Г. Гейна, И.Г. Семакина. Учебный Алгоритмический язык — это русскоязычный структурный псевдокод. Педагогический опыт показывает эффективность на начальных этапах обучения программированию “трехступенчатой” методики разработки программ: блок-схема — Алгоритмический язык — язык программирования (лучше всего — Паскаль, поскольку АЯ — паскалеобразен).

Текстовая (словесно-формульная) форма записи алгоритмов обычно используется для алгоритмов, ориентированных на исполнителя-человека. Алгоритм задается в произвольном изложении на естественном языке, возможно, с использованием формул. Описание может быть разбито на пункты (шаги алгоритма). Команды такого алгоритма выполняются в естественной последовательности, если не оговорено противного. Словесный способ записи алгоритмов допускает неоднозначность толкования отдельных предписаний, особенно если система команд исполнителя того или иного алгоритма (конкретного человека) четко не фиксирована.

Такой способ широко распространен при описании решения математических, химических, физических и бытовых задач, в том числе в соответствующих школьных учебниках. В решении этих задач практически отсутствуют циклические алгоритмические конструкции (см. “Алгоритмические конструкции”). Алгоритмическая конструкция ветвление записывается либо с помощью одного предложения: “Если дискриминант меньше нуля, то у уравнения нет решения, в противном случае …”, либо с помощью указания, какой из пунктов алгоритма нужно выполнять в том или ином случае: “Если при звонке по телефону гудки короткие, то п. 4, а если длинные, то п. 6”.

Блок-схемы

Блок-схемы алгоритмов — это графическое описание алгоритмов как последовательности действий. Описание алгоритма с помощью блок-схем осуществляется рисованием последовательности функциональных блоков, каждый из которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками. Написание алгоритмов с помощью блок-схем регламентируется ГОСТом. Внешний вид основных блоков, применяемых при написании блок-схем, приведен на рисунке:

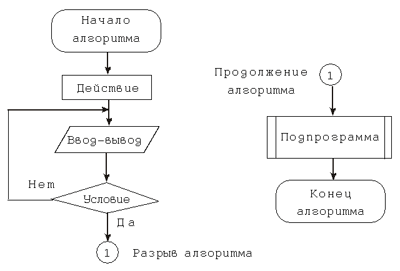
В схеме алгоритма каждому типу действий соответствует геометрическая фигура. Фигуры соединяются линиями переходов, определяющими очередность выполнения действий. В блок-схемах всегда есть начало и конец, обозначаемые эллипсами, между ними — последовательность шагов алгоритма, соединенных стрелками. Шаги бывают безусловными (изображаются прямоугольниками, параллелограммами) и условными (изображаются ромбами). Из ромба всегда выходят две стрелки — одна означает дальнейший путь, в случае выполнения условия (обозначается обычно словом “да” или “+”), другая — невыполнение (слово “нет” или “–”). Ввод с клавиатуры или вывод на экран значения выражения изображается параллелограммом. Команда, выполняющая обработку действий (обычно команда присваивания), изображается в прямоугольнике.

Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным. Однако сохраняет и некоторые недостатки. С помощью блок-схем можно записывать в том числе и неформальные (например, бытовые) алгоритмы, содержание функциональных блоков при этом остается относительно произвольным. Отсутствие явных ограничений на правила перехода в блок-схемах приводит к тому, что в них не всегда можно явно выделить базовые алгоритмические конструкции, т.е. алгоритм, записанный таким образом, может не соответствовать требованиям структурного программирования. Наконец, обозримыми являются блок-схемы только для небольших алгоритмов. При составлении блок-схем надо внимательно следить за структурностью алгоритма, т.е. блок-схема произвольного алгоритма должна быть композицией схем основных алгоритмических конструкций, в противном случае программирование подобного алгоритма будет затруднено.

При записи алгоритма как в словесной форме, так и в виде блок-схем допускается определенный произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм. Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы, в частности, компьютеры. Поэтому алгоритм, предназначенный для того или иного исполнителя, должен быть записан на “понятном” ему языке, c использованием только СКИ (см. статью “Исполнитель алгоритмов”). И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем. Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык для компьютера-исполнителя принято называть языком программирования (см. статью “Языки программирования”), а запись алгоритма на этом языке — программой для компьютера.

Программами являются и запись нормальных алгоритмов Маркова, и машина Тьюринга для решения конкретной задачи (см. статью “Теория алгоритмов”).

Методические рекомендации

На разных ступенях школьного образования используются различные способы записи алгоритмов. В начальной школе это в первую очередь словесная форма записи, реже — блок-схемы. При работе с учебными исполнителями, например, входящими в комплект “Роботландии”, алгоритмы записываются на языке соответствующего исполнителя, что является очень важным шагом к осмыслению понятия формализации алгоритмов.

В базовом курсе информатики алгоритмы записывают с помощью блок-схем, на школьном алгоритмическом языке или языке программирования высокого уровня. В школьном курсе информатики наиболее часто используют такие языки, как Pascal и Basic.

В профильной школе возможен переход к профессиональным версиям языков программирования, например, Delphi или Visual Basic. Однако неоправданным является построение сквозного курса информатики, в котором акцент делается на изучение именно языков программирования, например, сначала изучается Basic, потом Pascal, а потом С. Если на освоение программирования можно выделить достаточное число часов, то правильнее отвести их на изучение различных алгоритмов, в том числе выходящих за рамки базового курса информатики, а также на знакомство с современными технологиями и парадигмами программирования (см. “Разработка программ”, “Объектно-ориентированное программирование”).

15. Структуры данных

Необходимым условием построения алгоритма является формализация данных, т.е. приведение информации к некоторой информационной модели (см. “Информационные модели”), уже описанной и исследованной. Когда такая модель найдена, говорят, что определена абстрактная структура данных.

Абстрактная структура данных описывает признаки и свойства объекта, взаимосвязь между элементами объекта, а также возможные операции над данным объектом или классом объектов.

Одной из задач информатики является нахождение форм представления информации, удобных для компьютерной обработки. Информатика как точная наука работает с формальными (описанными математически строго) объектами. Такими объектами — базовыми абстрактными структурами данных, используемыми в информатике, являются:

· целые числа;

· вещественные числа;

· символы;

· логические значения.

Для компьютерной обработки этих объектов в языках программирования существуют соответствующие типы данных (см. “Типы данных”). Базовые объекты можно объединять в более сложные структуры, добавляя операции уже над структурой в целом и правила доступа к отдельным элементам этой абстрактной структуры данных.

К таким абстрактным структурам данных относятся:

· векторы (конечные массивы);

· таблицы (матрицы), а в общем случае — многомерные массивы;

· графы;

· динамические структуры:

o последовательности символов, чисел;

o строки;

o списки;

o очереди;

o стеки;

o деревья;

o графы.

Удачный выбор структуры данных часто является залогом создания эффективного алгоритма и программы, его реализующей: используя аналогию структур данных и реальных объектов, можно находить эффективные решения задач.

Заметим, что перечисленные структуры существуют независимо от их реализации при программировании. С этими структурами данных работали и в XVIII, и в XIX веках, когда еще не придумали вычислительную машину. Мы можем разрабатывать алгоритм в терминах абстрактной структуры данных, но для реализации алгоритма в конкретном языке программирования необходимо найти способ ее представления в терминах типов данных и операторов, поддерживаемых данным языком программирования (см. “Операторы языка программирования”). Для компьютерного представления абстрактных структур используются структуры данных, которые представляют собой набор переменных, возможно различных типов данных, объединенных определенным образом. Для конструирования таких структур, как вектор, таблица, строка, последовательность, в большинстве языков программирования присутствуют стандартные типы данных: одномерный массив, двухмерный массив, строка, файл (реже список) соответственно. Организацию остальных структур данных, в первую очередь динамических структур, размер которых меняется во время выполнения программы, программисту приходится осуществлять самостоятельно, используя базовые типы данных. Рассмотрим такие структуры подробнее.

Списки

Линейный список — последовательность линейно связанных элементов, для которых разрешены операции добавления элементов в произвольное место списка и удаление любого элемента. Линейный список однозначно задается указателем на начало списка. Типовыми операциями над списками являются: обход списка, поиск заданного элемента, вставка элемента сразу после или перед определенным элементом, удаление заданного элемента, объединение двух списков в один, разбиение одного списка на два и более списков и т.п.

В линейном списке для каждого элемента, кроме первого, есть предыдущий элемент; для каждого элемента, кроме последнего, есть следующий элемент. Таким образом, все элементы списка упорядочены. Однако обработка линейного односвязного списка не всегда удобна, т.к. отсутствует возможность движения в противоположную сторону — от конца списка к началу. В линейном списке можно обойти все элементы, только двигаясь последовательно от текущего элемента к следующему, начиная с первого, прямой доступ к i-му по счету элементу невозможен.

Пример 1. Порядок следования записей фамилий читателей в компьютере библиотекаря определяет отношение “предыдущий–следующий”. Как правило, сами записи имеют дополнительное свойство — они упорядочены по алфавиту. Над этим списком реализованы операции добавления нового читателя и, при необходимости, удаления старого. Если к тому же ведутся записи выданных каждому читателю книг, то каждую такую запись удобно представлять опять же с помощью списка выданных книг.

Кольцевые списки — такая же структура, как и линейный список, но имеющая дополнительную связь между последним и первым элементом, то есть следующим за последним элементом является первый элемент.

В кольцевом списке в отличие от линейного все элементы равноправны (поскольку для каждого элемента определены и предыдущий, и следующий элементы). Выделение “первого” и “последнего” элементов в кольцевом списке весьма условно, так как собственно структура списка не имеет явно выделенных элементов!

Пример 2. Во многих играх дети используют считалочки, чтобы выбрать ведущего, разделиться на команды и т.п. Как правило, считалочки длинные, и дети (сами того не зная) организуют кольцевой список. Отношение “предыдущий–следующий” определяется тем, в какую сторону ведущий считает. Типичная операция в такой структуре — удаление элемента из списка с сохранением его кольцевой структуры.

Линейные списки, в которых операции вставки, удаления и доступа к значениями элементов выполняются только с крайними элементами (первым или последним), получили специальные названия.

Стек — частный случай линейного односвязного списка, для которого определены две операции: добавление элемента в вершину стека (перед первым элементом) и удаление элемента из вершины стека (удаление первого элемента).

Пример 3. Рассмотрим задачу определения сбалансированности скобок различных видов в арифметическом выражении. Например, требуется проанализировать, сбалансированы ли скобки в выражении, содержащем круглые и квадратные скобки: ? Для решения этой задачи будем использовать динамическую структуру данных стек. Приведем алгоритм решения этой задачи по шагам. Будем использовать следующие обозначения:

i — номер анализируемого символа;

n — количество символов в выражении.

1. i = 0.

2. i = i + 1.

3. Если i n, то переход на п. (4), иначе если стек пуст, то выдаем сообщение “скобки сбалансированы”, в противном случае выдаем сообщение “скобки не сбалансированы”. Конец алгоритма.

4. Если i-й символ отличен от символов скобок, то переход на п. (2).

5. Если i-й символ равен “(” или “[”, то помещаем его в стек, переход на п. (2).

6. Если i-й символ равен “)”, то проверяем вершину стека: если в вершине стека находится “(”, то извлекаем ее из стека; переход на п. (2), иначе выдаем сообщение “скобки не сбалансированы”. Конец алгоритма.

7. Если i-й символ равен “]”, то проверяем вершину стека: если в вершине стека находится “[”, то извлекаем ее из стека; переход на п. (2), иначе выдаем сообщение “скобки не сбалансированы”. Конец алгоритма.

Очередь — частный случай линейного односвязного списка, для которого разрешены только две операции: добавление элемента в конец (хвост) очереди и удаление элемента из начала (головы) очереди.

Понятие очереди действительно очень близко к бытовому термину “очередь”. Очередь покупателей в магазине хорошо описывается в терминах этой структуры данных.

Деревья

Дерево — это совокупность элементов, называемых узлами, в которой выделен один элемент (корень), а остальные элементы разбиты на непересекающиеся множества (поддеревья), каждое из которых является деревом, при этом корень каждого поддерева является потомком корня дерева, т.е. все элементы связаны между собой отношением (предок–потомок). В результате образуется иерархическая структура узлов. Узлы, которые не имеют ни одного потомка, называются листьями. Над деревом определены следующие операции: добавление элемента в дерево, удаление элемента из дерева, обход дерева, поиск элемента в дереве.

Пример 4. Дерево является наиболее удобной структурой данных для представления генеалогического дерева, с помощью которого можно решать задачи определения степени родства между двумя людьми.

Используются деревья и для определения выигрышной стратегии в играх (см. статью “Игры. Выигрышные стратегии”), и для построения различных информационных моделей (см. “Информационные модели”).

Особенно важную роль в информатике играют так называемые бинарные деревья.

Двоичное (бинарное) дерево — частный случай дерева, в котором каждый узел может иметь не более двух потомков, являющихся корнями левого и правого поддерева.

Если дополнительно для узлов дерева выполняется условие, что все значения элементов левого поддерева меньше значения корня дерева, а все значения элементов правого поддерева больше значения корня, то такое дерево называется деревом бинарного поиска и предназначено для быстрого поиска элементов. Алгоритм поиска в таком дереве работает так: искомое значение сравнивается со значением корня дерева, и в зависимости от результата сравнения поиск либо заканчивается, либо продолжается только в левом или только в правом поддереве соответственно. Общее количество операций сравнения не будет превосходить так называемую высоту дерева — максимальное количество элементов на пути от корня дерева к одному из листьев. Так, высота изображенного на рисунке дерева равна 4.

Граф — это множество элементов, называемых вершинами графа вместе с набором отношений между этими вершинами, называемых ребрами графа. Графической интерпретацией этой структуры данных является множество точек, соответствующих вершинам, некоторые пары из которых соединены линиями или стрелками, которые соответствуют ребрам. В последнем случае граф называется ориентированным (см. также статьи “Графические модели” и “Табличные модели”).

В силу того, что с помощью графов можно описывать объекты произвольной структуры, графы являются основным средством для описания структур сложных объектов и функционирования систем. Например, для описания вычислительной сети, транспортной системы, иерархической структуры (дерево является одной из разновидностей графа). Блок-схемы алгоритмов (см. “Способы записи алгоритмов”) также представляют собой графы.

Если каждому ребру к тому же приписано некоторое число (вес), то такой граф называют взвешенным. Например, при описании с помощью графа системы дорог России важным является длина дороги (вес ребра графа), соединяющей те или иные населенные пункты (вершины графа). При этом на рисунке длины соответствующих ребер не обязаны соответствовать приписанным им весам, в отличие от карты дорог.

Пример 5. В терминах взвешенного графа удобно решать следующую задачу. Правительство России составляет план строительства современных автомагистралей, соединяющих города, население которых превышает миллион человек. Какие именно дороги следует построить, чтобы из любого такого города можно было добраться в любой другой по новым автомагистралям, а общая длина дорог была бы минимальной?

Эта задача в теории графов имеет простое и точное решение. Мы можем начать планирование сети дорог, начиная с любого города, например, Санкт-Петербурга. Соединим его с ближайшим городом-миллионником. Далее на каждом шаге к имеющейся сети добавляется кратчайшая дорога, которой можно соединить город, еще не присоединенный к сети, с одним из городов, уже включенных в сеть. Количество дорог будет, таким образом, на единицу меньше, чем число городов.

Абстрактную структуру данных — граф — в программе можно представить несколькими способами, т.е. используя разные типы данных. Например, граф можно описывать с помощью списка ребер, задавая каждое ребро парой вершин и, при необходимости, весом. Наибольшее распространение получило табличное хранение графа (см. “Табличные модели”), называемое также матрицей смежности, т.е. двухмерного массива, скажем, A, где для невзвешенного графа (или 1), если ребро между вершинами i и j существует, и (или 0) в противном случае. Для взвешенного графа A[i][j] равно весу соответствующего ребра, а отсутствие ребра в ряде задач удобно обозначать бесконечностью. Для неориентированных графов матрица смежности всегда симметрична относительно главной диагонали (i = j). C помощью матрицы смежности легко проверить, существует ли в графе ребро, соединяющее вершину i с вершиной j. Основной же ее недостаток заключается в том, что матрица смежности требует, чтобы объем памяти был достаточен для хранения N² значений для графа, содержащего N вершин, даже если ребер в графе существенно меньше, чем N².

Методические рекомендации

При объяснении понятия структуры данных можно воспользоваться следующей иллюстрацией.

При решении любой задачи возникает необходимость работы с данными и выполнения операций над ними. Набор этих операций для каждой задачи, вообще говоря, свой. Однако, если некоторый набор операций часто используется при решении различных задач, то полезно придумать способ организации данных, позволяющий выполнять именно эти операции как можно эффективнее. После того, как такой способ придуман, при решении конкретной задачи можно считать, что у нас в наличии имеется “черный ящик” (его мы и будем называть структурой данных), про который известно, что в нем хранятся данные некоторого рода, и который умеет выполнять некоторые операции над этими данными. Это позволяет отвлечься от деталей и сосредоточиться на характерных особенностях задачи. Внутри (т.е. в компьютере) этот “черный ящик” может быть реализован различным образом, при этом следует стремиться к как можно более эффективной (быстрой и экономично расходующей память) реализации.

Государственный образовательный стандарт предусматривает изучение различных структур данных как в базовом курсе основной школы, так и в старших классах. В курсе программирования основной школы в Примерной программе упоминаются в качестве обрабатываемых объектов цепочки символов (строки), числа, списки, деревья, графы. Однако в практических работах из данных сложной структуры упоминается только массив (см. статью “Операции с массивами”). В основной школе остальные структуры, видимо, имеет смысл изучать в первую очередь при построении графических и других моделей (см. раздел IV энциклопедии).

Примерная программа для профильной школы предполагает работу с числами, матрицами, строками, списками, деревьями. В качестве простой иллюстрации работы со списками можно выбрать организацию стека с помощью одномерного массива и целочисленной переменной, указывающей на вершину стека (“дно” стека при этом всегда находится в первом элементе массива). Помимо приведенной в статье задачи проверки скобок на сбалансированность, можно изучить работу стекового калькулятора на примере алгоритма перевода арифметического выражения в обратную польскую запись (постфиксную запись) из привычной нам инфиксной записи и дальнейшее вычисление значения арифметического выражения.

Бинарное дерево также легко представить в памяти компьютера с помощью одномерного массива, при этом в первом элементе массива будет храниться корень дерева, а потомки узла дерева, хранящегося в i-м элементе массива, будут располагаться в 2i-м и (2i + 1)-м элементах соответственно. Если потомок у узла отсутствует, то соответствующий элемент будет равен, например, 0. Рекурсивная процедура обхода дерева t и печати его элементов в этом случае будет выглядеть так:

procedure order(i:integer);

begin

if t[i] <> 0 then

begin

writeln(t[i]);

order(2*i);

order(2*i + 1)

end

end;

О реализации списков и массивов с помощью динамических переменных можно прочитать, например, в классической книге Н.Вирта “Алгоритмы и структуры данных”.

В программу для профильной школы включены и алгоритмы на графах. В частности, упоминается поиск кратчайшего пути в графе. Для невзвешенного графа решать эту задачу можно, например, с использованием алгоритма “поиска в ширину”, когда сначала помечаются вершины графа, соединенные ребром с исходной вершиной, затем все вершины, соединенные с помеченными, и т.д. Для взвешенного графа чаще всего используют алгоритм Дийкстры (см., например, статью Е.В. Андреевой “Олимпиады по информатике. Пути к вершине”, “Информатика” № 8/2002). Знание таких алгоритмов необходимо для успешного решения олимпиадных задач по информатике. Так, на IV федеральном окружном этапе Всероссийской олимпиады по информатике 2007 г. предлагалась задача “Окопы и траншеи”, решение которой как раз и сводилось к поиску кратчайшего пути во взвешенном графе.

16. Теория алгоритмов

Теория алгоритмов как раздел математики возникла в начале 30-х годов XX столетия в связи с необходимостью уточнения понятия алгоритма. Ранее, решая различные задачи, математики использовали интуитивное понятие алгоритма (см. статью “Алгоритм”). Но в связи с усложнением ставящихся задач у математиков стала возникать мысль, что не для всех задач можно найти процедуру решения, которая являлась бы алгоритмом, что впоследствии подтвердилось получением результатов о существовании алгоритмически неразрешимых проблем. Для доказательства факта отсутствия алгоритма необходимо было дать точное определение алгоритма. Ведь одно дело найти разрешающий алгоритм — это можно сделать, используя интуитивное понятие алгоритма. Другое дело — доказать несуществование алгоритма, для этого нужно знать точно, отсутствие чего мы доказываем. Попытки сформулировать такое определение привели в рамках математической логики к возникновению теории алгоритмов.

В теории алгоритмов используются различные подходы к формализации понятий алгоритма и вычислимой функции. Поиск таких подходов проходил в трех направлениях. В первом всякий алгоритм вычисляет значение некоторой числовой функции, а его элементарные шаги — это арифметические операции. Последовательность шагов определяется с помощью суперпозиции — подстановки функций в функции, рекурсии — определения значения функции через ранее вычисленные значения этой же функции, и оператора минимизации, благодаря которому из всюду определенной функции можно получить не всюду определенную вычислимую функцию. Класс функций, порождаемый этими тремя операторами, называется классом частично-рекурсивных функций. Второе направление основано на определении алгоритмического процесса как процесса, осуществимого на конкретной теоретической машине. Примерами таких алгоритмических моделей являются “машина Тьюринга” и “машина Поста”. Третье направление отвлекается от конкретных машин (т.е. в этих моделях отсутствуют понятия “память”, “состояние машины” и т.п.). Наиболее известная алгоритмическая модель этого типа — нормальные алгоритмы Маркова.

Все эти подходы привели к одному и тому же классу алгоритмически вычислимых функций. Указанные результаты составляют основу так называемой дескриптивной теории алгоритмов, основным содержанием которой является классификация задач по признаку алгоритмической разрешимости, т.е. получение высказываний типа “Задача П алгоритмически разрешима” или “Задача П алгоритмически неразрешима” (см. статью “Алгоритмически неразрешимые проблемы”). В данном направлении получен ряд фундаментальных результатов. Среди них доказательство Ю.В. Матиясевичем в 1970 году алгоритмической неразрешимости знаменитой десятой проблемы Гильберта.

Применение теории алгоритмов осуществляется как в использовании самих результатов (особенно это касается использования разработанных алгоритмов), так и в обнаружении новых понятий и уточнении старых. С ее помощью исследуются доказуемость, эффективность, разрешимость и др. Всякому алгоритму соответствует задача, для решения которой он предназначен. В обратную сторону это неверно — задача может решаться различными алгоритмами. Тем не менее задача определения эквивалентности двух алгоритмов является алгоритмически неразрешимой.

Применение ЭВМ послужило стимулом развития теории алгоритмов и изучения алгоритмических моделей, самостоятельного изучения алгоритмов с целью их сравнения по рабочим характеристикам (числу действий, расходу памяти), а также их оптимизации. Возникло важное направление в теории алгоритмов — сложность алгоритмов и вычислений. Начала складываться так называемая метрическая теория алгоритмов, основным содержанием которой является классификация задач по классам сложности. Сами алгоритмы стали объектом точного исследования, как и те объекты, для работы с которыми они предназначены.

Формальное определение алгоритма и вычисление функции*

Все задачи принято делить на два класса: задачи, связанные с вычислением функций, и задачи, связанные с распознаванием принадлежности объекта заданному множеству (или ответом на вопрос: обладает ли объект заданным свойством?). В первом случае алгоритм A вычисляет функцию f_A, т.е., начав работать с входными данными x, он должен через некоторое время остановиться и выдать результат y = f_A(x). Функция f_A не обязательно числовая. Например, функция “телефонный справочник” может по фамилии абонента выдать его телефонный номер. Алгоритм вычисления этой функции заключается в поиске нужной фамилии в упорядоченном по алфавиту списке абонентов. Во втором случае алгоритм отвечает на вопрос: “Истинно ли высказывание x M?” — и выдает один из двух возможных результатов: да или нет. Мы также можем считать это функцией, принимающей два значения. Многие практические задачи включают в себя оба случая. Например, при решении квадратного уравнения сначала нужно выяснить вопрос о существовании действительных корней уравнения, и только при положительном ответе на этот вопрос вычисляются корни. Первое из понятий приводит к так называемым вычислимым функциям.

Теория вычислимых функций появилась в 1930-е годы благодаря усилиям нескольких авторов почти одновременно (под разными названиями). Возникли понятия общерекурсивной функции, -определимой функции (Черч: 1933 г., Клини: 1935 г.), вычислимой функции по Тьюрингу (Тьюринг: 1936 г., 1937 г.), представимой функции в формальной системе (Гедель: 1936 г.), комбинаторно определимой функции (Шейнфинкель, Карри, Россер: 1924–1936 гг.), а также понятия канонической системы (Пост: 1943 г.), нормального алгоритма (Марков: 1950 г.).

При всех известных подходах к формализации понятия вычислимости сначала вводится в рассмотрение множество конструктивных объектов, которые в конечном счете могут быть представлены словами конечной длины в конечном алфавите. В частности, конструктивными являются конечные натуральные числа, которые можно трактовать как слова в алфавите “0”..”9”.

Функция f с натуральными аргументами и значениями называется вычислимой, если существует алгоритм, ее вычисляющий, то есть такой алгоритм A, что

· если f(n) определено для какого-либо натурального n, то алгоритм A, получая на вход n, останавливается и печатает f_A(n) = f(n);

· если f(n) не определено, то алгоритм A не останавливается, получив на входе n, т.е. f_A(n) не определено.

Понятие вычислимости определяется здесь для частичных функций (областью определения которых является некоторое подмножество натурального ряда). Например, нигде не определенная функция вычислима (в качестве A надо взять программу, которая всегда зацикливается).

Любые конструктивные объекты реального мира также можно изображать словами в различных конечных алфавитах. Это позволяет считать, что объектами работы алгоритмов могут быть только слова. Слово, которое подается на вход алгоритма, называется входным словом; слово, получаемое в результате работы алгоритма, называется выходным. Совокупность слов, к которым применим алгоритм, называется областью применимости алгоритма.

Алан Матисон Тьюринг
(Alan Mathison Turing)

Утверждение о том, что та или иная алгоритмическая модель универсальна, означает, что для любой вычислимой функции существует алгоритм, описываемый средствами этой модели. В теории алгоритмов была доказана равносильность всех известных формализаций понятия алгоритма.

До сих пор неизвестно ни одного алгоритма из числа алгоритмов, изобретенных человечеством за свою многотысячелетнюю историю, который не был бы эквивалентен ни одному из формализованных алгоритмов (например, алгоритму Маркова, машине Тьюринга или частично рекурсивной функции — функции, не являющейся всюду определенной).

Андрей Андреевич Марков

Оказалось, что все эти понятия эквивалентны между собой и каждое из них можно рассматривать в качестве одного из способов точного определения понятия алгоритма.

Машина Тьюринга и Поста

Машиной Тьюринга (МТ) называется упорядоченный набор вида {A, a₀, Q, q₁, q₀, T, }, где

A — конечное множество, называемое основным алфавитом МТ,

a₀ A и называется пустой буквой алфавита,

Q — конечное множество, называемое алфавитом состояний МТ,

q₁ Q — начальное состояние МТ,

q₀ Q — заключительное, или состояние останова МТ,

T = {Л, Н, П} — множество сдвигов МТ,

t — программа МТ, то есть

.: A x Q \ {q₀} A x T x Q

Нетрудно убедиться, что в этом определении фигурируют только математические и логические термины (или символы), например, множество, конечное множество, элемент множества, принадлежность множеству, произведение множеств.

Для любого наугад взятого алгоритма, работающего не над словами, его объекты можно закодировать так, что они становятся словами в некотором алфавите, а суть алгоритма от этого не меняется.

Что же представляет собой машина Тьюринга? В каждой машине Тьюринга есть две части:

1) неограниченная в обе стороны лента, разделенная на ячейки;

2) головка для считывания/записи, управляемая программой.

С каждой машиной Тьюринга связаны два конечных алфавита: алфавит входных символов A = {a₁, a₂, …, a_m}и алфавит состояний  Q = {q₁, q₂, …, q_m}. (С разными машинами Тьюринга могут быть связаны разные алфавиты A и Q.) Состояние q₀ называется заключительным, или состоянием останова. Считается, что если машина попала в это состояние, то она заканчивает свою работу. Состояние называется начальным. Находясь в этом состоянии, машина начинает свою работу.

Входное слово размещается на ленте по одной букве в расположенных подряд ячейках. Слева и справа от входного слова находятся только пустые ячейки (в алфавит А всегда входит “пустая” буква а₀ — признак того, что ячейка пуста).

Автомат может двигаться вдоль ленты влево или вправо, читать содержимое ячеек и записывать в ячейки буквы своего алфавита. Ниже схематично нарисована машина Тьюринга, автомат которой обозревает первую ячейку с данными.

Автомат каждый раз “видит” только одну ячейку. В зависимости от того, какую букву он видит, а также в зависимости от своего состояния , автомат может выполнять следующие действия:

· записать новую букву в обозреваемую ячейку;

· выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться неподвижным;

· перейти в новое состояние.

Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.

Клетка (q_j, a_i) определяется двумя параметрами — символом алфавита и состоянием машины. Команда представляет собой указание: какой символ записать в текущую ячейку, куда передвинуть головку чтения/записи, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: “Л” (влево), “П” (вправо) или “Н” (неподвижен).

После выполнения очередной команды МТ переходит в состояние q_k (которое может в частном случае совпадать с прежним состоянием q_j). Следующую команду нужно искать в k-й строке таблицы на пересечении со столбцом, соответствующим букве, которую автомат видит после сдвига. В процессе работы автомат перескакивает из одной клетки программы, записанной в виде таблицы, в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние q₀, т.е. остановиться. Будем говорить, что такие клетки содержат команду останова.

Если клеток останова в программе вообще нет или в процессе работы над входным словом МТ никогда не окажется в заключительном состоянии, то считается, что машина Тьюринга неприменима к данному входному слову. Машина Тьюринга применима к входному слову только в том случае, если, начав работу над этим входным словом, она окажется в заключительном состоянии.

Пример. Пусть требуется построить машину Тьюринга, которая прибавляет единицу к числу на ленте. Входное слово состоит из цифр целого десятичного числа, записанных в последовательные ячейки на ленте. В начальный момент машина находится против самой правой цифры числа.

Решение. Машина должна прибавить единицу к последней цифре числа. Если последняя цифра равна 9, то ее заменить на 0 и прибавить единицу к предыдущей цифре. Программа для данной машины Тьюринга может выглядеть так:

Тезис Тьюринга состоит в том, что всякий алгоритм может быть реализован соответствующей машиной Тьюринга. Тезис Тьюринга является основной нематематической гипотезой теории алгоритмов, понимаемых по Тьюрингу. Одновременно этот тезис приводит к формальному определению алгоритма.

Алгоритм (по Тьюрингу) — программа для машины Тьюринга, приводящая к решению поставленной задачи.

В статье “Исполнители алгоритмов” 2 говорилось, что у каждого исполнителя есть своя система команд, свой круг задач. Тьюрингом же был описан универсальный исполнитель — машина Тьюринга, этот исполнитель способен решить любую алгоритмически разрешимую задачу. Этот фундаментальный результат был получен в то время, когда универсальных вычислительных машин еще не существовало. Более того, сам факт математического построения воображаемого универсального исполнителя позволил высказать предположение о целесообразности построения универсальной вычислительной машины, которая бы могла решать любые задачи при условии соответствующей кодировки исходных данных и разработки соответствующей программы действий исполнителя.

Почти одновременно с А.Тьюрингом (1937 г.) американский математик Эмиль Пост предложил иную абстрактную машину, характеризующуюся еще большей простотой, чем машина Тьюринга. Это строгое математическое построение было также предложено в качестве уточнения понятия алгоритма.

Эмиль Леон Пост
(Emil Leon Post)

В машине Поста в ячейках бесконечной ленты можно записывать всего два знака: 0 и 1 (ставить метку в ячейку или стирать метку). Это ограничение не влияет на ее универсальность, так как любой алфавит может быть закодирован двумя знаками. Кроме ленты, в машине Поста имеется каретка (головка чтения/записи), которая:

· умеет двигаться вперед, назад и стоять на месте;

· умеет читать содержимое, стирать и записывать 0 или 1;

· управляется программой.

Как и машина Тьюринга, машина Поста может находиться в различных состояниях, но каждому состоянию соответствует не строка состояния с клетками, а некоторая команда одного из следующих шести типов (все строки в программе пронумерованы):

1. Записать 1 (метку), перейти к i-й строке программы;

2. Записать 0 (стереть метку), перейти к i-й строке программы;

3. Сдвиг влево, перейти к i-й строке программы i;

4. Сдвиг вправо, перейти к i-й строке программы;

5. Останов;

6. Если 0, то перейти к i, иначе перейти к j.

Состояние машины — это состояние ленты и положение головки чтения/записи. Тезис Поста заключается в том, что: “Всякий алгоритм представим в форме машины Поста”. Отсюда следует другое формальное определение алгоритма.

Алгоритм (по Посту) — программа для машины Поста, приводящая к решению поставленной задачи. Тезис Поста невозможно строго доказать, так же, как и тезис Тьюринга.

Как уже говорилось выше, в теории алгоритмов доказано, что машина Поста и машина Тьюринга эквивалентны по своим возможностям. Более того, для каждого неформализованного алгоритма A существует формализованный алгоритм B (например, машина Тьюринга). В этом состоит полнота формализации понятия вычислимой функции.

Универсальная функция

В теории алгоритмов установлен важный факт: во всех алгоритмических моделях всегда существует универсальный алгоритм, т.е. алгоритм, который способен моделировать работу любого другого алгоритма, описанного в этой же модели. Покажем существование универсальной функции для вычислимых функций одного аргумента.

Теорема. Существует вычислимая функция двух аргументов U, являющаяся универсальной функцией для класса вычислимых функций одного аргумента.

Алгоритм, вычисляющий саму функцию U, есть, по существу, интерпретатор для используемого языка программирования (если отождествлять программу и ее номер, то он применяет первый аргумент ко второму).

Аналогично можно ввести универсальные функции для произвольного числа аргументов. Концепция универсального алгоритма еще в 30-е годы XX века показала возможность создания универсального устройства (компьютера), способного выполнять любые алгоритмы.

Индуктивное определение объектов**

В одной из наиболее общих форм индуктивное определение какого-либо класса (множества) объектов K осуществляется по следующей схеме. 1) Задается класс исходных (атомарных, простейших) объектов A определяемого класса K [Базис индуктивного определения].) Задается система правил R, позволяющих из уже определенных (или построенных, порожденных) объектов получать (строить, порождать) новые объекты определяемого класса K [Шаг индуктивного определения]. 3) Объектами определяемого класса K считаются те и только те объекты, которые могут быть получены (построены, порождены) согласно пунктам 1) и) этого определения. При этом пункт 3) данного определения часто только подразумевается, но не формулируется явно.

С приведенным выше индуктивным определением класса объектов связан обобщенный принцип индукции (называемый также индукцией по построению объектов), который состоит в следующем. Для того чтобы доказать, что любой объект из класса, задаваемого данным индуктивным определением, обладает каким-либо свойством P, достаточно доказать, во-первых, что каждый исходный (атомарный, простейший) объект, задаваемый пунктом 1) данного индуктивного определения, обладает этим свойством P [Базис индукции], и, во-вторых, что этим свойством P будет обладать любой объект, который может быть получен (построен, порожден) по какому-либо правилу пункта) данного индуктивного определения, из объектов, уже обладающих этим свойством P [Шаг индукции].

Пример 1. Индуктивное определение класса высказывательных формул, принятое в математической логике (см. “Логические выражения”).

Мы предполагаем, что нам дано множество высказывательных переменных: p₁, p₂, ..., p_n, ... , а также символы логических операций: (конъюнкция), (дизъюнкция), (импликация), (эквивалентность), (отрицание). Теперь мы даем следующее индуктивное определение:

1) Высказывательные переменные: p₁, p₂, ..., p_n, ... считаются формулами (атомарными формулами) [Базис индуктивного определения].

2) Если и какие-то уже построенные высказывательные формулы, то формальные выражения — также высказывательные формулы.

3) Высказывательными формулами считаются те и только те формальные выражения, которые могут быть построены согласно пунктам 1) и) этого определения.

Пример 2. Индуктивное определение класса термов (говоря нестрого, терм — это формальный аналог имени существительного).

Мы предполагаем, что нам даны попарно непересекающиеся множества:

1) множество предметных переменных: x₁, x₂, ..., x_n, ... ,

2) множество предметных констант: c₁, c₂, ..., c_n, ... , а также

3) для каждого целого положительного n нам дано множество символов n-местных функций f₁ⁿ, f₂ⁿ, ..., f_kⁿ, ... ,.

Теперь мы даем следующее индуктивное определение класса термов.

1) Предметные переменные x₁, x₂, ..., x_n, ... и предметные константы c₁, c₂, ..., c_n, ...  считаются термами (и притом атомарными термами) [Базис индуктивного определения].

2) Для любых целых положительных чисел n и k, если t₁, t₂, ..., t_n — какие-либо n уже построенных термов, то формальное выражение f_kⁿ(t₁, t₂, ..., t_n ) также является термом.

3) Термами считаются те и только те формальные выражения, которые могут быть получены (построены, порождены) согласно пунктам 1) и) этого определения.

Это определение используется, в частности, для построения грамматик различных языков программирования (см. “Языки программирования”).

Сложность алгоритма

Сложность алгоритма — это количественная характеристика, которая говорит либо о том, сколько времени он работает (временная или вычислительная сложность), либо о том, какой объем памяти он использует. Вычислительным процессом, порожденным алгоритмом, называется последовательность шагов алгоритма, пройденных при исполнении этого алгоритма.

Вычислительная сложность алгоритма — количество элементарных шагов в вычислительном процессе этого алгоритма. Обратите внимание: именно в вычислительном процессе, а не в самом алгоритме. Очевидно, для сравнения сложности разных алгоритмов необходимо, чтобы сложность подсчитывалась в одних и тех же элементарных действиях.

Временная сложность алгоритма — это время Т, необходимое для его выполнения. Оно равно произведению числа элементарных действий на среднее время выполнения одного действия: Т = kt. Поскольку t зависит от исполнителя, реализующего алгоритм, то естественно считать, что сложность алгоритма в первую очередь зависит от k. Очевидно, что в наибольшей степени количество операций при выполнении алгоритма зависит от количества обрабатываемых данных. Действительно, для упорядочивания по алфавиту списка из 100 фамилий требуется существенно меньше операций, чем для упорядочивания списка из 100 000 фамилий. Поэтому сложность алгоритма выражают в виде функции от объема входных данных. Пусть есть алгоритм А. Для него существует параметр n, характеризующий объем обрабатываемых алгоритмом данных, этот параметр часто называют размерностью задачи. Обозначим через T(n) время выполнения алгоритма, через f — некую функцию от n.

Будем говорить, что T(n) алгоритма имеет порядок роста f(n) при n , или, по-другому, алгоритм имеет теоретическую сложность O(f(n)) (читается “о большое от f(n)”), если найдется такая константа с > 0 и число n₀, что T(n) сf(n) при всех n n0. Здесь предполагается, что f(n) неотрицательно, по крайней мере при n n0.

Так, например, алгоритм, выполняющий только операции чтения данных и занесения их в оперативную память, имеет линейную сложность O(n). Алгоритм сортировки методом “пузырька” (см. “Операции с массивами”) имеет квадратичную сложность O(n²), так как при сортировке любого массива надо выполнить (n² - n)/2 операций сравнения (при этом операций перестановок вообще может не быть, например, на упорядоченном массиве).

Для решения задачи могут быть разработаны алгоритмы различной сложности. Логично воспользоваться лучшим среди них, т.е. имеющим наименьшую сложность.

Сложность алгоритма по памяти определяется числом ячеек памяти, используемых в процессе его работы. Число шагов алгоритма может сколь угодно сильно превосходить объем памяти за счет циклов по одним и тем же объектам. Поэтому временная сложность считается основной характеристикой алгоритма.

Методические рекомендации

Материал данной темы носит теоретический характер и достаточно сложен для понимания. Он включен в Стандарт профильной школы. Цель раскрытия данной темы — проследить вместе со школьниками цепочку

формальное определение алгоритма алгоритмически неразрешимые задачи вычислимые функции универсальный исполнитель

Проще всего объяснить школьникам формальное определение алгоритма можно с помощью машины Поста или машины Тьюринга. Полезно рассмотреть и примеры решения задач с помощью одной из этих машин. Программирование машины Поста учащимся дается легче, чем программирование машины Тьюринга. Во-первых, это связано с тем, что все действия, выполняемые машиной Поста, прописаны в командах, которые выполняются в привычном нам порядке (последовательное выполнение + условный переход) (не надо блуждать по таблице-программе машины Тьюринга). В пользу машины Поста говорит простота ее описания (хотя многие задачи в силу ограниченных возможностей машины по сравнению с машиной Тьюринга решать становится сложнее), а в пользу машины Тьюринга — то, что на ее примере учащиеся могут познакомиться с таким новым для них и очень важным понятием, как конечный автомат.

Полезным может оказаться и выполнение упражнений на индуктивное определение объектов. Зачастую это единственный способ достаточно просто описать не только весьма непростые вещи, такие, как грамматика языка программирования, но и арифметические или логические выражения. Индуктивные определения объектов непосредственно связаны с рекурсивными описаниями подпрограмм в языках программирования.

В теории алгоритмов важным является и следующий факт: в любой алгоритмической модели всегда существует универсальная вычислимая функция, т.е. алгоритм, который способен моделировать работу любого другого алгоритма, описанного в этой же модели. Этот результат, установленный еще в 30-е годы прошлого века, показывает, что в основе работы компьютера как универсального вычислителя лежат не только физические, но и математические принципы.

После введения точного определения алгоритма в разных областях математики стали обнаруживать алгоритмически неразрешимые проблемы. Знание примеров неразрешимостей предостерегает от увлечения глобальными проектами всеобщей алгоритмизации точно так же, как знание основных законов физики предостерегает от попытки создать вечный двигатель.

Понятие сложности алгоритма позволяет сравнивать алгоритмы между собой, а также ставит проблему решения так называемых “переборных задач”, число действий в алгоритме решения которых выражается так называемой “экспоненциальной функцией”, например, 2ⁿ, n! или даже nⁿ. Использование таких алгоритмов возможно лишь для маленьких значений n (приблизительно 20, 10 и 7 для приведенных функций для 1 секунды работы современного персонального компьютера). Причем увеличение производительности компьютера или времени счета в 100 раз приводит к увеличению возможной размерности задачи приблизительно на 7, 2 и 2 соответственно. То есть для больших размерностей такие алгоритмы не только не применимы сейчас, но и не будут применимы в обозримом будущем.

17. Типы данных

Информация, поступающая в компьютер, состоит из определенного множества данных, относящихся к какой-то проблеме, — это именно те данные, которые относятся к конкретной задаче и из которых требуется получить желаемый ответ. В математике классифицируют данные в соответствии с некоторыми важными характеристиками. Принято различать целые, вещественные и логические данные, множества, последовательности, векторы, матрицы (таблицы) и т.д. В обработке данных на компьютере классификация играет даже боRльшую роль.

Любая константа, переменная, выражение или функция относятся к некоторому типу. Тип данных определяет диапазон допустимых значений и операций, которые могут быть применены к этим значениям. Кроме того, тип данных задает формат представления объектов в памяти компьютера, ведь в конце концов любые данные будут представлены в виде последовательности двоичных цифр (нулей и единиц). Тип данных указывает, каким образом следует интерпретировать эту информацию. Тип любой величины может быть установлен при ее описании, а в некоторых языках может выводиться компилятором по ее виду (Fortran, Basic).

Например, если переменная имеет целочисленный тип данных, то таким образом определен диапазон значений, которые могут быть сохранены в этой переменной (целые числа) и определены операции, которые могут быть применены к этой переменной (арифметические, логические, возможность ввода и вывода значений этой переменной). Каждый язык программирования поддерживает один или несколько типов данных. Наличие в языке программирования типизации означает жесткую связку операций и типов объектов, над которыми их можно выполнять. Не все языки обладают таким свойством. Например, в языке С практически любые операции можно выполнять над любыми данными (например, складывать два символа или число с логическим значением, но в большинстве случаев такие операции бессмысленны и соответствуют ошибке в программе, на которую компилятор указать не сможет).

Классификация типов данных

Любые данные могут быть отнесены к одному из двух типов: простому (основному), форма представления которого определяется архитектурой ЭВМ, или сложному, конструируемому пользователем для решения конкретных задач. Данные простого типа — это символы, числа и т.п. элементы, дальнейшее дробление которых не имеет смысла. Из таких элементарных данных формируются структуры (сложные типы) данных.

Принято различать следующие типы данных:

· Простые.

o Числовые типы.

§ Целочисленные.

§ Вещественные.

o Символьный тип.

o Логический тип.

o Перечислимый тип.

o Множество.

o Указатель.

· Составные.

o Массив.

o Строковый тип.

o Запись.

o Последовательность.

Рассмотрим перечисленные типы данных подробнее.

Числовые типы. Значениями переменных таких типов являются числа. К ним могут применяться обычные арифметические операции, операции сравнения (в результате получается логическое значение). Принципиально различны в компьютерном представлении целые и вещественные типы.

Целочисленные типы данных делятся, в свою очередь, на знаковые и беззнаковые. Целочисленные со знаком могут принимать как положительные, так и отрицательные значения, а беззнаковые — только неотрицательные значения. Диапазон значений при этом определяется количеством разрядов, отводимых на представление конкретного типа в памяти компьютера (см. “Представление чисел”).

Вещественные типы бывают: с фиксированной точкой, то есть хранятся знак и цифры целой и дробной частей (в настоящее время в языках программирования реализуются редко), и с плавающей точкой, то есть число приводится к виду m х 2^e, где m — мантисса, а e — порядок числа, причем 1/2 m 1, e — целое число. В данном случае хранятся знак, число e и двоичные цифры дробной части числа m, которые умещаются в отведенную для этого память. Говорят, что вещественные числа представимы с некоторой точностью.

Символьный тип. Элемент этого типа хранит один символ. При этом могут использоваться различные кодировки, которые определяют, какому коду (двоичному числу) какой символ (знак) соответствует. К значениям этого типа могут применяться операции сравнения (в результате получается логическое значение). Символы считаются упорядоченными согласно своим кодам (номерам в кодовой таблице).

Логический тип. Данные этого типа имеют два значения: истина (true) и ложь (false). К ним могут применяться логические операции. Используется в условных выражениях, операторах ветвления и циклах. В некоторых языках, например С, является подтипом числового типа, при этом ложь = 0, истина = 1 (или истинным считается любое значение, отличное от нуля).

Перечислимый тип. Отражает самый прямолинейный способ описания простого типа — перечисление всех значений, относящихся к этому типу. Каждая константа такого типа получает свой порядковый номер, что позволяет реализовать ряд простых операций над этим типом, таких, как получить следующее по порядку значение данного типа.

Множество как тип данных в основном совпадает с обычным математическим понятием множества. Допустимы стандартные операции с множествами и проверка на принадлежность элемента множеству. В некоторых языках рассматривается как составной тип (массив логических значений, i-й элемент которого указывает, находится ли i в множестве), однако эффективней реализовывать множество как машинное слово (или несколько слов), каждый бит которого характеризует наличие соответствующего элемента в множестве.

Указатель (тип данных). Если описанные выше типы данных представляли какие-либо объекты реального мира, то указатели представляют объекты компьютерного мира, то есть являются исключительно компьютерными терминами. Переменная-указатель хранит адрес в памяти компьютера, указывающий на какую-либо информацию, как правило — на другую переменную.

Составные типы

Составные типы формируются на основе комбинаций простых типов.

Массив является индексированным набором элементов одного типа, простого или составного (см. “Операции с массивами”). Одномерный массив предназначен для компьютерной реализации такой структуры, как вектор, двухмерный массив — таблицы.

Строковый тип. Хранит строку символов. Вообще говоря, может рассматриваться как массив символов, но иногда рассматривается в качестве простого типа. Часто используется для хранения фамилий людей, названий предметов и т.п. К элементам этого типа может применяться операция конкатенации (сложения) строк. Обычно реализованы также операции сравнения над строками, в том числе операции “<” и “>”, которые интерпретируются как сравнение строк согласно алфавитному порядку (алфавитом здесь является набор символов соответствующей кодовой таблицы). Во многих языках реализованы и специальные операции над строками: поиск заданного символа (подстроки), вставка символа, удаление символа, замена символа.

Запись. Наиболее общий метод получения составных типов из простых заключается в объединении элементов произвольных типов. Причем сами эти элементы могут быть, в свою очередь, составными. Так, человек описывается с помощью нескольких различных характеристик, таких, как имя, фамилия, дата рождения, пол, и т.д. Записью (в языке С — структурой) называется набор различных элементов (полей записи), хранимый как единое целое. При этом возможен доступ к отдельным полям записи. К полю записи применимы те же операции, что и к базовому типу, к которому это поле относится (тип каждого поля указывается при описании записи).

Последовательность. Данный тип можно рассматривать как массив бесконечного размера (память для него может выделяться в процессе выполнения программы по мере роста последовательности). Зачастую такой тип данных обладает лишь последовательным доступом к элементам. Под этим подразумевается, что последовательность просматривается от одного элемента строго к следующему, формируется же она путем добавления элементов в ее конец. В языке Pascal подобному типу соответствуют файловые типы данных.

Преимущества от использования типов данных

Типы данных защищают программы по крайней мере от следующих ошибок:

1. Некорректное присваивание. Пусть переменная объявлена как имеющая числовой тип. Тогда попытка присвоить ей символьное или какое-либо другое значение приведет к ошибке еще на этапе компиляции. Такого рода ошибки трудно отследить обычными средствами.

2. Некорректная операция. Типизация позволяет избежать попыток применения выражений вида “Hello world” + 1. Поскольку, как уже говорилось, все переменные в памяти хранятся как наборы битов, то при отсутствии типов подобная операция была выполнима (и могла дать результат вроде “Hello worle”!). С использованием типов такие ошибки отсекаются опять же на этапе компиляции.

3. Некорректная передача параметров в процедуры и функции (см. “Подпрограммы”). Если функция “синус” ожидает, что ей будет передан числовой аргумент, то передача ей в качестве параметра строки “Hello world” может иметь непредсказуемые последствия. При помощи контроля типов такие ошибки также отсекаются на этапе компиляции или приводят к ошибкам выполнения программы, если значения параметра вводятся с клавиатуры или файла.

Кроме того, типы данных позволяют программисту абстрагироваться от машинного представления информации в виде наборов нулей и единиц и строить программы, основываясь на знакомых понятиях, таких, как числа, множества, последовательности, и т.п. В конечном итоге это приводит к получению более надежных программ.

Методические программы

При изучении данной темы самое главное — разделить следующие понятия:

данные — тип данных — абстрактная структура данных — структура данных

Типом данных переменной называют множество значений, которые может принимать эта переменная, и множество операций, которые применимы к этим значениям.

Абстрактная структура данных (см. “Структуры данных”) — это некоторая математическая модель данных (см. выше), включающая различные операции, определенные в рамках этой модели. Для реализации абстрактной структуры в том или ином языке программирования используются структуры, которые представляют собой набор переменных, возможно различных типов данных, объединенных определенным образом. При этом одна и та же абстрактная структура данных может быть реализована через различные структуры языка программирования. Например, такая абстрактная структура данных, как список, может быть реализована с использованием массива, файла или списка динамических переменных. Примеры различных структур данных, реализующих абстрактную структуру граф, приведены в статье “Табличные модели” 2.

Изучение конкретных типов данных производится в процессе рассмотрения определенного языка программирования в курсе информатики. При этом нельзя совсем не касаться таких вопросов, как представление определенного типа данных в памяти компьютера и диапазон значений, которые могут принимать переменные каждого из типов. Рассказывать стоит и о преобразованиях типов, как автоматических, выполняемых компилятором при анализе операции присваивания, например, вещественной переменной целочисленного выражения, так и производимых программистом, например, при переводе текстовой информации в числовую и т.д.

Изучение особенностей представления целых чисел (а именно этот тип данных встречается в учебных задачах по программированию чаще всего) полезно проиллюстрировать следующим примером.

Пример. С помощью программы на языке Borland Pascal вычислим значение n! (факториал числа n). Версия языка в данном случае указана потому, что ею определяется количество разрядов, отводимых на переменные определенного типа. В данном случае на переменные типа integer отводится 16 бит, что определяет диапазон значений этого знакового типа от –32 768 до 32 767.

var a,i,n: integer;

readln(n);

a := 1;

for i := 2 to n do

a := a * i;

writeln(a)

end.

При запуске этой программы для n = 7, 8 и 10 мы получим 5040, –25 216 и 24 320 соответственно. Первое полученное значение является верным, второе (отрицательное) может натолкнуть программиста на мысль, что в результате арифметических действий произошел выход за границу диапазона значений типа, а вот третье число само по себе может показаться верным, хотя, конечно, это не так.

На этом примере можно показать, что правильный алгоритм решения задачи при неправильном выборе типов данных может привести к абсурдному результату. И при разработке программы одним из важных этапов является оценка возможных значений (в том числе промежуточных) используемых переменных и выбор подходящих типов данных.

Следует подчеркнуть, что для целого типа выход за диапазон значений не приводит к прерыванию работы процессора (компьютер выдает неверные результаты), а для вещественных чисел (переполнение порядка) — это аварийная ситуация (floating point error), которая не пройдет незамеченной.

Язык программирования — искусственный (формальный) язык, предназначенный для записи программ для исполнителя (например, компьютера или станка с числовым управлением). Язык программирования задается своим описанием. Описание языка программирования — это документ, специфицирующий возможности алгоритмического языка. Обычно описание содержит:

· алфавит допустимых символов и служебных (ключевых) слов;

· синтаксические правила построения из алфавита допустимых конструкций языка;

· семантику, объясняющую смысл и назначение конструкций языка.

Языки программирования служат для представления решения задач в такой форме, чтобы они могли быть выполнены на ЭВМ.

Машинный язык, который состоит из команд процессора ЭВМ, также является языком программирования. Но алгоритмы, записанные на машинном языке, трудны для чтения даже программисту-разработчику, кроме того, работа с таким языком требует знания архитектуры конкретного компьютера, поэтому в программировании, как правило, используют языки более высокого уровня, чем машинные языки. Язык высокого уровня — это язык программирования, понятия и структура которого удобны для восприятия человеком и не зависят от конкретного компьютера, на котором будет выполняться программа.

Для того чтобы программу, записанную на языке программирования высокого уровня, можно было выполнить на компьютере, ее надо перевести на машинный язык. Программное средство, выполняющее эту функцию, называется транслятором.

Транслятор — это программа, которая считывает текст программы, написанной на одном языке, и транслирует (переводит) его в эквивалентный текст на другом языке (обычно на машинном языке). Трансляторы бывают двух основных видов: компиляторы и интерпретаторы.

Компилятор преобразует текст исходной программы в набор инструкций для данного типа процессора (машинный код) и далее записывает его в исполняемый файл (exe-файл), который может быть запущен на выполнение как отдельная программа. Другими словами, компилятор переводит программу с языка высокого уровня на низкоуровневый язык.

Интерпретатор в результате трансляции выполняет операции, указанные в исходной программе. При этом программа остается на исходном языке и не может быть запущена на выполнение без интерпретатора.

Разделение на компилируемые и интерпретируемые языки является несколько условным. Так, для любого традиционно компилируемого языка, как, например, Pascal, можно написать интерпретатор, а для любого интерпретируемого языка можно создать компилятор, — например, язык Бейсик, изначально интерпретируемый, может компилироваться без каких бы то ни было ограничений.

Некоторые языки, например Java и C#, находятся между компилируемыми и интерпретируемыми. А именно, программа компилируется не в машинный язык, а в машинно-независимый код низкого уровня, байт-код. Далее байт-код выполняется виртуальной машиной. Для выполнения байт-кода обычно используется интерпретация. Подобный подход в некотором смысле позволяет использовать плюсы как интерпретаторов, так и компиляторов.

Со времени создания первых программируемых машин человечество придумало уже более двух с половиной тысяч языков программирования. Количество языков программирования постоянно растет, хотя этот процесс явно замедлился. Некоторыми языками пользуется только небольшое число программистов, другие становятся известны миллионам людей. Часть из них узкоспециализированны (предназначены для решения определенного класса задач), а часть — универсальны. Профессиональные программисты иногда применяют в своей работе более десятка разных языков программирования.

Классификацию языков программирования можно вести по нескольким критериям: машинно-ориентированные (ассемблеры) и машинно-независимые, специализированные и универсальные.

К специализированным языкам можно отнести язык АРТ (Automatically Programmed Tools) — первый специализированный язык программирования для станков с числовым управлением. Язык был разработан группой американских специалистов в 1956–1959 гг. под руководством математика Дугласа Т. Росса. Язык СOBOL (Common Business–Oriented Language), созданный в США под руководством Грейс Мюррей Хоппер в 1959 г., ориентирован на обработку экономической информации. Математик Грейс Мюррей Хоппер возглавила проект по разработке СOBOL в чине капитана второго ранга, впоследствии она стана контр-адмиралом. Г.М. Хоппер называют “мамой и бабушкой” СOBOLа.

Грейс Мюррей Хоппер
(Grace Murray Hopper)

К специализированным языкам можно отнести и современные языки web-программирования Perl и PHP. Языки Рапира, Е-язык (Россия), SMR (Великобритания), LOGO (США) можно отнести к языкам, предназначенным для обучения программированию.

Самыми распространенными универсальными языками программирования сегодня являются C++, Delphi, Java, Pascal, Visual Basic, Python.

Но, рассматривая языки программирования как самостоятельный объект исследования, можно провести их классификацию по концепции построения языка.

Классификация языков программирования

Языки программирования можно разделить на два класса: процедурные и непроцедурные. Процедурные (императивные) языки — это языки операторного типа. Описание алгоритма на этом языке имеет вид последовательности операторов. Характерным для процедурного языка является наличие оператора присваивания (Basic, Pascal, С). Программа, написанная на императивном языке, очень похожа на приказы, выражаемые повелительным наклонением в естественных языках, то есть это последовательность команд, которые должен выполнить компьютер. Программируя в императивном стиле, программист должен объяснить компьютеру, как нужно решать задачу.

Непроцедурные (декларативные) языки — это языки, при использовании которых в программе в явном виде указывается, какими свойствами должен обладать результат, но не говорится, каким способом он должен быть получен. Непроцедурные языки делятся на две группы: функциональные и логические.

Декларативные языки программирования — это языки программирования высокого уровня, в которых операторы представляют собой объявления или высказывания в символьной логике. Типичным примером таких языков являются языки логического программирования (языки, основанные на системе правил и фактов). Характерной особенностью декларативных языков является их декларативная семантика. Основная концепция декларативной семантики заключается в том, что смысл каждого оператора не зависит от того, как этот оператор используется в программе. Декларативная семантика намного проще семантики императивных языков, что может рассматриваться как преимущество декларативных языков над императивными.

Логические языки

В программах на языках логического программирования соответствующие действия выполняются только при наличии необходимого разрешающего условия на вывод новых фактов из данных фактов согласно заданным логическим правилам. Логическое программирование основано на математической логике (см. “Логические операции. Кванторы”, “Логические выражения”).

Первым языком логического программирования был язык Planner, он был разработан Карлом Хьюитом в Лаборатории искусственного интеллекта Массачусетсского технологического института в 1969 г. В этом языке была заложена возможность автоматического вывода (получения) результата из данных и заданных правил путем перебора вариантов (совокупность которых называлась планом). Но самым известным языком логического программирования является ПРОЛОГ (Prolog), который был создан во Франции в Марсельском университете в 1971 г. Аленом Кольмеро (Colmerauer).

Ален Кольмеро
(Alain Colmerauer)

Программа на языке ПРОЛОГ содержит две составные части: факты и правила. Факты представляют собой данные, с которыми оперирует программа, а совокупность фактов составляет базу данных ПРОЛОГа, которая, по сути, является реляционной базой данных. Основная операция, выполняемая над данными, — это операция сопоставления, называемая также операцией унификации или согласования. Правила состоят из заголовка и подцелей. Выполнение программы, написанной на ПРОЛОГе, начинается с запроса и состоит в доказательстве истинности некоторого логического утверждения в рамках заданной совокупности фактов и правил. Алгоритм этого доказательства (алгоритм логического вывода) и определяет принципы исполнения программы, написанной на ПРОЛОГе.

В отличие от программ, составленных на языках процедурного типа, предписывающих последовательность шагов, которые должен выполнять компьютер для решения задачи, на ПРОЛОГе программист описывает факты, правила, отношения между ними, а также запросы по проблеме. Например, пусть у нас есть следующие факты относительно того, кто является чьей мамой:

мама("Даша","Маша").

мама("Наташа","Даша").

Кроме этого, имеется правило, вводящее отношение бабушка:

бабушка(X,Y):-

мама(X,Z),

мама(Z,Y).

Теперь мы можем делать запросы на предмет того, кто бабушка того или иного человека, или кто является внучкой (внуком) определенной женщины:

бабушка("Наташа",X).

Ответ на этот запрос система ПРОЛОГ выдаст так:

X=Маша

Возможности применения языка ПРОЛОГ весьма обширны. Среди наиболее известных — применение в символической математике, планировании, автоматизированном проектировании, построении компиляторов, базах данных, обработке текстов на естественных языках. Но, наверное, самое характерное применение ПРОЛОГа — это экспертные системы.

На сегодняшний день существует целый класс логических языков; так, от языка Planner также произошли логические языки программирования QA-4, Popler, Conniver и QLISP. Языки программирования Mercury, Visual Prolog, Oz и Fril произошли уже от языка Prolog.

Первым языком функционального типа является язык ЛИСП, созданный в Массачусетсском технологическом институте в 1956–1959 гг. Джоном Маккарти, который в 1956 г. на Дармутской конференции (США) впервые предложил термин “искусственный интеллект”.

Джон Маккарти (John McCarthy)

И хотя до сих пор не утихают споры вокруг этого термина и развившегося научного направления в его рамках, исследователи единодушны в использовании функциональных и логических языков для данной области. Значительное число работ по искусственному интеллекту реализовано на ЛИСПе.

После своего появления ЛИСПу присваивали много эпитетов, отражающих его черты: язык функций, символьный язык, язык обработки списков, рекурсивный язык. С позиций сегодняшней классификации ЛИСП определяется как язык программирования функционального типа, в основу которого положен метод -исчисления (метод -исчисления разработан в 30-е годы прошлого столетия А.Черчем в качестве строгой математической модели для вычислимых функций, см. “Теория алгоритмов”).

Программа, написанная на функциональном языке, состоит из неупорядоченного набора уравнений, определяющих функции и значения, которые задаются как функции от других значений. Программы и данные ЛИСПа существуют в форме символьных выражений, которые хранятся в виде списковых структур. ЛИСП имеет дело с двумя видами объектов: атомами и списками. Атомы — это символы, используемые для идентификации объектов, которые могут быть числовыми и символьными (понятия, материалы, люди и т.д.). Список — это последовательность из нуля или более элементов, заключенных в круглые скобки, каждый из которых является либо атомом, либо списком. Над списками выполняются три примитивные операции: извлечение первого элемента списка; получение оставшейся части списка после удаления первого элемента; объединение первого элемента списка L и оставшейся части списка Q.

Тексты программ на функциональных языках программирования только описывают способ решения задачи, но не предписывают последовательность действий для решения.

В качестве основных свойств функциональных языков программирования обычно рассматриваются следующие: краткость и простота; строгая типизация; модульность; функции — объекты вычисления; чистота (отсутствие побочных эффектов); отложенные (ленивые) вычисления.

Кроме ЛИСПа, к функциональным языкам относят РЕФАЛ (разработан в середине 60-х годов В.Ф. Турчиным в МГУ им. М.В. Ломоносова), Haskell, Clean, ML, OCaml, F#.

Приведем пример описания известного алгоритма быстрой сортировки списка на языке Haskell:

qsort [] = []

qsort (x:xs) = qsort elts_lt_x ++ [x]

++ qsort elts_greq_x where

elts_lt_x = [y | y <- xs, y < x]

elts_greq_x = [y | y <- xs, y >= x]

Здесь записано, что пустой список уже отсортирован. А сортировка непустого списка состоит в том, чтобы разбить список на три: список элементов, меньших головы исходного списка, голова исходного списка ([x]) и список элементов хвоста исходного списка, больше или равных x.

Объектно-ориентированные языки

Объектно-ориентированные языки — это языки, в которых понятия процедуры и данных, используемых в обычных системах программирования, заменены понятием “объект” (см. статью “Объектно-ориентированное программирование”). Языком объектно-ориентированного программирования в чистом виде считается SmallTalk, возможности объектно-ориентированного программирования заложены также в Java, C++, Delphi.

Дальнейшее развитие современного программирования связано с так называемым “параллельным программированием”. Для реализации этой технологии разрабатываются специализированные объектно-ориентированные языки. К языкам такого типа относят, например, MC# (mcsharp) — высокоуровневый объектно-ориентированный язык программирования для платформы .NET, поддерживающий создание программ, работающих в распределенной среде с асинхронными вызовами.

Структура языка программирования

Между существующими языками программирования есть принципиальные расхождения в концепции построения языков, особенно это справедливо для более ранних языков, но все эти языки потому и называются языками программирования, что они с точки зрения внутренней системы построения имеют одинаковое формальное строение.

Любой язык программирования состоит из предложений (операторов). Предложения (как и слова) определены над неким алфавитом С. Синтаксис языка описывает множество предложений над алфавитом С, которые внешне представляют правильно сформированные программы.

Синтаксис языка — это правила получения слов и предложений этого языка. Синтаксис схематически описывается с помощью определенных грамматических правил.

Знание формального языка (алфавита + синтаксиса) хотя и достаточно для установления синтаксической корректности программы, однако недостаточно для понимания ее назначения и способа действий. Значение и способ действия программы на языке программирования уточняются путем задания семантики.

Семантика языка — это правила интерпретации слов формального языка, т.е. установления значения отдельных языковых элементов.

Для определения формальных языков, в том числе для языков программирования, используют БНФ (формы Бэкуса — Наура) и синтаксические диаграммы. Это два взаимозаменяемых способа описания.

При описании языка программирования через БНФ используются следующие обозначения:

1) <..>— определяемое слово;

2) R — правило из синтаксиса для формирования слова;

3) <e>::= — БНФ-правило.

Каждое R состоит из терминальных слов или лексем языка и, возможно, следующих символов:

· | — или;

· [..] — данный элемент присутствует в БНФ;

· {..} — данное вхождение может быть использовано в БНФ;

· {..}* — данное вхождение может быть использовано в БНФ конечное число раз.

Пример 1. Приведем пример БНФ-правила, определяющего целое число.

Читается это правило так: “Целое число — это символ 0 или последовательность символов, которая может начинаться символом “–”, а далее следует отличная от нуля цифра, вслед за которой может следовать любая конечная последовательность цифр”.

Специальную, схожую с БНФ, форму описания формальных языков представляют синтаксические диаграммы. В синтаксических диаграммах используются три типа элементов: овал/круг, прямоугольник, стрелки. В овалах помещаются терминальные слова или лексемы, в прямоугольниках — определяемые слова. Графическое представление языка через синтаксические диаграммы делает описание языка наглядным.

Пример 2. Описание целого числа с помощью синтаксической диаграммы.

Методические рекомендации

Согласно Примерной программе, необходимо, чтобы школьники представляли современную классификацию языков программирования, а также ориентировались в областях применения каждого из них. Проще всего изложение данной темы проводить после того, как уже произошло подробное знакомство с одним из языков программирования.

Следует рассказать, почему возникают новые языки и совершенствуются старые: в первую очередь это происходит при поиске средства для быстрого написания сложных программ, которые к тому же не содержали ошибок. Известен пример, когда создание языка АДА (назван так в честь первой женщины-программиста Ады Лавлейс, дочери Байрона) было инициировано в 1974 году в Министерстве обороны США. Американские военные осознали, что они теряют много времени, усилий и денег на разработку и сопровождение встроенных компьютерных систем (например, систем наведения ракет), а трудноуловимые ошибки языков программирования приводят к настоящим катастрофам.

Декларативные языки были очень популярны в конце 80-х — начале 90-х годов прошлого столетия, они были названы языками программирования искусственного интеллекта для компьютеров пятого поколения. Однако надежды на их широкое распространение пока не оправдались. Возможно, потому, что существующие системы функционального и логического программирования не позволяют создавать быстро работающие программы для содержательных задач. Не исключено, что их время просто еще не наступило.

Выбирая стратегию преподавания темы “Алгоритмизация и программирование”, необходимо учитывать, что задача общеобразовательного курса — это в большой степени выработка определенного стиля мышления, формирование наиболее общих навыков, умений и представлений, нежели освоение тех или иных конкретных языков и технических средств программирования. В то же время, такой курс должен служить базой для последующего профессионального изучения программирования в высшей школе или старших классах средней школы (в рамках профессионального обучения).

В настоящее время существуют два наиболее распространенных подхода к преподаванию программирования:

1) преподавание на основе специально разработанного языка учебного языка, ориентированного на обучение основным навыкам программирования;

2) изучение одного или нескольких языков программирования, широко используемых на практике при решении научных и хозяйственных задач (такие языки можно назвать стандартными).

Первый подход часто используется при преподавании основ программирования в младших классах средней школы с использованием специальных языков, например, Рапиры, Е-языка, LOGO. Эти языки учитывают возможности школьников младших классов. Такой подход хорош при углубленном изучении информатики в 5–6-х классах.

Относительно второго подхода можно сказать, что большинство современных реализаций стандартных языков загружено большим количеством технических деталей и сложны в изучении. Тем не менее наиболее приемлемым для общеобразовательной школы, где курс информатики преподается в 8–11-х классах, является обучение теоретическим основам программирования на базе стандартного языка. При этом не обязательно вдаваться в глубины языка. Учащиеся, которых он заинтересует, могут сделать это и сами. Наибольшее внимание следует уделить переходу от алгоритмических структур к их программной реализации на языке программирования.

Здесь стоит отметить, что Pascal первоначально создавался как учебный язык, но со временем получил широкое распространение в качестве стандартного языка и развитие в виде объектно-ориентированного языка с визуальной технологией программирования Delphi. За основу курса в 8–9-х классах можно взять Pascal или Basic, а в качестве расширенного (факультативного) курса в 10–11-х классах ознакомить учащихся с их объектно-ориентированными расширениями (Delphi и Visual Basic). У каждого языка есть свои сторонники и противники, и конечный выбор остается за учителем.

Существует два основных подхода к изучению языка программирования: формальный и “программирование по образцу”. Первый основан на формальном (строгом) описании конструкций языка программирования (синтаксиса языка и его семантики) тем или иным способом (с помощью синтаксических диаграмм, мета-языка или формального словесного описания, в частности, семантики) и использовании при решении задач только изученных, а следовательно понятных, элементов языка. При втором подходе школьникам сначала выдаются готовые программы, рассказывается, что именно они делают, и предлагается написать похожую программу или изменить имеющуюся, не объясняя до конца ряд “технических” или несущественных, с точки зрения учителя, для решения задачи деталей. При этом говорится, что точный смысл соответствующих конструкций вы узнаете позднее, а пока поступайте аналогичным образом. Второй подход дает возможность так называемого “быстрого старта”, но создает опасность получить полуграмотных пользователей среды программирования, т.е. людей, которые используют в своей практике достаточно сложные конструкции, но не могут четко объяснить, почему в том или ином случае нужно применять именно их, и как они работают. В результате рано или поздно такие “программисты” сталкиваются с ошибками, исправить которые они просто не в состоянии — им не хватает знаний.

Одна из задач школьной информатики — научить именно формальному подходу, в частности, при применении различных определений. И формальное изучение языка программирования этому немало способствует. Но и без хороших примеров (образцов) при обучении программированию школьников не обойтись. И чем младше ученики, тем больше примеров необходимо приводить при описании языка (иногда даже заменяя ими строгое определение). Другое дело, что следует добиваться того, чтобы в результате обсуждения примера все его детали оказались понятны школьникам (обязательно нужно объяснить, как и почему это работает, в том числе опираясь на уже изученный формальный материал). В этом случае сильные ученики получат возможность понять все досконально и смогут использовать полученные знания в дальнейшем, а остальные приобретут конкретные навыки и оставят для себя возможность вернуться при необходимости к формальным определениям позже.

* В статье использованы материалы энциклопедии “Информатика” под ред. Д.А. Поспелова и книги Е.В. Андреевой, Л.Л. Босовой, И.Н. Фалиной “Математические основы информатики”, а также материалы, подготовленные Г.И. Сыркиным.

** Автором данного пункта является Г.И. Сыркин.

Продолжение