Курсы повышения квалификации
Математические основы информатики
А.Г. Гейн
Учебный план
| №_ГАЗЕТЫ |
Лекция |
17/2007 |
Лекция 1. Что такое
“математические основы информатики”. Почему
информатику нередко считают близкой род-
ственницей математики? Верно ли это? Возможна ли
информатика без математики? Какая математика
нужна для освоения
информатики? Может ли школьная математика дать
основу для информатики?
Информация и ее кодирование.
Математика кодов. Коды, исправляющие ошибки.
Экономное кодирование. |
18/2007 |
Лекция 2. Математические модели
формальных исполнителей. Что такое формальная
обработка информации? Конеч-
ные автоматы. Что первично: язык или исполнитель?
Грамматика языка. Распознаваемые языки.
Универсальные исполни-
тели (машина Тьюринга, машина Поста). |
19/2007 |
Лекция 3. Алгоритм и его свойства.
Алгоритмическая неразрешимость. Вычислимость.
Сложность. |
| Контрольная работа № 1. |
20/2007 |
Лекция 4. Графы. Графы и орграфы. В каких
задачах они возникают? Различные свойства графов
(эйлеровость, гамильто-
новость, планарность, двудольность). Сети. Потоки
в сетях. Представление графов. Основные
алгоритмы на графах. |
21/2007 |
Лекция 5. Логические модели в информатике.
Алгебра высказываний. Булевы функции.
Нормальные формы. Полные
классы булевых функций. Релейно-контактные
схемы. Вентили. Математические модели процессора
и памяти компьютера. Предикаты и отношения.
Реляционная алгебра. Теоретические основы
реляционных СУБД. Языки логического
программирования и их математическое основание. |
| Контрольная работа № 2. |
22/2007 |
Лекция 6. Компьютерная теория чисел и
вычислительная геометрия. Зачем нужна теория
чисел в компьютерных
науках? Гонка за простыми числами. Как разложить
число на множители? Чем отличается теоретическая
геометрия от
вычислительной? Почему гладко на бумаге, но
коряво на компьютере? Основные правила и
алгоритмы вычислительной
геометрии. |
| 23/2007 |
Лекция 7. Защита информации. Защита
символьной информации. Что нужно защищать?
Электронная подпись. Системы
верификации. Криптосистемы с открытым ключом.
Защита графической информации. Математика
электронных водяных знаков. |
| 24/2007 |
Лекция 8. Основы методики преподавания
математических основ информатики. |
| Итоговая работа |
Лекция 2.
Математические модели формальных исполнителей
“Изяществу зябко в этом суетном
свете”. Такую фразу сочинил компьютер по одной
из первых программ генерации текстов на
естественных языках. Но эмоция, переданная этой
фразой, конечно, недоступна компьютеру. И смысл
этой фразы компьютер понять не может. Потому что
он — всего лишь формальный исполнитель.
В нашем общественном сознании слово
“формальный” имеет, как правило, негативный
оттенок. Презрительным клеймом “формалист” мы
награждаем чиновника, который действует
исключительно на основании данных ему
предписаний, не желая вникать в суть
поставленной перед ним проблемы.
Но всегда ли плохо быть формальным
исполнителем? Будет ли рад хозяин овчарки, когда
по команде “Фас!” его четвероногий друг
задумается, стоит ли связываться с бандитом. Или
когда самолет в ответ на движение пилотом
штурвала продолжит лететь прежним курсом, потому
что разворот делать не хочется. А оператор
ядерного реактора, забросив инструкцию, будет
управлять им по наитию. Согласитесь, что даже
человеку временами быть формальным исполнителем
просто необходимо. Что касается устройств для
автоматической обработки информации, для них
неформальный путь просто невозможен. Напомним,
что, как отмечалось в лекции 1, информатика
занимается изучением как раз процессов
автоматизированной обработки информации.
Обработка (преобразование) информации
— достаточно широко понимаемый информационный
процесс. Под обработкой информации понимают
получение новой информации из уже имеющейся или
преобразование формы представления информации.
Детектив собрал улики и указал, кто
совершил преступление. Математик сопоставил
известные ему утверждения и доказал новую
теорему. Д.И. Менделеев на основе информации о
химических свойствах элементов сформулировал
периодический закон. Во всех этих примерах в
результате обработки информации появилась новая
информация.
Обработкой информации следует
признать и вычисление суммы двух чисел — ведь из
двух известных данных получается новое, до того
неизвестное. Обработкой информации является и,
например, перевод предложения с русского языка
на иностранный.
На первый взгляд между процессами
обработки информации, указанными в двух
предыдущих абзацах, большая разница. Главное
отличие здесь в том, что для розыска преступника
или доказательства новой теоремы нет и не может
быть указано жестких правил, как должна
обрабатываться исходная информация. Как говорят,
человек в этих случаях действует эвристически.
Складывая два числа, мы уже руководствуемся
жестко указанными правилами. Такую работу можно
поручить техническому устройству, которое
способно понимать и исполнять предписанную ему
инструкцию. Устройства, управляемые с помощью
инструкций и выполняющие свою работу
автоматически, называют программируемыми и
говорят, что свою работу они исполняют формально.
В частности, можно говорить и о формальной
обработке информации. Исполнитель, производящий
такую обработку, не должен вникать в смысл
выполняемых им действий; поэтому формальная
обработка информации, как правило, касается
изменения формы ее представления, а не
содержания.
Итак, под обработкой информации удобно
понимать любое преобразование ее содержания или
формы представления.
Однако каким бы ни был способ
обработки информации — формальным или
эвристическим, существует нечто или некто,
выполняющий эту обработку. Его обычно называют исполнителем.
Формальные исполнители могут быть
устроены весьма по-разному. Чтобы их изучать, как
и в любой науке, используется моделирование.
Какие математические модели применяют для
исследования формальных исполнителей, мы и
расскажем в этой лекции.
§ 3. Формальный исполнитель: автомат
Человек весьма преуспел в создании
разнообразных устройств, выполняющих ту или иную
работу в соответствии с четкой инструкцией. При
этом он уже не обязан постоянно находиться около
этого устройства, чтобы управлять им. В этом
случае говорят, что устройство выполняет работу
автоматически, а само такое устройство называют автоматом.
В реальности автоматы бывают весьма
разными. Это может быть автомат по продаже
билетов на поезда пригородного сообщения, или
автомат по расфасовке готовой продукции, или
автомат по изготовлению каких-либо деталей.
Автоматы последнего вида нередко называют промышленными
роботами.
С точки зрения информатики совершенно
все равно, из чего сделан автомат. Важно лишь то,
что он воспринимает некоторые сигналы как
команды и по каждой команде выполняет некоторое
действие, переходя из одного состояния в другое.
Поэтому можно считать, что каждый автомат
описывается набором возможных состояний,
списком допустимых команд и перечислением того,
из какого состояния в какое переходит автомат
под воздействием каждой команды. Например, если
команд только две, то их можно обозначить
буквами, скажем, a и b, или цифрами,
состояния автомата — буквами q1, q2, ..., qm,
а перечислить варианты перехода из одного
состояния в другое можно с помощью таблицы (см.
табл. 1).
Таблица 1
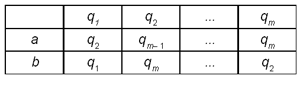
В клетке, стоящей на пересечении
строки и столбца, указывается то состояние, в
которое переходит автомат, находившийся в
состоянии, которое указано в заголовке того же
столбца, и получивший команду, указанную в
заголовке той же строки. Каждому ясно, что такая
таблица представляет собой информационную
модель реального автомата.
Автомат можно описать и другой
информационной моделью — орграфом*. Вершинами
орграфа являются состояния автомата, дугами —
переходы из одного состояния в другое. На каждой
дуге имеется отметка, показывающая, по какой
команде осуществляется переход. Тогда автомат,
описанный табл. 2, изобразится так, как показано
на рис. 1.
Таблица 2
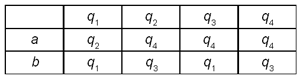
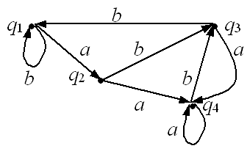
Рис. 1
Одно из состояний называется
начальным — именно в нем находится автомат до
начала работы. Договоримся начальное состояние
всегда обозначать q1. Некоторые из состояний
являются заключительными — приведение автомата
в это состояние является целью управления
автоматом с помощью той или иной
последовательности команд. Например, если это
автомат по продаже железнодорожных билетов, то в
начальном состоянии автомат ожидает, что в
монетоприемник начнут поступать монеты.
Конечных состояний два: выдача билета и возврат
денег. Кроме того, имеются промежуточные
состояния — подсчет суммы денег, переданных в
автомат к этому моменту. Команды, переводящие
автомат из одного состояния в другое, — это
опускание монеты в монетоприемник, нажатие
кнопки выдачи билета или нажатие кнопки возврата
денег. Обозначать тот факт, что данное состояние
конечное, будем буквой К в скобках около
обозначения данного состояния. Например, q2(К).
Ясно, что целью управления автоматом
является выдача ему такой последовательности
команд, которая переводит его из начального
состояния в какое-либо конечное. Поскольку
каждая команда обозначена буквой, то набор
команд, понимаемых данным автоматом, можно
считать некоторым алфавитом А. Тогда
последовательность команд, т.е. программа, будет
записываться как слово в этом алфавите. Например,
слово abа переводит автомат, описанный табл. 2,
из начального состояния q1 в состояние q4.
Можно сказать, что слово abа задает на орграфе
данного автомата некоторый маршрут из состояния q1
в состояние q4.
Множество всех тех слов, которые
переводят автомат из начального состояния в одно
из конечных состояний, образует некий формальный
язык. Этот язык называется языком,
распознаваемым данным автоматом. Если для
некоторого языка существует хотя бы один
автомат, который этот язык распознает, то такой
язык называют распознаваемым.
На рис. 2 изображен автомат, имеющий
два состояния — q1(К) и q2 — и
понимающий две команды, которые обозначены
цифрами 0 и 1. Легко сообразить, что
распознаваемый этим автоматом язык состоит из
тех и только тех слов, которые содержат четное
количество единиц и любое количество нулей.
Иными словами, этот автомат подсчитывает сумму
цифр в числе, записанном в двоичной системе
счисления.
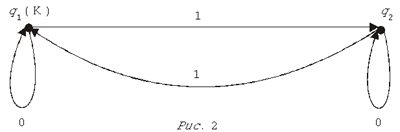
Рис. 2
Пусть теперь у нас имеется
фиксированный алфавит А, и L — некоторое
множество слов, составленное из символов данного
алфавита. Всегда ли можно построить такой
автомат, чтобы множество L было для него
распознаваемым языком? Ответ отрицателен.
Теорема. Пусть А = {a, b}, L =
{anbn, где n пробегает множество
всех натуральных чисел}. Множество L не
является распознаваемым языком.
Запись an, фигурирующая в
формулировке этой теоремы, означает, что буква а
повторена n раз.
Доказательство теоремы использует
один из важнейших математических методов — от
противного. Итак, предположим, что L —
распознаваемый язык. Значит, существует такой
автомат, который любым словом этого языка
переводится в некоторое конечное состояние.
Пусть этот автомат имеет k состояний.
Рассмотрим слово ak bk . Оно
принадлежит языку L и, следовательно,
переводит этот автомат из начального состояния q1
в некоторое конечное состояние qs.
Поскольку буква а повторяется не меньшее
число раз, чем количество состояний автомата,
найдется такое состояние qt, которое за
первые k применений буквы а будет
пройдено дважды (см. рис. 3). Пусть первый раз
автомат перейдет в состояние qt в
результате применения au, а следующий
раз окажется в том же состоянии после применения au
+ v. Рассмотрим слово ak + v bk .
Ясно, что применение этого слова к начальному
состоянию q1 переведет его в то же самое
конечное состояние qs. Это означает, что
данное слово также распознаваемо данным
автоматом и, значит, должно принадлежать языку L.
Но в множестве L такого слова нет. Полученное
противоречие показывает, что сделанное
допущение неверно, т.е. автомата, для которого
данное множество служило бы распознаваемым
языком, не существует.

Рис. 3. Маршрут на орграфе
автомата от начального состояния q1 до
конечного состояния qs (до состояния qt
буква а на дугах стоит u раз, на цикле —
еще v раз)
Раз не всякое множество слов
представляет собой распознаваемый язык,
возникает вопрос, какие множества годятся для
этого. Математики нашли удобные способы описания
распознаваемых языков, и эти способы легли в
основу конструирования всех ныне существующих
языков программирования.
Вопросы и задания
1. Какими двумя информационными
моделями может быть представлен автомат?
2. Что такое язык, распознаваемый
данным автоматом?
3. Какой язык называется
распознаваемым?
4. Для автомата, изображенного на рис.
1, определите, в каком состоянии он будет
находиться после исполнения последовательности
команд
а) abba; в) babaabaaa;
б) ababbabbb; г)* anbn.
5. Для автомата, изображенного на рис.
2, составьте описание в форме таблицы.
6. Постройте в виде графа
информационную модель автомата, заданного табл.
3.
Таблица 3
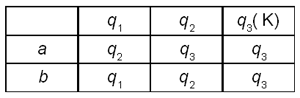
7. Какой язык над двухсимвольным
алфавитом {0, 1} распознается автоматом,
изображенным на рис. 4?
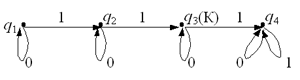
Рис. 4
8. Какой язык над двухсимвольным
алфавитом {a, b} распознается автоматом,
заданным табл. 3?
9. Изобразите в виде графа
информационную модель автомата, который бы
распознавал язык над алфавитом {0, 1}, состоящий из
всех слов, содержащих ровно 5 подряд идущих
единиц.
10. Изобразите в виде графа
информационную модель автомата, который бы
распознавал язык над алфавитом {0, 1}, состоящий из
всех слов, содержащих ровно 5 единиц.
11. Изобразите в виде графа
информационную модель автомата, который бы
распознавал язык над алфавитом {0, 1}, состоящий из
всех слов, начинающихся с единицы (т.е. этот
автомат отличает натуральные числа, записанные в
двоичной системе счисления, от произвольных
последовательностей символов 0 и 1).
12. Среди перечисленных ниже языков L1,
L2, L3, L4, определенных
над двухсимвольным алфавитом {1; 2}, укажите
распознаваемые. Для каждого из распознаваемых
языков постройте распознающий его автомат, для
каждого из нераспознаваемых языков докажите, что
он нераспознаваем.
а) L1 состоит из всех слов,
которые представляют собой четные натуральные
числа, начинающиеся с цифры 1;
б) L2 состоит из всех слов,
количество единиц в которых — это натуральное
число, оканчивающееся цифрой 3;
в) L3 состоит из всех слов, в
которых количество двоек является простым
числом;
г) L4 состоит из всех слов,
которые представляют собой натуральные числа,
делящиеся на 3.
13. В чем с точки зрения информатики
заключается разница “в жизни по законам” и “в
жизни по понятиям”?
§ 4. Универсальный исполнитель
Компьютерные игры... Наверно, каждый,
кто хоть однажды имел дело с компьютером, видел, а
возможно, и сам играл в какую-либо компьютерную
игру. На экране одни объекты в виде живых существ
или технических устройств подчиняются командам
играющего, другие — управляются компьютером,
который исполняет заданную программу. Все эти
объекты — формальные исполнители, каждый со
своим набором допустимых действий. Только
объекты эти не реальные, а имитируемые
компьютером. Получается, что с помощью одного
формального исполнителя имитируются другие.
Если попытаться сформулировать, что
значит один исполнитель имитируется с помощью
другого, то получится следующее. Говорят, что
формальный исполнитель А имитирует
формального исполнителя В, если
— каждому объекту, над которым
выполняет действия исполнитель В, однозначно
соответствует объект, над которым выполняет
действия исполнитель А (имитация среды
исполнителя);
— каждому допустимому действию
исполнителя В над тем или иным объектом среды
однозначно сопоставлено допустимое действие
исполнителя А над соответствующим объектом
его среды (имитация действий);
— каждая инструкция, составленная для
исполнителя В и приводящая при ее исполнении
к определенному результату (т.е. к определенному
состоянию среды исполнителя и него самого), может
быть преобразована имитацией допустимых
действий в инструкцию для исполнителя А,
исполнение которой приводит к соответствующему
результату в среде исполнителя А.
Впрочем, предположение, что у
исполнителей А и В разная среда, в которой
они существуют, не принципиально с
информационной точки зрения. Например,
исполнитель А имеет дело с числами, а В
преобразует графические изображения. Но вы уже
знаете, что фактически в каждом из этих случаев
речь идет о преобразовании подходящим образом
закодированной информации. Более того, можно
считать, что используется один и тот же двоичный
код. В этом смысле можно считать, что среда
исполнителя просто одинакова — информация,
представленная в форме закодированного
сообщения.
Один из важнейших вопросов
теоретической информатики звучит так:
существует ли такой формальный исполнитель, с
помощью которого можно имитировать любого
формального исполнителя? Такого исполнителя
естественно назвать универсальным. Легко
понять, что как физическое устройство
универсальный исполнитель не существует — ведь
информация может кодироваться как угодно
длинными сообщениями, а любой физический
носитель конечен. Если же вести речь об
универсальном исполнителе как идеальном
объекте, то оказывается, что ответ на заданный
вопрос положителен. И получен он был почти
одновременно и независимо двумя выдающимися
учеными — А.Тьюрингом (в 1936 г.) и Э.Постом (в 1937 г.).
Предложенные ими исполнители отличались друг от
друга, но оказалось, что они могут имитировать
друг друга, а главное — имитировать вообще
любого формального исполнителя.
Универсального исполнителя принято
называть машиной. Также принято давать машинам
имена их изобретателей. Так что универсального
исполнителя, придуманного А.Тьюрингом, называют
машиной Тьюринга; исполнителя, описанного
Э.Постом, — машиной Поста. Позже появились и
другие универсальные исполнители, например,
машина Минского.
Итак, можно считать, что у нас имеется
сообщение, записанное в некотором алфавите, и его
требуется преобразовать в другое сообщение.
Конечно, написать инструкцию формальному
исполнителю для обработки конкретной пары
сообщений — дело нехитрое. Но вы уже знаете, что
реальный интерес представляют инструкции (т.е.
алгоритмы), позволяющие решать целый класс
однотипных задач, — так называемое “свойство
массовости алгоритма”. Например, такая задача: к
любому сообщению приписать справа еще один
заранее заданный символ. Если, скажем,
последовательность одинаковых символов
выступает кодом натурального числа — количество
символов в последовательности и есть кодируемое
натуральное число, — то фактически речь идет о
создании алгоритма увеличения числа на 1.
Естественно считать, что сообщение
записано на ленту. Более того, удобно
представлять себе эту ленту разделенной на
одинаковые клетки, и в каждой клетке записан
ровно один символ сообщения. Поскольку сообщения
могут быть как угодно длинными, то ленту
договоримся представлять себе бесконечной.
Пустые клетки будем считать заполненными
символом “пробел”. Тем самым, мы объявили, что
любой алфавит, который будет использоваться нами
для записи сообщений на этой ленте, обязательно
содержит “пробел”. Договоримся обозначать его а0.
Остальные символы алфавита, используемого для
записи сообщений на ленту, будем обозначать а1,
а2, ..., аn. Если, к примеру, нам
требуется записать задачу вычисления суммы двух
чисел, то алфавит можно взять таким: а0;
1; 2; 3; 4; 5; 6; 7; 8; 9; 0; ,; +; =. Для конкретной пары данных
(т.е. двух чисел) запись на ленте может выглядеть,
например, так, как показано на рис. 5.
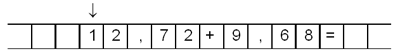
Рис. 5
Мы, конечно, не будем на ленте в пустых
клетках писать символ а0, подразумевая его
там. Кроме того, договоримся, что первый символ
сообщения, отличный от пробела, всегда стоит в
одной и той же клетке — на рис. 4 она отмечена
Ї. Эту клетку будем называть начальной.
Сообщение, записанное на ленте,
обрабатывается неким устройством, и результат
снова записывается на ленту. Поскольку
исполнитель формальный, он не вникает в смысл
сообщения, а по составленной для него инструкции
заменяет одни символы на другие. Нас не
интересует, как физически осуществляется такая
замена, поэтому можно представить, что вдоль
ленты движется некий автомат, который считывает
символ из клетки на ленте, обрабатывает
полученную информацию, печатает в клетке другой
символ (если это предписано инструкцией) и
сдвигается к соседней клетке — вправо или влево.
Вы уже знаете, что каждый автомат
описывается набором состояний. Принято
обозначать состояния указанного
считывающе-печатающего автомата буквами q0,
q1, q2, ..., qm. При этом
договоримся, что при включении автомата, т.е. в
начале работы, он всегда находится в одном и том
же состоянии, которое мы будем обозначать q0,
и располагается напротив начальной клетки.
Таким образом, машина Тьюринга
формально описывается набором двух алфавитов: А
= {а1, а2, ..., а} и Q = {q0,
q1, q2, ..., qm}. Алфавит А
называется внешним и служит для записи
исходных сообщений, алфавит Q называется внутренним
и описывает набор состояний
считывающе-печатающего устройства. Изображать
машину Тьюринга будем так, как показано на рис.
6.
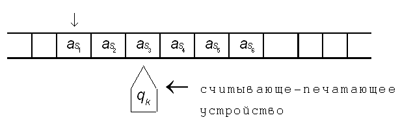
Рис. 6
На рис. 6 показан момент работы
машины Тьюринга, когда считывающе-печатающее
устройство обозревает третью клетку от
начальной (в ней к этому моменту оказался символ аs3)
и находится в состоянии qk.
Итак, допустимые действия машины
Тьюринга таковы:
— записать какой-либо символ внешнего
алфавита в секцию ленты (символ, бывший там до
того, затирается);
— сместиться в соседнюю секцию;
— сменить состояние на одно из
обозначенных символом внутреннего алфавита;
— прекратить работу (остановиться).
Конечно, в этом перечислении в каждой
строке указано не одно действие, а группа
действий одного вида — действий “записать
символ внешнего алфавита” столько, сколько этих
символов, сместиться в соседнюю секцию можно
вправо, а можно влево, действий по изменению
состояния столько, сколько этих состояний (т.е.
сколько символов внутреннего алфавита).
Теперь надо сказать, как записываются
команды на выполнение указанных действий. Каждая
команда машины содержит не более одного действия
из каждой группы действий и имеет вид
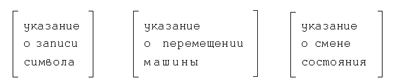
Фактически команды выглядят так:
ai 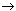 qj — в обозреваемую секцию
записать ai, сместиться вправо (к
следующей секции) и перейти в состояние qj; qj — в обозреваемую секцию
записать ai, сместиться вправо (к
следующей секции) и перейти в состояние qj;
ai 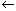 qj — в обозреваемую секцию записать ai,
сместиться влево и перейти в состояние qj;
qj — в обозреваемую секцию записать ai,
сместиться влево и перейти в состояние qj;
aiSqj — в
обозреваемую секцию записать ai, остановиться
и перейти в состояние qj.
Для осуществления действий машина
Тьюринга имеет операционно-логический блок. У
этого блока имеется два входа: через один из них
поступает информация о том, какой символ стоит в
обозреваемой ячейке, через другой — информация о
том, в каком состоянии находится машина на данном
шаге своей работы. Эта информация однозначно
определяет, какую именно команду следует
выполнить машине. Поскольку команда может
содержать указание на выполнение трех действий
— записи символа на ленту, смещения и смены
состояния — операционно-логический блок имеет
три выхода: запись символа A, смещение M и
смена состояния Q (см. рис. 7).
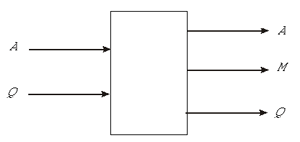
Рис. 7.
Операционно-логический блок машины Тьюринга
Поскольку у этого блока всего лишь два
входа, его реакцию на символы, подаваемые на них,
удобно представлять в виде прямоугольной
таблицы, в которой строки и столбцы помечены
символами внешнего и внутреннего алфавитов
соответственно (см. табл. 4). В клетки таблицы
записываются команды. Если машина находится
напротив клетки, где написано ai, а ее
состояние при этом есть qj, то
выполняется команда, стоящая на пересечении
строки, отмеченной символом ai, и столбца,
отмеченного символом qj.
Таблица 4
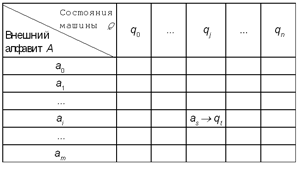
Эту таблицу называют функциональной
схемой данной машины; она-то и играет роль
инструкции (программы) для машины Тьюринга. Из
нее, в частности, видно, каковы внешний и
внутренний алфавиты машины.
Пусть, к примеру, на ленте записана
последовательность из некоторого количества
одного и того же символа “*”. Тогда
функциональная схема, приведенная в табл. 5,
заставляет машину Тьюринга увеличить на одну
количество звездочек в этой последовательности.
Таблица 5
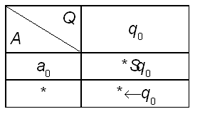
Доказать, что машина Тьюринга является
универсальным исполнителем, нельзя. Так же,
например, как нельзя доказать закон сохранения
энергии в физике. Но практика составления
алгоритмов показывает, что любую задачу, которую
сегодня умеет решать человек, можно
запрограммировать на машине Тьюринга. Этот
экспериментальный факт, называемый тезисом
Тьюринга, формулируют так: для задачи существует
алгоритм решения тогда и только тогда, когда
имеется подходящая машина Тьюринга, посредством
которой можно решить эту задачу.
Вопросы и задачи
1. Какого формального исполнителя
называют универсальным?
2. Что такое машина Тьюринга?
3. Чем одна машина Тьюринга отличается
от другой?
4. Что называют функциональной схемой
машины Тьюринга?
5. Верно ли, что машина Тьюринга с
написанной для нее функциональной схемой
является конечным автоматом?
6. Изобразите в виде
последовательности рисунков, как изменяется
информация на ленте при работе машины Тьюринга,
описанной функциональной схемой в табл. 5.
7. Следуя функциональной схеме,
описанной табл. 5, машина Тьюринга приписывает к
заданной последовательности звездочек еще одну
звездочку слева. Составьте функциональную схему,
согласно которой звездочка будет приписываться
справа от заданной последовательности.
8. Работа машины Тьюринга описана
следующей функциональной схемой:
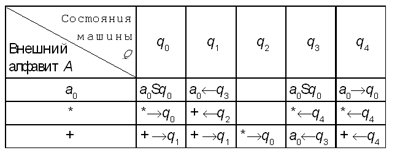
Определите, какое сообщение будет на
ленте после окончания работы машины, и укажите,
напротив какой ячейки в этот момент будет
находиться ее пишущий блок.
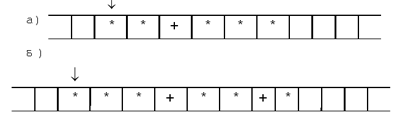
Рис. 8
в)

Рис. 9
9. На ленте машины Тьюринга записана
строка, состоящая из нескольких подряд идущих
символов “*”, за ними следует несколько символов
“#”, а в конце строки стоит символ “е” (один из
возможных вариантов такой строки приведен на рис.
5).
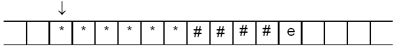
Рис. 10
Для каждой из приведенных ниже
функциональных схем определите, для решения
какой задачи она предназначена. (Совет: чтобы
получить убедительный ответ, примените
функциональную схему к разным вариантам
заполнения информационной ленты
последовательностями символов внешнего
алфавита.)
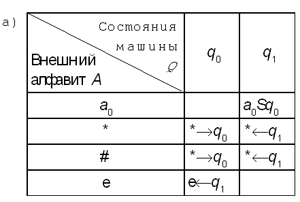
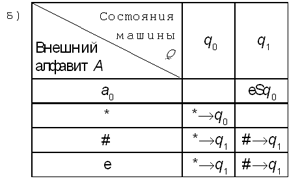
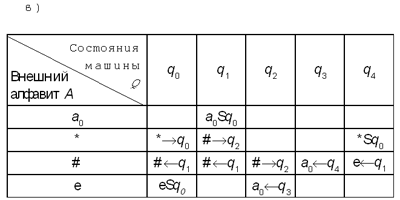
10. Пусть внешний алфавит состоит из
символа “a0” и цифр 0, 1, 2, ..., 9. На ленту
записывается натуральное число. Придумайте
машину Тьюринга и составьте для нее
функциональную схему, согласно которой данное
число будет увеличено на 1.
11. Пусть внешний алфавит состоит из
символа “a0” и цифр 0, 1, 2, ..., 9. На ленту
записано натуральное число. Составьте
функциональную схему для машины Тьюринга, с
помощью которой на ленте будет записана сумма
цифр этого числа. Ответ требуется записать
правее исходного числа, отделив от него пробелом.
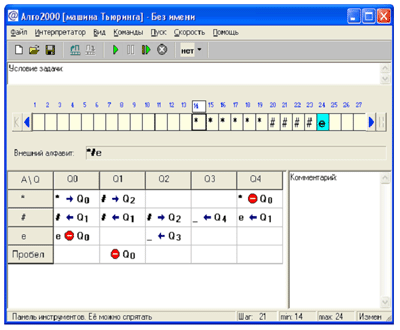
Рис. 11
P.S. Ощутить себя в роли машины Тьюринга
небесполезно, но утомительно. Мы рекомендуем
задания 8 и 9 проделать вручную. Что касается
заданий 10 и 11, то ручное тестирование
составленных вами функциональных схем может
оказаться неэффективным. В связи с этим мы
предлагаем воспользоваться компьютерной
реализацией машины Тьюринга, созданной
Р.Зартдиновым. Ее можно получить на сайте газеты
“Информатика” (inf.1sept.ru).
Вот как, к примеру, выглядит на этой машине
функциональная схема из задания 8 в) — отличия
состоят в том, что вместо буквы S изображен
дорожный знак, а вместо символа “a0”
пишется “_” (при занесении команды в клетку
таблицы нажимать, однако, надо клавишу “пробел”,
а не “_”). Программа снабжена подробной справкой
о том, как с ней работать. Интерфейс этой
программы очень прост. Кроме того, описание
данной реализации машины Тьюринга вы можете
найти в газете “Информатика” № 8, 2006. Там же вы
найдете разбор еще нескольких задач на
программирование машины Тьюринга; надо только
иметь в виду, что в них используется несколько
иная (что совершенно непринципиально) система
команд.
* Напомним, что граф — это совокупность точек,
называемых вершинами, и линий, соединяющих
некоторые из вершин. Если на линиях, соединяющих
вершины, указано направление, то граф называется ориентированным
(сокращенно орграфом), а линии называются его дугами.
В обычном графе, т.е. неориентированном, линии,
соединяющие вершины, называются ребрами.
Подробнее о графах речь пойдет в лекции 4. |