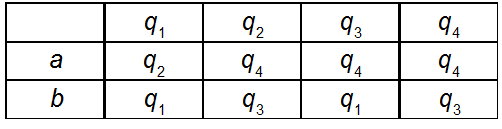
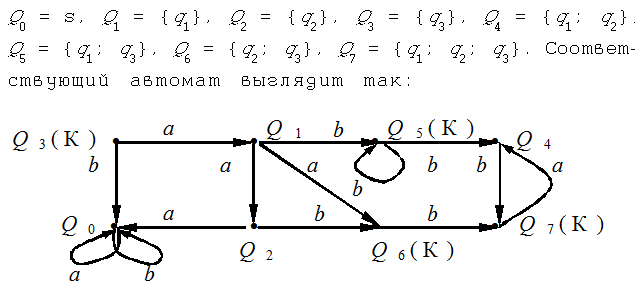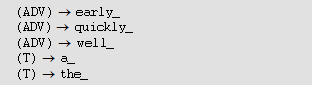СТРАНИЦЫ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

А.Г. Гейн,
г. Екатеринбург

Продолжение. Cм. № 1/2008

Автоматы и распознаваемые языки

В лекции 2 (напомним, что эти материалы дополняют лекции Педагогического университета “Первое сентября”, опубликованные в № 17–24/2007) рассматривалась математическая модель формального исполнителя — так называемый “конечный автомат”. Для читателя, оформившего подписку лишь с января 2008 г., мы в преамбуле этой статьи очень кратко повторим основные определения.

С точки зрения информатики совершенно все равно, из чего сделан автомат. Важно лишь то, что он воспринимает некоторые сигналы как команды и по каждой команде выполняет некоторое действие, переходя из одного состояния в другое. Поэтому можно считать, что каждый автомат описывается набором возможных состояний, списком допустимых команд и перечислением того, из какого состояния в какое переходит автомат под воздействием каждой команды. Например, если команд только две, то их можно обозначить буквами, скажем, a и b, или цифрами, состояния автомата — буквами q₁, q₂, ..., q_m, а перечислить варианты перехода из одного состояния в другое можно с помощью таблицы (см., например, табл. 1). В клетке, стоящей на пересечении строки и столбца, указывается то состояние, в которое переходит автомат, находившийся в состоянии, которое указано в заголовке того же столбца, и получивший команду, указанную в заголовке той же строки.

Автомат можно описать и другой информационной моделью — орграфом¹. Вершинами орграфа являются состояния автомата, дугами — переходы из одного состояния в другое. На каждой дуге имеется метка, показывающая, по какой команде осуществляется такой переход. Тогда автомат, описанный табл. 1, изобразится так, как показано на рис. 1. Обратите внимание, что из каждой вершины выходит столько стрелок, сколько символов в алфавите, при этом каждый символ употреблен ровно один раз.

Таблица 1

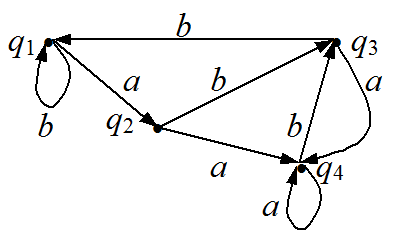
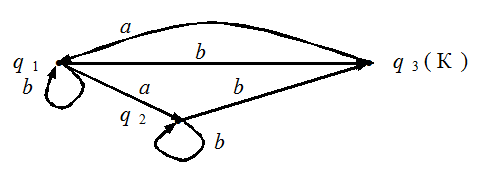
Рис. 1

Одно из состояний называется начальным — именно в нем находится автомат до начала работы. Договоримся начальное состояние всегда обозначать q₁. Некоторые из состояний являются заключительными — приведение автомата в это состояние является целью управления автоматом с помощью той или иной последовательности команд. Конечных состояний может быть несколько. Обозначать тот факт, что данное состояние конечное, будем буквой К в скобках около обозначения данного состояния. Например, q₂(К).

Ясно, что целью управления автоматом является выдача ему такой последовательности команд, которая переводит его из начального состояния в какое-либо конечное. Поскольку каждая команда обозначена буквой, то набор команд, понимаемых данным автоматом, можно считать некоторым алфавитом А. Тогда последовательность команд, т.е. программа, будет записываться как слово в этом алфавите. Например, слово abа переводит автомат, описанный табл. 2, из начального состояния q₁ в состояние q₄. Можно сказать, что слово abа задает на орграфе данного автомата некоторый маршрут из состояния q₁ в состояние q₄.

Множество всех тех слов, которые переводят автомат из начального состояния в одно из конечных состояний, образует некий формальный язык. Этот язык называется языком, распознаваемым данным автоматом. Если для некоторого языка существует хотя бы один автомат, который этот язык распознает, то такой язык называют распознаваемым.

В лекции 2 был приведен пример множества слов, которое не является распознаваемым языком. Поэтому возникают естественные вопросы: как можно узнать, распознаваем язык или нет; как строить распознаваемые языки; как построить автомат по распознаваемому языку. Именно эти вопросы мы и намерены обсудить в данной публикации.

§ 4. Недетерминированный автомат

Обратите внимание: в построенной выше модели автомата этот формальный исполнитель обязательно откликался на каждое к нему обращение с командой и реагировал на нее всегда однозначно. С точки зрения понятия “алгоритм” такое поведение формального исполнителя представляется совершенно естественным — оно отражает то свойство алгоритмов, которое называют детерминированностью (см. лекцию 3, § 5). Давайте, однако, предоставим автомату некоторую свободу. Пусть он уже не будет обязан однозначно реагировать на каждую команду, а может по той или иной команде переходить в какое-нибудь из состояний, или вообще не менять состояние. Конечно, мы по-прежнему можем изображать такой автомат размеченным орграфом, только теперь стрелок с одним и тем же символом алфавита, выходящих из одной вершины, может быть несколько или ни одной (см. рис. 2). Такой автомат называют недетерминированным. Как обычно, в нем одно состояние называют начальным; мы по-прежнему будем обозначать его q₁. Одно или несколько состояний являются конечными. Цель та же — перевести последовательностью команд автомат из начального состояния в какое-нибудь конечное. Как и ранее, языком, распознаваемым данным недетерминированным автоматом, называется множество слов, для каждого из которых существует хотя бы один путь, переводящий автомат из начального состояния в какое-либо конечное состояние. Отличие, однако, в том, что теперь слово (т.е. последовательность команд) вовсе не каждый раз переведет автомат из начального состояния в то же самое конечное.
А может и вообще перевести его в какое-нибудь промежуточное состояние. Например, слово bаb может перевести автомат, изображенный на рис. 2, из состояния q₁ как в состояние q₁, так и в состояние q₃. “Нам не дано предугадать, как наше слово отзовется” — едва ли поэт написал эти слова про недетерминированный автомат, но… Действительно, можно сказать, что недетерминированный автомат до определенной степени моделирует поведение человека — одни и те же слова могут приводить к разным реакциям, а иногда и просто к “зависанию”².

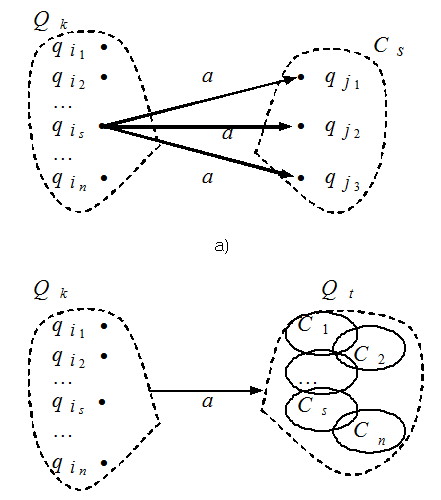
Рис. 2

Разумеется, всякий (обычный) автомат естественно рассматривать как частный случай недетерминированного автомата. Поэтому множество распознаваемых языков содержится в множестве всех языков, распознаваемых недетерминированными автоматами. Удивительно, что верно и обратное утверждение: всякий язык, распознаваемый каким-либо недетерминированным автоматом, является распознаваемым.

Для доказательства этого утверждения мы научимся по недетерминированному автомату строить обычный автомат, распознающий тот же самый язык. Вот как это делается.

Пусть {q₁, q₂, ..., q_m} — множество всех состояний недетерминированного автомата, причем q₁ — его начальное состояние. Построим множество В всех подмножеств этого множества. Элементы множества В будем обозначать большими буквами Q с индексами, при этом через Q₁ обозначим одноэлементное множество {q₁}. Как известно, В состоит из 2^m элементов. Именно их мы и возьмем в качестве состояний конструируемого автомата.

Определим теперь воздействия символов алфавита А на состояние Q_k. Пусть Q_k = {q_i1, q_i2, ..., q_in}. Для каждого символа а из А и q_is построим множество С_s по следующему правилу: рассмотрим все стрелки, выходящие в исходном автомате из состояния q_is и отмеченные символом а; тогда в С_s включаем все те состояния исходного автомата, которые записаны на концах этих стрелок (см. рис. 3a).

Рис. 3

А теперь объединим все множества С_s. Получившееся множество состояний совпадает с каким-то Q_t. В конструируемом автомате соединим состояния Q_k и Q_t стрелкой с меткой а на ней (см. рис. 3б). Могло, конечно, случиться так, что ни из одного элемента не выходит ни одной стрелки, помеченной а. Тогда из множества Q_k стрелка, отмеченная символом а, ведет в пустое множество.

Конечными для конструируемого автомата объявим те состояния, которые в качестве элемента содержат хотя бы одно конечное состояние недетерминированного автомата.

Построим, к примеру, такой автомат для недетерминированного автомата, изображенного на рис. 2. Множество В имеет восемь элементов:

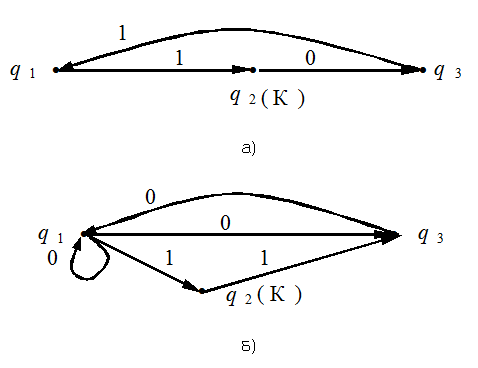
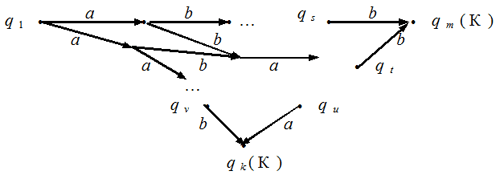
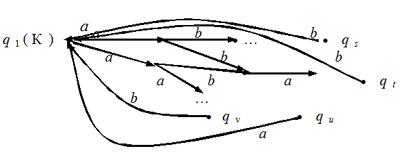
Рис. 4

Вернемся к доказательству утверждения. Пусть для некоторого слова имеется маршрут в орграфе недетерминированного автомата, который ведет из начального состояния q₁ в некоторое конечное, скажем, q_i. Но тогда тот же маршрут переводит построенный нами автомат из начального состояния Q₁ в то Q_l, которое содержит это самое q_i. Но такое Q_l отмечено как конечное состояние, так что выбранное нами слово принадлежит распознаваемому языку. И наоборот, если некоторое слово переводит автомат из начального состояния Q₁ в некоторое конечное состояние Q_l, то это Q_l содержит некоторое конечное состояние исходного недетерминированного автомата. Но тогда в орграфе недетерминированного автомата существует некоторый маршрут, размеченный символами данного слова и ведущий из начального состояния q₁ в то конечное, которое содержится в Q_l. Это означает, что множества распознаваемых слов у этих автоматов одинаковы.

Утверждение доказано.

О чем оно свидетельствует? А вот о чем: множество алгоритмов, управляющих обычными автоматами, и множество алгоритмов, управляющих недетерминированными автоматами, совпадают. Но для обычных автоматов эти алгоритмы обладают свойствами детерминированности и результативности, а для недетерминированных — нет. Это еще раз свидетельствует о том, что далеко не все так называемые “свойства алгоритмов” присущи всем алгоритмам (и потому не могут претендовать на роль “аксиом” в определении понятия “алгоритм”). Мы неформально говорили об этом в лекции 3. Далее мы обсудили это на вполне строгом и формализованном уровне.

Договоримся два автомата (неважно, будут ли они недетерминированными или обычными) называть эквивалентными, если распознаваемые ими языки совпадают. Естественно, к примеру, для заданного распознаваемого языка интересоваться минимальным автоматом среди всех автоматов, распознающих данный язык. Математики весьма преуспели в исследовании этого вопроса, однако рамки газетной статьи не позволяют сколько-нибудь подробно на этом остановиться.

Вопросы и задания

1. Для недетерминированного автомата, изображенного на рис. 2, определите те состояния, в которых может оказаться автомат после исполнения последовательности команд

а) abba;

б) ababbabbb;

в) babaabaaa;

г) aⁿbⁿ

(запись aⁿ означает, что буква а повторена n раз).

2. На рис. 5а и 5б изображены орграфы двух недетерминированных автоматов, распознающих слова над двухсимвольным алфавитом A = {0; 1}. Постройте для каждого из них эквивалентный конечный автомат.

Рис. 5

3. а) Определите, какой язык распознается недетерминированным автоматом, орграф которого изображен на рис. 5а.

б) Определите, какой язык распознается недетерминированным автоматом, орграф которого изображен на рис. 5б.

4. Можно ли построить недетерминированный автомат, эквивалентный автомату, орграф которого изображен на рис. 5б, но с меньшим числом состояний?

§ 5. Операции над языками

Отвлекаясь от смысла слов, хотя, разумеется, смысл — это главное, для чего слова употребляются³, можно сказать, что формально любой язык — это произвольное множество слов, составленных из символов некоторого фиксированного алфавита. Как и над любыми множествами, над языками можно выполнять теоретико-множественные операции — находить пересечение, объединение, дополнение.

Напомним, что пересечением двух множеств М₁ и М₂ называется такое множество М, которое содержит те и только те элементы, которые одновременно принадлежат обоим множествам М₁ и М₂. Пересечение множеств М₁ и М₂ обозначается как . Объединением множеств М₁ и М₂ называется такое множество М, которое содержит те элементы, которые принадлежат хотя бы одному из множеств М₁ и М₂. Объединение множеств М₁ и М₂ обозначается как . Наконец, дополнением к множеству М₁ называется множество М, которое содержит те и только те элементы, которые не принадлежат множеству М₁. Дополнение к множеству М₁ обозначается как .

Оказывается, что если эти операции применить к распознаваемым языкам, то в результате получится снова распознаваемый язык.

Теорема 1. Объединение и пересечение двух распознаваемых языков, а также дополнение к распознаваемому языку является распознаваемым языком.

Доказательство. Пусть L₁ и L₂ — распознаваемые языки, . Рассмотрим два недетерминированных автомата А₁ и А₂, первый из которых распознает язык L₁, а второй распознает язык L₂. Пусть они представлены соответствующими орграфами (см. рис. 6). Чтобы не путать состояния разных автоматов, во втором из них для обозначения состояний использована буква s; при этом через s₁ обозначено начальное состояние второго автомата.

Рис. 6

Чтобы построить автомат, распознающий , сделаем у автоматов А₁ и А₂ вершины q₁ и s₁ одной общей вершиной (см. рис. 7), все остальное оставим, как и было, в том числе конечными состояниями объявим те состояния, которые были конечными хотя бы у одного из автоматов А₁ и А₂. Получился новый недетерминированный автомат А. Ясно, что если некое слово распознавалось автоматом А₁ или автоматом А₂, т.е. в орграфе соответствующего автомата существовал путь, размеченный этим словом, из начального состояния в некоторое конечное, то в орграфе автомата А тоже найдется путь из начального состояния в некоторое конечное, также размеченный этим словом. Разумеется, верно и обратное: слово, распознаваемое автоматом А, обязательно распознается одним из автоматов А₁ или А₂. Тем самым, недетерминированный автомат А задает язык .

Рис. 7

Нетрудно показать, что если распознаваем язык L, то распознаваем и язык . Доказательство этого утверждения мы оставляем читателю в качестве несложного упражнения (см. задание 2). Утверждение о том, что пересечение распознаваемых языков L₁ и L₂ — это снова распознаваемый язык, теперь вытекает из уже рассмотренной части утверждений теоремы 1 и довольно известной (и легко доказываемой) формулы теории множеств:

Легко построить автомат, который будет распознавать язык, состоящий ровно из одного слова. Пусть, к примеру, это будет слово а₁а₂...а_n. На рис. 8 приведен недетерминированный автомат, распознающий этот язык.

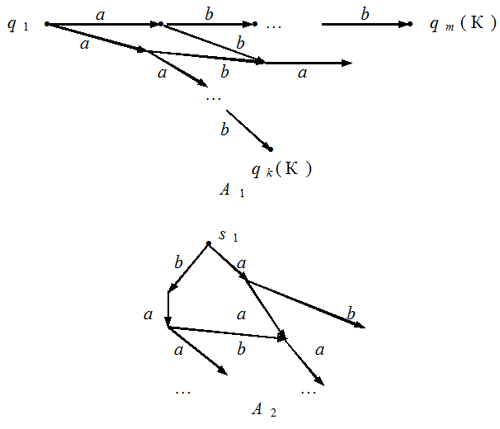
Рис. 8

Из теоремы 1 и сделанного наблюдения легко получить следующее следствие.

Следствие. Любой язык, состоящий из конечного количества слов, распознаваем.

Конкатенацией двух слов а₁а₂...а_n и b₁b₂...b_m называется слово, полученное приписыванием справа к первому слову второго слова, т.е. слово а₁а₂...а_nb₁b₂...b_m. Конкатенацию слов нередко называют умножением слов или сложением; в языках программирования для обозначения операции конкатенации обычно используют знак “+”. Ясно, что операция конкатенации ассоциативна (т.е. удовлетворяет сочетательному закону), но не коммутативна (т.е. не удовлетворяет переместительному закону). Мы будем обозначать конкатенацию умножением и результат называть произведением слов.

Произведением языков L₁ и L₂ называется множество слов, полученных как всевозможные произведения слов языка L₁ на слова языка L₂. Произведение языков L₁ и L₂ будем обозначать как L₁L₂.

Теорема 2. Произведение двух распознаваемых языков является распознаваемым языком.

Доказательство. Пусть L₁ и L₂ — распознаваемые языки, L = L₁L₂. Рассмотрим два недетерминированных автомата А₁ и А₂, первый из которых распознает язык L₁, а второй распознает язык L₂. Пусть они представлены соответствующими орграфами (см. рис. 8). Для доказательства будут важны конечные состояния автомата А₁, поэтому на рис. 8 мы два из них изобразили вершинами q_k и q_m.

Рис. 8

Сделаем теперь столько копий автомата А₂, сколько конечных состояний имеет автомат А₁. Каждое конечное состояние автомата А₁ отождествим с начальным состоянием одной из копий автомата А₂ (см. рис. 9). Получился новый автомат с начальным состоянием q₁ и множеством конечных состояний, которое состоит из конечных состояний всех взятых нами копий автомата А₂. Легко видеть, что построенный автомат распознает слово тогда и только тогда, когда оно является конкатенацией слова, распознаваемого автоматом А₁, и слова, распознаваемого автоматом А₂. Теорема доказана.

Рис. 9

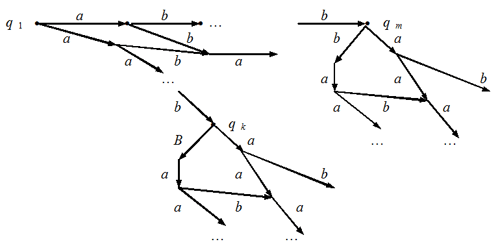
Еще одна операция, которую выполняют над языками, называется итерацией языка. Вот как она определяется. Обозначим через пустое слово, т.е. слово, не содержащее ни одного символа алфавита. Пусть L — некоторый язык. Тогда определим степени языка L, положив L⁰ = {}, L¹ = L, L ^{n + 1} = LLⁿ. Через L* обозначим объединение всех Lⁱ для i 0. Множество L* и называется итерацией языка L.

Теорема 3. Итерация распознаваемого языка является распознаваемым языком.

Доказательство. Пусть L — распознаваемый язык. Рассмотрим недетерминированный автомат А, который распознает язык L. Пусть он представлен соответствующим орграфом (см. рис. 10). Для доказательства будут важны конечные состояния автомата А и предшествующие им, поэтому на рис. 10 мы два конечных состояния изобразили вершинами q_k и q_m.

Рис. 10

Построим новый автомат следующим образом. Во-первых, объявим состояние q₁конечным (если оно уже не было таковым до этого). Во-вторых, ликвидируем все конечные состояния автомата А, кроме состояния q₁, а входящие в них стрелки направим в q₁ (см. рис. 11). Теперь ясно, что слово будет распознаваться новым автоматом тогда и только тогда, когда оно принадлежит некоторой степени языка L, т.е. множество слов, распознаваемых новым автоматом, в точности совпадает с итерацией языка L.

Мы уже отмечали, что любой конечный язык распознаваем. Из рассмотренных теорем немедленно следует, что язык, полученный из конечного набора конечных языков применением конечного числа раз операций объединения, умножения и итерации, будет распознаваемым. Но самое замечательное, что верно и обратное утверждение: если язык распознаваем, то он получается из конечного набора конечных языков применением конечного числа раз операций объединения, умножения и итерации. Это утверждение носит название теоремы Клини — в честь доказавшего ее математика и логика С.Клини.

Рис. 11

Эта теорема отражает важные свойства разработки алгоритмов. Естественно, к примеру, задаться вопросом: почему нет других алгоритмических конструкций, кроме ветвлений, циклов и подпрограмм? Не хватает человеческой фантазии? Но что гласит теорема Клини? Легко видеть, что объединение двух автоматов фактически отвечает за построение программ, реализующих ветвление, — можно исполнять один фрагмент программы, а можно другой. Конечно, здесь еще нет собственно выбора, какой именно фрагмент будет исполняться, но сама программа собрана как бы из двух (или большего числа) частей. Что такое итерация языка? Каждому видно, что это модель циклического алгоритма, когда одна и та же программа повторяется несколько раз. Наконец, что такое произведение языков? Из самого построения соответствующего автомата видно, что второй автомат реализует многократное обращение к одному и тому же комплексу подпрограмм. Так что сама структура распознаваемого языка показывает, что ничего, кроме трех указанных конструкций, не может служить основой для создания языков, управляющих формальными исполнителями.

Конечно, конечный автомат — это весьма простая, хотя и очень важная модель формального исполнителя. Она отличается от других моделей формальных исполнителей, например машины Тьюринга (см. лекцию 2, § 4), хотя бы уже тем, что не имеет памяти, — если мы видим, что автомат пришел после некоторой последовательности команд в некоторое состояние, то мы не можем ничего сказать о том, как это случилось. Мы не можем сохранить никакую информацию о работе автомата. Если же рассматривать автоматы с памятью (а это, кстати, гораздо ближе к любимым нами компьютерам), то их возможности значительно расширяются. И, соответственно, сильно расширяется класс языков, распознаваемых такими автоматами. Но математическая теория автоматов с памятью потребовала бы намного больше места и времени для своего изложения.

Вопросы и задания

1. Постройте недетерминированный автомат, который распознает язык а) {ab, ba}*; б) {ab}*{ba}*; в) {abа}*{bab}*.

2. Докажите, что из распознаваемости языка L следует распознаваемость языка .

3. Пусть L — распознаваемый язык. Построим новый язык L^#, переписав каждое слово языка L “задом наперед” (например, если языку L принадлежало слово abab, то языку L^# будет принадлежать слово baba). Будет ли язык L^# распознаваемым?

4. Пусть А — некоторый конечный алфавит. Будет ли распознаваем язык, состоящий из всех слов-палиндромов над алфавитом А? (Палиндромом называется слово, которое слева направо читается так же, как справа налево.)

§ 6. Формальные грамматики

Как правило, не все возможные слова, построенные из символов заданного алфавита А, входят в тот или иной язык. Известен, пожалуй, единственный случай, когда используемый человеком язык содержит множество всех слов над некоторым алфавитом, — это случай односимвольного алфавита. Такой язык использовался первобытным человеком для счета (единственный знак в алфавите — зарубка); используется он и сейчас при обучении детей счету: здесь знаком алфавита выступает счетная палочка. В технических системах этот язык используется для программного управления шаговыми двигателями — появление единицы означает поворот вала на некоторый фиксированный угол; слово из k единиц воспринимается этим автоматом как команда на последовательное выполнение k поворотов.

Причины, почему не все возможные слова над данным алфавитом входят в язык, могут быть разные. Вот одна из них: любой естественный язык, как бы много слов в нем ни было, всегда конечен, в то время как общее количество слов бесконечно даже для алфавита, состоящего всего лишь из одного знака. Формализованному языку записи натуральных чисел в позиционной нумерации не принадлежат слова, у которых первый знак “0”. Связано это с желанием иметь взаимно-однозначное соответствие между множеством натуральных чисел и их имен — в противном случае пришлось бы договариваться, что, скажем, число 305 имеет еще и такие имена: 0305, 00305, 000305 и т.д.⁴

Таким образом, язык — это некоторое подмножество слов над данным алфавитом. Правила, согласно которым из знаков алфавита образуются слова данного языка, называются грамматикой этого языка. К примеру, алфавит десятичной нумерации — это множество, состоящее из десяти цифр в указанном выше порядке, слово — это запись произвольного числа в десятичной системе счисления, грамматика десятичной нумерации — это правила, согласно которым образуется запись числа, наконец, язык десятичной нумерации — это множество записей всех натуральных чисел.

Как видно из этого рассмотрения, грамматика языка — это правила построения слов не только из символов алфавита, но и уже построенных к этому моменту слов. Иными словами, правила грамматики обычно являются рекурсивными (по-русски — возвратными: как только новое слово построено, оно само может служить “строительным материалом” для построения последующих слов). Отметим, что язык, содержащий бесконечное число слов, может быть построен над конечным алфавитом при помощи конечного числа правил только в том случае, если хотя бы одно из правил рекурсивно. Это обстоятельство учитывается при определении формальной грамматики. Формальной грамматикой Г(A, V, F) называется совокупность конечных множеств V и A, где A — подмножество V, и конечный набор F отображений вида w w’, где w — слово над V\A, а w’ — слово (быть может, пустое, т.е. не содержащее знаков алфавита; пустое слово мы будем обозначать символом “O”) над V. Множество V при этом называется словарем грамматики, множество A — ее терминальным алфавитом, а отображения, принадлежащие F, называются продуционными правилами. Будем говорить, что слово w' над алфавитом V непосредственно продуцируется из слова w в грамматике Г(A, V, F), если w и w’ представимы соответственно в виде xuy и xvy для подходящих x и y, а uv — некоторое правило из F. Слово w’ над V называется продуцируемым из слова w (мы будем записывать это как w w’), если существует конечная последовательность слов w₀, w₁, ..., w_n, для которой w₀ = w, w_n = w’ и при i > 0 каждое w_i непосредственно продуцируется из w_i-1. Формальным языком, порожденным над W грамматикой Г(A, V, F), называется множество слов, продуцируемых из символов фиксированного подмножества W, содержащихся в словаре V, и состоящих только символы терминального алфавита A.

К примеру, формальный язык, состоящий из всех слов над односимвольным алфавитом, скажем, {x} (о таком языке речь шла выше), порождается над {y} следующей грамматикой Г(A,V,F), где A = {x}, V = {x, y}, F = {y xy; y O}. Здесь правило y xy рекурсивно и обеспечивает “производство” бесконечного числа слов, а правило y O обеспечивает наличие слов над терминальным алфавитом, т.е. непустоту языка.

Другой пример в своей основе принадлежит одному из основателей теории формальных языков Н.Хомскому. Поскольку автор англоязычен, то речь в примере идет об английской грамматике. Нетерминальные символы словаря представляют основные грамматические понятия: подлежащее, сказуемое, определение, существительное, глагол, артикль, прилагательное, наречие. Вот эти символы:

(N) — существительное;

(V) — глагол;

(T) — артикль;

(ADJ) — прилагательное;

(ADV) — наречие;

(NP) — группа подлежащего;

(VP) — группа сказуемого;

(AP) — группа определения;

(S) — предложение.

Терминальный алфавит состоит из слов английского языка. Мы, разумеется, для нашего примера возьмем не весь словарный запас английского языка, а ограничимся следующими пятнадцатью словами: A = {a_; ball_; book_; boy_; early_; good_; is_; is_not_; reads_; plays_; quickly_; red_; stands_up_; the_; well_} — с пробелом (обозначенным как _)
в конце каждого слова.

А вот множество правил:

Вот, например, как можно получить предложение “a_boy_stands_up_”:

(S)(NP)(VP)(NP)(V)(T)(AP)(VP)(T)(N)(VP)(T)boy_(VP) a_boy_(VP) a_boy_stands_up_

Аналогично можно получить предложение “a_good_boy_reads_a_book_” или предложение “the_ball_is_red_”. Все эти предложения не только грамматически правильны, но и осмысленны. Однако может получиться грамматически правильное, но бессмысленное предложение. Например, “a_ball_reads_early_”. Это наблюдение может показаться читателю той ложкой дегтя, которая портит бочку меда. Но отметим: в постановке задачи определения формальной грамматики никто ведь и не требовал, чтобы получающиеся лингвистические структуры были осмысливаемы.

Нас в этой главе интересуют языки, распознаваемые конечными автоматами. Естественны поэтому два вопроса: каждый ли распознаваемый язык может быть определен подходящей грамматикой, и какой должна быть грамматика, чтобы определяемый ею язык был распознаваемым? Ответы на оба вопроса математиками были получены, а именно, язык распознаваем некоторым конечным автоматом тогда и только тогда, когда он порождается формальной грамматикой с продуционными правилами вида

x wy или z v,

где x, y, z — нетерминальные символы, зато w и v — слова (быть может, пустые) над терминальным алфавитом. Грамматики с такими продуционными правилами получили специальное название — праволинейные грамматики.

Всякий компьютер — это, разумеется, некий конечный автомат (правда, обладающий еще и памятью, о чем мы выше упоминали), так что для управления им годятся соответствующие формальные языки (более широкие, чем просто для конечных автоматов). Фактически это и есть языки программирования. Но описывать язык программирования в указанной выше форме не так уж удобно. Поэтому имеются различные упрощения и сокращения формы записи продуционных правил. Одним из широко применяемых способов записи является так называемая “форма Бэкуса — Науэра”, или, по-другому, бэкусова нормальная форма (сокращенно БНФ). При записи БНФ используются следующие соглашения: определяемое понятие — нетерминальный символ — заключается в угловые скобки (например, <буква>); символ “::=” читается словом “есть”; символ “|” читается словом “или”. Это означает, что в этом случае записано сразу несколько продуционных правил с одной и той же левой частью. Приведем пример определения понятия <идентификатор>. (При определении понятия <буква> мы, по вполне понятным причинам, не станем перечислять все буквы алфавита.)

<идентификатор>::=<буква>|<буква><последовательность символов>

<последовательность символов>::=<буква>|
<цифра>|<буква><последовательность символов>
|<цифра><последовательность символов>

<буква>::=a|b|c|d|...|x|y|z

<цифра>::=0|1|2|3|4|5|6|7|8|9

Из этого определения видно, в частности, что всякий идентификатор обязательно начинается с буквы (ограничения на длину идентификатора мы не рассматриваем).

Из этого примера видно, что формальные грамматики являются весьма удобным средством описания языка, может быть, даже более удобным, чем описание с помощью операций. Однако запись “большого” языка через операции над более простыми языками позволяет легче конструировать распознающий этот язык автомат. По формальной грамматике это сделать сложнее, хотя и для решения этой задачи математиками создан соответствующий алгоритм.

Вопросы и задания

1. По неформальному описанию (в тексте параграфа) грамматики языка записи натуральных чисел постройте формальную грамматику этого языка. Будет ли она праволинейной?

2. а) Найдите еще какой-либо путь порождения фразы “a_boy_stands_up_”.

б) Найдите какой-либо путь порождения фразы “the_ball_is_red_”.

в) Найдите какой-либо путь порождения фразы “a_ball_reads_early_”.

г) Какой из двух языков — русский или английский — представляется вам более формализованным и почему?

3. а) Является ли грамматика описания понятия “идентификатор” праволинейной?

б) Две грамматики называются эквивалентными, если они определяют один и тот же формальный язык. Покажите, что существует праволинейная грамматика, эквивалентная предложенной выше грамматике описания понятия “идентификатор”.

4. Грамматика называется леволинейной, если все ее продуционные правила имеют вид

x yw или z v,

где x, y, z — нетерминальные символы, а w и v — слова (быть может, пустые) над терминальным алфавитом. Является ли язык, определенный леволинейной грамматикой, распознаваемым?

5. Пусть задан терминальный алфавит А = {a, b}; грамматика содержит три продуционных правила:
x aby, y bx, x a.

а) Какой язык порождает эта грамматика?

б) Постройте автомат, распознающий этот язык.

¹ Напомним, что граф — это совокупность точек, называемых вершинами, и линий, соединяющих некоторые из вершин. Если на линиях, соединяющих вершины, указано направление, то граф называется ориентированным (сокращенно орграфом), а линии называются его дугами.

² Как мы видим, алгоритмы для недетерминированных автоматов не только не обладают свойством детерминированности, но могут не обладать и свойством результативности. От этого, однако, они не перестают быть алгоритмами.

³ Впрочем, мы не утверждаем, что этот тезис справедлив для всех ораторов.

⁴ Каждый знает, но мало кто задумывался, что в аналогичной ситуации с десятичными дробями без подобной договоренности не обойтись — мы принимаем, например, что для числа 1.5 есть еще имена 1.50, 1.500, 1.5000 и т.д. Впрочем, для того же числа есть еще и такое имя: 1.4999999... Причина столь большого количества синонимов (т.е. имен с одним и тем же значением) кроется в особенностях операций над действительными числами.