Вы - -й посетитель этой странички
Примерное содержание компьютерного задачника по информатике
Е.В. Андреева
МоскваВведение
В прошлом номере “Информатики” было рассказано о некоторых аспектах автоматизации проверки учебных и олимпиадных задач по информатике. После решения технических проблем на первый план выходят проблемы наполнения содержанием созданной программной оболочки. То есть прежде всего необходимо определить, какими возможностями должна обладать подобная система, для того чтобы ее можно было бы эффективно использовать в процессе обучения, в частности, программированию, какие задачи и задания она должна содержать и как в дальнейшем пополнять и изменять набор имеющихся задач, как эти задачи должны проверяться и оцениваться и, в конце концов, какую информацию по результатам проверки и в каком виде должна предоставлять система преподавателю. В данной статье сконцентрируем внимание на наиболее сложной из перечисленных проблем - формировании наборов задач для различных категорий учащихся.
Потребности создания компьютерного задачника для различных категорий учащихся
В настоящее время в нашей стране с точки зрения обучения программированию можно выделить несколько категорий учащихся. Во-первых, это ученики основной школы, курс информатики в которой преподается за счет часов вариативной части Базового учебного плана [1]. Министерством образования РФ рекомендован “Обязательный минимум содержания образования”, который имеет два уровня. Уровень А определяет содержание образования по информатике, обязательное для всех учащихся общеобразовательных школ. Согласно ему учащиеся должны освоить реализацию основных алгоритмических конструкций в одном из языков программирования, познакомиться с простыми типами данных и массивами (таблицами) как способом представления информации. То есть при составлении задачника для основной школы внимание должно уделяться преимущественно задачам, способствующим отработке применения основных алгоритмических конструкций с использованием простых типов данных и массивов. Такие задачи могут составлять первую часть задачника по началам программирования. Автоматическая проверка подобных задач возможна, однако ее одной в данном случае явно не достаточно. Обучение правильному применению тех или иных алгоритмических конструкций требует постоянного контроля со стороны преподавателя. Кроме того, задания этого уровня настолько просты, что “ручная” проверка, в том числе и листингов программ, не занимает много времени. Однако при организации занятий именно для таких категорий учащихся удобно использовать систему автоматического тестированиятеоретическихзнаний.
Уровень Б соответствует углубленного курса информатики, который преподается в основном в физико-математических школах. Помимо перечисленных выше знаний в области программирования, учащиеся таких школ должны уметь оперировать всеми основными типами данных одного из современных алгоритмических языков, включая объекты, использовать при разработке программ процедуры, функции и операции над объектами и разрабатывать программы методом последовательной детализации. В требованияхк результатам обучения на таком уровне говорится, что учащиеся должны уметь расписывать на языке программирования типовые алгоритмы, такие,как: поиск минимального и максимального элемента в массиве, упорядочивание элементов массива, определение количества слов в тексте - и т.д. Данныетребования фактически и определяют содержание задачника для такой категории учащихся. Характер исложность этих задач таковы, что автоматическая ихпроверка может существенно повысить эффективность занятий по информатике.В последнюю категорию можно выделить участников олимпиад по информатике. Задачи, предлагаемые на олимпиадах, охватывают различные разделы информатики и программирования. Тем не менее их темы, а также основные алгоритмы решения возможно формализовать. Помимо традиционных учебных тем, зачастую эти задачи используют идеи и приемы, применяемые в профессиональном программировании, например, идеи шифрования,принципы организации поиска в большом объеме инфор-мации, синтаксический и семантический разбор выражений, методы решения NP-полных задач и т.д. Большинство задач, предлагаемых на олимпиадах, после их окончания доступны вместе с набором тестов и программами для проверки правильности выходных данных программ участников на этих тестах. Поэтому включение подобных задач в компьютерный задачник существенно облегчено. В результате такой задачник может оказать неоценимую помощь при подготовке к новым соревнованиям.
При создании части компьютерного задачника, предназначенной для обучения основам программирования,можно использовать задачи по программированию, предлагаемые в [2, 3], а также в первой главе [4]. Перечислим основные классы и приведем примеры задач, которые должны присутствовать в данной части задачника.
1. Задачи на операции ввода и вывода .
Подобный класс задач важен особенно для компьютерного задачника, так как, выполняя подобные задания, учащиеся смогут понять формальные требования, которые предъявляются к программам при их автоматическом тестировании. Пример 1 .Написать программу, которая запрашивает имя пользователя с помощью приглашения
Введите Ваше имя:
вводит имя с клавиатуры и выдает на экран приветствие
Здравствуйте, <
введенное имя>! Проверку подобных задач можно проводить, сравнивая правильный ответ на тест с выдачей программы учащегося с точностью до пробелов и символов перевода строки. 2. Задачи на оператор присваивания. Несмотря накажущуюся простоту, в данный раздел могут быть включены задачи различной сложности. В частности, требованиене использовать в программе условный оператор и операторы цикла переводит ряд элементарных задач в задачи повышенной сложности. Такое ограничение с методической точки зрения можно рассматривать как работу с исполнителем, имеющим ограниченный набор команд.Пример 2.
Обозначим дни недели числами от 1 — понедельник до7 — воскресенье, соответственно. Программа должна вводить с клавиатуры два натуральных числа: 0 < N < 32 — число в текущем месяце и 0 < M < 8 — день недели для первого числа в текущем месяце. Вывести на экран число от 1 до 7, обозначающее, на какой день недели приходится число N.
Пример 3.
Bвести с клавиатуры 2 целых числа: 0 <= H < 12, 0 <= M < 60, указывающие момент времени H часовM минут. Определить и вывести на экран наименьшее число полных минут, которое должно пройти до того момента, когда часовая и минутная стрелки на циферблате совпадут.
Пример 4.
По введенному с клавиатуры вещественному числу x вывести на экран целочисленное значение функции sgn x.
Решения этих и других подобных задач можно найтив [3]. При решении данного класса задач учащиеся осваивают основные операции и функции изучаемого языка программирования. Особое внимание при этом уделяется арифметике остатков, знания по которой, как показывает практика, у учащихся недостаточны. Однако именно операции целочисленной арифметики имеют важную роль в программировании.
3. Задачи на логические выражения . При изучении логических выражений полезным является выполнение следующего практического задания.Пример 5.
Каждому учащемуся выдается индивидуальный рисунок. То есть на координатной плоскости изображены линии, описываемые уравнениями окружности, прямой, парабол
y = f(x) и x = f(y ),
ромба, прямоугольника и т.п. (сложность рисунка зависит от категории учащихся). Несколько областей, ограниченных этими линиями, заштрихованы. Требуется описать всю заштрихованную часть плоскости с помощью одного логического выражения. Программа должна запрашивать с клавиатуры координаты ( x, y) некоторой произвольной точки плоскости и определять, принадлежит ли точка с координатами ( x, y) заштрихованной области. Ответвыдать в следующем виде: true, если точка с координатами ( x, y) принадлежит заштрихованной области, иfalse, если точка с координатами ( x, y) не принадлежит ей. При выполнении задания от учащихся следует требовать, чтобы для описания каждой области была введена своя логическая переменная, что упрощает процесс отладки и поиска ошибок при приеме задания. Основное логическое выражение конструируется только из таких переменных. Имена переменных должны быть мнемоничны. Например: InCircle1, UpperLine1.
Примечание. В СУНЦ МГУ автоматическая проверка данного задания производится следующим образом. Программа учащегося конвертируется в функцию с логическим результатом без какого-либо собственного вывода на экран, значения этой функции вычисляются для части плоскости, изображенной на рисунке, и выдаются на графический экран (значению true соответствуетбелый цвет пикселя, false — черный). Далее не составляет труда сравнить рисунок на экране с исходным. Подробнее об организации подобного задания, его проверке и вариантах задач можно будет прочитать в следующем номере “Информатики”. 4. Условный оператор . Цель данного раздела задачника — научить учащихся составлять алгоритмы с использованием простых и вложенных операторов условия и выбора. Пример 6.
По введенным с клавиатуры значениям целочисленных переменных y (номер года), m (номер месяца), d (номер дня) определить — правильная эта дата или нет. Если правильная, то выдать на экран дату следующего дня в формате d.m.y, в противном случае вывести фразу:
Дата некорректна.
Пример 7.
Для введенных с клавиатуры действительных значений параметров a, b, d решить уравнение относительно x: ax 3 + bx 2 + dbx + d 3 a = 0. Упорядочить полученные значения для x по возрастанию и выдать каждое изних в новой строке экрана с точностью до четырех значащих цифр после точки. Если решение отсутствует, то выдать фразу:
Нет решения,
а в случае бесконечного множества решений:
x — любое.
5. Операторы цикла .
Основные классы задач, относящиеся к данному разделу, это задачи на обработку числовых последовательностей без использования массивов для их хранения, включая нахождение НОД или НОК для последовательностей натуральных чисел, задачи на рекуррентные соотношения и суммирование числовых рядов. В последнем случае важное значение имеет эффективность программы.Так, при суммировании рядов, аналогичных рядам Тейлора, операции возведения в степень или циклы для вычисления целочисленной степени или факториала применяться не должны. Вместо этого каждое следующее слагаемое должно выражаться через предыдущее с помощью основных арифметических операций. Данный факт следует учитыватьпри автоматическом тестировании подобных программ.Пример 8.
С клавиатуры вводится последовательность различных натуральных чисел, за которой следует 0. Определить и вывести на экран значение наименьшего и наибольшего членов последовательности, а также их среднее арифметическое. Приведем также менее стандартные примеры задач, использующих операторы цикла.
Пример 9.
Вычислить значение следующего выражения с макси-мально возможной точностью:
С клавиатуры вводится действительное число 0 < e < 1.Вычислить следующую сумму, не учитывая слагаемые,меньшие e:
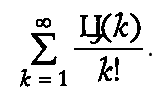
Здесь Ц(
k) — количество цифр в числе k.Пример 11.
По введенному действительному значению радиуса круга (0 <= R <= 100 000) вычислить количество точек с целочисленными координатами, попадающих в круг радиуса R с центром в начале координат. Функции действительных переменных, такие, как sin, cos, sqrt, не использовать.
Пример 12.
Вывести логическое значение true или false, взависимости от того, можно или нельзя представитьданное число n в виде суммы двух квадратов. Неиспользовать вложенные циклы.
Пример 13.
Подсчитать число пятниц, приходящихся на 13-е числав XX веке, если известно, что 13 января 1901 года было воскресенье.
6. Простейшие операции над одномерными массивами .
Цель данного раздела задачника — научить учащихся правильно описывать, вводить, выводить и обрабатывать одномерные массивы. Стандартными в данном разделе следует считать задачи на поиск максимального и минимального элементов, сдвиг и перестановку элементов массива и, наконец, его сортировку. Покажем также нетривиальные задачи, при решении которых используются одномерные массивы.Пример 14 (см. [13]).
Вычислить по схеме Горнера значение полинома
![]()
Пример 15 (см. [5]).
С клавиатуры вводятся два целых числа 0 < m,n < 101, а затем m + n элементов целочисленных элементов массива, каждый из которых по модулю не превосходит 32 767. Не используя дополнительных массивов, требуется переставить местами первые n и последующие m элементов массива. Вывести на экран полученный в результате перестановки массив, разделяя его элементы пробелами.
Пример 16.
С клавиатуры вводится некоторый текст на английском языке, заканчивающийся точкой. Распечатать сведения о том, сколько каких английских букв в тексте.Учесть, что в тексте могут встречаться символы, отличные от латинских букв. Прописные и строчные буквы при подсчете не различать. Вывести на экран 26 чисел, каждое в новой строке, первое из которых соответствует количеству букв a в тексте, второе — букв b и т.д.
7. Процедуры и функции .
Наиболее удачным примером для применения процедур на начальном этапе обучения программированию являются задачи сортировки и поиска [3, 6]. Другой класс задач, требующий естественного применения процедур и функций, — простейшие численные методы интегрирования, а также решение трансцендентных уравнений методами деления пополам, хорд, касательных или итераций.Содержание тематической части задачника
После изучения основ программирования на любом алгоритмическом языке круг решаемых задач существенно зависит от категории учащихся. Поэтому при наполнении данной части задачника следует учитывать потребности того или иного учебного заведения. Тематические подборки задач можно найти в [3, 4], а также использовать задачи различных олимпиад по программированию и информатике, в частности, опубликованные в [7, 8, 9, 10, 11, 12]. Сформулируем лишь некоторые из тем, задания по которым могут быть полезны для широкого круга учащихся.
1. Задачи по системам счисления . Предлагаемый в [13] набор задач позволяет не только овладеть данным разделом теоретической информатики, но и усовершенствовать технику программирования.
2. Задачи на “длинную арифметику” [13]. Помимо традиционных задач на сложение, вычитание, умножение и целочисленное деление “длинных” чисел, в данный раздел можно включить различные задачи, получить точный ответ в которых можно, лишь самостоятельно реализовав те или иные арифметические операции.
3. Задачи на использование динамических структур данных, таких, как: список, стек, очередь, дерево, сбалансированное дерево бинарного поиска — и т.п.
4. Алгоритмы на графах . В частности, наиболее часто в программировании встречаются следующие задачи: обход графа в глубину и в ширину, подсчет компонент связности, построение минимального остовного дерева, поиск кратчайшего пути в графе, нахождение эйлерова цикла, задача коммивояжера (гамильтонов цикл), задачи о размещениях [7].
5. Целочисленные задачи линейного программирования . В том числе поиск наибольшего паросочетания в двудольном графе, задача о назначениях, задача о максимальном потоке, общая задача линейного программирования, при решении которой используется симплекс-метод.
6. Задачи, решаемые методом динамическогопрограммирования [14].
7. Задачи на полный перебор вариантов, при решении которых используется перебор с возвратом с применением метода ветвей и границ и других методов сокращения перебора. В частности, задачи на программирование игр и головоломок с использованием отсечений [14].
8. Комбинаторные задачи . Для каждой из основных комбинаторных конфигураций — множество всех подмножеств, сочетания, перестановки, размещения и т.п. — можно поставить следующие задачи. Для заданных входных параметров подсчитать количество всех возможных конфигураций того или иного типа, сгенерировать все конфигурации соответствующего типа, определить конкретную конфигурацию по ее номеру в лексикографическом порядке конфигураций и, наоборот, по конфигурации определить ее номер, для любой заданной конфигурации построить следующую в лексикографическом порядке [15].
9. Задачи вычислительной геометрии и компьютерной графики [16, 17].
10. Задачи по теории формальных грамматик и конечных автоматов . Начиная с проверки правильности записи арифметических выражений и подсчета их значений до элементов интерпретации и компиляции программ [3, 5].
11. Задачи криптографии [18].
Тесты по теоретической информатике
Компьютерный задачник логично использовать и для классического тестирования, причем в любой области знаний. Признавая очевидные преимущества проведения тестирования (возможность одновременно оценить большое количество учащихся по достаточно широкому кругувопросов учебного курса), многие критики отмечают слишком узкий круг знаний и умений, которые можно проверить в тестовой форме. Тем не менее, по мнению психологов [19], при грамотном подходе именно тесты по информатике могут помочь раскрыть уровень развития способностей учащихся к выполнению операций содержательно-логического мышления. Несмотря на критические замечания относительно тестирования как способа проверки знаний учащихся, бесспорным можно считать тот факт, что с помощью тестирования можно покрайней мере выявить пробелы в знаниях.
На наш взгляд, на современном этапе развития преподавания информатики тестированию, особенно на всероссийском уровне, могут подвергаться лишь знания по ее теоретическим основам. А именно следующие разделы содержания образования по информатике: понятие информации и способы ее представления, системы счисления и формальная логика, а также основы алгоритмизации. Большинство тестов, опубликованных нанастоящий момент, в том числе по этим темам, подвергаются справедливой критике.
Каким же требованиям должен отвечать качественный, профессионально разработанный тест? Во-первых,такой тест должен быть надежным. То есть результат его выполнения не должен носить случайный характер. Вероятность “угадывания” в надежном тесте исключена. Надежность теста характеризуется последовательностью, устойчивостью оценок, получаемых с его помощью. Во-вторых, качественный тест должен быть валидным. То есть он должен измерять уровень развития именно тех умений и навыков, которые предполагали измерять его составители. Таким образом, при профессиональном тестировании можно быть уверенным, что знания и умения будут достойно оценены. Разработка тестовых заданий требует не только глубоких знаний предмета, не только дидактического опыта, но и специальных знаний и навыков в области теории и практики составления самих тестовых заданий. Эти знания и умения позволяют тестировать не столько
декларативный уровень поверхностных знаний, основанный лишь на ассоциативных связях ключевых слов, но и более глубокий уровень реально ценных операциональных знаний,позволяющий реально использовать полученные знанияна практике. Профессионально составленные тестовые задания также содержат поверхностные ассоциативные связи, но в качестве провокационных мнимых правильных ответов — дистракторов.Наиболее часто встречающаяся ошибка при составлении ответов на тестовые задания со множественными вариантами ответа состоит в непродуманных дистракторах. Они либо явно неправдоподобны и не соответствуют элементарному здравому смыслу, либо просто выглядят значительно менее привлекательно, нежели правильный ответ. Включение же тестовых заданий в компьютерный задачник частично эти проблемы решает, так как для части вопросов варианты ответов можно не указывать вовсе, ожидая, что ответ будет введен пользователем самостоятельно.Тем не менее приведем примеры нескольких, на наш взгляд, удачно составленных тестовых заданий по теоретической информатике. Правильные ответы в каждомиз вопросов выделены жирным шрифтом.
Пример 17 . (Олимпиада по базовому курсу информа-тики, Пермская обл., 2001 г.)
Сообщение на языке племени Мульти содержит 64 символа, что составляет 1/32 часть килобайта. Сколько символов содержит алфавит племени Мульти?
1) 128. 2) 16. 3) 32. 4) 8. 5) 64.
Пример 18. (Олимпиада по базовому курсу информа-тики, Пермская обл., 2001 г.)
Два исполнителя — Мульти и Пульти проставляют 0 или 1 в каждую из имеющихся в их распоряжении клеточек. Мульти может закодировать таким образом 64 символа, а Пульти — в 2 раза меньше. Выбрать верное высказывание:
1) В
распоряжении Мульти в два раза больше клеточек, чем у Пульти.
2) В распоряжении Мульти в два раза
меньше клеточек, чем у Пульти.
3) В распоряжении Мульти на 32 клеточки больше,чем у
Пульти.
4) В распоряжении Мульти на 1 клеточку меньше,чем у
Пульти.
5)
В распоряжении Мульти на 1 клеточку больше, чем у
Пульти.
Пример 19.
Запись числа в четверичной системе счисления содержит 8 цифр. Из скольких цифр будет состоять запись того же числа в восьмеричной системе счисления?
1) 4 2)5 или 6 3) 6 4) 8 5) 16.
Пример 20.
Для записи целых чисел в системе счисления “8—4—2” в младшем разряде используются цифры двоичной системы счисления; в следующем разряде — цифры системы счисления с основанием 4; в третьем разряде — системы счисления с основанием 8 и т.д. Чему равно максимальное трехзначное число этой системы счисления в десятичной системе?
1) 842. 2) 731 3) 69. 4) 63. 5) 473.
Пример 21. (Олимпиада по базовому курсу информа-тики, Пермская обл., 2001 г.)
Выбрать высказывание, для которого будет истинно следующее логическое выражение:
![]()
1) Хотя
бы одно из чисел X, Y, Z положительно.
2) Хотя бы одно из чисел X, Y,
Z отрицательно.
3) Хотя бы одно из чисел X, Y,
Z не является
положительным.
4) Только одно из чисел X, Y,
Z является отрицательным.
5) Только
одно из чисел X, Y, Z является неположительным.
Пример 22 .
В булевой
алгебре множеств, в частности, существуют следующие операции над множествами:
объединение, пересечение, дополнение и симметрическая разность. Какая из
следующих пар операций НЕ является полной для всех приведенных (то есть через
них нельзя выразить остальные две):
1) Объединение и дополнение.
2)
Пересечение и дополнение.
3) Объединение и симметрическая разность.
4)
Пересечение и симметрическая разность.
5)
Объединение и
пересечение.
Пример 23.
Процедура сортировки методом “прямого выбора”была применена к массиву 7 3 9 1 2 6 5 0.
Как
будетвыглядеть этот массив после трех итераций алгоритма?
1)
0 1 2 3 9 6 5 7.
2) 0 1 2 7 3 9 6 5.
3) 3 7 9 1 2
6 5 0.
4) 5 3 0 1 2 6 7 9.
5) 3 1 2 5 0 6 7 9.
Пример 24.
I. Существует сортировка, у которой и число сравнений, и число присваиваний меньше, чем O(N 2 ).
II. Существует сортировка, у которой число присваиваний даже в худшем случае составит O(N ) для произвольного массива.
III. Существует сортировка, у которой число cравнений даже в худшем случае O(N ) для произвольного массива.
Какие из этих высказываний справедливы?
1) I, II.
2) II, III.
3) I, III.
4) Все
верны.
5) Правильного ответа среди перечисленных выше нет.
Пример 25.
Дополнительный код числа —100 в 8- и 16-разрядных ячейках выглядит, как
1)
11100100 и 1000000001100100.
2) 10011011 и 1111111110011011.
3) 10011011 и
0000000010011011.
4)
10011100 и 1111111110011100.
5) 10011100 и 0000000010011100.
Работа по совершенствованию и расширению задачника в настоящее время продолжается. Желающие обменяться опытом по созданию подобных задачников иливнести свои пожелания и предложения могут обращаться к автору по адресу helena.1september@gmail.com.
Литература
1. Базовый учебный план. Приказ Министерства образования РФ № 322 от 09.02.1998.2. Пильщиков В.Н. Сборник упражнений по языку Паскаль. М.:Наука, 1989.
3. Андреева Е., Фалина И. Турбо-Паскаль в школе. М.: Изд-во Бочкаревой Н.Ф., 1998.
4. Абрамов С.А., Гнездилова Г.Г. и др. Задачи по программированию. М.: Наука, 1988.
5. Шень А. Программирование: теоремы и задачи. М.: МЦНМО,1995.
6. Окулов С.М. Сортировка и поиск. Конспекты занятий. Информатика, № 33, 35, 36/2000.
7. Окулов С.М., Пестов А.А., Пестов О.А. Информатика в задачах. Киров: Вятский государственный педагогический университет, 1998.
8. Брудно А.Л., Каплан Л.И. Московские олимпиады по программированию. М.: Наука, 1990.
9. Кирюхин В.М., Лапунов А.В., Окулов С.М. Задачи по информатике. М.: ABF, 1996.
10. Чернов А.В., Андреева Е.В., Панкратьев Е.В. и др. Московские студенческие олимпиады по программированию. М.: Изд. отдел факультета ВМиК МГУ им. М.В. Ломоносова, 1999.
11. Беров В.И., Лапунов А.В. и др. Особенности национальных олимпиад по информатике. Киров: Триада-С, 2000.
12. Андреева Е.В. Задачи XIII Всероссийской олимпиады по информатике. Информатика, № 19/2001.
13. Андреева Е., Фалина И. Системы счисления и компьютерная арифметика. М.: Лаборатория базовых знаний, 2000.
14. Андреева Е.В. Еще раз о задачах на полный перебор вариантов. Информатика, № 45/2000.
15. Окулов С.М. Комбинаторные задачи. Информатика, № 7, 10,13/2000 .
16. Препарата Ф., Шеймос М. Вычислительная геометрия. Введение. M.: Мир, 1989.
17. Боресков А.В., Шикин Е.В., Шикина Г.Е. Компьютерная графика: первое знакомство. М.: Финансы и статистика, 1996.
18. Введение в криптографию. Под ред. Ященко В.В. М.:МЦНМО, 1998.
19. Шмелев А.Г. Тесты по информатике. Послесловие. Информатика, № 44/1999.