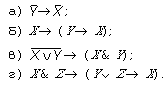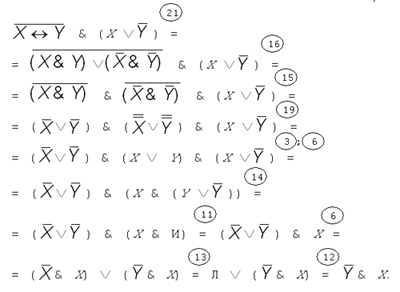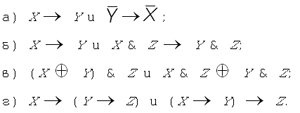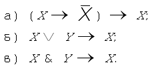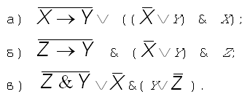Курсы повышения квалификации

Математические основы информатики

А.Г. Гейн

Учебный план

Лекция 5. Логические модели в информатике

Уже много сказано о возможностях компьютеров и применяемых информационных технологий, чтобы каждый понял, какую неоценимую помощь может оказывать компьютер в предоставлении и обработке информации. Однако за человеком остается право (и обязанность) делать выводы на основе предоставляемой информации и принимать соответствующие решения. Конечно, иногда мы говорим, что решение принимает компьютер. Например, если компьютер, управляя каким-либо автоматом, получает от датчиков этого автомата информацию об опасности его разрушения в тех условиях, в которых он оказался, то компьютер может “принять решение” об эвакуации автомата из этой обстановки. Но каждому ясно, что на самом деле это решение было заранее запрограммировано человеком и компьютер, как обычно, безоговорочно следует инструкции.

Принятие решения — это в конечном счете всегда прерогатива человека. Во-первых, потому что любая информация в компьютере лишь модельно отражает реальную действительность, и, следовательно, принимаемое компьютером решение может оказаться неадекватным сложившейся ситуации.
В вышеприведенном примере вполне вероятна ситуация, что автомат должен погибнуть, чтобы предотвратить большее несчастье. Во-вторых, передать компьютеру право принимать решения — значит вверить судьбу человечества электронике. И хотя сегодня бунт роботов — это все еще удел фантастических произведений, в их основе лежит именно предположение о предоставлении компьютеру права принимать решения наравне с человеком.

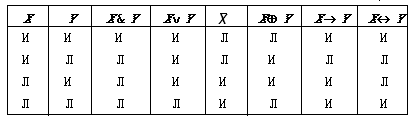
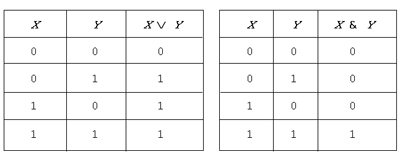
Тем не менее помощь компьютера в решении человеком информационных задач намного бы выросла, если бы компьютер “научился” предлагать человеку на выбор обоснованные варианты возможных решений. Но для этого надо научить компьютер делать выводы из имеющейся информации. Иными словами, надо в компьютере смоделировать процесс рассуждений, которые проводит человек.
О тех подходах к решению данной проблемы, которые сегодня разрабатываются в информатике, и пойдет речь в этой лекции.

Первым, кто предпринял удачную попытку построить модель человеческих рассуждений, был, по мнению историков науки, древнегреческий ученый Аристотель. Именно он сформулировал первые законы рассуждений, заложив основы новой науки, названной им логикой. В дальнейшем вклад в эту науку вносили психологи и философы, лингвисты и математики. У этой науки появились разные направления исследований, она разделилась на ряд областей, одна из которых называется формальной, или математической, логикой. Более того, происходила не только специализация исследований внутри логики, но и расширение сферы исследований на всю интеллектуальную деятельность человека. Как человек распознает предметы и явления, как происходит обучение и самообучение, как вырабатываются стратегии в реальной жизни или играх, каковы механизмы стихосложения и сочинения музыки — все это стало предметом исследований ученых. А модели, создаваемые в результате таких исследований, стали называть моделями искусственного интеллекта.

§ 16. Элементы логики высказываний

Психологи давно установили, что мыслительная деятельность человека всегда осуществляется посредством какого-либо языка. Использование языка придает мыслительной деятельности форму рассуждений. Что такое рассуждение? Ответить можно так: это последовательность вопросов, задаваемых самому себе или собеседнику, и ответов на них.

Вопросы могут быть разного типа. Можно спросить: “Сколько существует простых чисел?” Ответом служит утверждение: “Простых чисел бесконечно много”. Можно спросить: “Как найти тысячное простое число?” Ответом будет алгоритм, позволяющий вычислить требуемое простое число. Информацию, содержащуюся в ответе на первый вопрос, обычно относят к декларативному типу, а информацию, содержащуюся в ответе на второй вопрос, — к процедурному.

Напомним, что среди свойств алгоритмов, обсуждавшихся нами в лекции 3, есть, например, результативность и правильность. А вот информацию, представленную декларативно, можно, пожалуй, оценить только с одной позиции — истинна она или ложна.

Повествовательное предложение, в отношении которого имеет смысл говорить о его истинности или ложности, называется высказыванием. Такое определение высказыванию дал Аристотель, который, как было сказано выше, считается основоположником логики как науки.

Рассмотрим следующие предложения.

1. Число иррационально.

2. Число рационально.

3. Любое натуральное число х рационально.

4. Любое число х рационально.

5. Существует число х, которое иррационально.

6. Число х рационально.

7. Если число х иррационально, то число х + 1 тоже иррационально.

8. Число называется рациональным, если оно равно отношению целого числа к натуральному.

9. Верно ли, что число иррационально?

10. Докажите, что число иррационально.

Первые пять предложений, очевидно, являются высказываниями, причем первое, третье и пятое истинны, а второе и четвертое ложны. Два последних предложения не являются высказываниями, поскольку они вовсе не повествовательные: одно из них вопросительное, а другое — побудительное. Предложение 8 не является высказыванием, поскольку об его истинности говорить бессмысленно — оно лишь определяет новое понятие через ранее введенные.

В повествовательном предложении 6 истинность заключенной в нем информации зависит от значения переменной х: при одних ее значениях утверждение окажется истинным, при других — ложным. Так что это предложение нельзя отнести к высказываниям (мы рассмотрим подобные утверждения несколько позже). Точно так же переменную х содержит предложение 7, поэтому и его не следует относить к высказываниям. Но если задуматься о смысле этого предложения, то станет ясно, что оно истинно при любом значении переменной х.

Пример предложения 7 показывает, что данное Аристотелем объяснение, что такое высказывание, не является, строго говоря, определением. Более того, оно фактически перекладывает на плечи других научных дисциплин — математики, физики, химии, биологии, истории (список вы легко продолжите сами) — саму проблему получения ответа на вопрос, будет ли истинным то или иное утверждение. И вот если ответ на такой вопрос будет получен, то это утверждение получит право называться высказыванием.

Впрочем, для некоторых утверждений ответ об их истинности или ложности нельзя получить никакими средствами. Вот одно из таких утверждений: “Это предложение ложно”. Если предположить, что само это утверждение истинно, то оно обязано быть ложным. Если же считать, что утверждение ложно, то оно обязано быть истинным. Выявление и недопущение в рассуждениях подобных внутренне противоречивых утверждений — тоже одна из задач логики.

Оставляя другим наукам отвечать на вопрос об истинности конкретного утверждения, логика интересуется, как из набора истинных утверждений можно получать новые истинные утверждения. Это означает, что логика изучает такие операции над высказываниями, в результате применения которых снова получается высказывание. При этом вовсе не требуется вникать в смысл высказываний, над которыми производятся операции. Математическая логика предлагает формализованный язык для описания этих операций, что позволяет построить формальную модель человеческих рассуждений.

С некоторыми логическими операциями вы наверняка знакомы еще по базовому курсу информатики. Это прежде всего операция конъюнкции (по-другому, операция и), дизъюнкции (по-другому, операция или) и операция отрицания (по-другому, операция не). Но есть и другие операции, они перечислены в табл. 5.1.

Таблица 5.1

В названиях и обозначениях логических операций, приведенных в табл. 5.1, на первом месте указаны те, которые будут использоваться нами. В другой литературе по математической логике употребляются и другие из указанных названий и обозначений.

Во всех логических операциях, кроме операции отрицания, участвуют два аргумента. Поэтому применение, например, конъюнкции к высказываниям X и Y обычно записывают как X & Y, а применение импликации к тем же высказываниям как X Y. Отрицание высказывания X записывают в виде .

Значения логических операций задаются с помощью так называемых таблиц истинности. В них для всевозможных комбинаций значений аргументов записывается результат применения операции. Для всех операций одновременно эти таблицы собраны в табл. 5.2; в ней значения аргументов и результат применения операции обозначены буквами И (истина) и Л (ложь).

Таблица 5.2

Как видно из таблицы, истинность высказывания, полученного применением дизъюнкции, имеет место, когда истинно либо одно высказывание, либо другое, либо оба одновременно. К примеру, истинность высказывания “Идет дождь или дует ветер” означает, что на улице имеет место одна из трех ситуаций: идет дождь и нет ветра; нет дождя, но дует ветер; одновременно идет дождь и дует ветер. Поэтому, записывая данную фразу средствами математической логики, естественно представить ее в виде X Y, где X — это высказывание “Идет дождь”, а Y — высказывание “Дует ветер”.

А вот высказывание “Петя сидит на уроке физики или Петя сидит на уроке истории”, когда оба высказывания, из которых оно составлено, истинны, следует признать ложным — не может Петя одновременно быть и на уроке физики, и на уроке истории. Здесь по смыслу применена операция исключающего ИЛИ. Поэтому, переводя эту фразу на язык математической логики, естественно воспользоваться операцией “” и, соответственно, записать X Y, где X — это высказывание “Петя сидит на уроке физики”, а Y — высказывание “Петя сидит на уроке истории”.

Возможно, вас удивила таблица истинности для операции следования. Многим кажется, что утверждение “Если X, то Y” истинно в том и только том случае, когда X и Y одновременно истинны, т.е. совпадает с конъюнкцией этих высказываний. Но давайте подумаем, когда ложно каждое из высказываний X & Y и X ® Y. Легко понять, что конъюнкция X и Y ложна тогда и только тогда, когда ложно хотя бы одно из высказываний X или Y. А ложность высказывания “Если X, то Y” означает, что хотя высказывание Х истинно, высказывание Y ложно. Отсюда и вытекает то формальное определение импликации, которое приведено в табл. 5.2. В частности, высказывание “Если 2 х 2 = 5, то 2 х 2 = 4” истинно. Как, впрочем, истинно и высказывание “Если
2 х 2 = 5, то 2 х 2 = 3”. Нередко отмеченное свойство импликации формулируют так: из истины следует истина, а из лжи — что угодно.

Обычно с помощью логических операций стараются свести любое высказывание к таким высказываниям, в которых уже нельзя выделить другие высказывания. Такие высказывания, никакая часть которых высказыванием не является, называются простыми.

Вопросы и задания

1. Из приведенных ниже предложений выберите высказывания и обоснуйте свой выбор.

а) Выхожу один я на дорогу.

б) Я спросил у ясеня: “Где моя любимая?”

в) Зачем вы, девушки, красивых любите?

г) Если у вас нет собаки, ее не отравит сосед.

д) Давайте восклицать, друг другом восхищаться.

е) Не пой, красавица, при мне ты песен Грузии печальной.

ж) Вот кто-то с горочки спустился.

з) Ничего на свете лучше нету, чем бродить друзьям по белу свету.

и) Умом Россию не понять.

к) Но кто-то камень положил ему в протянутую руку.

2. Для приведенных ниже высказываний укажите, какие из них истинны и какие ложны.

а) Число 3 является делителем любого числа, у которого сумма цифр равна 6.

б) Некоторые млекопитающие не живут на суше.

в) Никто не может объять необъятное.

г) Демосфен утверждал: “В одну реку нельзя войти дважды”.

д) Каждый год есть месяц, в котором 13-е число приходится на пятницу.

3. Для приведенных ниже высказываний попытайтесь указать, какие из них истинны и какие ложны.

а) Натуральных чисел бесконечно много.

б) Если диагональ выпуклого четырехугольника разбивает его на два равных треугольника, то этот четырехугольник параллелограмм.

в) Серединный перпендикуляр к отрезку — это множество точек, равноудаленных от концов данного отрезка.

г) В десятичной записи числа p встречается 100 раз подряд цифра 9.

д) В записи числа 1/7 в виде бесконечной десятичной дроби не встречается цифра 9.

е) Каждое натуральное число либо простое, либо произведение простых чисел.

ж) Для всех действительных значений х выполнено неравенство  .

з) Для всех действительных значений х выполнено неравенство .

и) Любое натуральное число, у которого сумма цифр равна 2, не делится на 7.

Для всех ли высказываний вам удалось выполнить задание? Почему тем не менее можно утверждать, что все приведенные в пунктах а) — и) предложения являются высказываниями?

4. В приведенных ниже высказываниях выделите два простых, обозначьте их буквами и запишите все высказывания с помощью этих обозначений и логических операций.

а) Петя и Коля идут гулять.

б) Петя идет гулять, а Коля гулять не идет.

в) Если Коля идет гулять, то Петя гулять не идет.

5. Укажите, какую, на ваш взгляд, дизъюнкцию — обычную или разделительную — надо употребить при записи следующих высказываний на языке математической логики.

а) На деревьях распустились листья или раскрылись бутоны.

б) На улице замерз ртутный градусник или от жары пересохла речка.

в) На небе светит Солнце или видна Луна.

6. Определите, какие из приведенных ниже импликаций истинны.

а) Если число 1357 нечетно, то оно делится на 3.

б) Если число 1357 четно, то оно делится на 3.

в) Если число 1357 нечетно, то оно не делится на 3.

г) Если число 1357 делится на 3, то оно нечетно.

д) Если число 1357 не делится на 3, то оно нечетно.

е) Если число 1357 не делится на 3, то оно четно.

7. Составьте таблицы истинности для высказываний

§ 17. Законы алгебры высказываний

В математике алгеброй называется дисциплина, изучающая свойства операций на множествах. Школьная алгебра изучает множество действительных чисел и операции сложения, умножения, вычитания, деления, возведения в степень, которые над этими числами можно выполнять. Некоторые свойства операций известны всем еще по начальной школе, например, переместительный закон сложения: от перемены мест слагаемых сумма не меняется. Справедлив аналогичный закон и для умножения чисел.

Одно из важных изобретений человека, которое легло в основу алгебры, — это введение буквенной символики для записи свойств операций. К примеру, тот же переместительный закон сложения записывается с помощью букв совсем просто: a + b = b + a. Такие равенства, которые верны при любых значениях букв, называются тождествами. По мере изучения алгебры тождеств появлялось все больше и больше, скажем,
(a + b)² = a² + 2ab + b², (ab)ⁿ = aⁿbⁿ и т.д. Прелесть тождеств состоит в том, что, подставляя одни тождества в другие, можно получать новые тождества. Такую процедуру называют тождественными преобразованиями.

Математическая логика, а точнее, тот раздел, о котором мы сейчас рассказываем, имеет дело с множеством высказываний. В предыдущем параграфе мы ввели несколько операций над высказываниями. Следовательно, существует алгебра высказываний — раздел математической логики, изучающий свойства операций над высказываниями. Нас прежде всего будут интересовать те свойства, которые записываются как тождества. Только в нашем случае буквы будут обозначать произвольные высказывания, а знак равенства будет по-прежнему выражать тот факт, что значение левой части равенства совпадает со значением правой части равенства, какие бы высказывания мы в них не подставляли (разумеется, вместо одинаковых букв мы должны подставлять одно и то же высказывание, хотя вовсе не обязательно, чтобы разные буквы заменялись разными высказываниями). В математической логике такие тождественно равные высказывания принято называть равносильными. Сами высказывания, в которых фигурируют буквы, обозначающие произвольные высказывания и соединенные знаками логических операций, называются формулами. Буквы, входящие в такие формулы, называют логическими переменными. Формулы называются тождественно равными или равносильными, если равносильны представленные ими высказывания.

В алгебре действительных чисел доказательство тождеств подчас является довольно трудным делом, требующим определенной изобретательности. В алгебре высказываний доказательство тождества — процесс несложный, хотя и может оказаться весьма трудоемким. Причина здесь в том, что действительных чисел бесконечно много и все не перепробуешь, подставляя их вместо переменных. Что касается алгебры высказываний, то, как вы знаете, значение выражения, составленного с помощью логических операций из других высказываний, зависит только от истинности и ложности входящих в его состав высказываний. Поэтому, составив таблицы истинности для двух таких высказываний, мы можем легко убедиться, равносильны они или нет. 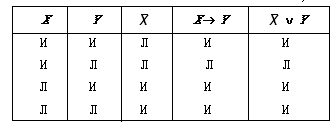Убедимся, к примеру, в равносильности высказываний X Y и XY.

Всем видно, что столбцы для X Y и XY совпали. Значит, можно записать X Y = XY.

Приведем список основных тождеств алгебры высказываний.

Мы выше проверили равенство под номером 20. Остальные равенства можно проверить тем же способом — составить таблицы истинности. Мы оставляем это читателю.

Приведенные выше законы алгебры логики обычно используют для преобразования одних формул в другие, им равносильные. Вот пример (в кружочках над равенствами указаны применяемые законы):

Приведенные 22 тождества вовсе не являются независимыми друг от друга — можно одни из них получать, используя другие тождества того же списка. Вот как, например, выводится закон поглощения (тождество 17) из тождеств 11, 1, 6 и 10:

Закон ассоциативности для операции конъюнкции позволяет не писать скобки, если эта операция применяется подряд к нескольким переменным. Например, вместо можно писать просто X & Y & Z & U & V. Именно так мы и будем делать. Аналогично будем записывать выражения с операцией “”. Если же в записи высказывания встречаются разные операции — отрицание, конъюнкция, дизъюнкция, импликация, — то договоримся, что приоритет их выполнения отдается в указанном порядке: сначала выполняется отрицание, затем конъюнкция, а уже затем дизъюнкция. Если же порядок выполнения операций надо изменить, то применяют скобки. Поэтому выражения (X & Y) (Z & U) и X & Y Z & U совпадают, но отличаются от X & (Y Z) & U. Операции “” и “” имеют самый низкий приоритет.

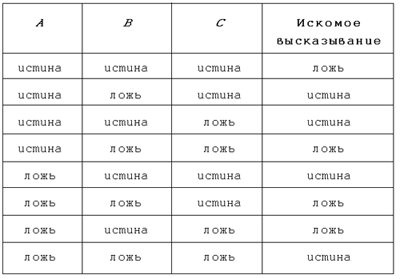
Формула называется тождественно истинной, или тавтологией, если она принимает значение истина при любых значениях входящих в нее переменных. Примером простейшей тавтологии является формула X X.

Из определения операции “” следует, что формулы F₁ и F₂ равносильны тогда и только тогда, когда формула F₁ F₂ является тавтологией.

Подчеркнем еще раз, что математическая логика лишь моделирует логику человеческого рассуждения. К примеру, высказывания X & Y и Y & X математическая логика признает равносильными. И действительно, высказывания “идет дождь и дует ветер” и “дует ветер и идет дождь” в смысловом содержании идентичны друг другу. Но сравните высказывания: “Она вошла в зал, и заиграла музыка”, и “Заиграла музыка, и она вошла в зал”, — и вы почувствуете тонкую, но вполне уловимую разницу, идущую от человеческого восприятия союза “и” как некой упорядоченности событий по времени. Впрочем, в некоторых трансляторах с языков программирования операции дизъюнкции и конъюнкции также не коммутативны (например, в некоторых версиях языка Пролог).

Каким бы ни было сложное высказывание, для него всегда можно составить таблицу истинности. А если дана некоторая таблица истинности, то всегда ли можно записать сложное высказывание, у которого была бы именно такая таблица истинности? Ответ на этот вопрос положителен. Мы покажем на примере, как строить сложное высказывание по таблице истинности, а потом сформулируем общее правило. Пусть, к примеру, таблица истинности выглядит так:

Выберем строки, в которых для искомого высказывания стоит значение истина. Для каждой такой строки вместо значения истина в столбце простого высказывания напишем само высказывание, а вместо значения ложь напишем его отрицание. Получится так:

Таблица 5.5

Теперь в каждой строке соединим получившиеся высказывания конъюнкцией, а полученные таким способом сложные высказывания — дизъюнкцией. У нас получится следующее высказывание:

Конечно, это высказывание можно теперь преобразовывать по указанным ранее законам.

В общем случае надо поступать точно так же:

— оставить в таблице те строки, в которых значение искомого выражения — истина;

— в каждой клетке этих строк записать вместо слова истина само высказывание из заголовка столбца, а вместо слова ложь записать его отрицание;

— соединить конъюнкцией высказывания, стоящие в одной строке, а затем соединить дизъюнкцией получившиеся высказывания для всех отобранных строк.

Обратите внимание, что по этому алгоритму всегда получается формула, в которой используются только операции отрицания, конъюнкции и дизъюнкции, причем так, что отрицание применяется только к переменным, конъюнкцией соединены переменные или их отрицания, причем каждая переменная в таком конъюнктивном выражении фигурирует ровно один раз, и, наконец, дизъюнкции соединяют получившиеся конъюнктивные выражения. Выражение, записанное в таком виде, называется совершенной дизъюнктивной нормальной формой (сокращенно СДНФ). В силу договоренностей о порядке выполнения операций в СДНФ скобки не требуются.

Вопросы и задания

1. Какие высказывания, содержащие переменные, обозначающие высказывания, называются равносильными?

2. Составьте таблицы истинности и выясните, равносильны ли следующие высказывания.

3. а) Составив таблицы истинности, проверьте равенства 1) — 6), приведенные в объяснительном тексте параграфа.

б) Проверьте законы де Моргана, составив соответствующие таблицы истинности.

4. а) Выведите тождество 18 из тождеств с меньшими номерами.

б) Покажите, что законы де Моргана выводятся друг из друга с помощью закона двойного отрицания.

5. Проверьте, что следующие формулы являются тавтологиями.

а) X X;

б) X (Y X).

6. Выясните, какие из следующих формул являются тавтологиями.

7. Выразите высказывание X через высказывания А и В, если имеет место равенство .

8. Выясните, существует ли такая формула F, при подстановке которой в следующую формулу эта формула становится тавтологией.

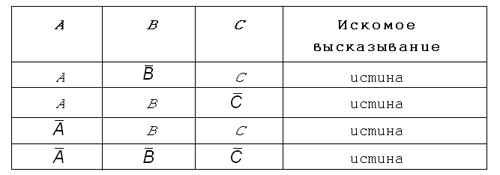
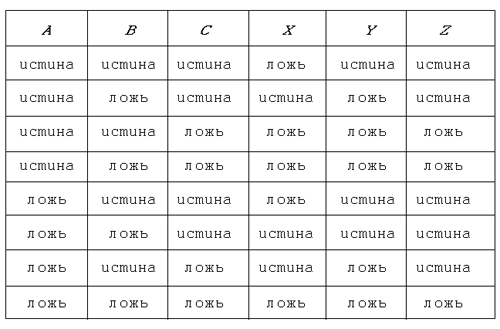
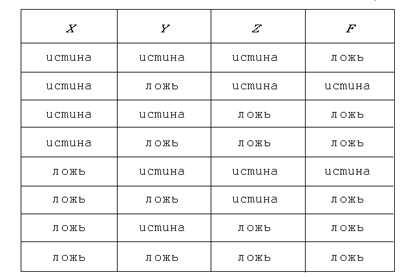
9. а) Запишите через А, В и С высказывания Х, Y и Z, заданные следующей таблицей истинности.

б) Запишите выражения , и преобразуйте их в равносильные выражения, не содержащие скобок.

10. а) Известно, что высказывание F, зависящее от трех высказываний А, В и С, принимает то значение для каждого данного набора значений А, В
и С, которое принимает большинство из этих трех высказываний. Функцию F поэтому называют функцией голосования. Составьте для F логическую формулу.

б) Составьте логическую формулу для функции голосования от четырех переменных.

Контактом (или переключателем) называется устройство, которое в процессе работы может находиться в одном из двух состояний: замкнутом или разомкнутом.

Контакт Х на чертеже будем изображать следующим образом:

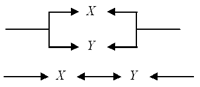
Рис. 1. Изображение контакта

Два контакта X и Y можно соединить между собой различными способами. Вот два из них:

Рис. 2. Параллельное и последовательное соединения контактов

Первое соединение называется параллельным, второе — последовательным. Контакты, соединенные между собой, называют контактной схемой. Будем предполагать наличие у схемы двух выделенных точек — входа и выхода. Схему назовем замкнутой, если существует последовательность замкнутых контактов Х₁, Х₂, ..., Х_n такая, что X_i соединен с Х_i+1, X₁ соединен с входом, Х_n — с выходом. Схему, не являющуюся замкнутой, назовем разомкнутой. Каждому контакту поставим в соответствие высказывание, которое истинно тогда и только тогда, когда контакт замкнут. Высказывание и контакт будем обозначать одной буквой.

Пусть схема S построена из контактов Х₁, Х₂, ..., Х_n с помощью параллельного и последовательного соединений. Тогда по схеме S можно построить формулу логики высказываний FS так, что параллельному соединению соответствует дизъюнкция, последовательному — конъюнкция. Кроме того, действия некоторых контактов могут быть согласованными между собой. Если, к примеру, контакт Y замкнут тогда и только тогда, когда замкнут контакт X, то естественно такие контакты обозначить одной и той же буквой, скажем, X. Если же, наоборот, контакт Y замкнут тогда и только тогда, когда контакт X разомкнут, то контакт Y будем обозначать . На рис. 3 представлена некоторая схема S₀, для которой соответствующая формула выглядит так:

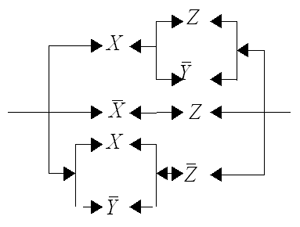
Рис. 3. Контактная схема

Формула F_S “представляет” схему S в следующем смысле: схема S замкнута в том и только в том случае, если Fs принимает значение истина. Нетрудно понять, что по всякой такой формуле F можно восстановить схему, которую формула F представляет.

Пусть схемам S и T соответствуют формулы F_S и F_T в описанном выше смысле. Тогда если схемы S и T эквивалентны (т.е. замкнуты и разомкнуты одновременно), то F_S и F_T равносильны, и обратно. Этот факт используется для решения задачи минимизации контактных схем, которая состоит в том, чтобы по данной схеме S найти схему Т, эквивалентную S и содержащую меньше контактов. Один из путей решения этой задачи состоит в переходе к формуле F_S и в отыскании формулы G, равносильной F_S и содержащей меньше вхождений атомарных формул (разумеется, G построена только с помощью “&”, “” и “^_”, причем отрицание применяется лишь к переменным). Так, например, формула F_S0 равносильна формуле . Следовательно, схема, приведенная на рис. 3, эквивалентна следующей схеме (см. рис. 4), в которой на три контакта меньше.

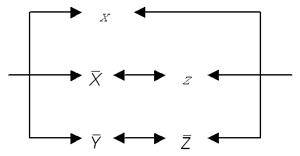
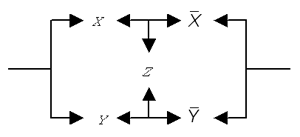
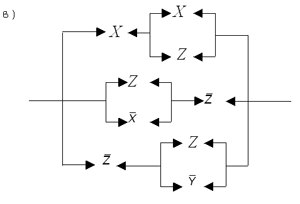
Рис. 4

Скажем откровенно: сегодня еще не придуман алгоритм, позволяющий гарантированно строить схему с минимальным количеством контактов, хотя есть некоторые методы, позволяющие оптимизировать некоторые схемы. Большой вклад в создание таких методов внесли российские ученые Ю.И. Журавлев, С.В. Яблонский и др.

Впрочем, отсутствие такого алгоритма частично объясняется тем, что существуют контактные схемы, в которых параллельные и последовательные соединения осуществляются не столь прямолинейно. Рассмотрим, для примера, такую схему (рис. 5):

Рис. 5. Мостовая схема

Как в этой схеме контакт Z соединен с контактом X? Последовательно или параллельно? Однозначного ответа тут не дать. Между двумя параллельными ветками переброшен мостик. Поэтому и схему такую называют мостовой. Тем не менее для нее нетрудно составить таблицу “истинности”.

По этой таблице уже нетрудно записать формулу для F, а затем построить реализующую ее последовательно-параллельную схему:

Здесь уже потребуется 6 контактов. Впрочем, воспользовавшись дистрибутивным законом, формулу F можно привести к более экономному виду:

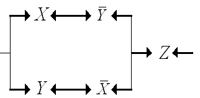
А схема для нее выглядит так:

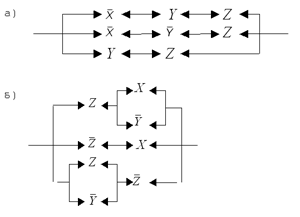
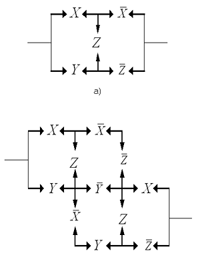
Рис. 6. Последовательно-параллельная схема, эквивалентная мостовой

В данном случае обе схемы получились содержащими один и тот же набор контактов. Но мостовые схемы, как правило, оказываются экономнее последовательно-параллельных.

Вопросы и задания

1. Для следующих цепей построить эквивалентные им более простые цепи:

2. Для каждой мостовой схемы, изображенной на рис. 8, построить эквивалентную ей последовательно-параллельную схему.

Рис. 8

3. Требуется, чтобы включение света в комнате осуществлялось с помощью трех различных переключателей таким образом, чтобы нажатие на любой из них приводило к включению света, если света не было, и выключению света, если тот горел. Построить по возможности наиболее простую переключательную схему, удовлетворяющую этому требованию.

§ 19. Сумматор

В предыдущем параграфе мы отождествили каждый контакт с некоторой переменной. Пусть X и Y — два контакта, или, по-другому, две переменные, каждая из которых способна принимать ровно два значения: 1 или 0. Тогда их параллельное соединение соответствует дизъюнкции этих переменных (по-другому, операции ИЛИ), а последовательное соединение — их конъюнкции (операции И). В табл. 5.8 мы уже в символах 1 и 0 (а не истины и лжи) еще раз описали эти операции.

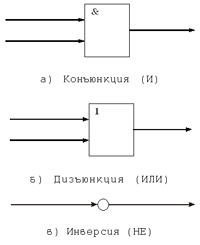
Можно считать, что у нас имеются два устройства, которые выполняют указанные операции. Кроме того, естественно считать, что у нас есть еще операция инверсии — логическое отрицание. Для этих операций имеются даже специальные обозначения (ГОСТ 2.745.91):

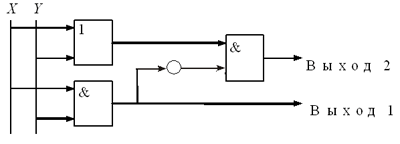
Рис. 9

Принято указанные операции называть вентилями: вентиль И, вентиль ИЛИ, вентиль НЕ.

А теперь из вентилей соберем схему, указанную на рис. 10.

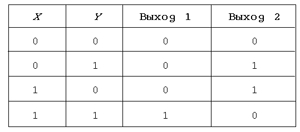
Рис. 10

Чтобы понять, как преобразует входные сигналы X и Y предложенная схема, составим таблицу результатов (см. табл. 5.9).

Сравнивая получившуюся таблицу с таблицей сложения однозначных чисел в двоичной системе счисления, приходим к выводу, что наше устройство на выходах дает два сигнала, которые поразрядно кодируют сумму двух однозначных чисел в двоичной системе счисления. А поскольку действия над числами, записанными в позиционной системе, выполняются поразрядно, то ясно, что аналогичным образом можно построить электронные схемы для сложения многозначных чисел, представленных в двоичной системе счисления. Электронную схему, изображенную на рис. 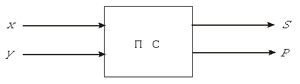10, называют полусумматором. В дальнейшем для краткости полусумматор будем изображать одним блоком (см. рис. 11).
В нем буквой S обозначен младший разряд суммы, а буквой Р — старший разряд или, по-другому, перенос единицы в следующий разряд суммы.

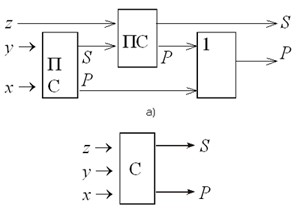
Рис. 11. Полусумматор

При сложении многозначных чисел в старших разрядах приходится учитывать появление так называемой “единицы переноса”. Это означает, что в этих разрядах складываются не два однозначных числа, а три. Используя полусумматор как самостоятельный блок, схему сумматора для сложения чисел в двоичной системе счисления можно изобразить так, как показано на рис. 12. Здесь x и y — единицы разрядов слагаемых, а z — перенос из суммы предыдущих разрядов; выходы S и Р имеют тот же смысл, что и для полусумматора.

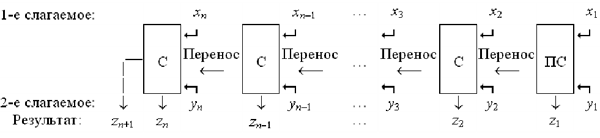
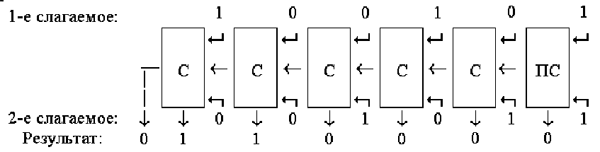
Рис. 12. Схема сумматора (а) и его обозначение
в виде блока (б)

Чтобы сложить два многозначных числа, нужно выстроить батарею сумматоров так, как показано на рис. 13.

А на рис. 14 показана работа такой батареи для чисел 100101 и 1011.

В современном компьютере никто, конечно, не выстраивает подобных батарей. Они входят составной частью в ту или иную микросхему, которая обеспечивает выполнение не только операции сложения, но и целого комплекса операций по обработке двоично закодированной информации.

Вопросы и задания

1. Из вентилей И, ИЛИ, НЕ постройте схему по заданному логическому выражению.

Рис. 13. Батарея сумматоров для сложения двух n-разрядных чисел x_nx_n-1x₃x₂x₁ и y_ny_n-1y₃y₂y₁

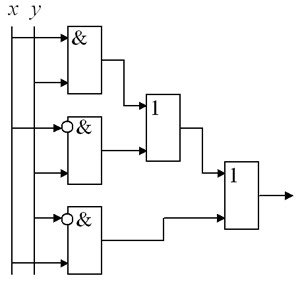
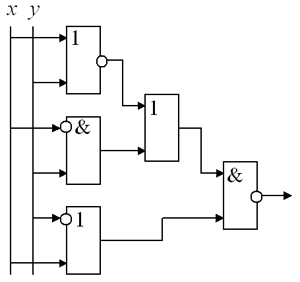
Рис. 14. Сложение чисел 100101 и 1011

2. а) Составьте таблицу значений булевой функции, реализованной схемой, изображенной на рис. 15.

б) Составьте формулу, описывающую схему, изображенную на рис. 15, и попытайтесь ее упростить.

Рис. 15

3. а) Составьте таблицу значений булевой функции, реализованной схемой, изображенной на рис. 16.

б) Составьте формулу, описывающую схему, изображенную на рис. 16, и попытайтесь ее упростить.

Рис. 16